具有食饵群防御和捕食者阶段结构的种群动力学稳定性

张赛楠，申传胜

（安庆师范大学 数理学院，安徽 安庆 246133）

捕食与被捕食是生态系统中普遍存在的自然现象[1-3]。经典的食饵-捕食者Lotka-Volterra 模型中x(t)是食饵种群密度，y(t)是捕食者种群密度，食饵一般遵循Lojistic增长规律，r是食饵内禀增长率，K是环境容纳量，γ是捕食者的死亡率，β是转化率，f(x)是反应食饵与捕食者之间相互作用的功能性反应函数。为描述不同等级物种之间的复杂捕食关系，Holling等提出了经典的Holling I型、II型、III型和IV型等功能性反应函数，其中Holling II型较为合理地反映了中等水平物种之间的捕食关系，因此，该函数应用相对广泛[4-8]。Abadi 研究了一类具有Holling II 型功能性反应函数的Lotka-Volterra模型，结果表明捕食者死亡率低于临界值有利于食饵、捕食者种群持续生存[7]；Kar在Holling II型功能性反应函数条件下，引入食饵避难所机制，推导了系统稳定和物种持久共存的条件[8]。Braza将Lotka-Volterra模型中的功能性反应函数修改为与食饵密度的平方根成正比的函数形式，发现当捕食者死亡率减小到临界值时，系统零平衡点变为稳定的全局吸引态[9]。Panj发展了一类含有食饵群防御和避难所机制的食饵捕食者相互作用的数学模型，并给出了该系统解的正性、有界性以及局部稳定性[10]。然而，文献[9]和[10]直接将捕食者的平均处理时间近似为零，忽略了实际相互作用过程。幼年捕食者一般不具有捕食能力，只有长大到成年才能够捕食和繁殖。因此，捕食者的阶段结构被引入到数学模型之中[11-14]。周学勇等提出了一类具有Crowley-Martin型功能性反应函数和捕食者阶段结构的食饵-捕食者模型，解析得到了正解全局稳定的充分条件[13]；Khajanchi研究了一类具有Monod-Haldane型功能性反应函数和捕食者阶段结构的食饵捕食者模型，发现幼年捕食者的成长率对食饵-捕食者系统动力学行为具有重要影响[14]。

实际上，在真实的生态系统中，食饵的群防御行为和捕食者的阶段特征都是普遍存在的自然现象。为更好地描述食饵群防御和捕食者阶段结构对系统的共同作用效果，本文构建了一类具有食饵群防御和捕食者结构的动力学微分方程模型，并对模型进行分析和数值模拟。

1 数学模型

传统的两种群食饵-捕食者模型为

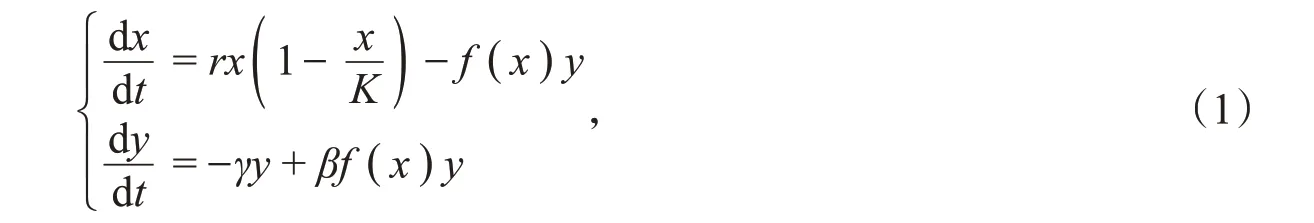
其中，x，y分别表示食饵和捕食者的种群密度；r是x的内禀增长率；K是环境容纳量；f(x)=αx/(1+αx)是Holling II型功能性反应函数，α是y寻找x的搜索效率；β是转换率，γ是y的死亡率。

其中，y1，y2分别是幼年和成年捕食者的密度，γ1和θ分别是y1的死亡率和y1到y2的成长率；γ2是y2的死亡率。从生态学的角度看，系统（2）中所有参数均为正值。

为了清楚地讨论系统（2）中参数对食饵-捕食者模型动力学的影响，在系统（2）中引入无量纲变换：

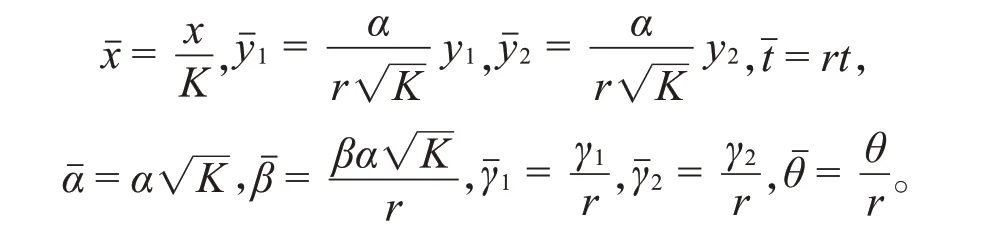
于是，去掉横线，系统（2）转化为下列模型：

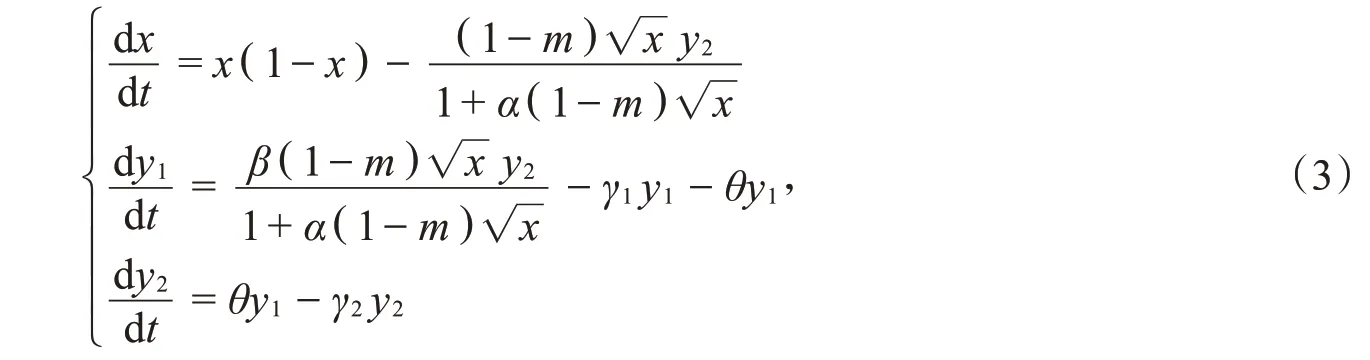
系统（3）中参数的生物意义与系统（2）对应参数的生物意义相同。系统（3）的初始条件为

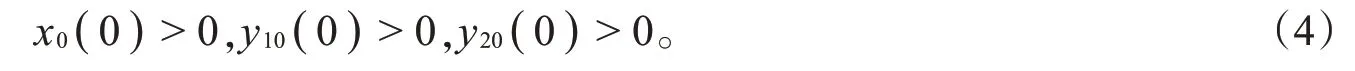
2 解的正性和有界性

定理1系统（3）满足初始条件（4）的解均非负。

证明对于任意t＞0，系统（3）满足初始条件（4）的解为

综上所述，系统（3）满足初始条件（4）的解均非负。

定理2系统（3）满足初始条件（4）的解均有界。

证明构造函数W=x+，有

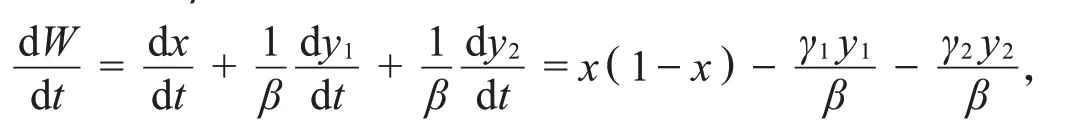
引入一个正数ξ，使得

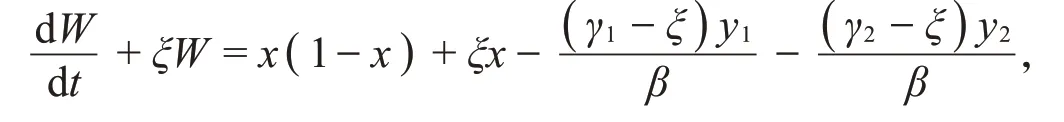
其中ξ=min{γ1,γ2}。然后得到

令g(x)=x( 1+ξ-x)，显然g(x)≤。（5）式可以改写成

解式（6）得

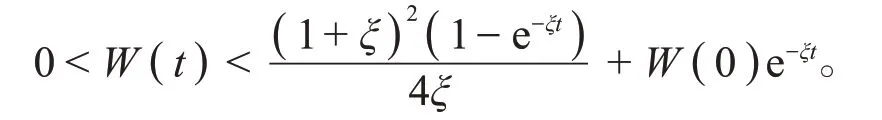
当t→∞时，有0 ＜W(t)＜，即系统（3）满足初始条件（4）的解均有界。

3 平衡点的分析

下面分别讨论系统（3）平衡点的存在性、局部稳定性，以及共存平衡点处发生Hopf分岔的条件。

3.1 平衡点的存在性

当系统（3）达到稳态时，即

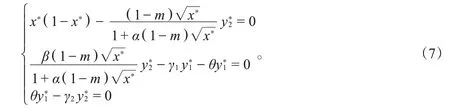
从生态学意义上理解，式（7）有两类平衡点，一类是只有食饵种群存活，而捕食者种群灭绝，此时对应系统（3）的轴向平衡点E1=( 1,0,0)。另一类是食饵和捕食者共存，记共存平衡点为。显然，当

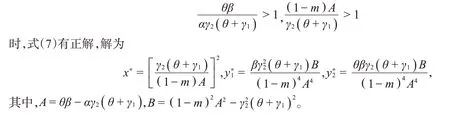
3.2 局部稳定性分析

通过计算系统（3）中平衡点对应雅可比矩阵的特征值来判断平衡点的局部稳定性。

（i）E1处的雅可比矩阵为

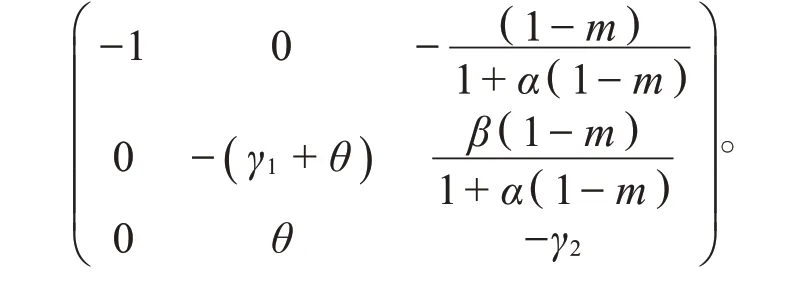
设E1处的特征根分别为λ1、λ2、λ3，则有

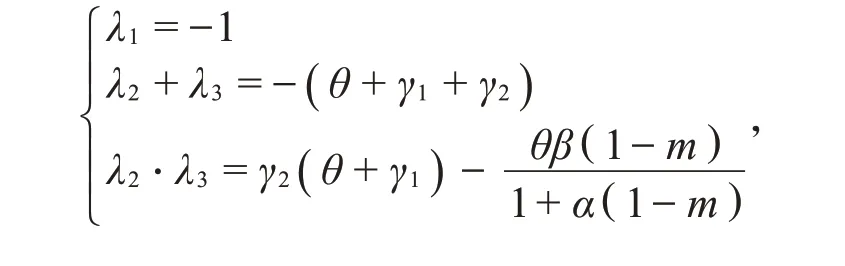
显然，λ1＜0。若

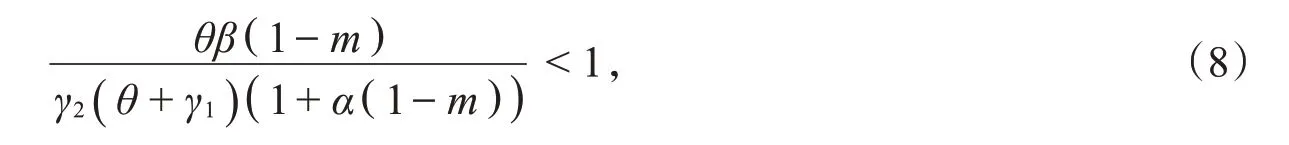
即λ2＜0，λ3＜0，则E1是局部渐近稳定的。若式（8）不成立，则E1是鞍点。

（ii）E2=处的雅可比矩阵为

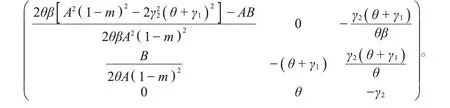
设E2处的特征根分别为λ1、λ2、λ3，特征根满足特征方程为

其中

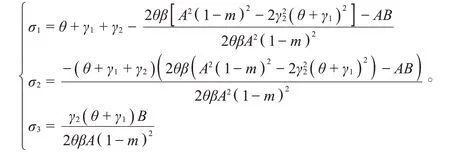
记Δ1=σ1，Δ2=σ1σ2-σ3，Δ3=σ3Δ2。如果

成立，那么根据Routh-Hurwitz判据准则，E2是局部渐近稳定的。

3.3 Hopf分岔

以成年捕食者搜寻食物的效率α和幼年捕食者的成长率θ为分岔参数，讨论在E2处出现Hopf分岔的条件。若σ1σ2-σ3=0，式（9）可写为

4 数值模拟

下面通过数值模拟验证系统平衡点的存在性和稳定性，并研究成年捕食者搜寻食物的效率α和幼年捕食者的成长率θ对食饵-捕食系统动力学行为的影响。选取时间步长dt=0.001，相图曲线的初值分别为( 0.1,0.1,0.1)，( 0.1,0.3,0.1)和( 0.1,0.1,0.3)，分岔图的初值为( 0.1,0.1,0.1)，固定参数：m=0.8，β=1，γ1=0.15，γ2=0.1。

首先，固定θ=1，改变α，分别绘制参数α为0.3和0.6时x、y1和y2的相图，如图1所示。当α=0.3时，σ1=1.270 9，σ3=0.0358，Δ2=-0.002 7，此时不满足Routh-Hurwitz判据准则，E2不稳定，x，y1和y2的相图曲线趋向于一个极限环，如图1（a）所示。当α=0.6时，σ1=1.300 8，σ3=0.0331，Δ2=0.049 5，此时满足Routh-Hurwitz 判据准则，E2稳定，相图曲线趋于E2()0.38145,0.20517,2.0517 。图1 表明系统的稳定与否依赖于成年捕食者搜寻食物的效率，当α较大时，系统趋于共存平衡点的概率较大。

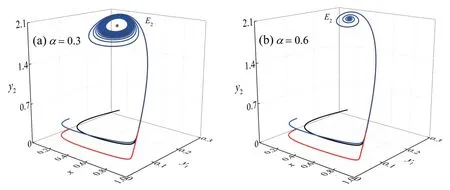
图1 系统（3）在θ=1时的相图。（a）α=0.3；（b）α=0.6

其次，固定α=0.4，改变θ，分别绘制参数θ为0.15，0.8 和1.2 时x、y1和y2的相图，如图2 所示。当θ=0.15 时，参数满足式（8），根据线性稳定性分析，E1为局部渐近稳定，此时x、y1和y2的相图曲线趋于E1( 1,0,0)，如图2（a）所示，表明食饵种群存活，幼年、成年捕食者灭绝。当θ=0.8 时，σ1=1.118 3，σ3=0.027 7，Δ2=0.052 6，参数满足（10）式，根据Routh-Hurwitz判据，E2为局部渐近稳定，此时x、y1和y2的相图曲线趋于E2()0.388 58,0.250 09,2.000 7，如图2（b）所示，表明食饵、幼年和成年捕食者三个种群共存。当θ=1.2 时，σ1=1.4557，σ3=0.042 1，Δ2=-0.030 1，参数不满足式（10），根据Routh-Hurwitz 判据，E2不稳定，此时x、y1和y2的相图曲线趋于一个极限环，如图2（c）所示，表明食饵、幼年和成年捕食者三种群共存时种群密度在一定范围内波动。比较三图可知，幼年捕食者的成长率对食饵-捕食者系统的物种共存与灭绝起到至关重要的作用。数值模拟结果与理论分析一致。

图2 系统（3）在α=0.4时的相图。（a）θ=0.15；（b）θ=0.8；（c）θ=1.2

为了揭示图1的转换机制，我们选择α作为分岔参数，分别绘制x、y1和y2的分岔图，如图3所示。图3（a）表明，随着α增大，系统经历从不稳定状态到Hopf分岔。当α＞αH时，共存平衡点E2局部渐近稳定。由图3（b）和（c）可以看出，y1，y2经历的状态与x相似。当θ=1.2时，x、y1和y2经历状态与θ=1时三者经历状态相似，如图3（d）、（e）、（f）所示，但是系统分岔时的阈值αH变大了，且系统稳定时x、y1和y2的增加速率减小了。图3表明成年捕食者搜寻食物的效率对维持生态系统的稳定性有着十分重要的意义。

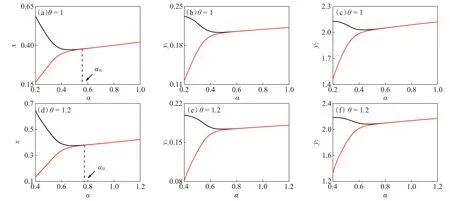
图3 食饵种群和捕食者种群关于参数α的分岔图。（a）、（b）、（c），θ=1；（d）、（e）、（f），θ=1.2

为了揭示图2的转换机制，我们选择θ作为分岔参数，分别绘制x、y1和y2的分岔图，如图4所示，其中图（a）、（b）、（c）为α=0.4，图（d）、（e）、（f）为α=0.8。图4（a）表明，随着θ增大，系统经历从稳定状态到Hopf分岔状态。当θ＞θH时，系统不稳定。由图4（b）和（c）可以看出，y1，y2经历的状态与x相似。当α=0.8时，x、y1和y2经历状态与参数α=0.4时三者经历状态相似，如图4（d）、（e）、（f）所示，但是系统分岔时的阈值θH变大了，且θ＞θH时系统振幅增加。由图4发现，当食饵与捕食者均存活时，适当的幼年捕食者成长率有利于提高成年捕食者搜寻食物的效率。

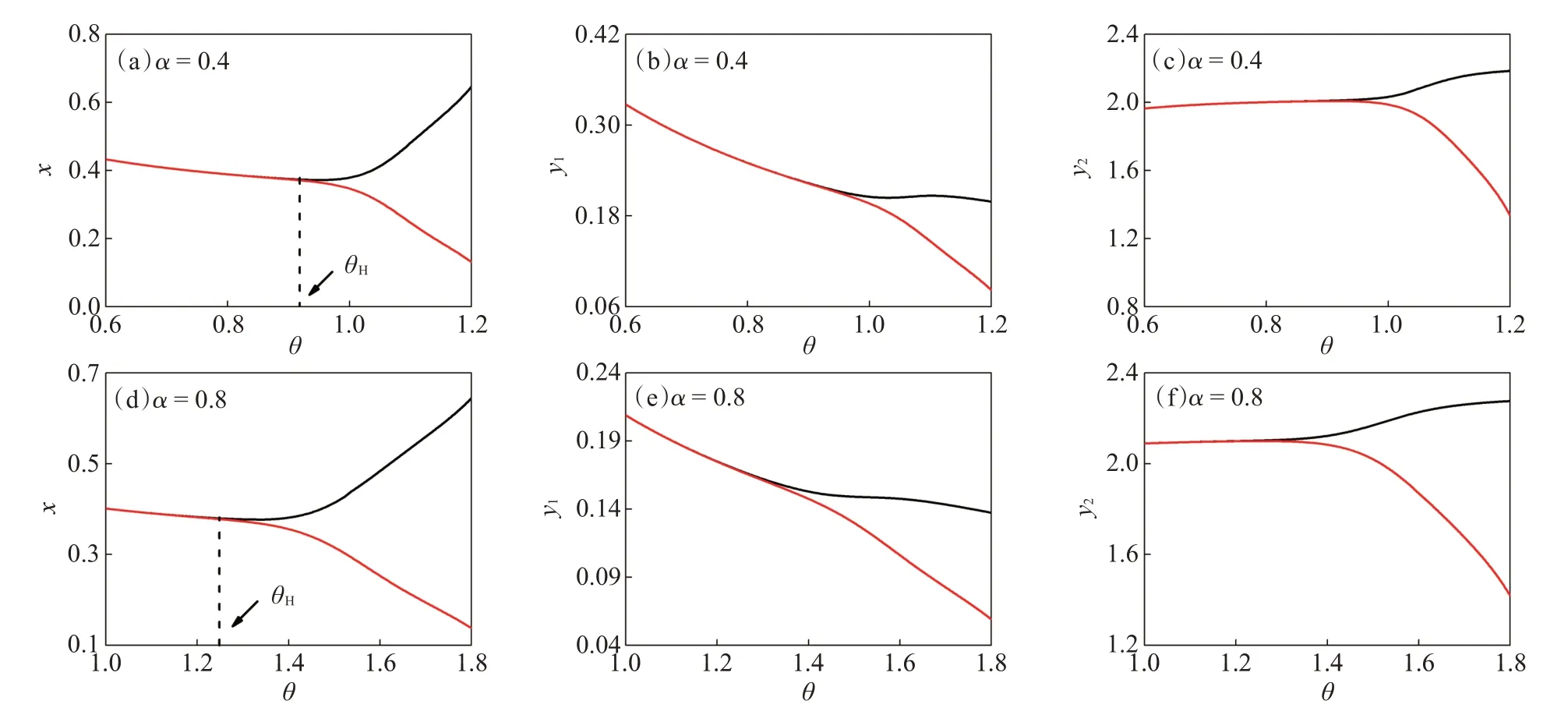
图4 食饵种群和捕食者种群关于参数θ的分岔图。（a）、（b）、（c），α=0.4；（d）、（e）、（f），α=0.8

5 结论

综上所述，我们建立了一类具有食饵群防御行为和捕食者阶段结构的动力学微分方程模型，其中食饵群防御可影响成年捕食者搜寻食物的效率α，捕食者阶段结构将捕食者分为成年和幼年，成年捕食者具有捕食和繁殖能力，幼年捕食者不能捕食和繁殖，但以一定的速率θ长大为成年。本文对模型进行定性分析，证明了系统解正性和有界性，分析了平衡点的存在性，通过计算平衡点对应雅可比矩阵的特征值，讨论平衡点的局部稳定性，并对参数α和θ进行Hopf分岔分析。数值模拟结果发现，成年捕食者搜寻食物的效率α和幼年捕食者的成长率θ诱导出现极限环、稳定点及Hopf分岔等复杂的动力学现象。我们分别计算了系统关于参数α和θ的分岔图，验证了理论分析结果，进一步揭示了不同状态的转换机制。研究表明，食饵群防御和捕食者阶段结构对生态系统动力学稳定性有着十分重要的意义。