两个Sarmanov相依随机变量关于S (γ)族的乘积封闭性
杨月丽,高 宇
(安徽大学 数学科学学院,安徽 合肥 230601)
卷积等价分布族S (γ)是应用概率论中一类重要的分布族,该分布族具有良好的分析性质,广泛应用于分支过程[1]、排队论[2]和风险理论[3]等领域。分布族关于乘积运算封闭性是研究分布族的一个基本问题。乘积结构也是众多应用概率论的基本结构,如它广泛存在于金融保险模型或时间序列ARCH模型[4]中。分布族关于乘积运算的封闭性研究由来已久,文献[5]较早地研究了两个独立的随机变量关于次指数族的乘积封闭性;文献[6]在独立的条件下得到乘积分布属于L(γ)族的若干充分条件;文献[7]得到了两个独立的随机变量关于S (γ)族的乘积封闭性。本文关注了两个相依随机变量关于S (γ)族的乘积封闭性。
文献[8]假设随机向量()X,Y服从二维Sarmanov分布,为证明XY分布属于S (γ)族,用到如下两个技术性假设:
(i)存在一个函数ψ()·,使得对任意的y∈DY,

一般地,上述可测函数ψ()· 与常数c的存在性并不容易获得。即使考虑二维Farlie-Gumbel-Morgenstern分布[9],经计算可得,ψ(y)=1-2G(y),为使存在常数c>0满足条件(ii),则易解得-1/d1<θ<1/d1,表明文献[8]也只获得了二维Sarmanov分布情形下参数属于一定区间的乘积分布是属于卷积等价分布族的充分条件。
鉴于此,本文将采用不同的研究方法,继续研究两个Sarmanov 相依随机变量关于卷积等价分布族的乘积封闭性。
1 定义及引理
假设所有的随机变量均定义在概率空间(Ω,F,P)上,若无特殊申明,均假设随机变量X,Y是非负的,分布函数分别为F(x)=P(X≤x),G(y)=P(Y≤y),其尾分布记为Fˉ(x)=P(X>x),Gˉ(y)=P(Y>y),记XY的分布为H。对于任意两个正函数f(·)与g(·)满足

若b=0,记作f(·)=o(g(·));若a=b=1,记作f(·)~g(·);若b<∞,记作f(·)=O(g(·));若a≥1,记作f(·)≳g(·);若b≤1,记作f(·)≲g(·)。
定义1[10]称分布F属于L(γ)(γ≥0)族,记作F∈L(γ),若对任意固定的y≥0,

定义2[10]称分布F属于卷积等价分布族S (γ)(γ≥0),记作F∈S (γ),如果
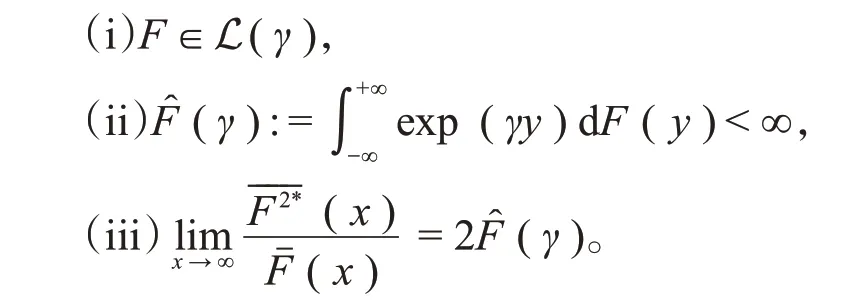
其中,F2*表示分布函数F关于自身的二重卷积。
注1由定义1与2易见:1)S (γ)⊂L(γ)。2)若F∈L(γ)(γ≥0),则(1)对任意y的紧区间一致成立。3)在定义1与2中,若γ=0,则L(0)、S (0)族即为长尾分布族与次指数分布族[10]。
定义3[7]称分布F属于快速变化分布族,记作F∈R-∞,若对任意的y>1,

注2对于任意的γ>0,L(γ)⊂R-∞[7]。
定义4[11]称(X,Y)服从二维Sarmanov分布,若(X,Y)的联合分布满足
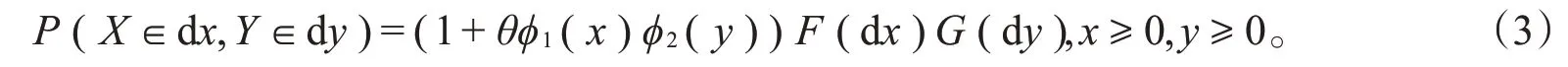
其中,φ1(x),φ2(y)是两个可测函数,参数θ是实常数,满足

其中,DX={x≥0:P(X∈(x-δ,x+δ))>0,对任意的δ>0},
DY={y≥0:P(Y∈(y-δ,y+δ))>0,对任意的δ>0}。
注3特别地,若θ=0或φ1(x)≡0,x∈DX或φ2(y)≡0,y∈DY,则Sarmanov相依退化为独立。
注4在(3)中若取φ1(x)=1-2F(x),φ2(y)=1-2G(y),则Sarmanov分布退化为FGM分布。

将式(8)、(11)、(13)、(14)代入得
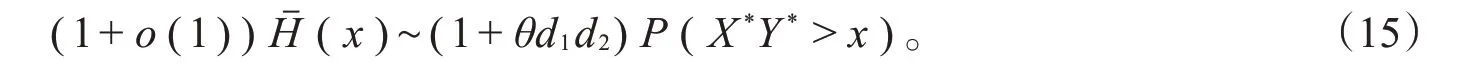
由于X*,Y*是两个独立同分布的随机变量,且与X,Y独立,结合文献[6]有

式(15)和(16)表明

2 主要结果及其证明


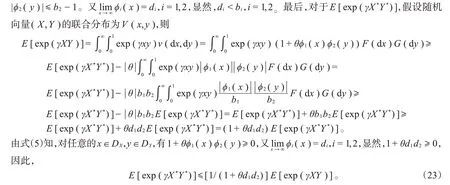
将式(22)、(23)代入式(21)可以得到式(17)成立。因此,定理1成立。
3 结束语
综上所述,本文研究了两个Sarmanov相依随机变量关于S (γ)族的乘积封闭性。在一定条件下,获得了两个Sarmanov 相依随机变量关于卷积等价分布族的乘积封闭性的充分条件,拓展了文献[7]的结果。与文献[8]相比,本文所给的充分条件更易验证;同时,对于二维Sarmanov 分布参数为任意负数情形,本文均获得满意的结果。但遗憾的是,本研究方法在二维Sarmanov分布参数为正数时不适用。

