中原城市群经济高质量发展水平的测度及差异分析

张水利， 李若彤， 王梦羽， 刘东甲

（平顶山学院数学与统计学院，河南平顶山 467000）

1978年改革开放以来，我国经济取得了快速的发展，国内生产总值不断提高，各地区的经济水平也在不断提升. 党的十八届五中全会提出了“高质量发展”这一新的发展理念，所谓高质量发展，不仅指经济增长的高质量，也强调经济发展结果的高质量.

对于经济高质量发展的相关问题，近年来不少学者对此进行了大量研究和探索，例如聂长飞和简新华［1］利用莫兰指数，核密度估计，马尔可夫转移概率矩阵等方法，分析了从2001—2017年中国各个省份高质量水平发展水平及变化趋势；魏敏和李书昊［2］建立了经济结构优化、创新驱动发展、资源配置高效等为子系统的经济高质量发展水平测度体系，并利用熵权TOPSIS法进行了实证测度；师博等［3］从发展的基本面、社会成果和生态成果等三个维度构建了黄河流域经济高质量发展的指标体系，并利用熵值法和均等赋权构成的组合赋权对黄河流域城市经济高质量发展水平进行测度，分析了黄河流域城市的动态研究规律和特征，并对发展趋势进行了预测；刘力钢等［4］利用DEA模型和Dagum基尼系数及其分解方法对东北三省旅游经济增长质量的区域差异及来源进行分析，并研究了区域经济增长质量的动态演进；张乃丽和李宗显［5］采用定基极差熵权法对我国各省份经济发展质量指数进行测算，并利用泰尔指数和核密度估计法分析了中国经济发展质量的地区非均衡特征及动态演进趋势；张曦和郭淑芬［6］采用非导向、非径向、规模报酬可变的窗口MinDS超效率模型对我国30个省份的工业技术创新效率进行测算，同时利用莫兰指数、泰尔指数、核密度估计分析工业技术创新效率的空间相关性、区域差异与动态演进；肖周燕［7］从经济和社会两个方面对中国高质量发展进行分析，研究结果表明，改革开放以来中国发展质量经历了改善—恶化—再改善三个阶段. 近年来，中国正在转变发展方式，优化经济结构，从而推进中国经济高质量发展.

本文以“创新、协调、绿色、开放、共享”五大发展理念为维度，构建了中原城市群经济高质量发展水平评价指标体系，利用熵权TOPSIS模型对中原城市群的30个地区2015—2019年经济高质量发展水平进行测度，并计算泰尔指数并进行分解，对中原城市群各地区进行差异分析，利用马尔科夫链和核密度估计方法，对中原城市群经济高质量发展的动态变化趋势进行了分析.

1 中原城市群经济高质量发展水平的测度

1.1 高质量发展体系指标的建立

本文主要基于“创新、协调、绿色、开放、共享”的新发展理念，来构建高质量发展指标体系. 在选取指标的过程中，遵循以下原则：一是全面覆盖性原则，选取指标要考虑社会发展，生态环境，高质量创新等各方面的问题，使得指标能够较全面反映高质量发展的基本特征；二是指标要有一定的代表性，只有具备较高代表性的指标才会使结果的可信度足够高，才能真正地切合所研究的主题，并且反映出问题的真正结果.

基于上述原则，并结合已有的相关高质量发展指标体系的基础上［8-12］，从创新、协调、绿色、开放、共享五个方面，构建了十三个二级指标，见表1.

表1 中原城市群高质量发展水平测度指标Tab.1 Measurement index of high-quality development level of central plains urban agglomeration

1.2 各地区高质量发展水平指数的数据来源以及测度方法和结果

1.2.1 数据来源

本文数据主要来源于2016—2020年《中国统计年鉴》《河南统计年鉴》《山东统计年鉴》《山西统计年鉴》《河北统计年鉴》《安徽统计年鉴》及各市区国民经济和社会发展统计公报.

1.2.2 测度方法和结果

本文采用熵权TOPSIS模型［13-18］对中原城市群经济高质量发展水平进行测度. 首先计算出发展权重，进一步再计算出相对接近度Ci，即高质量发展指数. 利用熵权TOPSIS模型测度中原城市群经济高质量发展水平指数，主要思路是对每个测量指标数据进行标准化处理，每个测量指标的权重值通过熵给出，之后再根据相关公式和步骤计算出相应的发展指数，具体公式步骤如下所示：

式中：Xij指i个年份j个评价指标，i=1，2，…，n，j=1，2，…，m.

2）计算各测度指标的信息熵值Ej：

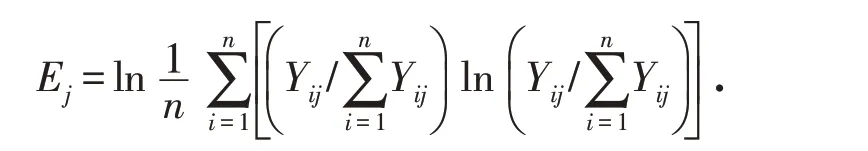
3）计算高质量发展体系中每个测量指标的权重Wj：

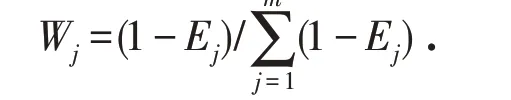
4）构建测量指标的加权矩阵R，并且通过加权矩阵计算来确定最优方案Q+j和最劣方案Q-

j：

5）计算出各测度方案与最优方案和最劣方案的欧氏距离d+i和d-

i：

6）计算每个测度方案与理想方案的相对接近度Ci：

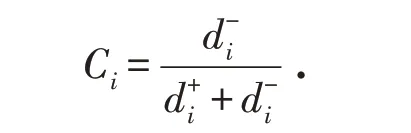
式中：相对接近度Ci定义为发展指数，它是在0到1之间，其值越大表明经济高质量发展水平越好；相反，经济高质量发展水平较差.

根据所得数据，利用熵权TOPSIS分析法计算得出2015—2019年各市高质量发展指数，见表2.

表2 中原城市群2015—2019年各市经济高质量发展水平指数Tab.2 The index of high-quality economic development level for central plains urban agglomeration from 2015 to 2019

1.3 经济高质量发展水平结果分析

根据以上计算得出的中原城市群经济高质量发展水平指数，把中原城市群按照所属省份分为5类，即河南、安徽、山西、河北、山东，并且为了能够更直观地看出中原城市群各个省份及总体经济高质量发展指数的变化趋势，做出对应的折线图，如图1所示.

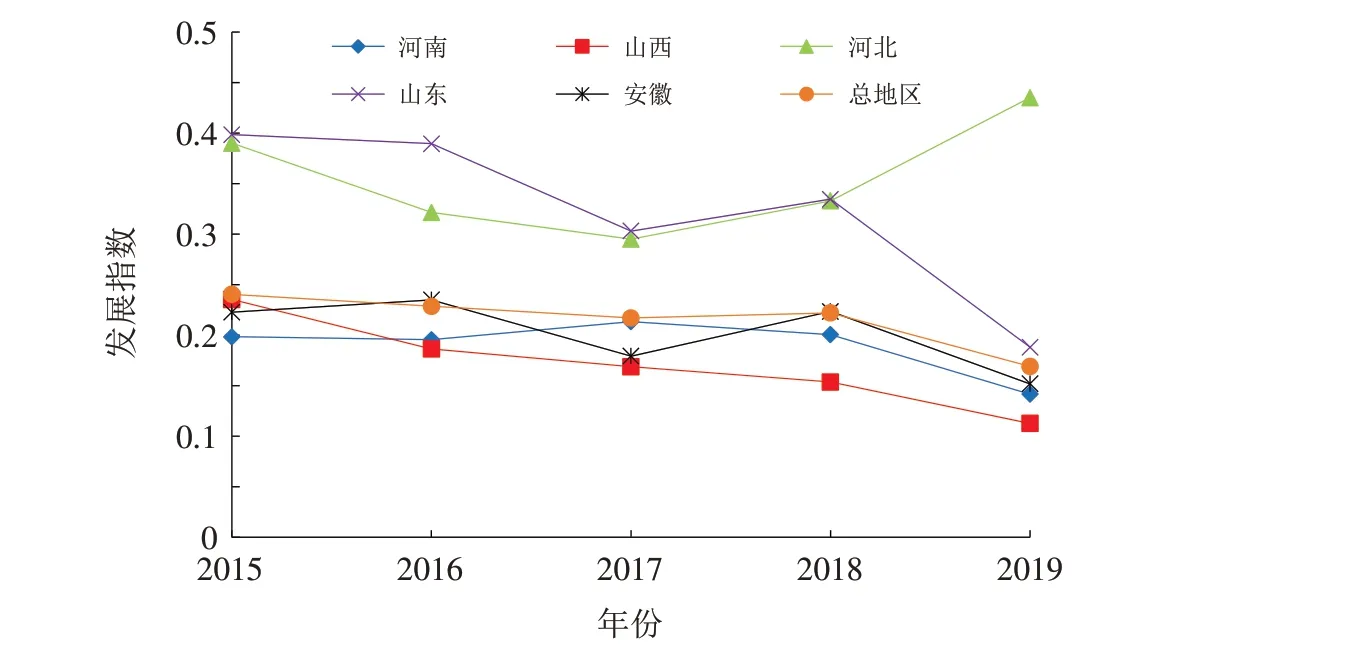
图1 中原城市群各省经济高质量发展综合评价均值变化趋势Fig.1 Change trend of the mean value of comprehensive evaluation of high-quality economic development in each province of central plains urban agglomeration

根据数据分析结果可以看出，中原城市群各省市总体发展水平的波动不大，只有在2019 年出现了较为明显的下降. 而从各个省份的发展及其之间的关系来看，山西省呈现出逐年下降的趋势，且长治、晋城和运城这三市的发展指数在2016 年及之后的几年内的发展都处于中原城市群的低位区；而山东和河北在2015—2018 年期间的发展指数变化相比2019年的变化较为不明显；河南省、安徽省与中原经济区的总体发展指数比较接近，但安徽省在2017年时的下降较为明显，而河南省在2015—2017年是持续上升的，2018年略微出现了下降的趋势.

2 中原城市群经济高质量发展水平差异分析

为了更好地了解中原城市群各地区经济高质量发展指数的差异，借鉴文献［1］中的做法，利用R软件计算出泰尔指数并进行分解，对经济高质量发展的差异性进行分析.

1）泰尔指数的计算方法

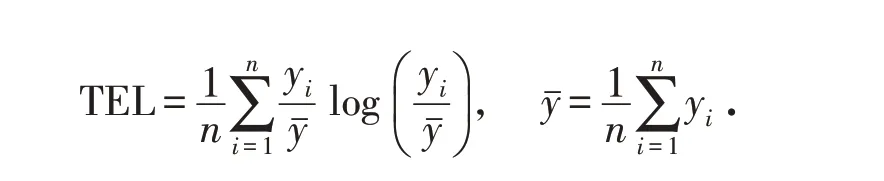
式中：TEL表示泰尔指数，其值介于［0，1］之间，若该区域经济发展在绝对同等的水平上，泰尔指数的值为0；而当地区的经济发展水平差距较大时，泰尔指数的值就会越来越趋近于1.

2）泰尔指数分解法

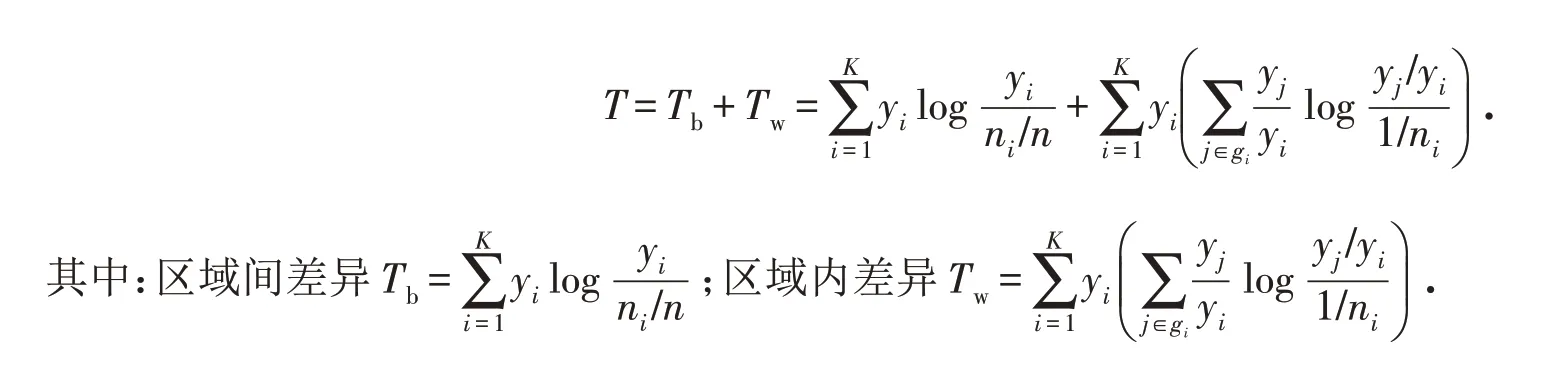
通过泰尔指数及其分解可以将中原城市群的差异更加清楚地呈现出来，更有利于经济发展的分析. 利用R 语言计算2015—2019 年中原城市群经济高质量发展指数的泰尔指数T、区域间差异Tb以及区域内差异Tw，见表3.

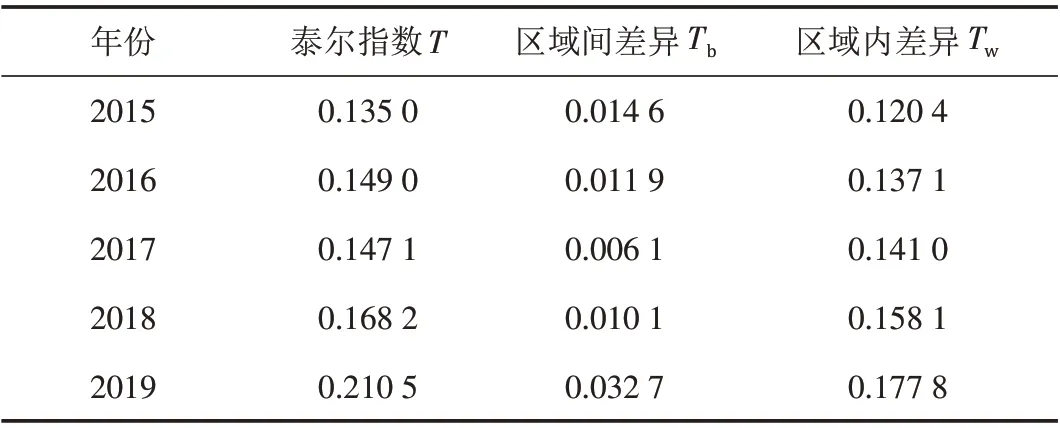
表3 中原城市群经济高质量发展的泰尔指数及其结构分解Tab.3 Theil index and its structural decomposition of high-quality economic development of central plains urban agglomeration

从总体来看，2015—2019 年期间，中原城市群高质量发展指数的泰尔指数呈现上升趋势，从2015 年的最小值0.135 0 增加到2019年的最大值0.210 5，这表明中原城市群高质量发展指数的总体差异有增加趋势. 从结构分解结果看，高质量发展指数的总体差异主要来源于地区内差异，其贡献均在84.5%以上.

3 中原城市群经济高质量发展水平动态分析

3.1 马尔科夫链分析

马尔科夫链（Markov Chain）又称作马氏链，它是一类随机过程，并且具有所谓的“无后效性”. 本文主要运用离散时间的马氏链，通过构建马尔科夫转移概率矩阵，研究中原城市群各地区2015—2019年高质量水平发展水平状态演进过程.

对任意状态i，j，i0，i1，…，in-1，有

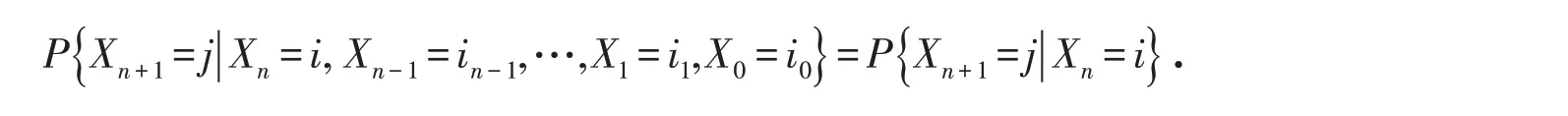
其中：Xn=i表示过程在时刻n处于状态i，称｛0，1，2，…｝为该过程的状态空间，记为S；其中条件概率P{Xn+1=j|Xn=i} 称为马氏链{Xn,n=0,1,2,… }的一步转移概率，简称转移概率，记为Pij，它表示在状态i经过一步转移到状态j的概率.

本文采用四分位数法，将中原城市群的高质量发展指数分为四个等级，分别为低水平Ⅰ、中低水平Ⅱ、中高水平Ⅲ和高水平Ⅳ.由中原城市群高质量发展指数，通过计算可以得到中原城市群高质量发展指数的转移概率矩阵，见表4.

由表4可知：①在转移概率中，对角线上的转移概率均大于非对角线上的概率且都大于50%，其存在“条件收敛”的现象；最小值为51.72%，表明中原城市群高质量发展保持平稳的最小概率为51.72%；处于高水平和低水平的城市保持平稳的概率较大，分别为83.90%，77.27%. 由此可以看出中原城市群的发展存在着富者更富，穷者更穷的“马太效应”. ②低水平、中低水平和中高水平正向发展的概率分别为22.73%、10.35%、3.34%. 由此可见，发展水平越高的城市正向变迁的概率会越小，这也说明，在经济高质量发展的后期想要向正向转变的概率相较于前者会更难. ③非对角线上的概率有些为0，表明有些发展的转变可以认为不可能，即得出经济的高质量发展想要实现跨越式转移的可能性非常小.

表4 马尔科夫转移概率矩阵Tab.4 Markov transition probability matrix

3.2 核密度估计分析

核密度评估是研究数据分布特征的一种重要的非参数估计方法［9］. 该方法对随机变量的密度函数进行估计，使用核密度曲线反映随机变量的位置、形态及延展性.

3.2.1 核密度估计模型

核密度估计是属于非参数检验中的一种重要方法，是一种用来估计未知的密度函数，该方法对数据的分布不需要附加任何假定，设其概率密度函数为f(x)，则该函数可以由下式进行估计.

其中：K表示核函数，该核函数是非负的，如果越接近0，则密度值就越大，符合概率密度的性质；h称为带宽，而带宽的选择会直接影响到估计的结果，当带宽越小时，估计的精确度就会越高.

3.2.2 核密度图及相关分析

根据经济高质量发展指数，利用R软件做出了相应的核密度分析（图2），不同时期核密度估计曲线图代表不同时期的经济高质量发展状态.

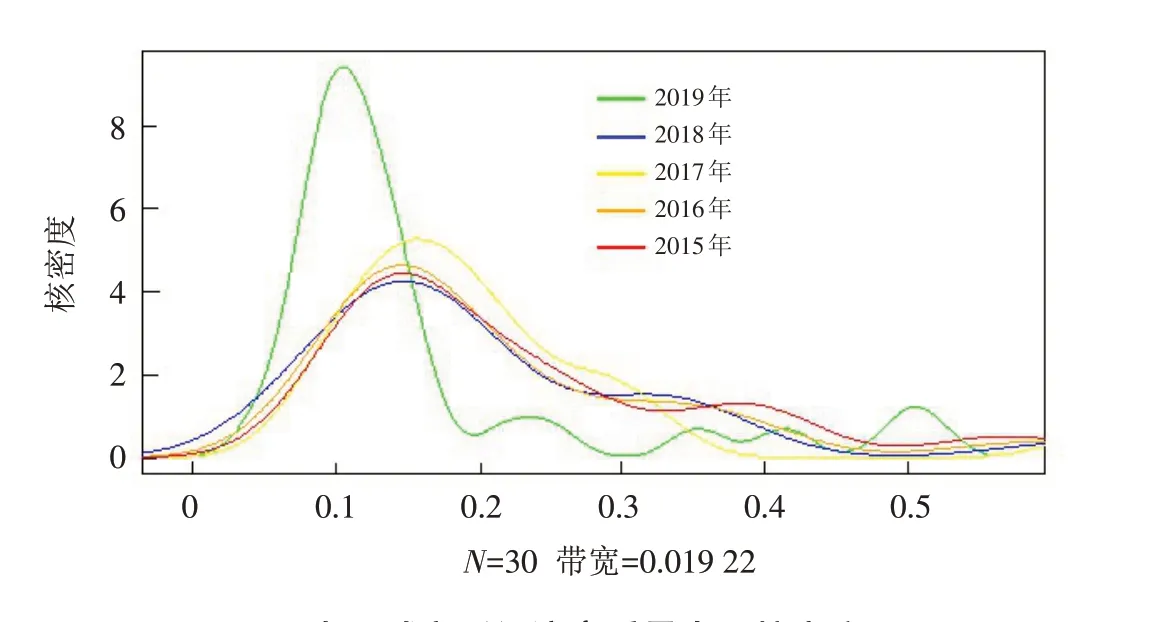
图2 中原城市群经济高质量发展核密度图Fig.2 Kernel density map of high-quality economic development of central plains urban agglomeration

由图2可知，中原城市群各市区经济高质量发展的主要变化是：核密度曲线从2015—2018 年有右移的倾向，这表明各市高质量发展水平是在不断地上升，发展的门槛和极限值也存在不断转好的趋势. 2019年稍许左移，经济发展呈现出略微下降的趋势. 此外每个主峰的峰值也是在不断地变化，可以从三个方面上分析：①从位置上来看，2015—2019年核密度的峰值存在明显的位移，2015年和2016年峰位相近，表明经济发展相对稳定，但在2017—2019年峰值变化趋势较大这表明中原城市群各市高质量发展情况比较聚集；②从形状上来看，2015和2016年的坡度较为缓和，相对的密度值较低，2017—2019年整体的坡度更为陡峭，即密度比较高，表示中原城市群向更高质量的方向聚拢；③从峰度上看，2015—2019年中原城市群高质量发展由宽峰转变为了尖峰，而且在2019年峰顶的密度值相对来说比较高，在0～0.2的区间上更加聚集，并且相对来说峰数较多，表明低值地区在向中值地区发展，并且中值地区在向高值地区演变.

4 结论

本文基于新时代经济高质量的发展，对中原城市群在2015—2019年的经济认识做出了更进一步地分析与研究. 采用熵权TOPSIS模型，利用R软件计算泰尔指数并对其进行分解，以此来分析中原城市群不同地区的经济发展差异情况，利用马尔科夫链模型及核密度估计方法，分析了中原城市群经济高质量发展水平的动态演进过程.

1）不同省份及不同的城市之间的高质量发展存在着不同的趋势与分布特征；郑州和洛阳发展指数相对较高，并且2015—2018年属于逐步递增状态；开封、平顶山、安阳、许昌整体变化趋势不大，处于平稳状态；鹤壁、新乡、济源、晋城整体发展水平略有减少；南阳、商丘、周口发展水平处于逐年上升状态；整体来看，随着时间的变化中原城市群经济高质量发展差距在逐渐减小.

2）从泰尔指数可以看出，近年来各个地区之间的发展差异是相对较小的，而彼此之间存在较强的相关性. 从马尔可夫链动态演进的规律及趋势可以看到，2015—2019 年的发展变化更好地反映了地区间低水平、中低水平、中高水平和高水平之间互相转化的情况，可以更好分析经济发展的变化情况，同时也能够预测未来经济发展的变化情况.

3）从核密度估计分析图中，中原城市群各地区的高质量发展水平和区域间的差异变化情况来看，中原城市群在2015—2018年间其经济高质量发展指数基本呈现出上升的趋势，仅有2019年，因为经济发展的原因，导致其发展指数出现了下降趋势.