基于多标度特征分析及速率比趋势判断的基坑变形规律研究
李晓斌, 薛晓辉,2
(1.陕西铁路工程职业技术学院,陕西渭南 714000;2.河北省岩土工程安全与变形控制重点实验室(河北水利电力学院),河北沧州 061001)
随着市政地铁工程的快速发展,车站基坑数量也越来越多,且为满足车站后续运营要求,基坑位置多处于繁华区,使得其近接建、构筑物日趋复杂,施工过程的变形控制要求较高,因此,开展基坑变形规律研究显得格外重要[1-2]. 目前,已有不少学者开展了此方面研究,如宫志群等[3]、任建喜等[4]利用数值模拟开展了土岩二元地层结构的基坑变形规律研究;马琳[5]则基于基坑变形监测成果,通过变形预测及趋势判断进行了基坑变形规律分析. 上述研究虽在变形规律研究方面取得了一定成果,但其均未涉及基坑变形的多标度特征分析,也未引入速率比的趋势判断研究,因此,仍可基于此两方面进一步拓展基坑变形规律的研究思路. 同时,常瑶[6]的研究成果表明多重分形消除趋势波动分析(Multi-Fractal Detrended Fluctuation Analysis,MF-DFA)可有效评价岩土变形序列的多标度特征;张志会等[7]也验证了速率比概念适用于基坑变形预警评价. 因此,以MF-DFA模型和速率比概念开展基坑变形规律研究是有效的. 综合上述,论文以武汉洪山站地铁基坑为工程背景,先通过MF-DFA 模型和Spearman秩次检验开展基坑变形的多标度特征分析,再在基坑变形速率比计算基础上,进一步利用Spearman秩次检验进行其发展趋势评价,最后结合多标度特征分析结果及速率比趋势判断结果,综合评价基坑变形规律,以期为现场施工奠定一定的理论基础.
1 基本原理
1.1 多标度特征分析模型的构建
MF-DFA模型是一种常用的多重分形方法,其不仅适用于非均匀多重分形评价,还可判断评价指标的发展趋势,因此,提出利用其构建多标度特征分析的基础指标[6,8-10]. 在MF-DFA模型的应用过程中,先对基坑变形数据进行整理,即先计算基坑变形的累计离差序列,再对其进行子序列划分,且子序列长度设置为s,若累计离差序列的总个数为N,那子序列个数可表示为:Ns=N/s. 值得指出的是,Ns并不一定为整数,这样则不能充分发挥所有数据的作用,因此,提出在累计离差序列正向子区间划分基础上,再进行逆序划分,将子序列个数增加至2Ns个,以充分发挥所有累计离差节点的作用.
在子序列划分基础上,设定波动函数的阶次q,并计算此阶次条件下的波动函数F(q,s):

式中:F2(s,v)为方差值;v为子序列序号.
据式(1),当子序列长度s设定时,波动函数F(q,s)值与之具有对应关系,因此,当改变子序列长度s后,亦可得到若干对应的F(q,s)值,即若干散点(s,F(q,s)),且s值与F(q,s)值间存在如下关系:

式中:h(q)为对应q阶条件下的Hurst指数;C为常数,由拟合过程求得. 在分析过程中,将波动函数的阶次q设定为-10~10间的偶数值,并根据h(q)值的变化来判断基坑变形数据的多重分形特征,具体判据为:若q值变化时,h(q)值也随之变化,那么此基坑变形序列即具有多重分形特征;反之,则不具有多重分形特征.
同时,以h(2)值为指标,可初步判断基坑变形的发展趋势,判据如下:
1)若h(2)值在(0.5 1.0)区间时,基坑变形持正向增加趋势,且h(2)值越趋近于1,趋势性越强.
2)若h(2)值等于0.5时,基坑变形属游离状态,其发展趋势无法判断.
3)若h(2)值在[0 0.5)区间时,基坑变形持反向下降趋势,且h(2)值越趋近于0,趋势性越强.
最后,以q值与h(q)值为基础,进一步计算奇异指数a(q):

式中:h′(q)为h(q)的对应导函数值. 通过奇异指数a(q)进一步计算多重分形谱宽度参数Δa和波形中大小波动所占比例参数Δf(a):

式中:amax、amin为奇异指数的最大值和最小值. ①Δa参数可评价基坑变形的多重分形谱宽度,且Δa值越大,则多重分形宽度也相对越强,即波动会越剧烈;②Δf(a)参数可评价基坑变形中各类大小波动的所占比例,且Δf(a)值越大,大波动波形的所占比例越小.
为充分掌握基坑变形的多重分形谱宽度及各类大小波动的所占比例,需再构建多重分形谱宽度参数Δa和波形中大小波动所占比例参数Δf(a)的趋势判断模型. 考虑到Spearman秩次检验在小样本数据中具有广泛的适用性[11-14],因此,利用其实现Δa参数和Δf(a)参数的趋势判断是可行的.
在Spearman秩次检验的应用过程中,将评价指标的变化序列表示为{X1,X2,…,Xn},按值的大小,进行重新排序,并得到新的序列{Y1,Y2,…,Yn},以此两序列进行秩系数rs求解,即:

式中:n为序列节点总数. 根据rs值即可判断对应评价参数的发展趋势,即当rs>0 时,得评价指标具上升趋势;反之,评价指标具下降趋势. 同时,当rs的绝对值大于对应显著性水平a条件下的临界值Wa时,可认为其趋势性更加显著,因此,可依据此对评价指标的趋势性等级进行划分,具体标准如表1所示.
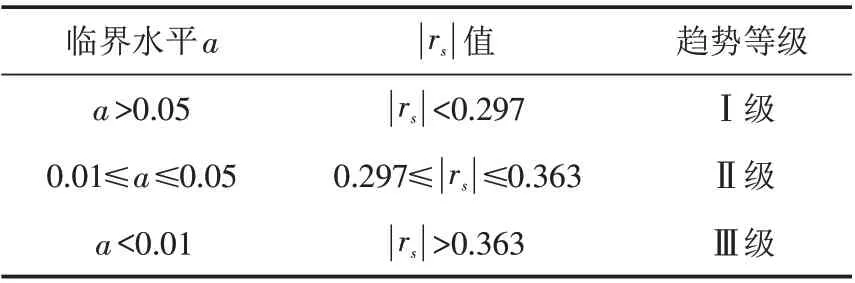
表1 趋势等级划分标准Tab.1 Criteria for trend classification
1.2 速率比趋势判断模型的构建
为综合掌握基坑变形规律,在前述基坑变形多标度特征分析特征基础上,再引入速率比概念,进一步开展基坑变形趋势评价. 值得指出的是,速率比指标不仅能反映每个监测点或每类监测项目的变形情况,还能对不同监测点间的变形特征进行对比.根据相关文献[15-16]的研究成果,速率比指标ε的计算公式为:

式中:vt为对应时间节点处的变形速率;v′为变形速率的均值;t为时间变量.
据式(7),上述两参数都可基于现场监测成果统计得到,可操作性较强,并可根据速率比指标ε进行变形阶段划分,具体如下:
1)当ε<1时,说明基坑变形处于减速变形阶段,即基坑变形后期趋于稳定.
2)当1≤ε<2时,说明基坑变形处于等速变形阶段,即基坑变形趋于增加趋势,但增加速率相对一般.
3)当ε≥2时,说明基坑变形处于加速变形阶段,即基坑变形趋于增加趋势,且增加速率较大.
同时,按照论文分析思路,需再对速率比的发展趋势进行评价,且考虑到前述Spearman秩次检验具有良好的趋势判断结果,因此,也利用其实现速率比的趋势判断,以掌握基坑变形的趋势性特征.
2 实例分析
2.1 工程概况
洪山站隶属于武汉八号线二期工程,车站设计为地下两层岛式车站,起止里程为CK22+145.85 m~CK22+387.65 m,中心里程为CK22+280.00 m;同时,车站外包长度为241.8 m,站台有效长度186 m,标准段宽度为21.30 m,中心顶板的覆土层厚度为4.57 m[17-20]. 据现场调查,洪山站位于洪山路与东一路的十字路口处,近似呈南北延伸,其东北侧为8~11 层建筑;西北侧为低矮民宅;西南、东南侧均为8~11 层监测,且此路段的车流量巨大,加之地下管线复杂,给施工带来了巨大难度.
根据现场钻探成果,区内第四系地层主要以填土、粉质黏土为主,其中,填土包括杂填土、素填土,颜色混杂,潮湿~饱和状态,层厚分布较连续,但厚度差异较大,主要分布于地表浅层;粉质黏土在区内广泛分布,灰黄色为主,可塑~硬塑状态,压缩性中等~高,局部含有一定量的碎石. 基岩主要以砂质泥岩、石英砂岩为主,前者灰黄色、灰绿色,节理风化严重,完整性较差,且岩质较软;后者灰白色、灰黄色,具砂质结构,层状构造,节理裂隙一般发育,完整性一般.
在水文条件方面,区内地表水较发育,地下水以孔隙水和上层滞水为主,其中,孔隙水赋存于砾石层中,所在里程主要为:CK22+300 m~CK23+300 m,分布较连续,水力联系较好;上层滞水多赋存于人工填土层中,无统一自由水面,埋深为1.9~3.9 m. 两者主要接受大气降雨或地下水补给.
在施工过程中,为及时掌握基坑周边地层、支护系统的工作状态,对现场进行了变形监测,如周边地层沉降监测(编号:DB)、侧位移监测(编号:CX)及桩顶竖向变形监测(编号:GL)等,三者均属于必测项目,因此,提出以此三类监测项目为例开展基坑变形规律研究. 考虑到篇幅原因,选取基坑中心位置断面进行分析,其中,地层沉降监测点为DB8和DB24监测点;侧位移监测点为CX10和CX11监测点;桩顶竖向变形监测点为GL10和GL11监测点.
结合监测成果,将基坑变形统计周期设置为5 d/期,并得到各监测点的最终变形量如图1 所示. 从图1可见,各类监测项目的累计变形量存在一定差异,其中,地表沉降变形量与侧位移变形量相近,侧位移量相对略大;桩顶竖向变形量均明显小于前两者,变形值主要间于7.35~7.49 mm.

图1 各检测点基坑变形位移值Fig.1 Deformation displacement values of foundation pit of each monitoring point
2.2 基坑变形的多标度特征分析
按照论文思路,本节重点开展基坑变形的多标度特征分析,且为实现其分析效果的综合评价,将此过程划分为两个步骤:其一,先通过MF-DFA模型开展基坑变形的现状多标度特征分析;其二,在前者分析基础上,再进一步利用Spearman秩次检验开展多标度特征的发展趋势评价.
首先,对不同波动阶次q条件下的波动函数值进行计算统计,得表2. 从表2 可知,在相应阶次q条件下,各监测点的h(q)值存在一定差异,且在相应监测点条件下,当q值增加时,h(q)值也随之变小,说明各类基坑变形是具有多重分形特征的,但其分形特征存在一定不同. 同时,对比各类监测项目的h(2)值,得6个监测点的h(2)值均大于0.5,说明各类监测项目持正向增加趋势,但6个监测点的h(2)值是存在一定差异的,其中,CX10和CX11监测点的h(2)值相对最大,其次是地表沉降监测点和桩顶竖向变形监测点,即进一步说明在基坑变形中各变形趋势性为:地层沉降变形>侧位移变形>桩顶竖向变形.
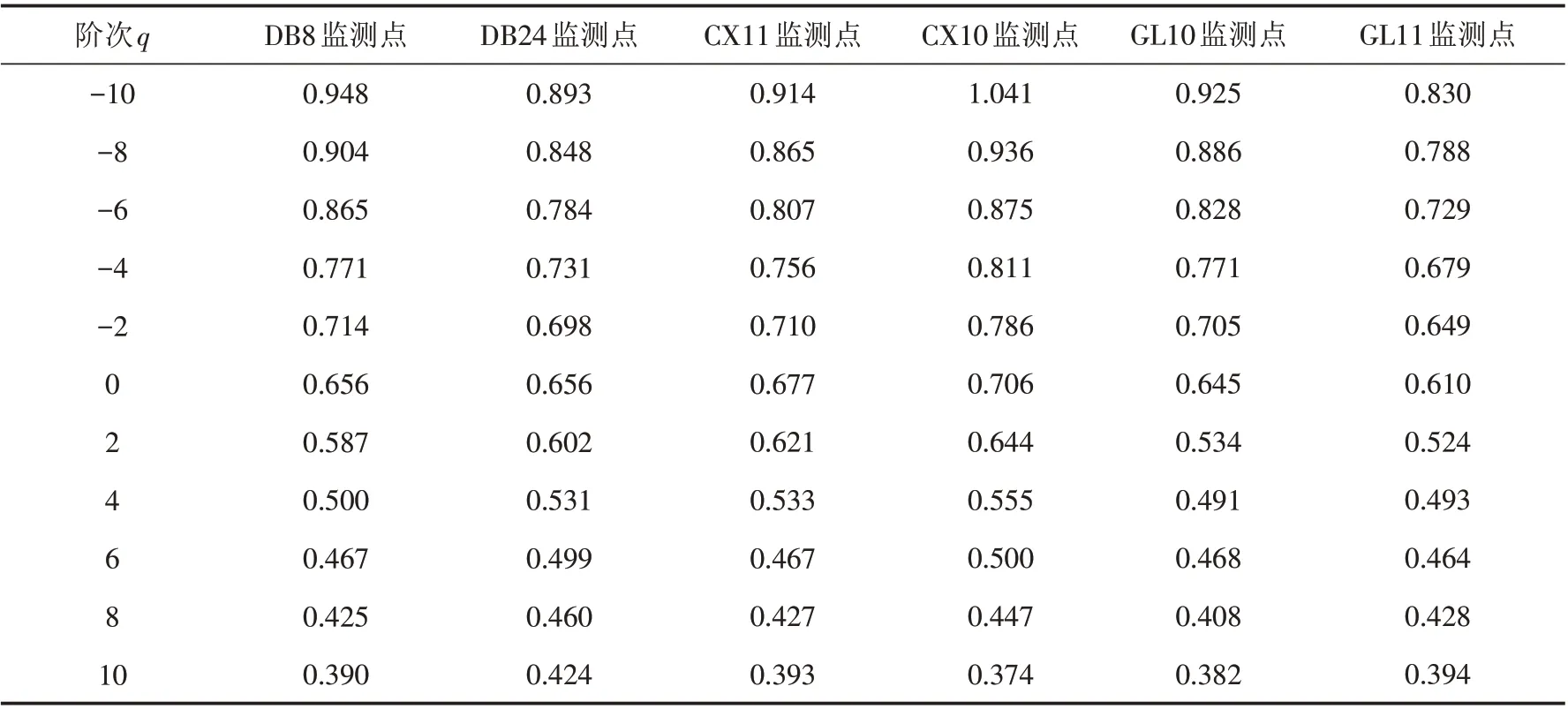
表2 各监测点的多重分形特征结果Tab.2 Multifractal characteristic results of each monitoring point
其次,再对Δa参数和Δf(a)参数的现状值进行求解,以评价基坑变形的多重分形谱宽度及各类大小波动的所占比例,经计算统计,得其结果如表3所示. 从表3可见,各监测点的拟合度变化范围为:0.958~0.973,均较接近于1,说明求解过程的拟合效果较优,所得Δa参数和Δf(a)参数的可信度相对较高.

表3 Δa 参数和Δ f(a)参数的现状计算结果Tab.3 Current calculation results of Δa parameters and Δ f(a)parameters

1)在基坑变形的多重分形谱宽度分析过程中,各监测点按Δa参数大小排序如下:可以看出,不同监测点的多重分形谱宽度存在一定差异,规律性相对一般,主要以侧位移和地表沉降变形的多重分形谱宽度相对较大,而桩顶竖向变形的多重分形谱宽度相对较小.
2)类比前述,再对Δf(a)参数按照大小排序,以评价各类大小波动的所占比例,具体如下:

可以看出,各监测点变形中大小波动的所占比例也是不同的,主要以桩顶竖向变形的大波动所占比例相对更大,而侧位移和地表沉降变形的大波动所占比例相对更小.
最后,再利用Spearman秩次检验开展Δa参数和Δf(a)参数的趋势判断,以评价基坑变形在多重分形谱宽度及各类大小波动所占比例上的发展趋势,具体分析如下:
1)多重分形谱宽度的发展趋势评价. 对Δa参数的Spearman秩次检验结果如表4所示,从表4可知,6个监测点的rs值存在一定差异,其中,地表沉降变形和侧位移变形的rs值均大于0,说明两者的Δa参数仍会进一步增加;桩顶竖向变形的rs值均小于0,说明其Δa参数会进一步下降. 因此,得出地表沉降变形和侧位移变形的多重分形谱宽度后续将会进一步增加,而桩顶竖向变形的多重分形谱宽度后续将会进一步减小.同时,按照趋势等级划分,DB24 监测点和GL11 监测点的趋势等级为Ⅰ级,其余4 个监测点的趋势等级均为Ⅱ级,趋势性均相对一般.

表4 Δa 参数的趋势判断结果Tab.4 Trend judgment results of Δa parameters
2)各类大小波动所占比例的发展趋势评价. 利用Spearman 秩次检验对Δf(a)参数的趋势性进行判断,结果如表5 所示. 从表5 可知,6 个监测点的rs值均大于0,说明各监测点均具增加趋势,且在趋势等级方面,仅CX11 监测点的趋势等级为Ⅲ级,其余监测点的趋势等级均为Ⅱ级,此参数的趋势性相较Δa参数的趋势性有所增加. 因此,得出各监测点的Δf(a)参数后期会趋于增加,那么大波动的所占比例将会趋于减小,侧面说明各监测点的后期变形以小波形为主.

表5 Δ f(a)参数的趋势判断结果Tab.5 Trend judgment results of Δ f(a) parameters
总结上述,得出基坑变形具有多重分形特征,但不同监测点的分形程度存在一定差异,如多重分形谱宽度及各类大小波动的所占比例因监测点的不同而不同,其中,地表沉降变形和侧位移变形的多重分形谱宽度后续将会进一步增加,而桩顶竖向变形的多重分形谱宽度后续将会进一步减小;各监测点的大波动所占比例均趋于减小,则后期变形以小波形为主.
2.3 基坑变形的速率比趋势判断
为充分掌握基坑变形规律,在前述基坑变形的多标度特征分析基础上,再引入速率比概念,结合Spearman 秩次检验,以开展基坑变形趋势判断研究;同时,为便于后续描述,按照监测项目类型进行统计分析,具体如下.
2.3.1 地表沉降变形的速率比趋势判断
结合地表沉降监测成果,先计算其速率比,得图2. 从图2 可知,DB8 和DB24 监测点随时间持续,其速率比存在明显的波动特征,其原因应是与基坑施工流程相关,且两者对比而言,DB8监测点的波动性相对最大. 结合速率比计算成果,将两地表沉降监测(统计周期总数为34期)的速率比分布关系详述如下:
1)DB8监测点的速率比分布. ①ε<1的监测周期数为20 期,所占比例为60.61%,其中,小于0 的周期数为5 期,所占比例为15.15%,因此,总体来说DB8 监测点的变形主要以减速变形阶段为主;②1≤ε<2 的周期数为9,所占比例为27.27%,分布比例相对一般;③ε≥2 的周期数为4 期,所占比例为12.12%,分布比例相对最少.
2)DB24监测点的速率比分布. ①ε<1 的监测周期数为17 期,所占比例为51.52%,其中,小于0 的周期数为1期,所占比例为3.03%;②1≤ε<2的周期数为16,所占比例为48.48%,分布比例与速率比小于1的分布比例相当. 未见大于2的速率比分布.
在前述速率比分布规律统计基础上,再对两者的速率比进行Spearman秩次检验,以评价两者速率比的发展趋势,所得结果如表6.
从表6可知,DB8和DB24监测点的rs值均小于0,得两者的速率比均具下降趋势,且DB24监测点的rs值的绝对值相对略大,说明其趋势性相对略强;在趋势等级方面,DB8监测的趋势等级为Ⅱ级,而DB24监测的趋势等级为Ⅲ级,两者的趋势性等级属中等偏高.
结合图2和表6中的结果,两地表沉降监测点的速率比在近期虽呈上升趋势,但后期会呈下降趋势,因此,地表沉降的后期变形会进一步增加,但增加速率会趋于减小.

图2 地表沉降变形的速率比变化趋势Fig.2 Variation trends of rate ratios of surface settlement deformations
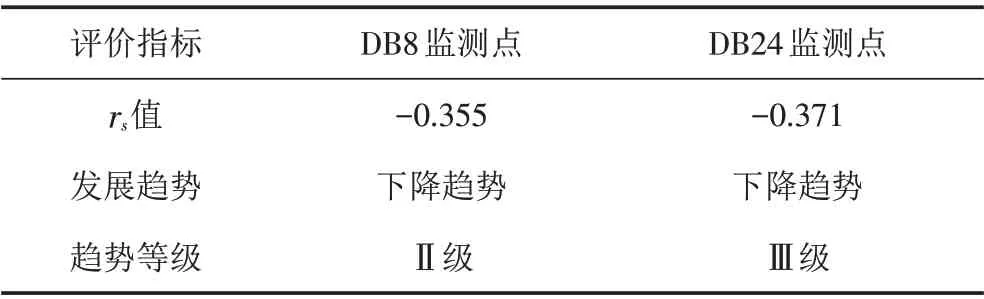
表6 地表沉降的速率比趋势判断结果Tab.6 Judgment results of rate ratio trends of surface subsidences
2.3.2 侧位移的速率比趋势判断
类比地表沉降的速率比趋势判断分析过程,对CX10 和CX11 监测点也进行速率比统计,得图3.从图3 可知,两侧位移监测点的速率比也具波动特征,并以CX11监测点的波动性相对更强.
结合速率比计算成果,将两侧位移监测点(统计周期总数为31期)的速率比分布关系详述如下:
1)CX10监测点的速率比分布. ①ε<1的监测周期数为14 期,所占比例为45.16%;②1≤ε<2 的周期数为16,所占比例为54.84%. 未见大于2的速率比分布.
2)CX11监测点的速率比分布. ①ε<1的监测周期数为12 期,所占比例为38.71%;②1≤ε<2 的周期数为18,所占比例为58.06%,分布比例相对最多;③ε≥2 的周期数为1 期,所占比例为3.23%,分布比例相对最少.
两者对比,得出CX10 监测点的速率比相对更大,且两者近期速率比均呈减小趋势. 对两侧位移监测点的速率比也进行Spearman秩次检验,所得结果如表7所示. 从表7可知,两者的rs值均小于0,说明两者的速率比后期仍会进一步减小,且两者的趋势等级相对较高,均是处于Ⅲ级.
结合图3和表7中的成果,得两侧位移监测点的速率比近期具减小趋势,且其后期发展趋势亦呈减小趋势,因此,此两监测点的后期变形具收敛特征.

表7 地表沉降的速率比趋势判断结果Tab.7 Judgment results of rate ratio trends of surface subsidences

图3 侧位移变形的速率比变化趋势Fig.3 Variation trends of rate ratios of lateral displacement deformations
2.3.3 桩顶竖向变形的速率比趋势判断
对GL10 和GL11 监测点的速率比进行计算统计,得图4. 从图4可知,桩顶竖向位移的速率比也具有较大的波动性,且两者波动性程度相当.结合速率比计算成果,将两桩顶竖向变形监测点(统计周期总数为31期)的速率比分布关系详述如下:
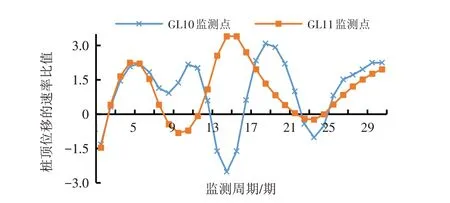
图4 桩顶竖向变形的速率比变化趋势Fig.4 Variation trends of rate ratios of pile top vertical deformations
1)GL10监测点的速率比分布. ①ε<1的监测周期数为12期,所占比例为,38.71%,其中,小于0的周期数为6期,所占比例为19.35%;②1≤ε<2的周期数为8,所占比例为25.81%;③ε≥2的周期数为11期,所占比例为35.48%.
2)GL11监测点的速率比分布. ①ε<1的监测周期数为15期,所占比例为,48.39%,其中,小于0的周期数为7期,所占比例为22.58%;②1≤ε<2的周期数为9,所占比例为29.03%;③ε≥2的周期数为7期,所占比例为22.58%.
两者对比,得出GL10 监测点的速率比相对更大,且两者近期速率比均呈增加趋势.
同理,对GL10 和GL11 监测点的速率比进行Spearman 秩次检验,结果如表8所示. 从表8可知,两桩顶竖向变形监测点的rs值亦小于0,且两者绝对值相当,说明两者速率比后续呈下降趋势,趋势性相当;在趋势等级方面,两者均处于Ⅰ级.

表8 桩顶竖向变形的速率比趋势判断结果Tab.8 Judgment results of rate ratio trends of pile top vertical deformations
总结上述,在图4结果中,两桩顶竖向变形监测点的速率比近期变化呈增加趋势,但在表8结果中,两桩顶竖向变形监测点的速率比向减小趋势方向发展,即桩顶竖向变形的后期具收敛趋势.
3 结论
通过对基坑变形的多标度特征分析及速率比趋势判断,主要得出如下结论:
1)在地表沉降变形分析方面,基坑周边的地表沉降变形具多重分形特征,且其多重分形谱宽度后续将会进一步增加,但大波动所占比例将会趋于减小. 同时,地表沉降的速率比在近期虽呈上升趋势,但后期会具下降趋势.
2)在侧位移变形分析方面,基坑侧位移变形也具多重分形特征,且其多重分形谱宽度后续将会进一步增加,但大波动所占比例将会趋于减小,这与地表变形的分形特征一致. 同时,侧位移的速率比近期具减小趋势,且其后期发展趋势亦趋于减小.
3)在桩顶竖向变形分析方面,基坑桩顶竖向变形亦具多重分形特征,且其多重分形谱宽度和大波动所占比例将会趋于减小. 同时,桩顶竖向变形的速率比近期虽呈增加趋势,但其后期发展具下降趋势.
因此,综合上述,基坑变形的多重分形特征后续会进一步加深,且变形总体趋向于收敛方向发展,本研究可为现场安全施工提供一定的理论依据.

