基于最优传质系数的槽型结构参数对液膜机械密封汽化特性影响研究

郭善友

（青岛工程职业学院，山东 青岛 266112）

两相状态下的流体膜存在较差稳定性，端面液膜完整性很容易因汽化出现破坏，进而导致密封端面磨损等问题出现。为解决相关问题，笔者采用计算流体动力学方法，分析液膜相变受到的不同传质系数影响，结合响应面法和均匀试验设计法优化分析结构参数，研究内容能够为螺旋槽机械密封在相变条件下的端面设计提供一定支持。

1 建立研究模型

为顺利开展研究，需结合图1所示的模型，该模型中的Rg、Ri、Ro分别为槽根圆半径、动环端面内半径及外半径，θ、θ1、θ2分别为螺旋角、螺旋槽槽区对应圆心角度、螺旋槽堰区对应圆心角度。

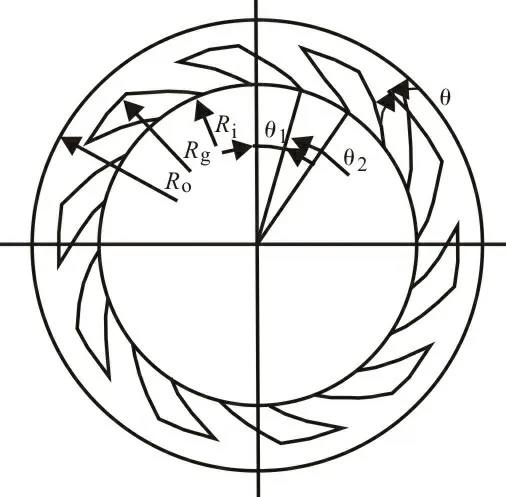
图1 动环模型示意图

为降低研究难度，设定槽堰比、槽径比分别为γ、β，具体表示为：

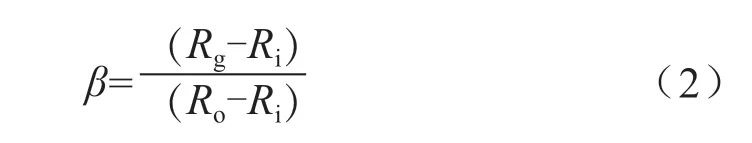
对于存在较为复杂相变机理的旋槽液膜密封来说，本研究提出以下几方面的假设：1）按照牛顿流体对流体介质进行研究；2）忽视粗糙度对流体流动造成的影响，存在光滑的密封面；3）时间不会影响流体黏度和温度，流体在密封界面间处于连续介质层流流动状态；4）时间不会影响密封环材料力学性能及温度；5）膜厚在厚度方向的密度和压力不存在变化；6）系统在工作中出现的振动及扰动影响不考虑；7）密封端面与流体介质间不存在相对滑移[1]。

2 条件设置

2.1 计算域

结合图1进行分析可以发现，动环端面上螺旋槽存在周期性分布，因此可确定各堰区和槽区存在相同的流场运动状态，为控制计算成本并提升效率，本文选择代表性槽区用于计算，同时使用Fluent软件开展研究[2]。

2.2 网格划分

对于上文确定的计算域，具体划分使用六面体结构网格，考虑到存在微米级的模型膜厚及槽深，为保证计算精度，计算域需要通过分块功能进行细分，以此得到液膜区和螺旋槽区，为同时控制整体网格质量，节点数定义需要同时围绕各区域边界开展，高精度计算可顺利实现。分析不同网格数时的平均汽相体积分数可以发现，在网格数为367 912时对应存在1.5%的相对误差，网格对平均汽相体积分数产生的影响基本可以忽略，基于控制计算成本需要，本文在网格划分中以367 912为网格数量[3]。

2.3 求解器设置

为离散控制方程，本文使用有限体积法，同时选择Mixture模型、evaporation-condensation模型作为多项流模型和相变模型，算法选择SIMPLEC，使用双精度、压力基求解器，mass transfer coefficient选择0.1、2、4、6、48，体积分数项、压力松弛因子、动量及能量项、收敛精度分别为一阶迎风格式、0.3、二阶迎风格式、10-6。

2.4 最优传质系数

结合具体计算结果进行分析可以发现，升高的传质系数对应存在变化较为明显的平均汽相体积分数，其数值提升明显，增大的传质系数对应存在急剧增大的平均汽相体积分数，但后者的增大趋势在达到一定数值后基本停止，设置传质系数为48时，对应存在较低的计算成本和较高的计算效率，因此将其作为优化传质系数开展后续研究[4]。

3 槽型结构参数影响分析

3.1 研究思路

研究需要确定固定参数，包括入口压力、出口压力、入口温度、出口温度、槽数、转速、端面内径、端面外径，分别为1 MPa、101.325 kPa、393 K、300 K、12个、3 000 r/min、26 mm、31 mm，同时槽深、槽堰比、槽径比、螺旋角参数的范围分别为3 µm～11 µm、0.1～0.9、0.1～0.9、20°～30°。

3.2 实验设计

将设计变量参数代入均匀设计表，具体使用17水平、4因素的均匀设计表U17（174）[5]，计算域几何模型需结合各组参数分别搭建，数值模拟依托CFD方法完成，其中螺旋角、槽径比、槽堰比、槽深分别记为x1、x2、x3、x4，考虑到各结构参数间存在一定程度的交互影响，因此多个二次多项式方程可基于实验结果列出，不同实验因素与响应值的关系可由此直观展示，具体的二次多项式回归方程格式为：

表1直观展示了结构参数和计算结果。

表1 结构参数和计算结果

3.3 具体分析

具体分析使用响应面法，对比槽深、槽堰比、槽径比、螺旋角两两相互作用响应面曲线及等高线图可以发现，平均汽相体积分数在给定范围内受到的最大影响源于槽径比，最小影响源于螺旋槽槽深，影响第二、第三大的分别为槽堰比、螺旋角。开展单因素分析可以发现，在螺旋角所处范围为20°～30°时，螺旋角增大对应存在随之提升的平均汽相体积分数，这是由于螺旋槽背风侧工作面面积因增大的螺旋角而减小，压力突变因此在同一时间增加，压力受此影响在槽区范围内随之减小，由此增大的低压区域对应存在同时增大的汽化相变区域，最终导致平均汽相体积分数提升；进一步分析可以发现，在增加的槽径比影响下，对应存在先提升后降低的平均汽相体积分数，最大值出现于槽径比数值为0.5时。受较小的槽径比影响，对应存在面积较小的螺旋槽背风侧工作面，在较小的压力突变区域作用下，整个液膜中低压区不够明显，无论是相变程度还是平均汽相体积分数都相对较低。但随着槽径比这一参数指标的增加，压力突变区域也会随之增大，而后续的参数数据均会受到影响出现波动。但需要注意的是，槽径比达到一定的数据后，抑制作用产生，低压区的影响链也会随之减弱，这一指标为0.5，在这一指标节点下，相变发生会受到抑制，进而影响到平均汽相体积分数。实际的数据显示，槽堰比是影响平均汽相体积分数的关键，二者之间呈现正相关。从数据的整体情况来看，槽堰比存在两个特点比较突出的数据节点，分别为0.1和0.9，在这两个数据值下，两个周期螺旋槽之间产生的堰区、槽区差异性明显，受到堰区、槽区面积大小的影响，低压区、相变区域、平均汽相体积分数都呈现出了不同的特点。当槽堰比为0.1时，槽区小、堰区大时，上述3个参数指标也相对较小；反之，当槽堰比为0.9时，槽区大、堰区小时，上述3个参数指标也相对较大[6]。

在完成单因素分析的基础上，进一步展开综合性因素分析，从而更加具体地明确不同指标之间的两两作用效果。从单因素分析视角可知，平均汽相体积分数还受到槽深这一指标参数的影响，二者之间也呈现出正相关关系，和槽堰比的影响作用相似，随着槽深的增加，低压区、相变区域、平均汽相体积分数都呈现出上涨趋势。综合考虑这些指标参数，对比分析交叉影响情况，想要得到低压区、相变区域、平均汽相体积分数的极大值，需要将槽径比控制在0.45～0.55。还要对其他参数指标数据进行控制，尤其是螺旋角这一参数指标，在螺旋角不变时，上述参数指标都会遵循相应的规律，指标参数之间的影响力不会发生改变。一旦螺旋角出现变化，那么指标参数之间的影响力会逐渐下降，即便槽径比增加，平均汽相体积分数增大趋势也会逐渐变得不明显，区别于槽径比，槽深虽然也受到了螺旋角的影响，但这一影响具体体现在螺旋角增大的基础上，槽深增大，平均汽相体积分数增大趋势更加明显，变化越发显著。由此可知，相比较槽径比，槽深和平均汽相体积分数之间的交互影响程度更为深刻。在此基础上，进一步分析平均汽相体积分数与槽径比、槽深、槽堰比三者之间的关系。当槽径比不变的情况下，槽深、槽堰比之间的关系正常、影响程度不受影响，而当槽径比出现变动的情况下，平均汽相体积分数和二者之间的关系呈现出了曲面特点，可以看出交互影响格外显著。综合各方面信息来看，随着槽深、槽堰比的增加，平均汽相体积分数整体趋势依然以向上增长为主[7]。

4 结构优化

4.1 优化模型

结合上文分析可以发现，平均汽相体积分数会直接受到端面型槽结构参数变化影响，为保证密封稳定运行，实现对汽化程度的科学控制，优化目标应设定为平均汽相体积分数，具体的优化设计需要围绕螺旋槽的槽深、螺旋角、槽堰比、槽径比共4个变量开展。回归分析均匀实验表中数据，可确定模型调整后存在接近1的拟合优度R2，同时存在0.000 1以下的显著性，因此可确定模型回归显著，能够满足研究需要[8]。进一步开展显著性检验可以发现，螺旋槽槽深与槽堰比在检验中存在非常明显的两两交互作用，同时槽深与螺旋角间存在显著的两两交互作用，显著性分别小于0.001、小于等于0.05，同时存在交互作用不显著的其余项。结合属于多元二次方程自变量系数的回归系数进行分析可以得到以下模型：

4.2 优化求解

对于上述模型，最优解在变量范围内无法直接获得，因此本文采用辅助求解方式，具体使用遗传算法工具箱Matlab，在对比多种算法后可以确定，遗传算法在本文研究中较为适用，能够较好解决组合优化的复杂问题，在遗传算法的具体应用中，具体步骤如下：第一，初始化设置。设置最大迭代数、进化迭代数计数器分别为G、t=0，初始值由随机生成个体组成。结合上文确定的变量及相关研究经验，可确定不同变量的参数范围，其中螺旋槽槽深、槽堰比、槽径比、螺旋角分别为3 µm～15 µm、0.1～0.9、0.1～0.9、10°～30°。第二，个体评价。个体适应度函数选择式（3），以此对不同个体适应度进行计算。第三，开展选择运算、变异运算、交叉运算，分别将选择算子、交叉算子、变异算子作用于群体，进而可得到下一代群体。第四，判断终止条件。对不同个体的适应度进行计算，由此得到的最优解为计算过程中的最大适应度个体，槽型结构参数优化可由此顺利实现，进而更好地满足相关研究需要[9]。

对于工作状态的汽液两相流机械密封，只有限定密封运行状态，方可保证其稳定运行，如果存在大于最大汽相体积分数的平均汽相体积分数，不稳定的液膜就会随之产生，密封失效问题也会同时产生[10]。结合相关研究可以发现，10%～25%汽相体积分数范围对应的最大膜压系数（液态水）能够有效避免密封失稳问题出现，因此本文将约束条件设定为10%汽相体积分数，因此可以得到：

基于确定的优化约束条件，确定存在满足约束条件的个体适应度后，需要对拥有最大适应度的个体进行记录。反复开展迭代计算，最终可得到优化结果，最优螺旋槽槽深、槽堰比、槽径比、螺旋角的范围分别为4.0 µm～6.0 µm、0.10～0.25、0.10～0.30、25.0°～28.0°。在本研究工况下，基于上述取值控制槽型结构参数，得到的平均汽相体积分数满足相关研究要求，可保证密封运行稳定。

5 结论

综上所述，液膜机械密封汽化特性会受到多种因素影响。在此基础上，本文开展的仿真实验研究，则确定了最优螺旋槽槽深、槽堰比、槽径比、螺旋角的范围，分别为4.0 µm～6.0 µm、0.10～0.25、0.10～0.30、25.0°～28.0°。