基于智能车快递分装装箱问题启发式混合模糊策略研究
钱 铖,王 淳,王瑞龙,陈英革
(常熟理工学院 电气与自动化工程学院,江苏 常熟 215500)
0 引言
随着国内外电商行业的蓬勃发展,对于快递运输行业的要求也越来越高.而快递装箱问题的优化求解,其基本目标是提高空间利用率(暂不考虑载重),在节约资源和提高效率方面起到重要作用.在实际应用中,快递装箱问题有不同的优化目标和装载约束,于是涌现出许多关于装箱问题的解决方法.
装箱问题属于NP-Hard问题[1],故精确求解算法对于装箱问题来说是不现实的.Lim[2]、Bortfeldt等[3]分别提出了一些启发式算法及一些三维装箱实例;Mourat等[4]提出了GRASP随机自适应启发式算法;张德富等给出了组合启发式算法[5]、砌墙式启发式算法[6]、多层启发式搜索算法[7];何大勇等[8]、张德富等[9]、李伟等[10]分别通过遗传算法来寻求装箱问题的最优解;李广强等[11]、何琨等[12]、王程等[13]还分别针对三维装箱的空间分解及布局做了相关研究.
研究上述文献后可知,这些算法更多的是强调填充率和最优装填搜索,而针对智能车快递分装的装箱问题,需求上更倾向于装填和分发的时间效率.为此,本文在前人研究的基础上,加强了装箱问题的约束,并以拟人的启发式算法为基础,将目标分解成子目标进行逐层装填,并在子目标实现中采用贪心算法,以提高目标达成的科学性和合理性.在降低数据的搜索维度方面,依据快递货物的特点,当箱体尺寸小于某一个阈值时,采用模糊策略进行改造移植,进一步满足实用性需求,最终得到适合快递车智能化改造的装箱算法HHFS(Heuristic hybrid fuzzy strategy).对于边长100~200 cm强异构的装箱问题的仿真测试结果表明:此混合算法不仅在填充率上不输以往结果数据,同时还具有提取过程中减少箱体往复搬运,适应快递多点分发的优点.
1 装箱问题模型
1.1 一般装箱问题描述和约束条件
Dyckhoff和Finke[1]概述了不同类型的装箱问题.本文所研究的三维快递分装装箱问题属于装箱问题中的一类,可以形式化定义如下:
给定一个容器(其体积为V)和一系列待装载的货物.假定容器和货物的形状都是长方体,需确定一个可行的货物放置方案,使得在满足给定装载约束的情况下,容器中包含的货物总体积S尽可能大,即填充率filling rate = (S/V* 100%) 尽可能大.其约束条件应满足以下3个条件:
(1)被装载的货物必须完全被包含在容器中;
(2)任何两个被装载的货物不能空间互相重叠;
(3)所有被装载的货物以与容器平行的方式放置,即不能斜放.
1.2 智能车快递分装问题的约束条件强化
基于智能车的快递分装还需要进一步考虑快递分发的先后关系,因此存在堆放次序的优化问题.算法应根据快递分发目标的行程先后,目的地靠后的应放置于底层,目的地靠前的应放置于上层.在实际应用中,特定的装箱问题还有其他约束,本文对以下几个约束做了强化:
(1)方向约束:货物的装载有方向约束,也就是说,每个货物只有它的1条或几条边可以竖直放置作为高度.没有此约束的问题可以被简单地视为所有货物的3条边都可以作为高度.
(2)稳定性约束:在许多应用中,特别是在交通运输业中,装载必须满足稳定性约束.这意味着每个被装载的货物必须得到容器底部或者其他货物的支撑.即稳定性约束禁止被装载的货物悬空.
(3)基于智能车快递分装的放置方案必须满足上述两个约束条件.同时,快递的包装种类繁复,所有3条边长不同且方向约束也不同即属于异构装箱问题.本文主要考虑异构装箱问题.
(4)出于快递分发的考虑,基于智能车快递分装的放置方案的优化目标,还要考虑分发时对于多目的地的提取优先的约束.
2 基于经验的启发式算法
启发式算法(Heuristic Algorithms)是基于直观或经验构造的算法,在计算时间、占用空间等方面有先天优势,能快速给出实例的一个可行解,缺点是可行解与最优解的偏离程度不可以预计.
2.1 容器及容器放置的空间分割策略
(1)当一个空的容器(设定长Xi、宽Yi、高Zi)占据一个规则物体(设边长分别为Aj、Bj、Cj),就把剩余空间分割成3个空间不相交的容器.鉴于智能车快递分装自下而上先进后出的特点,我们选取如图1所示的上下分割方式.同时出于稳定性考虑,在无方向约束条件下,优先选取规则货物最短边长min(aj、bj、cj)定为垂直高度放置,则分割出一个Xi*Yi*(Zi-min(Aj、Bj、Cj))容器.在图1中,我们假设Cj=min(Aj、Bj、Cj),若出现狭长容器等放置约束条件时,则优先选取规则货物次短边长为垂直高度放置,其他亦然.
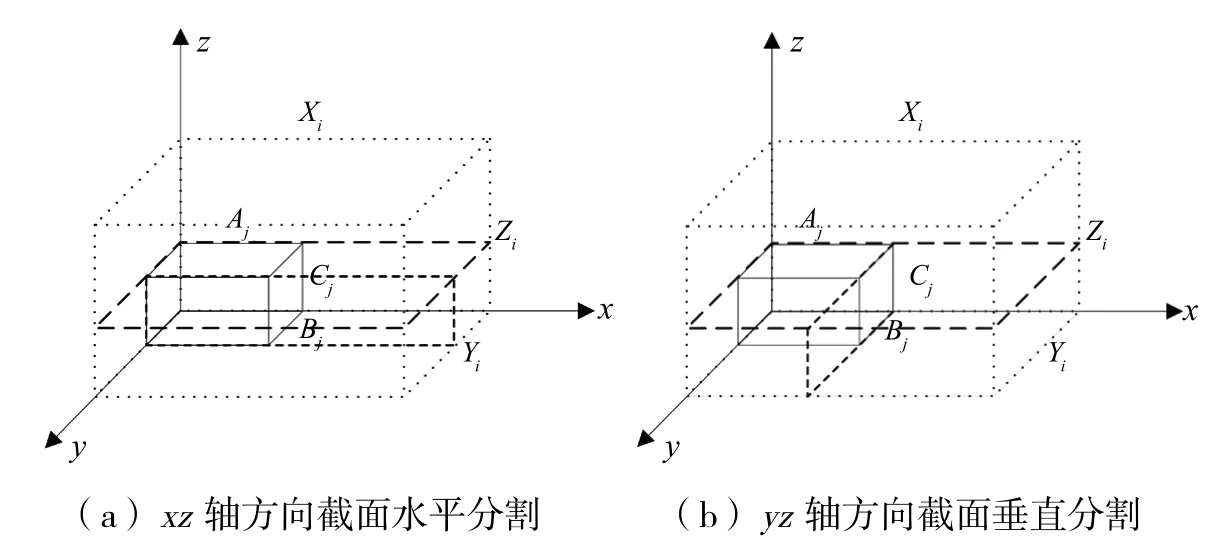
图1 快递物品在容器放置中的空间分割
(2)在z轴被确定为上下分割的前提下,x、y方向的边长又有两种分割方式,分别为xz轴方向截面分割和yz轴方向截面分割,如图 1(a)和图 1(b)所示.每种分割又有两种新容器生成的可能,如图2(a)~图2(d)所示,因此可看成是一种二维分割.
对应上述4种选项,采用贪心算法,以产生最大截面积为优选分割容器方案.

图2 快递物品在容器放置中的进一步二维分割
(3)若容器体积小于某一个阈值,则不再继续被分割,而作为小型货物填充空间碎片使用.
2.2 货物择取优先级策略及放置容器优先级策略
根据智能车快递分装稳固性及取件整体先进后出的特点,择取货物优先级和选取容器的优先级做如下设定:
(1)快递货物根据货物“体积”和货物“目的地”两个要素,采用二级优先级进行分配;
(2)“目的地”要素:对快递货物的目的地先后顺序进行编排,货物目的地次序越靠后的优先级越高;
(3)“体积”要素:对于同一目的地的货物,体积越大则优先级越高;
(4)融入模糊策略:当货物最大边长小于某一个阈值时,将其定义为容器碎片填充货物,计算中用给定的填充率经验值消耗容器碎片.如果同为容器碎片填充货物的,则依据目的地优先原则选取;
(5)在容器选取上,依次对具有最高优先级的货物分配容器,以容器体积从小到大的顺序安排容器.若货物能容纳则分配该容器,并对此容器按1.1节所述进行容器放置的空间分割.
2.3 上述算法的优点与缺陷
基于经验的启发式算法在智能车快递的分装中不仅考虑了货物填充率参数,还考虑了提取货物的优先级参数来分配容器.该算法简单、易于机器快速实现.但通过仿真结果观测发现上述算法还存在两个致命缺陷.
(1)大货物单侧堆积效应:由于同目的地大货物优先级较高,优先安排分配容器,而可分配的优选容器基本是挨着前一个更大货物,很容易形成大货物如图3所示的集中单侧堆积效应.
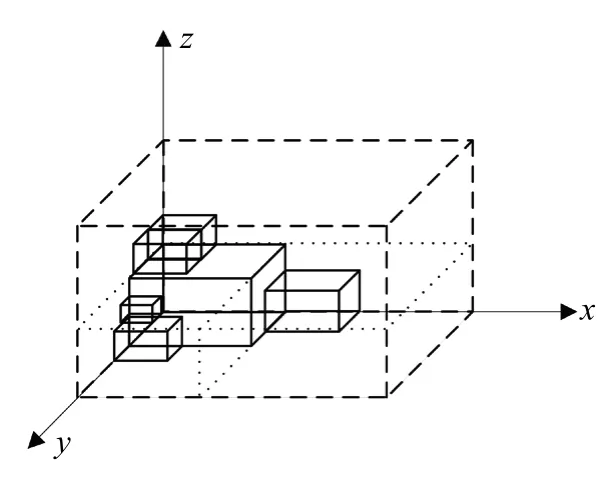
图3 快递物品的集中单侧堆积效应
(2)对于目的地优先级高的大货物,堆积到上层时,若其底面积较大,很容易出现底部支撑度不足的情况,从而会降低货物装箱的稳定性,如图4所示.
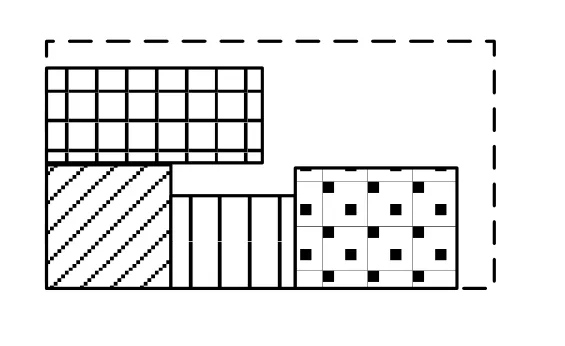
图4 快递物品堆积的底部支撑度不足现象
因此,我们修正了选取货物和放置容器优先级策略,拟人地消除每一层间的空隙.
3 快递装箱启发式混合模糊算法
在容器及容器放置的空间分割策略中实际上隐含了“层”的概念.若存在一个容器,其边长等于整个箱体对应的两个边,此容器必然在箱体顶部.若这个容器一旦被分配,则产生货物堆积的最高高度,此高度对应的面就是新的层.
依据人工平时货物装箱的经验,对于引发产生新层容器的货物选取时不再以提取同优先级中体积最大货物为选取对象,而应以最短边长为最大值(即货物隐含高度)作为选取对象,因为其决定了新的层高参照.
同时,在确定了一个新层后,应尽量填充这个层为子目标,且应不破坏此层高.在达成子目标后再生成新的层,以此类推.
在对一个层的填充过程中,我们选用贪心算法:优先选取放置后所需产生的容器新分割的容器数量最少为原则,否则选取容器总空间为最小的贪心选择条件.下面是在子层填充中引入贪心子算法的修正:
(1)当产生一个新层i时,首先确定应参与本层搜索的货物队列子集Cargo_queuei,以目的地Destination_leveli优先级最高为优先选择标准.若同一目的地的货物体积Size_leveli总和大于此新层的容器体积总和,则采纳此目的地的货物作为参与搜索的货物队列子集Cargo_queue_subj,否则搜索范围扩展到次优目的地货物,直到满足搜索范围内货物体积总和大于此新层的剩余容器空间总和.
(2)在层搜索子集货物中,依据贪心算法,遍历选取货物,并遍历容器Volumetric_queuek.贪心优选条件是:优先选取放置该货物时所产生的新分割容器数K最少的货物,否则选取体积最大的货物.选中该货物后,将其从层搜索子集链表Cargo_queue_subj中删除.
(3)依次执行(2),若在层搜索子集中选取任何货物时都将产生新层,则将此层的碎片容器用之前定义的容器碎片填充货物进行填充.结束此层子模块计算,并将层搜索子集带入下一层计算.
具体算法流程如图5所示.采用这个方法的好处是:
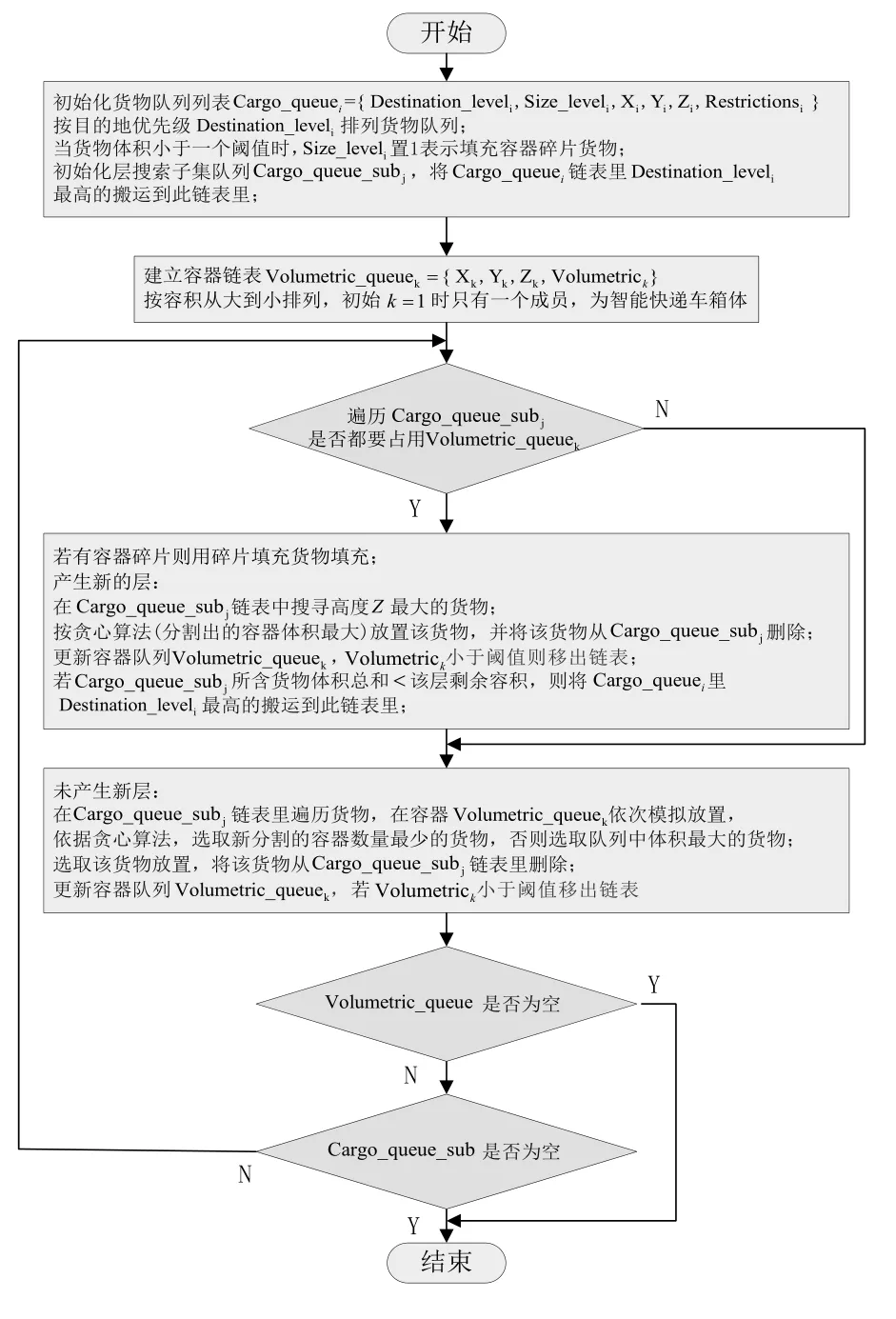
图5 快递装箱启发式混合模糊算法HHFS流程图
(1)可以优先选取与容器尺寸相符的货物,恰当地消耗容器队列;
(2)若不然,拟人地优选比较大的货物快速填充此层;
(3)算法仅做了小范围的遍历搜索,相对科学合理,算法复杂度为O(n2),满足应用的时效性需求;
(4)虽然达不到最优解,但综合填充率、先进后出命中率、时效性等整体性能满足智能车快递装载的迫切需求.
4 仿真实验与分析
本文的HHFS算法以C++在Windows 10环境下实现,处理器为Intel(R) Core(TM)i7-7700HQ CPU @ 2.80 GHz.在实验中,设置假想智能车快递分装箱体容器长X1=200 cm、宽Y1=150 cm、高X1=150 cm;货物数据集的长Xi、宽Yi、高Zi在5~50 cm范围内随机生成.为近似应用,同时做了最长边/最短边≤2的约束;朝向摆放约束随机概率5%生成;货物总体积>箱体总体积时结束数据集生成.另外,货物目的地Destination_leveli=random{3、4、5};碎片容器体积阈值设置为200 cm3;填充碎片容器货物体积阈值设置为100 cm3;碎片填充率的经验值设置为0.6.按照上述的约束设置,分别生成了20组数据,如表1所示.
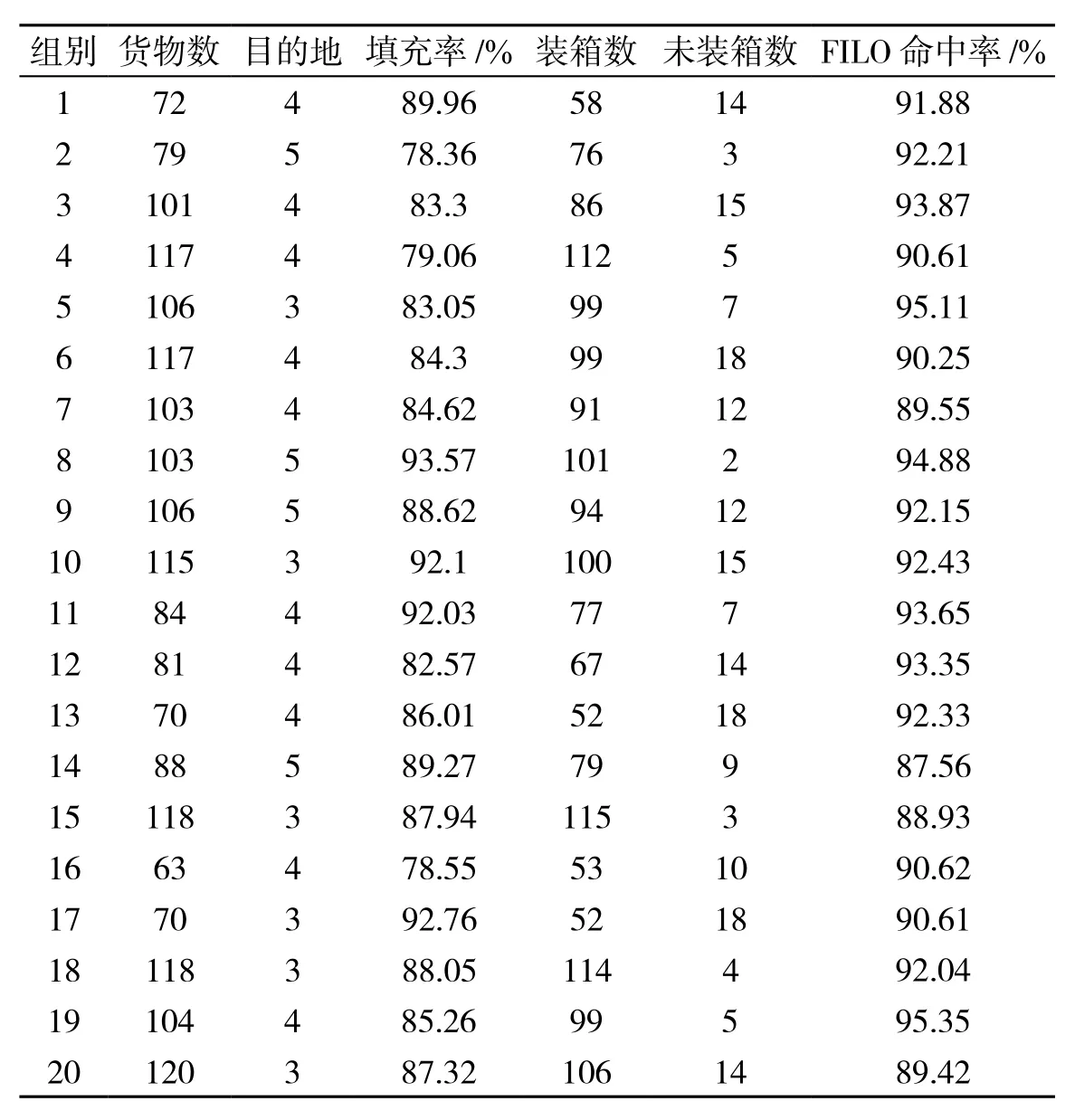
表1 20组快递货物FFHS仿真数据
为了验证本文所提算法的有效性,我们将快递装箱启发式混合模糊算法FFHS与文献[13]中的最优剩余空间算法Optimal Algorithm of Remaining Space以及文献[8]中的混合模拟退火算法Hybrid Simulated Annealing Algorithm进行了分析对比,分别考察了填充率Filling rate、先进后出命中率FILO rate以及运行时长Run time,结果分别如图6、图7、图8所示.
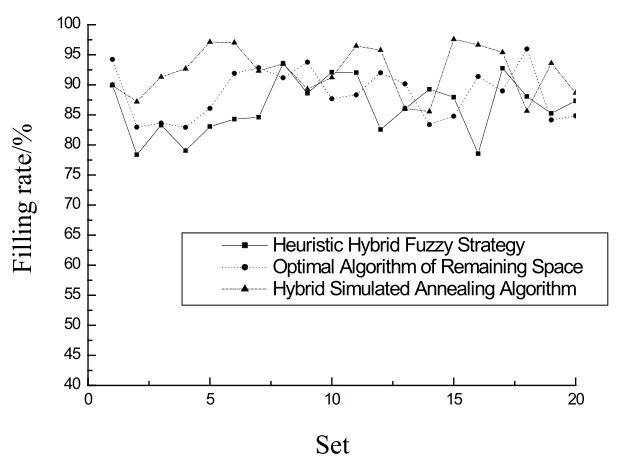
图6 货物填充率对比分析
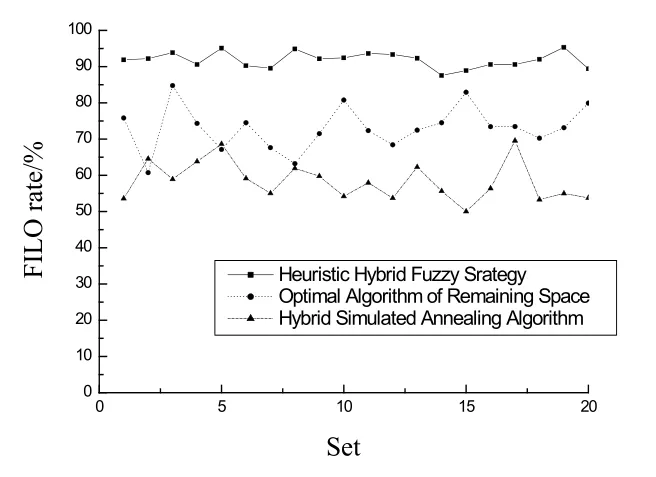
图7 货物FILO命中率对比分析
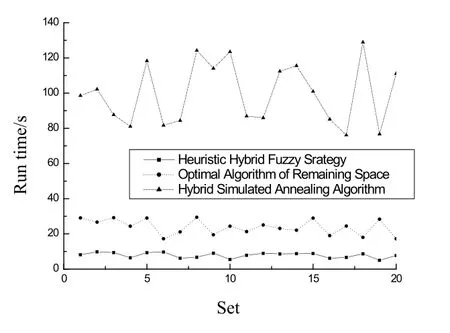
图8 算法Run time对比分析
3个算法在填充率的整体表现上都存在明显的波动,说明对于强异构性的装箱问题,其优化的策略及所采用的参数对结果都会有很大的影响.无论是策略还是参数在实际的应用中都难以得到最优的抉择.一般来说,遍历搜索越深,则填充率越高.在图6中,Hybrid Simulated Annealing Algorithm 的填充率平均为91.372%,Optimal Algorithm of Remaining Space平均为88.213%,本文的Heuristic hybrid fuzzy strategy 平均为86.335%.
在FILO先进后出的命中率方面,Optimal Algorithm of Remaining Space做了局部约束处理,Hybrid Simulated Annealing Algorithm没有做约束,而本文在寻求货物装载的稳定性目标上,对先进后出约束做了轻微弱化.从图7可以看出,仿真结果表现良好,平均达到了91.84%.Optimal Algorithm of Remaining Space平均为72.92%,Hybrid Simulated Annealing Algorithm平均为60.96%.
在程序运行时长方面,本文的Heuristic hybrid fuzzy strategy和Optimal Algorithm of Remaining Space都在减小数据搜索规模上做了工作.本文更是依据实际应用拟人地引入了模糊数学理论,在数据搜索规模上做了更进一步的缩减.图8的仿真结果表明,在运行时长方面取得了相当的优势.本文运算时间平均为7.86 s,而Hybrid Simulated Annealing Algorithm平均为100.93 s、Optimal Algorithm of Remaining Space 平均为 23.76 s.
5 结论
本文在吸收消化以往诸多装箱算法的基础上,针对快递分装更强调装填和分发时间效率的特点,提出了快递装箱启发式混合模糊算法HHFS,将启发式算法、贪心算法以及模糊算法有机结合应用于快递分装策略的计算过程中,最终形成了一套适合快递分装行业智能化控制改造方案,以贴合实际的装填操作.仿真实验结果表明这是一套值得推广的实用算法.
尽管本文针对三维装箱问题中取件的便利性、装箱的稳定性以及实施的时效性,有针对性地展开了综合性的初步探究,但算法上还有较大的提升空间.比如对于每个层的平整性问题,同样可以在数据搜索中加强优化,以进一步提高装载支撑的稳定性,这也是下一步的工作.

