G-DINA认知诊断模型族：特征、关系与新进展

杨 睿 毛秀珍 何 洁 王 霞

一、引言

认知诊断理论（cognitive diagnostic theory，CDT）是认知心理学与心理测量学相结合的产物。它根据作答反应与项目特征，运用认知诊断模型（cognitive diagnostic model,CDM）诊断被试的认知结构、加工技能和认知过程，反馈个体知识结构的优势与不足，进而为未来学习提供个性化指导。CDT作为现代测量理论，引领着国际教育与心理测量理论及实践发展，得到了广泛关注与深入研究。

认知诊断可以分析连续潜在特质、诊断离散知识结构，还可以同时评估个体潜在特质和知识结构。潜在特质模型、潜在分类模型、非参数人工智能和证据中心设计是四类主要的认知诊断方法[1]。特别地，DiBello，Roussos和Stout从一般到特殊的视角系统介绍了潜在特质和潜在分类模型[2]；Fu和Li介绍了60多种潜在分类模型[3]。

模型研究是认知诊断理论的核心，近二十年来得到了极大的丰富和发展。CDM经历了从单一测验条件到复杂测验条件模型、从低阶到高阶模型、从特殊到一般模型的发展特点。首先，项目计分方式是最基础的测验条件，通过考查属性多级计分、多解题策略推动了复杂测验条件下CDM的研究。其次，借鉴结构方程模型思想，CDM从低阶潜类别模型发展到结合潜在特质与离散知识结构的高阶CDM。最后，CDM从常用的决定型输入、噪音“与”门模型（deterministic inputs,noisy“and”gate model,DINA），决定型输入、噪音“或”门模型（deterministic input,noisy“or”gate,DINO），加性认知诊断模型（the additive CDM,A-CDM）和缩减的重参数化统一模型（reduced reparameterized unified model,RRUM）等发展到一般化认知诊断模型。Ma和de la Tore[4]总结了三类一般化诊断模型：一般化DINA模型（the generalized DINA model,G-DINA）[5]、一般诊断模型（a general diagnostic model,GDM）[6]和对数线性认知诊断模型（the log-linear cognitive model,LCDM）[7]。

一般化CDM具有一般化饱和结构，约束条件少、参数多、表达式复杂，适用范围广。de la Torre通过不同链接函数证明了DINA、DINO、A-CDM和RRUM等都是约束化G-DINA模型[5]。事实上，大部分CDM都与G-DINA模型存在直接或间接的关联，G-DINA模型及其约束化模型几乎涵盖了现有的参数化认知诊断模型。通过梳理现有CDM，可将CDM分为二级评分模型及扩展的多级评分模型、结合属性多级、多解题策略的复杂测验条件模型以及高阶认知诊断模型。以下针对不同模型的特点、关系与实践进行评析，构建了以G-DINA模型为中心的CDM树状发展图，并对认知诊断在模型发展、参数估计和实践应用等方面的研究提出思考和建议。

二、G-DINA及其约束化CDM

（一）G-DINA模型

de la Torre将作答反应的方差分解为截距效应、项目考查属性的主效应以及属性之间各阶交互效应之和建立了G-DINA模型[5]。该模型表达的正确作答概率P(ai)在一致性、logit和log三种链接函数F(·)下具有相同表达式，即：

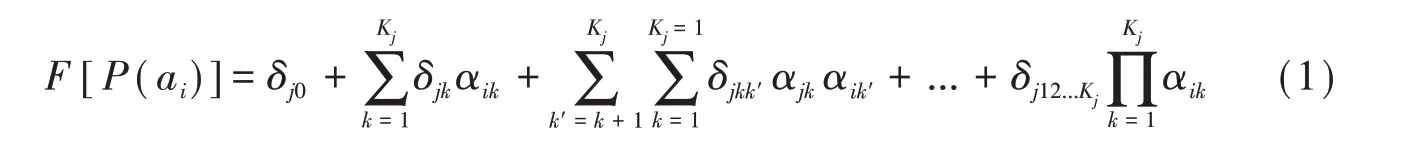
其中，δj0和δjk表示项目j的截距效应和属性k的主效应，取值非负；δjkk'，δjkk'k''，...，δj12...Kj依次代表对应属性之间的二阶、三阶到最高阶交互效应，可以取任何实数。鉴于只有项目所考查属性的子集才会影响项目作答反应，de La Torre定义了“缩减的知识状态（α*）”，以简化计算。G-DINA模型是饱和模型，参数较多，能区分所有α*的作答概率。它适用于语言诊断测试，并已广泛用于国际国内英语能力的认知诊断评估[8-10]。

（二）约束化G-DINA模型

在不同约束条件下可将G-DINA模型简化为多种常用的CDM。例如，在一致性链接下，若G-DINA的属性间不存在各阶交互效应，便得到A-CDM；若G-DINA模型的主效应δjk=0，同时除最高阶之外的各阶交互效应为0，就得到DINA模型；若G-DINA模型中属性间效应满足δjk=-δjkk'=δjkk'k''=就得到DINO模型；再如，在log链接下，若G-DINA属性间只存在主效应而不存在任何交互效应时，就是NIDA模型。G-DINA模型与常用诊断模型的关系详见de la Torre、高旭亮和涂冬波[5,11]。

目前，大部分模型都是适用于0-1计分项目的基础模型，例如G-DINA、DINA、DINO、A-CDM和RRUM模型。多级评分项目广泛存在于各类测验，在G-DINA模型基础上围绕多级评分项目迈出了扩展CDM最重要的一步。

三、多级评分CDM

等级反应模型（graded response model,GRM）、称名反应模型（nominal response model,NRM）和分部评分模型（partial credit model,PCM）是三类最常用的多级评分项目反应理论模型。CDM中，一方面借鉴GRM、PCM和NRM推广了多步骤评分项目和称名反应选择题的CDM，另一方面还发展了适用于干扰项选择题的多级评分CDM。

（一）多步骤评分CDM

1.基于GRM推广的多级评分CDM

令项目j的最高得分为mj，GRM通过相邻累积得分概率之差计算被试i在项目j上恰好得t（t∈{0 ,1,...,mj}）分的概率，即：P(xij=t|αi)=P*(xij≥t|αi)-P*(xij≥t+1|αi)。类似地，认知诊断

中令δjt=(δjt0,δjt1,...,δjt1,2,...,Kj*)表示得分大于等于t分对应于G-DINA模型的项目参数。那么链接函数F(·)下一般多级评分认知诊断模型(the general polytomous diagnosis model,GPDM)的累积概率可表示为：

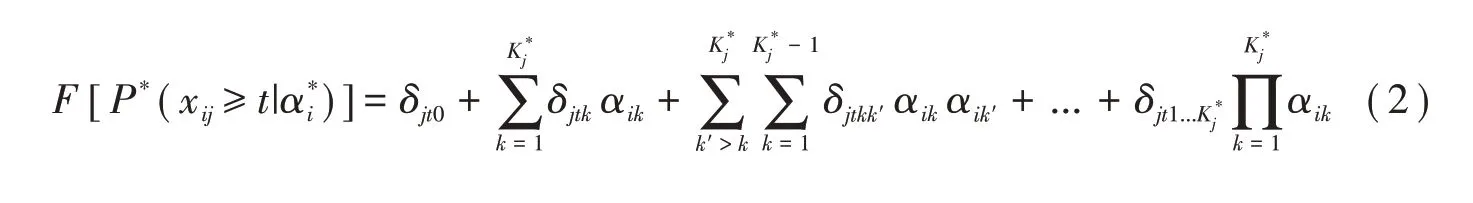
于是，GPDM的项目反应函数成为：

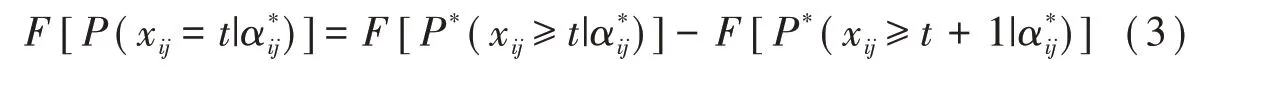
一致性链接中，累积概率模型（2）换成DINO或DINA模型，就得到多级评分DINO（polytomous-DINO,P-DINO）模型[12]和多级评分DINA（polytomous-DINA,P-DINA）模型[13]。

GPDM还可通过得分类别参数来定义，即：

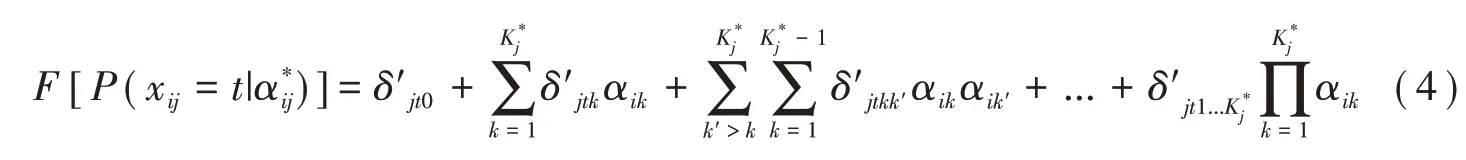
每个得分类别的项目参数是相邻累计得分类别项目参数之差，即：

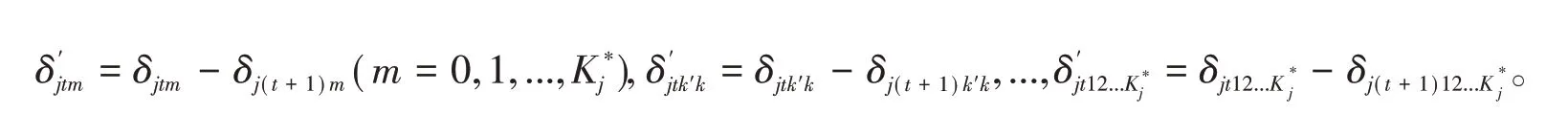
于是，多级评分项目中各个得分类别和累积得分类别q向量将变得非常重要。但GPDM、P-DINA和P-DINO均沿用传统Q矩阵的定义，没有细化不同得分类别所考查的属性。

此外，蔡艳、苗莹和涂冬波[14]指出，P-DINA和PDINO中被试往往得到极端分数，不足以反映被试间的差异。于是，他们修订了P-DINA中的理想得分指标ηij，得到GP-DINA模型。GP-DINA在参数估计、属性诊断率和实践应用方面都比P-DINA模型更具优势[15]。

2.基于PCM推广的多级评分CDM

GRM假设项目各步骤难度单调递增，PCM则强调正确作答项目需要完成若干步骤。PCM中第t步视作正确作答前t-1步条件下的0-1评分项目，仅与第t-1步相关，各步骤难度参数是独立的。基于PCM推广得到了一般化分步评分诊断模型（General Partial Credit Diagnostic Model,GPCDM）和局部或相邻类别链接函数的多级评分DINA（polytomous DINA based on local or adjacent categories link Function,LC-DINA）。

前者采用logit链接函数的定义，将G-DINA模型作为加工函数，化简得到如下表达式[16]：

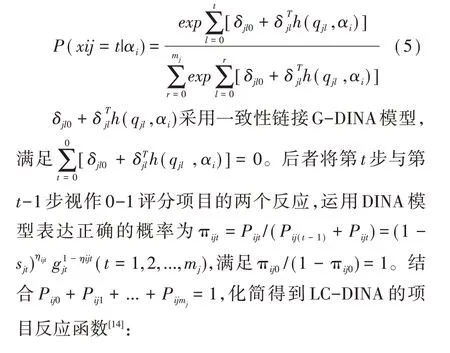
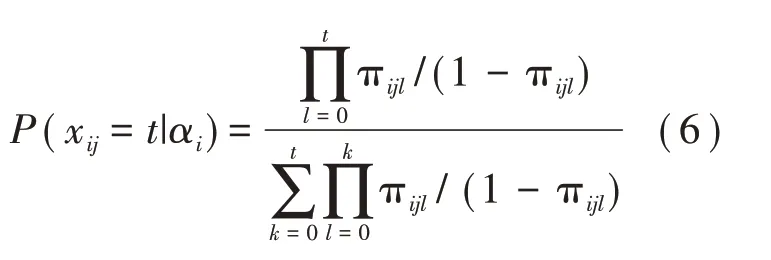
此外，与GPCDM和LC-DINA模型不同，Ma[4]和de la Torre[5]强调项目作答步骤有序，即当被试正确完成前t步，同时错误完成第t+1步时得t分。他们基于序列化思想运用加工函数建立序列过程CDM：

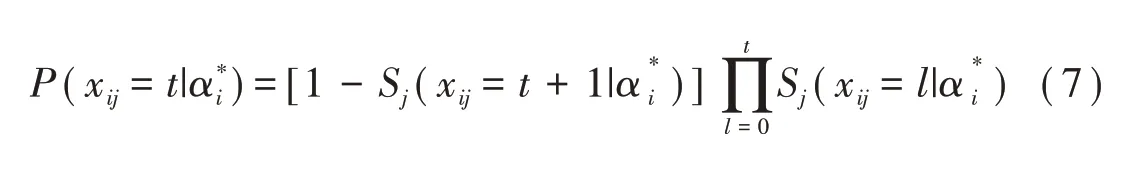
过程函数Sj(xij=t|α)表示被试正确作答第t步的概率，显然Sj(xij=0|α)=1且Sj(xij=mj+1|α)=0。当使用G-DINA模型计算过程函数S时便得到序 列G-DINA（sequential G-DINA model，Seq-GDINA）模型。

GPCDM、LC-DINA和Seq-GDINA都将项目作答视为多个步骤，基于项目作答步骤建立起项目反应模型，也都指出得分类别q向量的重要意义，并基于得分类别定义项目参数。鉴于此，Ma[17]和de la Torre[18]提出限制性和非限制性Q矩阵；苗莹[14]等和高旭亮[11]等沿用了限制性Q矩阵方法；苗莹等还建议基于GRM推广的多级评分CDM使用累加q向量[14]。此外，研究者还通过分析干扰选项的q向量提出适用于选择题的多级评分CDM。

（二）具有干扰选项的多级评分CDM

1.多选项DINA模型（multiple-choice DINA，MC-DINA）

NRM适用于称名类选择题，项目得分代表对应的选项类别。Templin,Henson,Rupp,Jang和Ahmed[19]借鉴NRM思想将LCDM模型推广到多级评分称名反应诊断模型（Nominal Response Diagnostic Model,NRDM）。

事实上，大部分选择题都设置了干扰选项。de la Torre[18]首次提出对干扰项（记其个数为）的q向量进行编码，并记非干扰选项的q向量为0，称为非编码选项。于是，选项总数记为然后依据（T表 示 转置）可将被试αi分到期望选项h'，不能被分到某个选项的被试组统一记gij=0。令第g(g∈{0,1,2,...,H*j})组被试选择每个选项的概率为P（h|g），在条件下估计参数，这就是MC-DINA模型[18]。

MC-DINA模型充分挖掘了干扰项信息，对选择题实现多级评分，具有重要意义。但其参数较多、编码选项通常不包含所有可能的属性模式，从而被试可能被分到多个干扰选项组，难以准确归类分析。鉴于此，Ozaki[20]改进MC-DINA模型提出三类结构化DINA模 型（the structured DINA models）：MC-SDINA1、MC-S-DINA2和MC-S-DINA3。

2.结构化多选项DINA模型

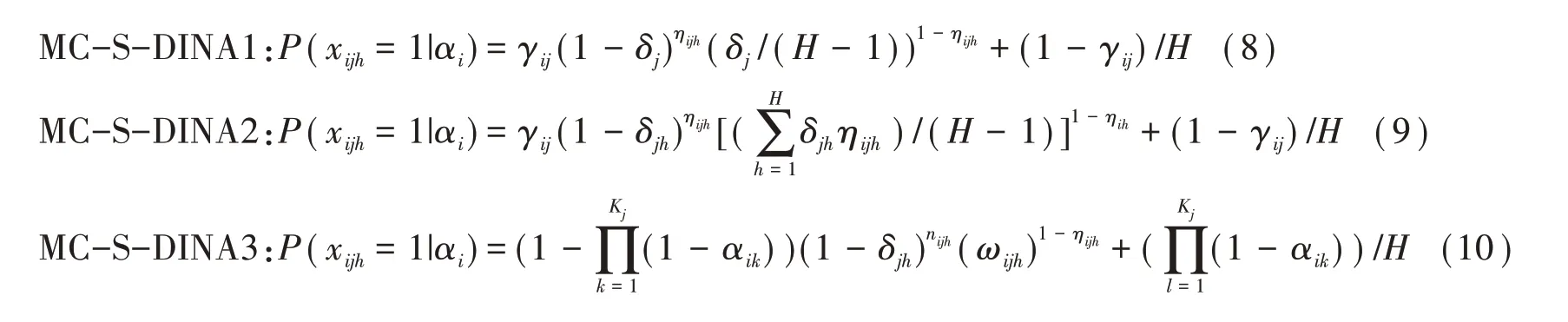
（三）多级评分CDM简评

多级评分项目CDM主要沿着两条思路展开研究。一方面借鉴GRM和PCM将常用CDM推广到多步骤计分项目，另一方面基于NRM推广了称名类项目多级评分CDM并提出具有干扰选项的多级评分选择题模型。首先，GPDM、P-DINO、P-DINA和GP-DINA都基于GRM相邻累积得分概率之差获得了得分概率模型。基于GRM推广的方法简单易行，也适用于其它约束化CDM，如A-CDM、LLM和R-RUM等。其次，GPCDM和LC-DINA是在PCM基础上推广的多级评分CDM，将第t步视为前t-1步条件下的0-1评分项目，适用于步骤间具有依赖关系的项目。而序列G-DINA则将项目作答步骤视为独立且有序的事件，适用于具有严格解题步骤的项目。再次，NRDM是基于NRM模型推广的适用于称名反应选项的一般化多级评分CDM。对NRDM取logit链接就成为参数定义在得分类别上的GPDM。最后，MC-DINA和三类MC-S-DINA模型通过分析干扰选项的特点建立了选择题的多级评分项目，开创性地挖掘了选择题中隐藏的被试内在反应过程，打破了“选择题不能提供详细作答信息”的传统观念。

项目计分方式是最基础的测验条件，也得到较为深入的研究。教育测验、心理测量和社会调查的测验情景纷繁复杂，如多解题策略、属性多级记分等都是典型的项目特征。于是，建立处理复杂测验条件的诊断模型便具有了重要意义。目前，围绕G-DINA模型，结合多解题策略和属性多级等项目特征扩展了多类CDM。

四、复杂测验条件的CDM

（一）多策略CDM

令项目j有V种解题策略，被试i运用策略v的概率为P(νij-ν|αi),P(xij+1|νij=ν,αi)为被试αi运用策略v时正确作答项目的概率。它们是建构多策略CDM的核心。

1.二级评分项目多策略DINA和RRUM模型

被试可能尝试多种策略解题，建立如下多策略CDM的一般表达式：

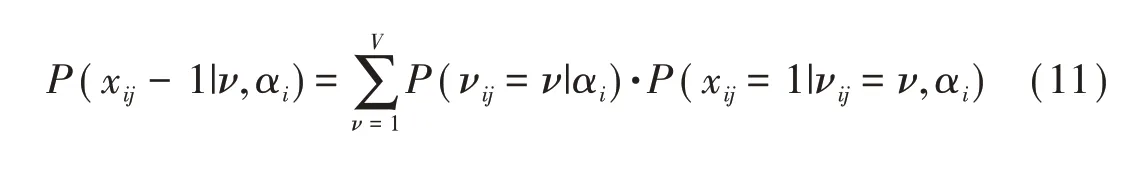
de la Torre与Douglas[21]和刘铁川，赵玉和戴海琦[22]均用DINA模型计算P(xij=1|νij=ν,αi)，分别提出了多策略DINA（multiple-strategy DINA,MS-DINA）和混合DINA模型(mixture DINA model，Mix-DINA)。不同之处在于，前者假设不同策略的失误和猜测参数相同，后者则假设它们随解题策略的不同而异。另外，P(νij=ν|αi)可以通过被试总体的表现确定解题策略的分布[22-23]，也可以结合被试掌握了哪些解题策略所运用的属性来判断被试的解题策略[21]。除DINA模型外，其它CDM也可用于计算P(xij=1|νij=ν,αi)，例如，运用R-RUM的多策略R-RUM模型[23]。

2.多级评分项目多策略诊断树模型

Ma[17]结合多策略模型和多级评分项目有序独立多步骤思想，提出两位数计分方案的诊断树模型(diagnostic tree model,DTM)。图1为两种解题策略满分为3的项目的诊断树结构示例图。

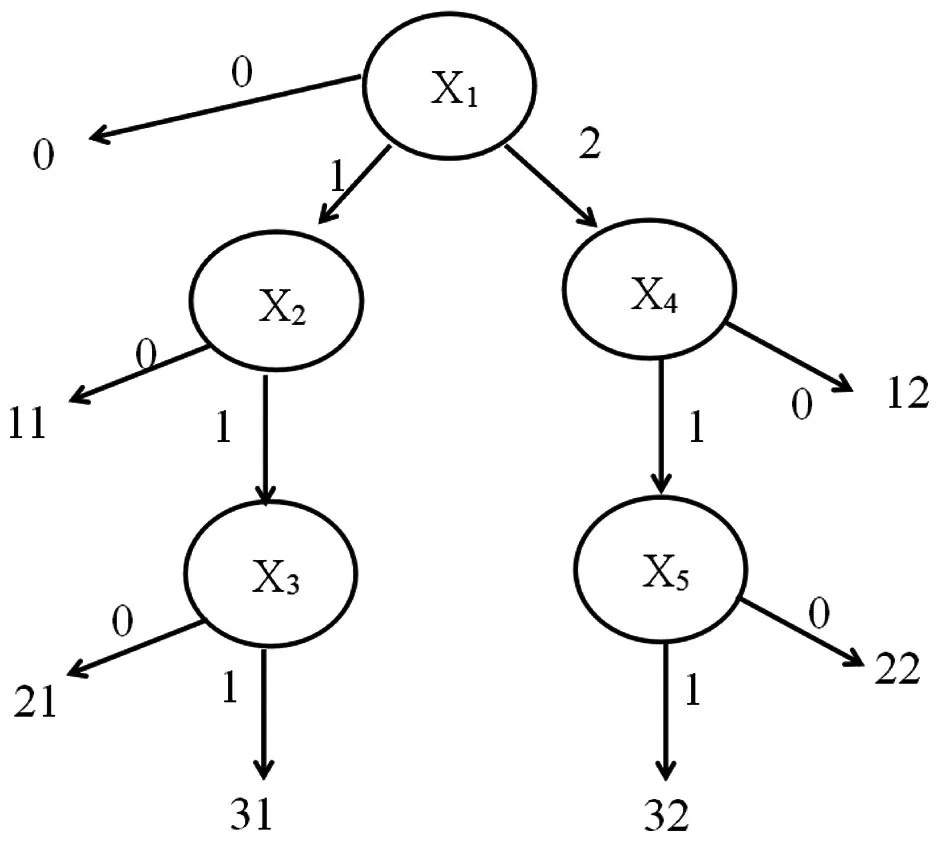
图1诊断树结构示例图

诊断树由根节点、中间节点、叶节点和路径分支组成。其中，x1为根节点，代表作答起点，包含所有作答策略分支。每一策略可形成多条路径。每条路径包含中间节点（如x2,x3;x4,x5）和由两位数构成的叶节点。其中，叶节点的个位是解题策略码，十位是观察得分码。

于是，项目j得t分可能用了不同策略，同时又需要依次完成对应路径上的所有解题步骤。令Iνjnl表示项目j在分支v的节点n上得l分的指示函数，于是DTM表示为：

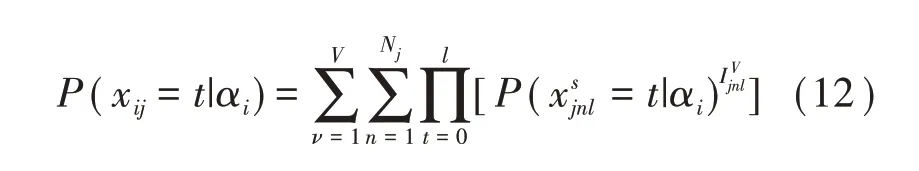
总体上讲，DTM是更一般的CDM，单策略二级和多级评分模型都是其特殊形式。由于Ma（2018）应用NRDM计算故单策略多级评分项目DTM等价于NRDM。显然，DTM中可应用其它CDM进行计算。除多解题策略外，认知诊断分析还常将属性分为多级掌握水平。特别是当认知属性粒度较大、包含内容较多时，二级掌握水平过于粗糙。因此，探索属性多级CDM也具有重要意义。

（二）属性多级CDM

属性多级情况下，q向量和α的元素都取值为多个水平。于是，最直接的方法是首先将多级向量q和α合理转化为二级向量q'和α'。事实上，只要qjk≥1就 有q'

jk=1。同时，只有当αik≥qjk时，才有代入G-DINA、DINA和RRUM模型就能得到属性多级CDM，分别记为PG-DINA、PA-DINA和PA-RRUM模型[24-25]。詹沛达，边玉芳和王立君还对PG-DINA、PA-DINA和PA-RRUM进行重参化改写，得到更简单更易于理解的等价模型[26]。CDM不仅从单测验情境向复杂测验条件发展，还结合IRT与结构方程模型思想，从低阶离散知识状态模型发展到连续潜特质与离散知识结构结合的高阶模型。

五、高阶认知诊断模型

de la Torre和Douglas[27]首次根据两参数logistic模型建构了高阶潜在特质与知识状态的关系，即：

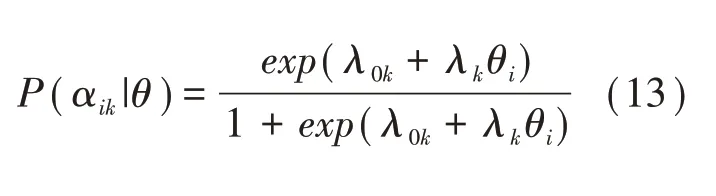
高阶DINA（high order-DINA,HO-DINA）模型通过路径难度λ0k和区分度λk建立了高阶潜在特质θ与属性αik的关系，可用于模拟研究和实证数据分析。特别地，HO-DINA中θ指各个属性共同相关的那部分潜在特质，与IRT中的θ意义不同，但二者通常存在中高等相关。HO-DINA模型对于推测被试离散的α和θ开拓了新的视角和方法，具有重要应用价值。例如，赵顶位和戴海琦运用HO-DINA模型对4～8年级学生几何类比推理中所涉及的七个认知属性进行诊断评估[28]；涂冬波，蔡艳和戴海琦研究了HO-DINA模型下计算机化自适应测验的选题策略[29]。

HO-DINA模型可以从高阶和低阶模型两个方面进行扩展。例如，涂冬波等，易芹，田伟，杨涛，辛涛和刘彦楼分别用P-DINA和G-DINA计算HO-DINA中低阶的DINA模型得到了多级评分HO-DINA模型和高阶G-DINA模型[29-30]。又如，王丹[31]将HO-DINA中高阶的单维IRT模型推广到多维IRT模型，提出了多维HO-DINA模型，并将其应用于分析几何类比推理测验。结果发现，多维HO-DINA与HO-DINA的结果一致，且多维HO-DINA的应用范围更广。特别地，HO-DINA是HO-GDINA、HO-PDINA和MHO-DINA的特殊形式。高阶模型以CDM为低阶模型，以IRT模型为桥梁，连接了潜在特质与知识状态，符合实际情况，可视作更具一般化的CDM。

六、总结与展望

CDM是认知诊断理论研究的核心，朝着多角度向纵深方向交错发展。G-DINA模型作为二级评分项目的基础模型，是多种常用CDM的一般形式。于是，围绕G-DINA模型容易建构以多级评分、复杂测验条件和高阶三条主要发展分支的诊断模型树状图（图2）。从图2可知，在各个分支上几乎都有常用CDM的扩展模型。其中，DINA模型作为最简单的约束化G-DINA模型，是扩展得最全面的基础模型之一。以G-DINA模型为核心的树状脉络图涵盖了多类重要的参数化认知诊断模型，对于厘清模型发展方向具有重要意义。总结CDM的发展不难发现以下问题还值得关注和深入研究。

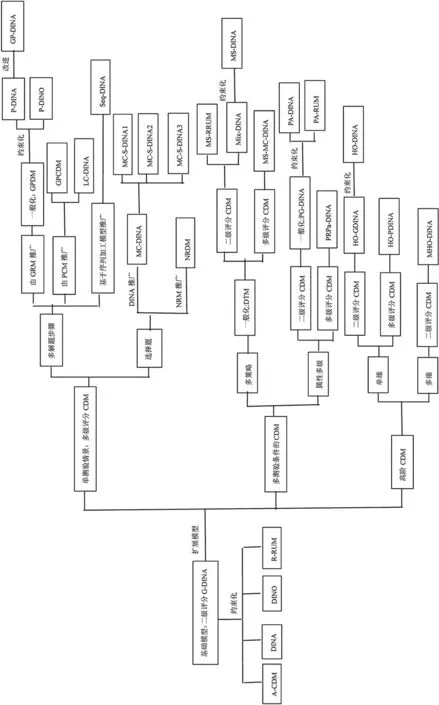
图2

首先，模型发展不均衡。限于篇幅，本文仅概述了几类依据项目特征发展的模型。不难发现，多级评分项目CDM是主体，多策略、属性多级和高阶模型的研究有待完善并进行比较。虽然CDM还朝着复杂测验条件发展，例如多级评分多策略模型、多级评分高阶模型、多级评分属性多级模型[32]、多策略多选题模型（MS-MC-DINA）[33]、多阶认知诊断模型[34]，但是相关研究显然不够。此外，除项目特征外，研究者还将某些被试变量，如反应时间、判定正确答案为正确的程度或者认可某一说法的程度等，视为因变量，建立了连续DINA模型和连续G-DINA模型[35]。因此，基于被试特征的诊断模型也具有重要研究意义。

其次，CDM的一般化发展趋势明显。G-DINA、GPDM、Seq-GDINA、DTM和HO-DINA都可视作特定测验条件下的一般化CDM。例如，过程函数是Seq-GDINA的核心，除G-DINA外，可用任何CDM来计算过程函数，甚至每个得分类别都可运用不同的CDM，从而Seq-GDINA具有一般模型框架。于是，未来研究既可以比较特定条件下约束化CDM的表现，还可以探索一般化模型之间的关系、结合多测验条件发展一般化综合模型。

再次，一般化CDM的参数估计、模型拟合方法可以在一定程度上统一CDM的参数估计与模型拟合算法。目前，无论是相同模型不同估计方法间的比较，还是相同方法不同模型的对比研究都甚少。于是，研究和比较一般模型的参数估计和模型拟合方法具有重要意义。

最后，当前研究集中于CDM的理论开发与模拟，实证研究以语言测试、数学测试、学科素养测试居多。未来研究还应加强CDM在心理、教育甚至社会测量和计算机自适应测验等领域的实践应用。