基于两阶段迁移学习的电力系统暂态稳定评估框架

李保罗，孙华东，张恒旭，高 磊，徐式蕴，黄彦浩

（1. 电网智能化调度与控制教育部重点实验室（山东大学）,山东省济南市 250061；2. 中国电力科学研究院有限公司,北京市 100192）

0 引言

随着新能源渗透率不断升高,电力系统的运行面临更复杂的动态现象,暂态扰动传播速度快、范围广,一旦发生失稳,系统会遭受严重影响［1］。因此,针对新型电力系统时变性强、复杂度高等难题,提高暂态稳定评估（transient stability assessment,TSA）方法的可靠性具有重要意义［2］。

数据驱动法被广泛应用于TSA 的研究,并取得了良好的评估性能［3-5］。但这类研究假设训练数据和测试数据服从独立同分布,一旦电网的运行方式或拓扑结构发生较大变化,该假设难以成立,导致模型的评估性能受到极大影响。针对此问题,部分研究通过增强训练数据库或采用先进的建模技术来构建通用的TSA 模型。文献［6］定义重要线路集,将集合中线路停运的拓扑结构数据加入训练数据库,增强模型对拓扑变化的学习。文献［7］针对不同拓扑结构训练不同的子模型,利用马氏距离和集成学习进行综合判稳。文献［8-9］将电力系统的拓扑结构集成到图神经网络,增强模型对拓扑结构变化的鲁棒性。上述研究为通用模型的构建提供了新思路,但相似的拓扑结构会增加数据库的冗余,导致通用模型的训练难度增加。当面对未知拓扑结构时,图神经网络的评估性能会下降,需要及时更新。因此,制定更新框架是必要的。为表述方便,将模型调整期称为过渡期；将变化前和变化后的电力系统称为源域和目标域。

更新框架的研究可分为2 类:1）提高过渡期内模型的可用性；2）缩短过渡期。第1 类研究采用短时间尺度仿真的无标注样本进行更新,如文献［10］利用迁移成分分析（transfer component analysis,TCA）法对源域样本进行迁移,得到大量可用数据；文献［11］采用样本迁移和特征迁移实现了小样本条件下的快速更新。该类研究旨在短时间内将模型的性能提升至可用水平,但已有研究采用的传统迁移学习技术难以满足更新过程中端到端（end-to-end,E2E）的需求。第2 类研究采用长时间尺度仿真的标注样本进行更新,如文献［12］采用增量学习降低标注样本的需求量；文献［13］采用持续学习使得更新后的模型保持原有知识不被遗忘；文献［14］提出将最小均衡样本集和微调技术应用于更新框架；文献［15］首先生成少量标注样本,通过改进生成对抗网络生成大量同分布样本,然后将其与源域迁移样本合并用来微调模型；文献［16］利用主动学习从无标注样本中筛选高价值样本进行仿真得到其标注,并用于后续的更新过程。该类研究通过引入更多可用样本或采用样本需求量更小的算法来缩短过渡期。事实上,2 类研究具有互补性,完整的更新框架应同时涵盖2 类研究,分别实现模型可用性增强和过渡期优化,综合提高模型对电力系统的自适应性。

基于此,本文将2 类研究融合,提出一种基于两阶段迁移学习的TSA 框架。在第1 阶段,利用深度子领域自适应网络（deep subdomain adaptation network,DSAN）和少量无标注样本以E2E 的方式完成过渡期内模型的初步更新；在第2 阶段,通过样本迁移和模型迁移将评估性能提升至较高水平,缩短过渡期。算例结果表明所提框架具有完备性,2 个阶段具有良好的衔接性,能有效应对电网的突发变化。

1 数据驱动型TSA 流程

评估模型的构建分为数据库的建立、评估模型的设计和更新。数据库的建立包括数据的生成和输入特征的构建。特征构建可以从两方面考虑:1）在表征能力方面,特征应与暂态稳定性强相关；2）在鲁棒性方面,若直接采用电气量,一旦数据延时或拓扑变化,部分电气量可能缺失,而残缺的特征矩阵无法输入模型获取系统的稳定状态。因此,将故障后的母线电压视为轨迹簇,根据几何属性定义29 个输入特征［17-18］,其构建方法见附录A 表A1。稳定的判据参考暂态稳定指数MTSI:

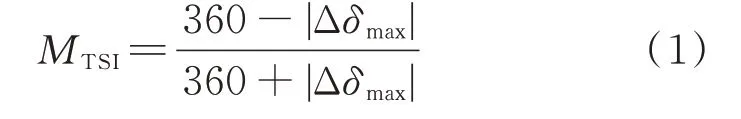
式中:Δδmax为仿真时长内任意2 台发电机转子的最大相对角度。当MTSI>0 时,系统稳定,样本标注为1；反之,样本标注为0。

评估模型的设计主要是根据任务的需求选择算法的类型和超参数,考虑到后续迁移学习的应用,选择具有灵活结构的卷积神经网络（convolutional neural network,CNN）作为TSA 模型,其结构见附录A 图A1。由于电力系统存在严重的类别不平衡现象,CNN 采用焦点损失函数,其详情见文献［19］。

评估模型的更新先根据系统的变化生成新数据,再对模型进行维护。基于深度神经网络（deep neural network,DNN）的TSA 模型,其浅层网络学习暂态特性的通用特征,而深层网络学习与具体系统强相关的专用特征,属于高阶特征层。因此,固定浅层网络,仅调整深层网络的参数即可完成更新。微调正是基于此对源域模型进行迁移,既降低了训练时间,又无形中扩充了训练数据。本文将DSAN和微调用于不同阶段以提高更新框架的完备性。

2 基于DSAN 的TSA 模型初步更新

第1 阶段旨在提高过渡期内模型的可用性,此时样本匮乏且缺乏标注,需要利用网络的表征能力完成不同域的数据分布自适应,才能学习到最优的目标域模型。

2.1 子领域自适应原理

式中:f*为目标函数；J(∙)为损失函数；f(∙)为DNN的预测函数；d(∙)为迁移正则项,通常表示源域和目标域在网络深层的全局数据分布差异；λ为正则化参数。

由于系统变化后暂态稳定性会减弱,导致源域和目标域的类别分布出现差异性。全局领域自适应后,不同类别的样本处于混淆状态,难以准确分类,如附录A 图A2（a）所示。考虑到同类别的子领域之间更具有相关性,应利用类别关系进行相关子领域对齐,使不同域的全局分布和局部分布同时被拉近,降低分类难度,如图A2（b）所示。

式中:Ec(∙)为类别c的数学期望函数。

2.2 基于局部最大均值差异的DSAN

领域自适应的核心是选择合适的迁移正则项来度量不同域的数据分布差异。最大均值差异（maximum mean discrepancy,MMD）是使用最广泛的度量之一。定义H为由显著核k定义的再生核希尔伯特空间（reproducing kernel Hillbert space,RKHS）,dH(p,q)为数据分布p和q间的MMD,即

式中:L为网络层的集合。

2.3 DSAN 的结构设计

不同运行方式或拓扑结构之间的暂态特性变化不清晰,导致不同域之间的差异性可能较大。因此,DSAN 结构的设计思路如下:1）多层适配,暂态数据的复杂性使高层的可迁移性较差,仅调整单层难以消除差异性,故对多个高层进行调整；2）采用多核-局部最大均值差异（multi-kernel-local maximum mean discrepancy,MK-LMMD）,即采用多个不同σ的高斯核的线性组合来综合衡量不同域之间的距离,增强高阶特征层的可迁移能力。

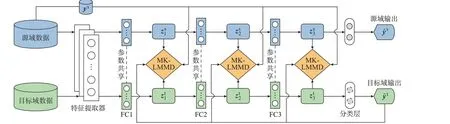
图1 DSAN 的网络结构Fig.1 Network structure of DSAN

3 基于两阶段迁移学习的TSA 框架

根据时序关系,将更新框架分为离线阶段、在线阶段、第1 阶段和第2 阶段,如图2 所示。

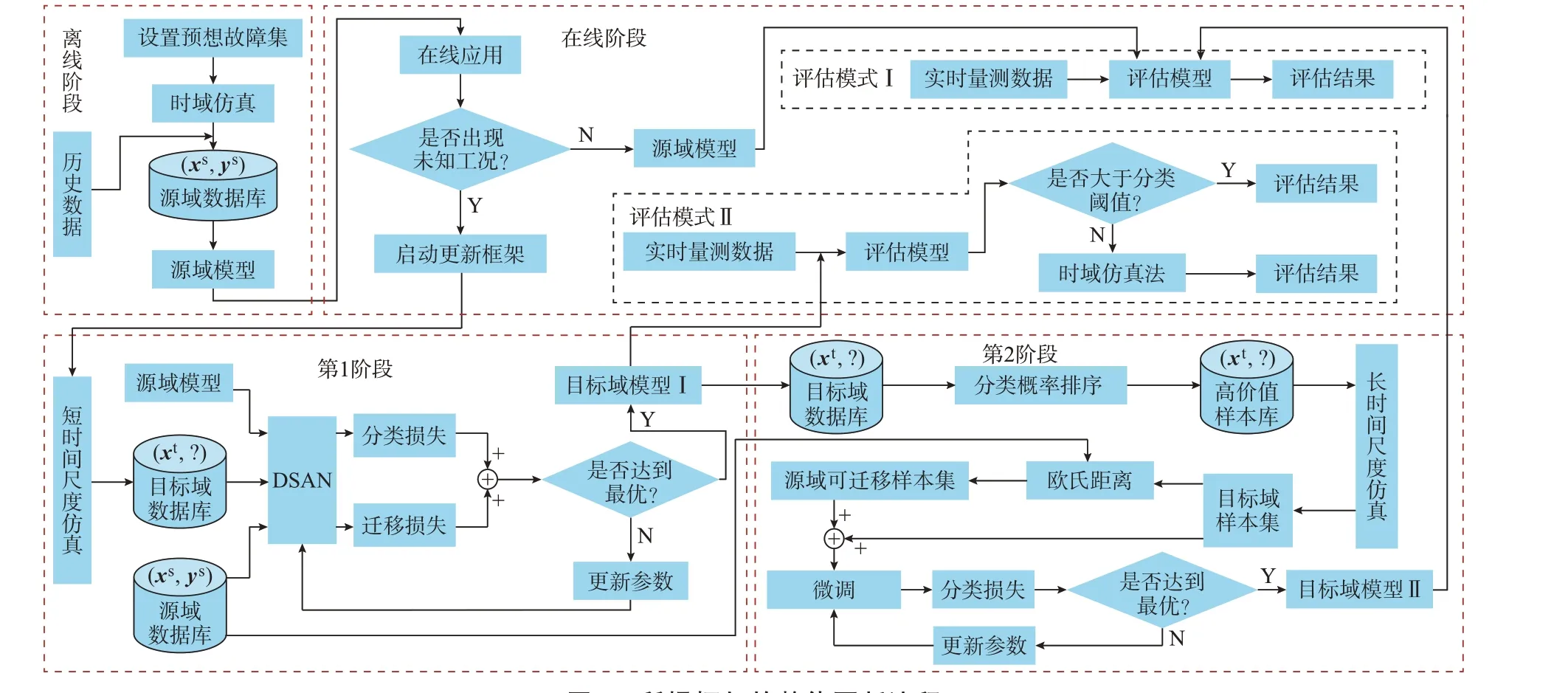
图2 所提框架的整体更新流程Fig.2 Overall updating process of proposed framework

1）离线阶段:以时域仿真为主来生成源域数据库。其中,预想故障集包括拓扑结构、发电水平、负荷水平、故障位置、故障类型和故障持续时间。

2）在线阶段:当电网处于常规运行状态时,直接利用评估模型对实时量测数据进行判稳,称为评估模式Ⅰ。当电网出现预想故障集外的运行方式或拓扑结构时,需启动第1 阶段进行初步更新,将得到的目标域模型Ⅰ用于评估模式Ⅱ。该模式先将实时测量数据输入目标域模型Ⅰ,计算分类概率。若分类概率值大于离线阶段设定的分类阈值,则直接输出评估结果；反之,利用时域仿真进行判稳。当第2阶段完成时,目标域模型Ⅱ将取代目标域模型Ⅰ,并恢复评估模式Ⅰ。

3）第1 阶段:针对未知工况进行短时间尺度仿真,生成少量无标注样本,时间尺度为故障开始后0.30 s。然后,利用源域数据库、源域模型和目标域数据库对DSAN 进行训练。当分类损失和迁移损失的加权和达到最优时,将目标域模型Ⅰ用于在线阶段的评估模式Ⅱ。

4）第2 阶段:将目标域数据库的容量扩大,利用目标域模型Ⅰ对其进行分类概率的升序排列,选取前N个样本进行长时间尺度仿真获取标注,得到目标域样本集。实际应用中根据系统需求选择N。然后,采用欧氏距离对源域中不同类别的样本进行筛选,如式（13）所示。

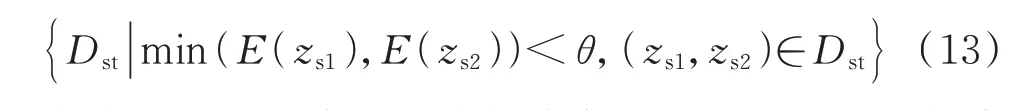
式中:Dst为源域可迁移样本集；E(∙)为欧氏距离计算函数；zs1和zs2分别为源域中稳定和失稳样本的特征；θ为距离阈值。将源域可迁移样本集与目标域样本集合并,利用微调进行训练,直到分类损失达到最优,得到目标域模型Ⅱ,结束本轮更新过程。

4 算例分析

算例采用IEEE 10 机39 节点系统验证所提框架的有效性,在中国某省级电网上验证其泛化性能和时间成本。电力系统仿真软件为PSD-BPA,深度学习框架为Pytorch。计算机配置为AMD Ryzen 7 5800 8 核3.40 GHz CPU,16 GB RAM 和NVIDIA GeForce RTX3060 显卡。

4.1 不同模型的性能对比与缺失信息测试

本实验将系统按照线路功率的传输方向划分为3 个区域,如附录A 图A3 所示。数据库的设置见附录A 表A2,其中S 表示源域数据库,A 至F 和G 至I分别表示拓扑变化和运行方式变化的目标域数据库,故障类型为三相短路,仿真时长为20 s。

为验证CNN 的评估性能,选择4 种数据驱动模型进行对比:随机森林（random forest,RF）、极限梯度提升机（extreme gradient boosting,XGB）、支持向量机（support vector machine,SVM）和DNN。RF和XGB 的基分类器个数为100；SVM 采用径向基核函数,惩罚系数为1；DNN 的结构为512-256-128-64。激活函数均为Relu,初始学习率为0.001,动量为0.95。同时,为全面评估各模型的性能,选用以下4 种评估指标:

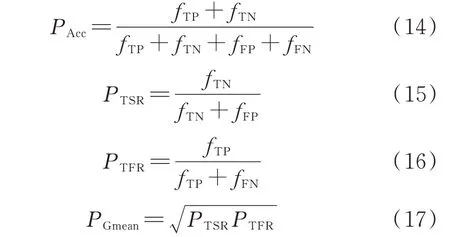
式中:fTP和fFP分别为稳定样本被正确和错误分类的数量；fTN和fFN分别为失稳样本被正确和错误分类的数量；PAcc为总体准确率；PTSR和PTFR分别为正确识别失稳样本和稳定样本的准确率；PGmean为综合性能指标。

将源域数据库S 按4∶1 划分为训练集和测试集,训练得到上述5 种模型,并在各数据库上进行测试。重复实验20 次,取均值作为最终结果,如附录A 图A4 所示。CNN 的覆盖面积最大,说明其在源域和各目标域上的评估性能均优于对比模型。由图A4（c）和（d）可知,系统的变化导致各模型的PTSR大幅度下降,而PTFR略有下降,其原因为:1）源域中稳定样本数量较多,模型充分学习了该类样本的知识；2）目标域的类别比例发生变化,原分类边界倾向将失稳样本误判为稳定。因此,后续将以PTSR和PGmean来衡量各阶段的迁移效果。

在线阶段中调度中心可能只得到部分母线的实时信息,此时基于母线电压的TSA 模型已无法应用,而轨迹簇特征仍保持维度不变,使模型可继续工作。为验证轨迹簇特征的鲁棒性,模拟母线信息缺失的情况对CNN 的性能进行测试,结果如表1 所示,其中每种测试集均由随机抽取的10 种不同母线缺失组合的数据构成。

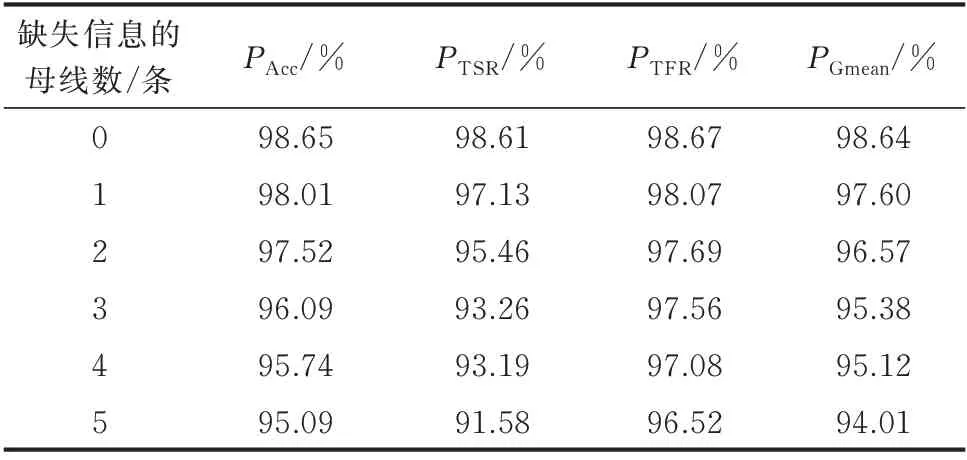
表1 缺失部分母线信息下模型的性能评估Table 1 Performance evaluation of model with missing partial bus information

由表1 可见,在缺失部分母线信息的情况下,模型仍能进行精准评估。直至缺失5 条母线信息时,PAcc仍保持在95%以上。由此可见,基于电压轨迹簇进行TSA 可有效应对信息缺失,具有独特优势。

4.2 不同目标域数据库下DSAN 的性能测试

为验证DSAN 的有效性,本实验对源域模型CNN 进行迁移,并选择4 种深度迁移学习方法作为对比:深层域混淆（deep domain confusion,DDC）、深度 适 配 网 络（deep adaptation network,DAN）、DCORAL（deep CORAL）、领 域 对 抗 神 经 网 络（domain adversarial neural network,DANN） 。DDC、DAN 和DCORAL 均 采 取DSAN 的 结 构。DDC 将MMD 嵌 入FC3；DAN 将 多 核MMD 嵌 入FC1 至FC3；DCORAL 采 用CORAL 作 为 度 量 嵌 入FC3；DANN 的结构见附录A 图A5。上述方法中迁移正则项λ为0.2,分类器和特征提取器的初始学习率分别为0.010 和0.001,每5 轮迭代学习率衰减10%。将各目标域数据库按4∶1 划分为训练集和测试集。利用上述方法将CNN 迁移到各目标域,重复实验20 次,将均值作为迁移结果,如表2 所示。其中,DSAN-1 和DSAN-3 分别表示DSAN 的单层和3 层适配。

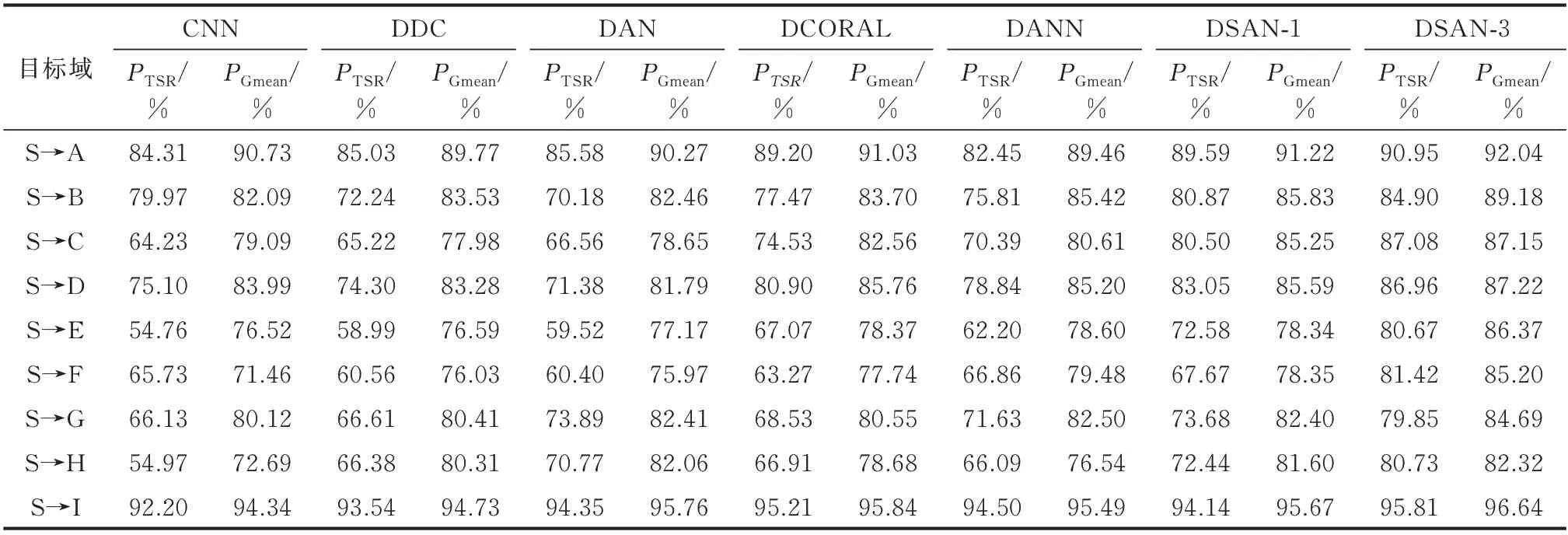
表2 不同数据库下各方法的迁移性能对比Table 2 Comparison of migration performance with each method in different databases

由表2 可知,DSAN-3 优于其他方法。DCORAL 和DANN 分别利用空间对齐法和隐式距离量度来学习领域不变特征,在多个目标域上取得了较好的迁移效果。以PTSR为准,在目标域B、D、F上,DDC 和DAN 出现负迁移现象,这证明仅拉近全局分布距离会导致不同类别的子领域过于接近,而考虑相关子领域对齐是迁移过程的关键。DSAN可捕获类别的细粒度信息,精准完成迁移过程。此外,DSAN-3 优于DSAN-1,说明增强高阶特征层的适配能力可有效提升迁移效果。

为展示各方法的随机性和差异性,将20 次迁移结果绘制成箱线图,其中,箱子的上、下边缘表示最大值和最小值,中间线表示中位数,如图3 所示。DSAN-3 的箱子整体处于最高水平。在目标域E 上对比方法的迁移效果较差,这是因为分类边界出现严重漂移,仅依靠全局域自适应难以调整,导致迁移结果的规律存在随机性。在目标域H 上对比方法迁移后CNN 对稳定样本存在过拟合,导致DSAN的箱子下边缘并未明显高于其余箱子上边缘。但DSAN 迁移后,PTSR接近PGmean,符合电力系统的误判代价不同原则,故DSAN 更适用于过渡期的迁移任务。

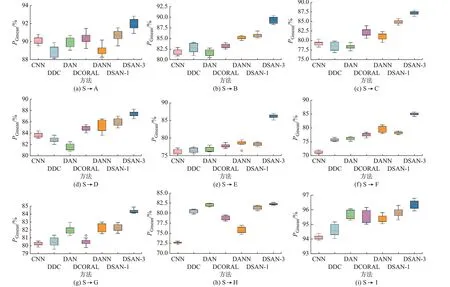
图3 重复实验下各迁移方法综合性能的箱线图Fig.3 Box plots of comprehensive performance for each transfer method in repeated tests

4.3 样本数量和分类阈值对目标域模型Ⅰ的影响

4.2 节中DSAN 利用大量样本训练取得了良好的迁移效果,但过多的样本数量会导致时间成本增加,故本节分析样本数量对迁移结果的影响。将各目标域数据库按4∶1 划分为训练集和测试集。以100 个样本为间隔,从训练集中随机抽取30 个不同规模的训练子集分别训练DSAN,利用测试集进行测试,取20 次实验结果的均值作为最终结果,如图4所示。

由图4 可知,在各目标域上,DSAN 仅需500 个样本就能大幅提升模型的性能。这是因为当少量样本能有效反映目标域的数据分布时,DSAN 就可以量度不同域的相似性,完成初步更新。当样本数量继续增加时,迁移效果不再显著提升。考虑到时间成本和评估性能之间的平衡,IEEE 10 机39 节点系统选择500 个样本进行迁移。

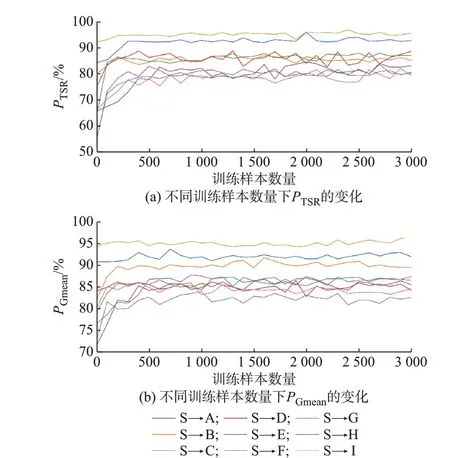
图4 样本数量对DSAN 的影响Fig.4 Impact of sample quantity on DSAN

虽然DSAN 具有时间优势,但目标域模型Ⅰ的性能难以满足TSA 的需求,须开启分类阈值筛选。在附录A 图A1 中分类层由2 个神经元组成,故输出为二维向量[ε1,ε2],其中ε1和ε2分别为样本属于稳定和失稳的概率值。将ε1和ε2中的最大值记为εmax∈[0.5,1.0]。εmax越接近1,模型将样本分类正确的概率越高；反之,分类正确的概率越低,此时属于不确定情况,须利用时域仿真法进行判稳。定义样本筛选率Pss为测试集中可由目标域模型Ⅰ直接进行判稳的样本比例,如式（18）所示。

式中:Nw为测试集中εmax大于分类阈值εt的样本数量；Nt为测试集的样本数量。为展示εt的作用,以迁移效果较差的目标域H 为例,统计不同εt下目标域模型Ⅰ的评估指标,如附录B 图B1 所示。随着εt增大,Pss逐渐下降,评估性能大幅提升。这说明将分类概率低于εt的样本视为不确定情况是合理的。考虑评估性能与Pss之间的平衡,设置最优εt为0.9。为验证最优εt的有效性,统计各目标域上目标域模型Ⅰ的性能变化,如表3 所示。

表3 中各评估指标均在95%以上,Pss均在60%以上。这证明最优εt设置为0.9 具有合理性,且与时域仿真法的结合可以增强目标域模型Ⅰ的可用性,还能减少过渡期内时域仿真的计算量。

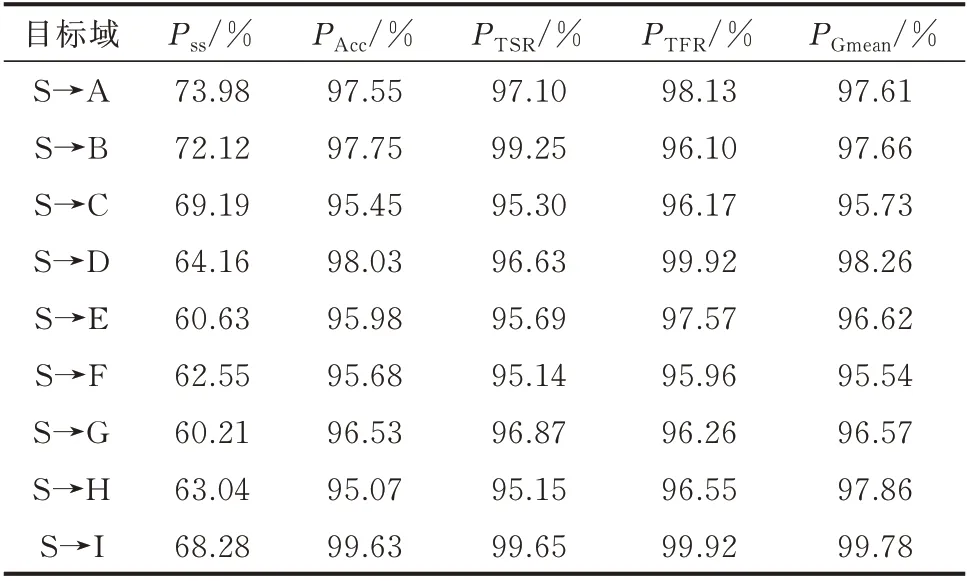
表3 最优εt下目标域模型Ⅰ的性能Table 3 Performance of target domain model Ⅰwith optimal εt

4.4 第2 阶段的迁移结果分析

为验证目标域模型Ⅱ的评估性能,本实验设置如下方案进行对比。

方案1:随机生成目标域样本集和源域可迁移样本集进行微调。

方案2:仅利用高价值目标域样本集进行微调。

方案3:利用高价值目标域样本集和源域可迁移样本进行微调。

上述方案中设置合适的距离阈值θ使得源域可迁移样本集中包含稳定和失稳样本各1 000 个,设置目标域数据库的容量为1 000,目标域样本集选取前500 个样本,取20 次实验的均值作为最终结果,如图5 所示。

由图5 可知,方案3 优于方案1,这是因为目标域模型Ⅰ已充分学习不同域之间的共性知识,利用该模型筛选的样本集能有效反映不同域之间的差异性,包含更多目标域的专有知识。同时根据欧氏距离筛选与其相似性较高的源域样本集也具有更强的可迁移性。方案3 优于方案2 也说明从源域中迁移样本能提升迁移效果。因此,方案3 充分利用目标域模型Ⅰ优化第2 阶段的评估性能和时间成本,具有较高的可行性,可作为第2 阶段的更新方案。

4.5 更新框架的综合性能对比

为验证所提框架的泛化性能和时间成本,本实验采用中国某省级电网进行测试,其500 kV 主网接线图和数据库见附录B 图B2 和附录A 表A2。其中,W 表示源域数据库；T1、T2、T3 表示目标域数据库。在第1 阶段,将目标域模型Ⅰ与TCA 对比,先确定DSAN 和TCA 所需的无标注样本数量,数据集的划分与4.3 节相同,结果分别见附录B 图B3 和图B4。在目标域T1、T2 和T3 上,DSAN 所需样本均为800,TCA 所需样本分别为1 200、1 300 和1 600,特征提取维度均为100。在第2 阶段,将目标域模型Ⅱ与主动学习对比,设置目标域数据库的容量为2 000,目标域样本集选取前800 个样本,源域迁移样本集为2 000 个样本；主动学习的查询策略为最小置信度,查询样本数量为1 100,其过程见图B5。统计各方法的评估性能和时间成本,分别如表4 和表5 所示,其中,TCA 的特征迁移时间计入训练时间。

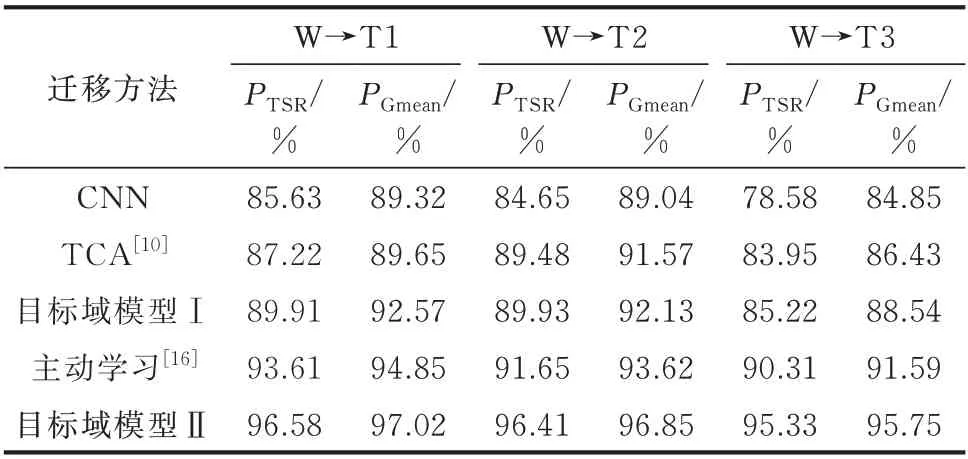
表4 中国某省级电网内不同方法的性能对比Table 4 Performance comparison of different methods in a provincial power grid of China

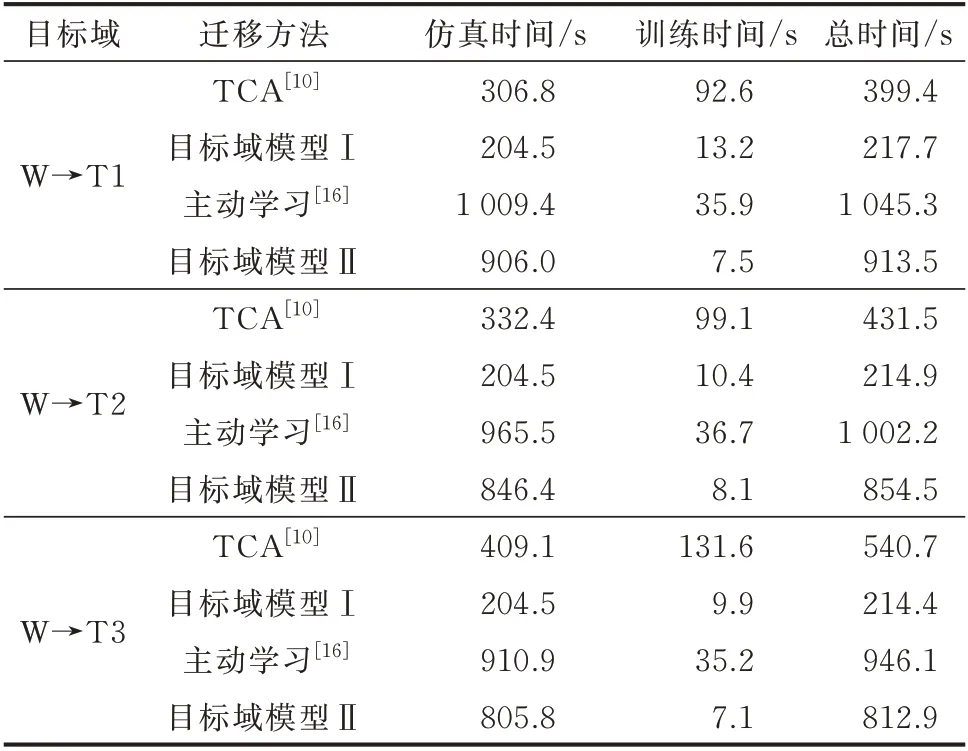
表5 中国某省级电网内不同方法的时间成本对比Table 5 Time cost comparison of different methods in a provincial power grid of China

由 表4 和 表5 可 知,与TCA 相 比,DSAN 仅需210 s 左右即可完成更新得到目标域模型Ⅰ。同时,DSAN 利用DNN 的表征能力提取更具表现力的特征,在评估性能上也取得较大优势。与主动学习相比,目标域模型Ⅱ直接学习不同域的差异性信息,无须多次迭代,且样本迁移也充分扩充了训练数据,故取得了较好的评估性能。综上,在时间上所提框架的2 个阶段具有良好的衔接性,且综合性能均优于现有框架。

5 结语

本文提出一种基于两阶段迁移学习的TSA 框架,在2 套系统上生成了多种拓扑结构和运行方式的数据库进行测试,结论如下:

1）区别于非深度迁移学习方法,第1 阶段中,DSAN 以E2E 的方式完成细粒度迁移,克服了不同域的类别分布变化,有效增强了模型的可用性；

2）第2 阶段以目标域模型Ⅰ为基础,利用高价值样本集、样本迁移和模型迁移技术有效提升模型的评估性能,降低了更新框架的时间成本；

3）相比已有研究,所提框架更具完备性。在不同的时间节点,采用无监督和有监督深度迁移学习技术更新模型,既提高了过渡期内模型的可用性,也缩短了过渡期,综合提高了数据驱动模型对电力系统的跟踪能力。

本文初步探索了将无监督和有监督深度迁移学习技术同时引入更新框架的可能性,为增强框架的完备性提供了新思路,但在更新样本生成方面仍有提升的空间和可能。后续的研究重点是开发高效样本的生成策略和增强技术,用以完善更新数据库的多样性,进一步提高更新模型的性能,并降低更新框架的时间成本。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。