基于MRMR 和双重注意力机制的城市能源多元负荷短期预测

白冰青，刘江涛，王 旭，蒋传文，江 婷，张沈习

（1. 电力传输与功率变换控制教育部重点实验室（上海交通大学）,上海市 200240；2. 南京电力设计研究院有限公司,江苏省南京市 210036）

0 引言

在“双碳”目标的背景下,城市能源系统因其能源利用效率高和可再生能源消纳比例高的优势,成为低碳化发展的重要方向［1-3］。为了保证城市能源系统的正常调度运行,需要在调度前预知系统内的负荷需求情况。但不同于传统的电力调度,城市能源系统是城市供热、供冷、供电和满足其他需求的能源系统的集合,负荷结构多样且复杂［4-5］,包含商业、办公、娱乐等多种建筑,人员分布不规律,空调等能源设备开关频繁,用户需求波动性强［6］。城市能源系统通过能源转换装置和存储装置实现能源间的联动［7-9］,能源系统在调度运行时需要考虑大量的非线性约束和离散变量,导致能源负荷彼此会受到复杂的非线性影响［10-12］。因此,城市能源系统负荷波动性强、耦合关系复杂,需要精准的多元负荷预测结果以保证能源系统的正常运行。为解决这一问题,本文提出一种基于最小冗余最大相关性（minimum redundancy maximum relevance,MRMR）方法和双重注意力（dual-attention,DA）机制的城市能源系统多元负荷短期预测方法。

现有的负荷预测方法可以分为统计方法和机器学习方法［13］。统计方法包括线性回归［14］、指数平滑［15］、自回归差分移动平均［16］等,调节参数简单且可解释性强；而机器学习方法包括支持向量机［17］、人工神经网络［18］、深度神经网络［19］、模糊逻辑［20］等,调节参数相对复杂,解释性也较弱,但预测精度高于一般统计方法［21］,是未来研究的重要方向。

在使用机器学习进行负荷预测的过程中,需要进行特征分析并建立神经网络模型。常用的特征分析方法包括协方差法、皮尔逊系数法、最大互信息系数（maximal information coefficient,MIC）法［22］和以MIC 法为基础的MRMR 方法［23］。其中,协方差法和皮尔逊系数法能够分析序列之间的线性关系,但城市能源系统中的能源耦合存在大量非线性关系,用户的用能需求也难以线性描述,更适合使用MIC法和MRMR 方法。现有研究将MIC 法应用到短期电价预测［24］,有效提高了特征序列的筛选效果,但城市能源系统中特征序列的冗余度较高,MIC 指标没有考虑这一问题,而MRMR 方法将序列中的冗余度融入筛选指标,更适用于高冗余度的城市能源系统。常用的神经网络主要有小波神经网络（wavelet neural network,WNN）［25］、卷 积 神 经 网 络（convolutional neural network,CNN）［26］、循 环 神 经网 络（recurrent neural network,RNN）［27］及 其 变种—— 长 短 期 记 忆（long short-term memory,LSTM）网络［28-29］。

CNN 和LSTM 网络已被应用于城市能源负荷预测。文献［30］使用皮尔逊系数法分析负荷与特征之间的相关性,将卷积网络和支持向量回归相结合来预测城市能源系统的负荷,但受限于分析方法,相关性分析阶段没有考虑输入信息的冗余问题。文献［31］对多能负荷进行像素重构和特征融合,在CNN-LSTM 网络的基础上结合图像识别领域的方法实现负荷预测,但特征处理工作相对复杂,且预测跨度为1 h。实际调度工作中需要更久的时间跨度,以便提前制作调度方案。在神经网络模型的基础上,可以添加注意力机制以提高网络的性能［32］。文献［33］采用灰色关联度法分析多元负荷之间的耦合性,将注意力机制应用到LSTM 网络中,验证了注意力机制的作用。文献［34］应用核主成分分析和模态分解将能源系统的负荷数据降维分解为非平稳序列和平稳序列,再分别采用深度双向LSTM 网络和多元线性回归预测最终结果,预测步长仍为1 h,仅通过降维分解对负荷特征的处理也较为有限。上述研究中建立的神经网络模型均表现为LSTM 网络或者CNN 的拼接,未将神经网络内部结构做出创新性修改以应对城市复杂能源耦合系统的预测需求。因此,可以采用LSTM 网络搭建序列到序列（sequence to sequence,Seq2Seq）结构,并辅以DA机制搭建适用于城市能源系统的神经网络模型。其中,Seq2Seq 模型在处理文本翻译、时序预测等问题时易于解释、拓展性强,具有明显优势［35］。该模型使用了2 个RNN,分别为编码器和解码器。编码器处理输入序列后生成语义向量,交由解码器生成输出序列,可以对这2 个神经网络特别设计以适用于城市能源系统。文献［36］提出了DA 机制,在解码器和编码器阶段分别加入注意力机制,以突出输入和输出环节中重要信息的作用,将其应用到城市能源系统多元负荷预测领域中,可以使Seq2Seq 模型充分学习多元能源间的耦合关系。

因此,在能源系统负荷波动性强和能源耦合关系复杂的背景下,为了提高多元负荷的预测精度,本文使用MRMR 方法筛选特征序列,在LSTM 网络的基础上,应用Seq2Seq 模型针对性地学习城市能源序列的信息,应用DA 机制加强神经网络的特征提取能力,在输出阶段考虑历史数据特征和能源系统特征以应对能源负荷的随机波动,得到间隔24 h的负荷预测结果。最后,提出一种基于MRMR 方法和DA 机制的城市能源系统多元负荷短期预测方法。主要包含以下两方面贡献:

1）针对输入数据特征处理的问题,对不同类型的数据进行无量纲化和特征序列筛选,并对比了MIC 法和MRMR 方法的原理与筛选结果,有效降低了特征序列的冗余度。实验结果表明,与MIC 法相比,采用MRMR 方法筛选的特征序列的预测精度明显提高,为城市能源系统多元负荷特征处理提供了技术基础。

2）建立基于DA 机制的Seq2Seq 神经网络,在编码器和解码器阶段都引入注意力机制,学习城市能源负荷序列的时空特征,突出其中的关键信息。实验结果表明,DA 机制提高了模型的精度和鲁棒性,可以服务于城市能源系统多元负荷预测的神经网络构建。

1 输入数据特征处理

城市能源系统的结构包括能源输入、能源转换和能源输出。电和天然气等能源进入系统后,在冷热电联供、电转气等系统内转化为电、热、冷负荷,输出给用户。这个过程中涉及的数据繁多,需要在原始数据的基础上重新调整数据格式,调整数据分布,提高数据信息密度,从而和神经网络模型匹配。因此,在进行多元负荷预测前需要进行数据预处理和特征筛选工作。

1.1 数据修正和无量纲化

城市能源系统中存储的数据存在数据缺失和数据突变的情况,本文采用插值法保证数据的平滑性。当判断原始数据为0 或突变时,使用前一时刻和后一时刻的数据平均值代替缺失数据。若出现连续数据为0 的情况,则统一使用前一时刻数据代替。

式中:dt-1为前一时刻数据；dt+1为后一时刻数据；dt和d't分别为当前时刻t修正前和修正后的数据。

城市能源系统中的数据包括能源数据和相关气象数据,都具有不同的量纲,需要进行无量纲化,使数据具有相同规格,加速神经网络的收敛。

城市能源系统中,能源负荷和气象序列的数据可以归一化到[-0.5,0.5]区间以实现无量纲化,不同于常见的[0,1]区间,神经网络偏向于以0 为中心的数据输入。因此,将归一化区间的中心设置为0有利于神经网络的收敛。数据d的表达式为:

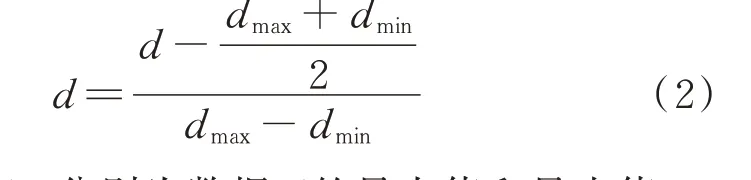
式中:dmax和dmin分别为数据d的最大值和最小值。

星期数据序列将双休日定义为0,工作日定义为1,用以分辨双休日的能源特征。时刻数据若使用[-0.5,0.5]区间,则区分度较低,所以将时刻数据[1,24]的区间映射到[0.25,6]区间上,以更大的区间范围提高对时刻信息的敏感度。

1.2 特征序列选择

城市能源系统中存在诸多类别的特征序列,包括城市能源系统内各子系统的多元负荷、新能源出力、碳排放水平、气象数据、日期数据等,需要计算这些特征序列和待预测负荷序列之间的相关性,选择合适的特征序列集合作为预测模型的输入。

为了考虑单特征变量和目标变量之间的相关性,同时考虑线性关系和非线性关系,可以选择MIC 法来判断2 个序列间的相关性。

MIC 法 由Reshef 在2011 年 提 出,可 以 有 效 检 测2 个变量之间的线性或其他函数关系［17］。MIC 法利用互信息的概念,可表示为:

式 中:dX和dY分 别 为 离 散 化 的dx和dy；a和b分 别为dX和dY方向上离散化的个数；IMIC(x,y)为序列x和y的MIC。

本文采用的数据集特征向量包含13 个负荷序列维度:电、热、冷3 种能源负荷和其他能源类型在不同时间和空间下的数据；2 个时间序列维度（时刻和星期数据）；8 个气象维度（太阳辐射、温度、湿度等）。对上述数据进行无量纲化后计算MIC,结果如图1 所示。图中,23 种特征序列每小时采集一次,共采集8 784 个点。Y1-e、Y2-h、Y3-c 分别表示待预测区域内的电、热、冷3 种负荷；e-24、h-24、c-24 分别表示输入信息中同预测时段间隔24 h 的已知电、热、冷负荷；all-e-24、all-h-24、all-c-24 分别表示城市能源系统总的电、热、冷负荷；Carbon 表示碳排放水平；Combined 表示联合机组出力；Total 表示能源负荷之和；PV 表示光伏出力；Week 表示星期数据；Time 表示时刻数据；DHI 表示太阳散射辐射；DNI表示太阳直接辐射；Humidity 表示湿度；Temperature 表示温度；Dew Point 表示露点；S Albedo 表示地表反射率；Wind Speed 表示风速；Pressure 表 示 气 压。Week 序 列 和S Albedo 序 列 与自身相关的MIC 分别为0.86 和0.89,这是因为计算MIC 时需要对给定dX、dY进行网格化,当序列为离散数据且分布非常不均匀时,同自身的MIC 很可能出现不为1 的现象,属于正常情况,不影响结论。

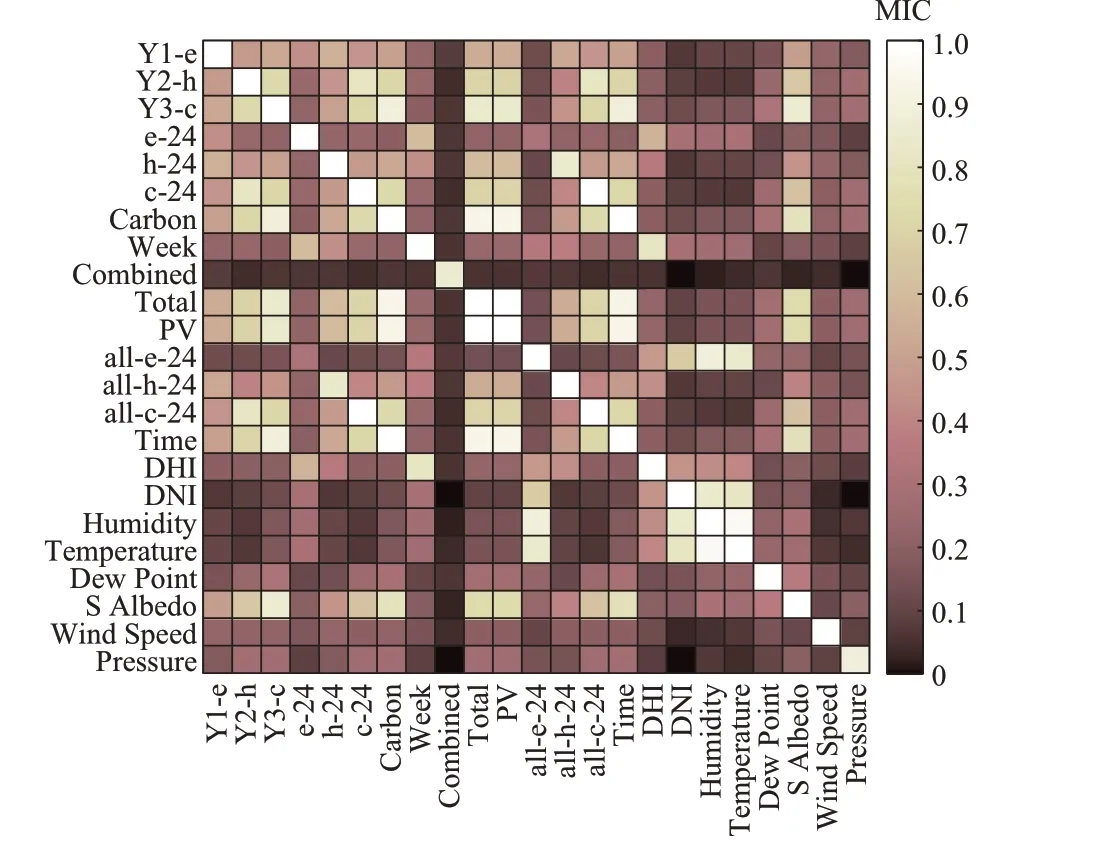
图1 各特征序列间的MICFig.1 MIC among each characteristic sequence

按照MIC 法从高到低选择的特征子集如表1 所示。可以看到,所选择的特征子集存在很多冗余信息,例如:e-24 和all-e-24 的相关性非常高（0.85）,h-24 和all-h-24 的相关性为1,信息几乎完全重复,它们不应该同时存在特征子集中；Week、Time 和Y1-e、Y1-h、Y1-c 的相关性仅为0.06、0.04 和0.06,被剔除出特征子集,但这些信息可以对时间序列进行关键判别,不应该被剔除,因此,MIC 法有待改进。

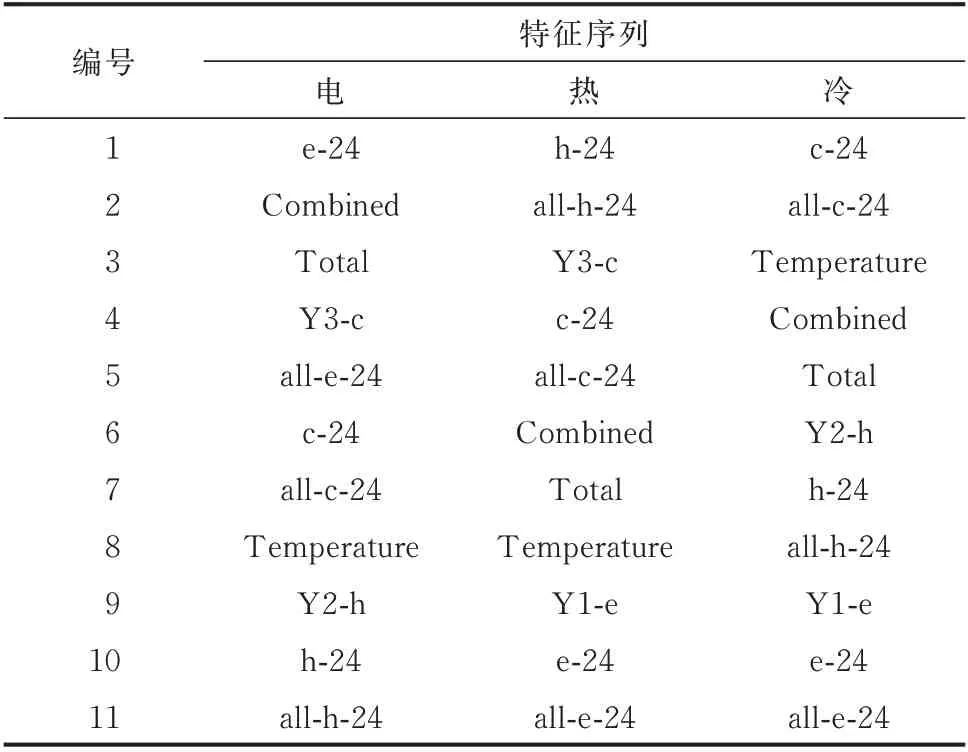
表1 采用MIC 法的特征序列选择Table 1 Selection of characteristic sequence using MIC method

为了降低特征序列的冗余性,本文在MIC 法的基础上选择MRMR 方法来实现特征选择［18］。MRMR 方法可以对已选择特征中相关性较高的冗余特征进行处罚。在所有的特征序列中,递增式地选择新的特征序列,每次都选择局部最优的特征。

定义D(S,y)为所有特征和目标变量y之间的相关度,R(S)为所有特征的冗余度,其中,S为所有特征共同构成的特征集合,即

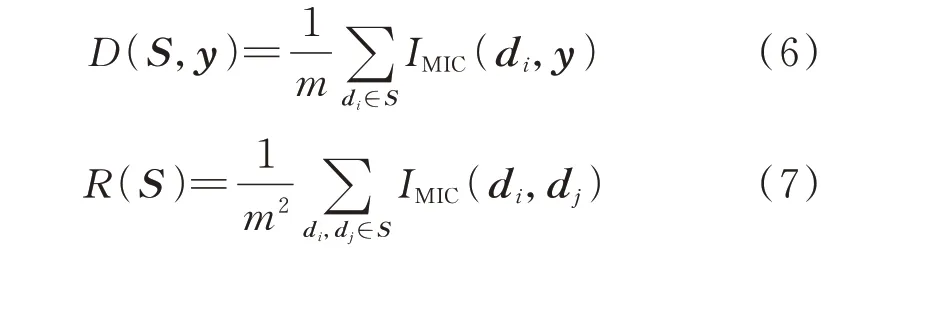
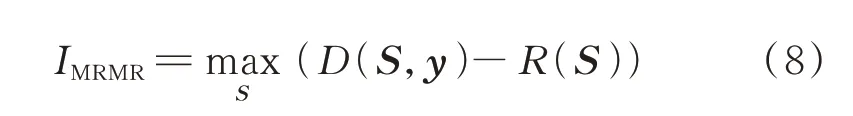
式中:di为第i个特征序列；m为最终选择的特征集合中特征序列的数量；IMRMR为特征序列的MRMR值。通过求解优化问题式（8）即可得到最终的特征子集。针对本文数据集选择的特征子集如表2所示。

表2 采用MRMR 方法的特征序列选择Table 2 Selection of characteristic sequence using MRMR method

在MRMR 方法中,重点考虑降低特征序列内部之间的冗余性,面对不同目标变量时,特征序列和目标变量之间相关性发挥的作用较小,所以3 种负荷通过MRMR 方法筛选为同一组特征序列。所选择的11 种特征序列包含常规数据中同负荷数据强相关的数据,其中湿度、太阳辐射、温度数据直接影响负荷需求,电、冷、热负荷作为直接相关的负荷数据,是负荷预测必备的输入特征,碳排放出力和光伏出力反映了综合能源系统内的能源输入和输出信息,也是关键的特征信息,同时去掉了冗余的总负荷和无关的气象信息,因此,经过MRMR 方法筛选的结果符合正常认知,是符合负荷预测需要的筛选结果。从算例结果可以看出,采用MRMR 方法的预测效果得到了提高。

2 预测模型的构建

在特征处理的基础上建立多元负荷的预测模型,考虑到城市能源系统负荷波动性强和能源耦合关系复杂,本文使用基于LSTM 网络的Seq2Seq 模型来简化预测数据输入格式的限制,引入DA 机制增强模型的特征提取能力,改善预测效果,以有效提高城市能源系统的预测精度。

2.1 Seq2Seq-LSTM 模型

Seq2Seq 模型由编码器和解码器构成。在编码器阶段将输入序列编码为指定长度的向量,在解码器阶段将编码后的向量按照神经网络训练得到的规则解码,生成输出序列。Seq2Seq 模型可以搭载多种神经网络,但一般保持编码器和解码器中的神经网络一致。本文选择LSTM 网络,这种方法适用于时间序列的处理,与注意力机制的亲和度高。LSTM 网络是一种特殊的RNN,用于解决RNN 在训练中存在的梯度爆炸或梯度消失的问题［23-24］。本文在预测模型的编码器阶段和解码器阶段分别用到了一次LSTM 网络,建立的Seq2Seq-LSTM 模型整体结构如图2 所示。

图2 Seq2Seq-LSTM 模型结构Fig.2 Structure of Seq2Seq-LSTM model

2.2 DA 机制的定义

1）注意力机制

注意力机制是神经网络中的常用模块,首先应用于机器翻译,随后在众多领域中广泛应用,因其出色的数据处理能力和良好的解释性,近年来在电力系统的负荷预测中也发挥了重要作用。

注意力机制源自对人类思维模式的模拟,人类在理解事物时会自动忽略低价值的信息,而将注意力集中到价值最高的信息上。因此,在人工神经网络中模拟这一现象,可以避免无关信息的干扰,实现信息的高效利用。在一般的神经网络中,输入资源被平均分配,而注意力机制可以根据预测对象的重要程度重新分配资源,优化资源对应的权重配比,如附录A 图A1 所示。

2）DA 机制

传统的注意力机制能够有效筛选提取模型内部信息,解决一般的RNN 中存在的输入长度、输入顺序不合理而造成收敛效率不高、信息丢失的问题,因此,在一般电力负荷的预测上具有良好的表现。但是在城市能源系统中,不同于传统电力负荷只需进行单一电力负荷预测,其同时存在冷、热、电等多种能源,不同能源之间存在复杂的耦合关系,在预测数据输入的信息中存在很多难以直观描述但关联明显的特征信息,因此需要采用DA 机制强化特征信息的提取。

DA 机制下的编码器和解码器中各包含一个注意力层,可以分别从空间和时间上寻找特征表示和目标序列之间的相关性,为不同的信息赋予不同的权重,以便更准确地预测目标序列,编码器注意力机制和解码器注意力机制的原理分别如图3和图4所示。

图3 编码器注意力机制Fig.3 Attention mechanism of encoder

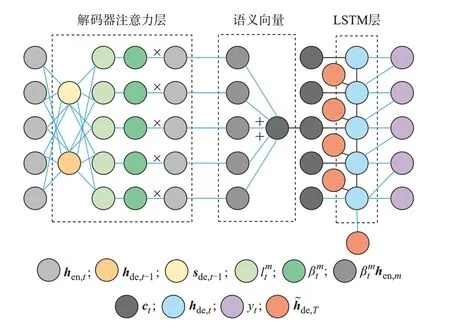
图4 解码器注意力机制Fig.4 Attention mechanism of decoder

2.3 基于DA-Seq2Seq 的城市能源系统负荷预测模型

1）编码器阶段

在编码器阶段,引入空间注意力机制在模型输入的每个时间步中进行特征提取,分析该时间步下所有特征向量序列中价值更高的一组,赋予其更高的权重,学习多元负荷同其他输入特征之间空间上的依赖关系。

2）解码器阶段

在解码器阶段,引入时间注意力机制在模型输入的多个时间步隐藏层状态中进行特征提取,分析不同时间步的隐藏层状态中价值更高的时间步,赋予其更高的权重,作为参数更新语义向量ct,并结合负荷序列的历史数据,得到最终的预测结果。

传统的Seq2Seq 模型中,对编码器输出的隐藏层状态取平均值或直接仅以T时刻编码器输出的隐藏层状态hen,T作为编码器的语义向量,但这样神经网络不能将注意力集中到关键部分。因此,可以通过解码器的注意力机制,利用解码器的隐藏层状态hde,t-1和神经元状态sde,t-1对编码器隐藏层状态hen,t进行加权平均。

首先,根据编码器隐藏层状态和解码器的神经元状态、隐藏层状态计算权重βm t:

式中:fde(⋅)为解码器阶段LSTM 函数。

3）输出阶段

在输出阶段,传统统计方法中一般会输入临近时间点的历史负荷序列和其他特征序列的集合。因此,选择hde,T代表[1,T]时段内的历史负荷特征,cT代表[1,T]时段内的能源系统特征,共同输入得到结果yT+Δt:

式中:vy、Wy、bm、b0为待学习的参数；Δt为预测负荷序列和输入的历史负荷序列的时间间隔,本文取24 h；f(y1,y2,…,yT,x1,x2,…,xT)表示最终结果由(y1,y2,…,yT)和(x1,x2,…,xT)决定。

3 预测流程

本文的预测模型流程如图5 所示,主要分为原始数据处理、神经网络构建和模型训练及预测3 个部分。其中,原始数据处理采用归一化和MRMR 方法得到训练集和测试集。神经网络构建采用本文所提的基于DA-Seq2Seq 的城市能源负荷预测模型。最后,根据所选择的数据集和网络进行模型训练与测试,得到最终的城市能源系统电、热、冷负荷的预测结果。

图5 预测模型流程图Fig.5 Flow chart of forecasting model

4 算例分析

4.1 实验环境

本文实验均通过Python（版本3.6.10）实现,以PyTorch（版本1.7.1）作为深度学习框架。使用的计算机配置为Intel Core i5-10210U 1.60 GHz CPU,操作系统为Windows 10。

4.2 数据来源

本文选择的数据集为美国亚利桑那州立大学Campus Metabolism 项 目 网 站［37］2020 年1 月1 日 至2020 年12 月31 日的能源系统负荷数据和美国国家气象局网站［38］的气象数据,数据集为距离亚利桑那州立大学最近的数据点同时间段的气象序列,数据以1 h 为单位进行采样,每天采集24 个点,共8 784 个采集点。 输入序列分别由MIC 法和MRMR 方法选择,序列选择如表1 和表2 所示。

4.3 误差评价指标

选用下述指标对城市能源负荷预测的整体结果和峰值结果进行评价。

式 中:y͂i为 预 测 负 荷；yi为 实 际 负 荷；IRMSE和ISMAPE分别为预测结果的绝对误差和相对误差；IMASE为预测结果和天真预测结果之间的误差,其中天真预测［39］直接将前一天对应时刻的结果作为预测时刻的结果。IMASE值越小,说明预测效果越好,当IMASE值大于1 时,说明预测效果差于天真预测。

4.4 不同模型的预测结果

各深度学习模型的学习率设为0.001,步长T设为10,批大小设为256,迭代次数设为200 次,隐藏层的神经元数量为128,Seq2Seq 模型编码器和解码器的隐藏层神经元数量也设为128。

模型训练样本为2020 年1 月1 日至2020 年6 月15 日的数据,测试样本为6 月16 日至6 月29 日的数据。选取作为对比的模型包括差分整合移动平均自回 归（ARIMA）模 型、LSTM 网 络 模 型、CNNLSTM 模型、Seq2Seq 模型、注意力机制-LSTM（ALSTM）模型、MRMR-注意力机制-LSTM（MR-ALSTM）模 型、MRMR-DA-Seq2Seq（MR-A-DASeq2Seq）模型等。MR-A-LSTM 模型采用MRMR方法进行特征选取,输入序列如表2 所示,其他模型均采用MIC 法进行特征选择,输入序列如表1 所示。全部模型预测结果如表3 所示,其中,mmBTU 表示百万英热单位。图6 展示了以LSTM 网络模型和Seq2Seq 模型为基础的5 种模型后7 天的预测结果曲线。

图6 负荷预测结果Fig.6 Result of load forecasting

表3 不同模型的预测结果对比Table 3 Comparison of forecasting results with different models

首先,关注电、热、冷3 种能源负荷的MASE 按照2∶1∶1 的比例加权平均得到的wMASE 指标,可以通过对比天真预测反映预测方法的有效性。Seq2Seq 和ARIMA 模型预测结果的wMASE 指标分别为1.04 和1.70,均大于1,预测效果差于手动平移前一天负荷的天真预测方法,说明城市能源系统通过一般方法进行预测时难以学习到系统内的耦合关系,预测难度较大。LSTM、CNN-LSTM、ALSTM、DA-Seq2Seq 模型的wMASE 指标都在0.9附近,说明在单纯MIC 法的特征序列筛选下,上述负荷预测模型都不能实现有效预测,输入特征的选择对神经网络具有显著的影响。而MR-A-LSTM和MR-DA-Seq2Seq 模型的wMASE 指标都明显小于1,说明选择正确的特征输入后可以显著提升预测效果,而MR-A-LSTM 模型的wMASE 指标相较A-LSTM 模型降低了0.13,MR-DASeq2Seq 模型的wMASE 指标相较DA-Seq2Seq 模型降低了0.37,说明MRMR 指标的特征选择方法适用于Seq2Seq 模型,能够使其显著提高预测效果。

其次,关注电、热、冷3 种能源负荷的SMAPE按照2∶1∶1 的比例加权平均得到的wSMAPE 指标,可以反映预测模型的精度。对比所有模型可以看出,本文所提MR-DA-Seq2Seq 模型具有最好的测试效果,其平均相对误差相比A-LSTM 模型降低了1.32%,相比Seq2Seq 模型降低了2.27%,相比MR-A-LSTM 模型降低了0.67%。说明本文所提模型可在注意力机制和Seq2Seq 模型的基础上,提高城市能源多元负荷预测的精度。

具体到每一种负荷,可以看到电负荷预测中本文模型具有最好的效果,MR-A-LSTM 模型紧随其后,ARIMA 模型的预测效果很差,这是因为电负荷波动水平高,对输入特征依赖程度高,ARIMA 模型只能输入历史电负荷数据,所以预测精度最差。如图6（a）所示,90～95 h 时段内,本文所提MR-DASeq2Seq 模型贴合实际负荷曲线效果最好,交错在实际负荷之间,对负荷变化趋势掌握准确。而MRA-LSTM 模型的预测波动较大,说明可以学习到负荷变化的趋势但仍有缺陷,其他模型的预测结果都比较保守,精度不高。

热负荷预测中,众多预测模型精度区别不大,本文所提模型表现最好。由图6（b）中的热负荷预测结果可以看出,这段时间内热负荷的相对波动性非常强,而且没有明显规律,但波动的绝对值很小,这是因为所选时段为夏季,综合能源系统内具有热负荷需求的区域很少,热负荷需求变化受到的随机影响很多,但本文所提MR-DA-Seq2Seq 模型仍能学习到热负荷的波动规律,提高了热负荷预测的精度。

冷负荷需求的规律较为明显,整体波动性较小。 由 图6（c）可 以 看 出,本 文 所 提MR-DASeq2Seq 模型全程贴近实际负荷,在22～30 h 时段内距离实际负荷最近,在最后3 天内实际冷负荷向下波动时,也很好地预测了负荷的波动趋势,相比没有及时发现负荷下降的LSTM 模型,具有更好的表现。

同样模型架构下采用LSTM 网络建立神经网络模型时,应用注意力机制和MRMR 方法可以提升预测效果,但提升效果不够明显。而使用Seq2Seq模型作为基础的模型中,使用DA 机制后可以降低0.36%的平均相对误差,使用MRMR 方法后可以再降低1.84%的平均相对误差,说明MRMR 方法和DA 机制在Seq2Seq 模型上具有比较好的应用效果,能够更好地提取负荷特征信息,提升预测负荷的精度。

4.5 注意力机制在能源耦合关系上的体现

模型的训练集为2020 年1 月1 日至2020 年6 月22 日 的 数 据,测 试 集 为6 月23 日 至6 月29 日 的 数据。分别考虑如下4 种算法:

算法1:分别输入电、热、冷单一能源的数据,不考虑注意力机制,输出对应类型能源；

算法2:分别输入电、热、冷单一能源的数据,考虑注意力机制,输出对应类型能源；

算法3:同时输入电、热、冷能源数据和其他相关耦合信息,不考虑注意力机制,分别输出电、热、冷能源数据；

算法4:同时输入电、热、冷能源数据和其他相关耦合信息,并考虑注意力机制,分别输出电、热、冷能源数据,为本文采用的方法。

4 种算法的预测结果如表4 所示。

表4 不同算法的预测结果对比Table 4 Comparison of forecasting results with different algorithms

从表4 可以看出,同时输入多种能源并考虑注意力机制的算法4 效果最好。输入单一能源数据时,考虑注意力机制带来的提升不够明显,即算法2较算法1 的平均相对误差降低了0.50%,说明当输入信息不够充足,难以反映城市能源系统的能源耦合关系时,注意力机制发挥的作用有限,模型预测的精度也不够高。而在预测模型同时输入多种能源时,考虑注意力机制明显提升了精度,即算法4 的平均相对误差相比算法3 降低了1.90%,说明当信息密度充足时,DA 机制能够帮助神经网络学习到多种能源间的复杂耦合关系,从而提高城市能源系统多元负荷预测的精度。

4.6 预测算法的鲁棒性分析

1）不同季节数据间的对比

使用K均值聚类算法对每个季节的电、热、冷负荷进行聚类,得到一个聚类中心。然后,计算每天负荷同聚类中心的均方根并进行从小到大排序,平均排名最低的日期是同聚类中心最相似的日期,选择其作为典型日进行不同季节的负荷预测。

根据 上述方法选择2 月27 日、6 月23 日、9 月17日和11 月29 日分别作为4 个季节的典型日,该训练集选择典型日前60 天,预测模型使用A-LSTM 模型和MR-DA-Seq2Seq 模型。

不同季节的多元负荷预测结果如表5 所示,可以看到,常用的A-LSTM 模型预测精度在2%～10%波动,不能保持稳定的预测精度,而本文所提模型在每一个季度典型日的预测误差都能保持在3%左右,预测精度比较稳定。因此,本文所提模型具有足够的鲁棒性应对季节变化。

表5 不同季节的预测结果对比Table 5 Comparison of forecasting results in different seasons

2）气象预测误差的影响

模型训练样本为2020 年1 月1 日至2020 年6 月22 日的数据,评价指标为SMAPE,测试样本为6 月23 日至6 月29 日的数据。在模型训练完成后,调整测试数据的气象信息,在无气象误差的基础上,分别增加10%、20%、100%的随机误差,重新得到测试集结果,如表6 所示。预测模型使用A-LSTM 模型和MR-DA-Seq2Seq 模型。

表6 气象预测误差的影响Table 6 Impact of meteorological forecasting errors

城市能源系统中的电、热、冷负荷都会受到气象数据的影响,从表6 中可以看到,当气象数据误差为100% 时,预 测 模 型A-LSTM 和MR-DA-Seq2Seq的预测精度都有明显的下降。但是在城市能源系统的生产实践中,气象数据都是预测数据,预测误差不容忽视。因此,需要预测模型在面对气象预测误差时具有足够的鲁棒性。

本节分别考虑了输出气象数据存在0%～20%随机误差带来的影响,表6 中对比A-LSTM 和MRDA-Seq2Seq 模型可以看到,在应对气象误差时本文所提模型依然能够保持良好的预测效果,平均预测误差在“20%误差”时仅从2.8%上升到3.0%,说明本文所提模型具有足够的鲁棒性应对气象的变化。

5 结语

针对城市能源系统多元负荷短期预测问题,本文提出了一种基于MRMR 方法和DA 机制的预测方法。所提方法首先对输入序列特征进行处理,即无量纲化处理和基于MRMR 方法的特征序列选取；然后,输入DA-Seq2Seq 神经网络进行训练和预测,并在实际城市能源系统数据集上进行了仿真实验,得到如下结论:

1）相比已有负荷预测方法,所提基于DA 机制的城市能源系统多元负荷预测方法具有更好的预测精度。常用的A-LSTM 模型的平均误差为4.20%,而本文所提多元负荷预测技术的平均误差仅为2.88%,有效提高了城市能源系统多元负荷短期预测的精度。

2）DA 机制可以反映城市能源系统中的能源耦合关系,在多种能源负荷需求同时存在时,能更好地解决负荷预测问题。

3）MRMR 的相关性分析方法能有效筛选与城市能源负荷信息相关的特征序列,同时有效降低信息的冗余度,提升A-LSTM 模型和DA-Seq2Seq 模型的城市能源系统多元负荷预测精度。

4）不同季节和气象数据精度会对负荷预测的精度造成明显的影响,基于DA 机制的方法在不同季节和不同气象场景下都具有很高的预测精度,验证了本文所提方法的鲁棒性。

此外,本文所建立的基于MRMR 方法和DA 机制的城市能源多元负荷短期预测模型中可以加入多种能源的价格数据和城市能源系统的运行数据以提高预测精度,但受限于数据集中缺乏相关的信息,所以尚未在本文方法中考虑,在后续研究过程中可以进一步分析,以提高预测模型的精度。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。