含动态不确定性与频率电压控制的城市配电网灾后负荷恢复方法
林超凡,陈 晨,别朝红,李更丰
(1. 电力设备电气绝缘国家重点实验室,陕西省西安市 710049;2. 西安交通大学电力系统及其弹性研究所,陕西省西安市 710049)
0 引言
构建清洁低碳、安全高效的城市能源系统将有力支撑中国“双碳”目标的实现。然而,近年来频发的极端自然灾害对城市配电网的安全运行造成了威胁[1]。 同 时,大 量 分 布 式 新 能 源(distributed renewable energy source,DRES)、储能等分布式资源(distributed energy resource,DER)的接入增加了城市配电网的不确定性与控制复杂度[2],给灾后恢复带来了挑战。因此,研究考虑DER 运行特性的灾后恢复方法对保障“双碳”目标下的城市配电网安全运行十分重要。
城市配电网灾后恢复要尽可能地利用具有不确定性的DRES 以恢复更多的负荷。现有研究通常采用时序功率曲线(从历史数据中筛选[3]或预测工具得到[4])和预测误差概率分布描述DRES 和负荷的不确定性[5-6]。然而,在运行层面下,不确定因素的预测功率值及预测误差概率分布具有动态变化特性。同时,实际配电网中的DRES 和负荷难以在单个设备层面都配备预测工具[7],而数值天气预报也很难满足所需时空分辨率。为此,文献[7]提出了一种仅依靠历史数据和量测数据的DRES 出力概率分布的动态导出方法,并将其用于负荷恢复策略滚动求解,但没有考虑到配电网拓扑结构的影响,且采用的高斯混合模型精度受分量个数影响较大。
此外,城市配电网灾后恢复还需要考虑如何将配电网动态划分为多个微电网来提高孤网状态下的运行可靠性[8-9]。然而,与正常情况下由上游输电网提供支撑不同,灾后孤网状态下配电网划分成的多个微电网需要频率电压控制维持其安全稳定运行,但现有的灾后恢复文献未见相关内容。文献[10]将下垂控制DER 的静态频率电压特性考虑为解析约束,提出了微电网应对飓风的预防性措施优化模型,但没有计及DRES 等不确定因素的影响。此外,不同类型的负荷还对频率电压波动范围有不同的要求。文献[11]给出了电动机正常运行的频率范围为47.5~51.5 Hz,而照明、取暖等生活用电对频率波动要求较为宽松。因此,有必要将微电网频率电压控制以及不同负荷对频率电压的要求考虑进负荷恢复中,以保证恢复策略在实际配电网中的可行性。
针对上述问题,本文提出了一种含动态不确定性与频率电压控制的城市配电网灾后在线恢复方法。首先,基于C-Vine Copula 和条件概率对短期不确定性进行概率建模和场景生成,准确刻画运行层面下动态变化的不确定性。其次,建立了考虑频率电压约束的配电网灾后负荷恢复优化模型,并提出了一种高效的两阶段求解方法。最后,搭建了配电网在线恢复框架,根据当前DRES 和负荷的实时量测数据,对未来恢复策略进行滚动求解,在管控不确定性给配电网带来风险的同时最大化灾后可供电量,提升城市配电网的灾后恢复能力。
1 不确定因素动态概率建模及采样方法
本文采用C-Vine Copula 对多个随机变量进行概率建模,其优点主要有3 点:1)采用多样化的二元Copula 进行建模,灵活性更强、拟合精度更高[12];2)能根据当前时刻随机变量的数据,方便地导出条件概率分布并采样[13],生成短期时序场景;3)C-Vine Copula 更加适用于变量之间相关性较强的情形,且拟合和采样步骤较为简单[13]。
值得注意的是,本文的灾后恢复方法适用于发生频率较高、持续时间较短的常见极端事件,例如台风、暴雨、雷暴等,因此,可以认为灾后DRES 及负荷的不确定性与正常运行条件下相同,而与不同极端事件类型和强度无关。如果极端事件还未结束,则属于灾中响应范畴,需要针对不同极端事件对DRES 和负荷特性进行详细分析,本文不再赘述。
1.1 基于C-Vine Copula 的离线概率建模
C-Vine Copula 概率密度函数(probability density function,PDF)fJ(∙)可表示为:
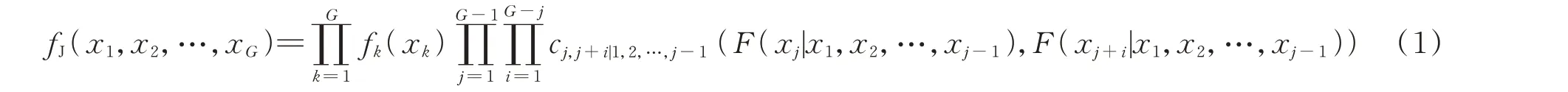
式中:x1、x2、…、xG为G个随机变量;fk(xk)为第k个随机变量的PDF,本文采用非参数核密度估计(kernel density estimation,KDE)[14]对其进行拟合;F(xj|x1,x2,…,xj-1)为第j个随机变量xj关于随机变量x1至xj-1的条件累积分布函数(cumulative distribution function,CDF);cj,j+i|1,2,…,j-1(∙)为 相 应的二元条件Copula 函数,可通过拟合优度检验确定最优Copula 类型[12]。
本文的重点不是概率建模,因此直接选择二元高斯Copula 进行建模,其表达式为:
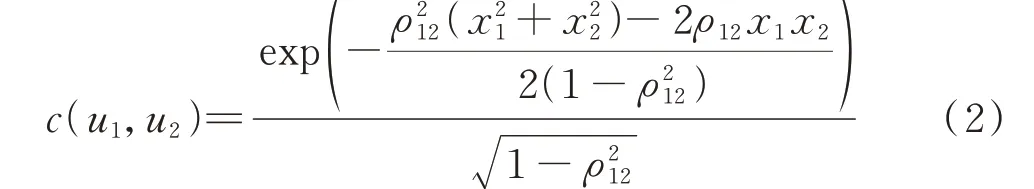
式中:u1和u2分别为在[0,1]区间上的连续变量;ρ12为描述相关性的高斯Copula 参数;x1和x2分别为Φ-1(u1)和Φ-1(u2),其中,Φ(∙)为标准正态分布CDF。
为了解决配电网单个DRES 或负荷层面缺少预测工具的问题,本文离线概率建模的对象是G个DRES 出力或负荷的当前时刻状态和未来时刻状态,共计2G个随机变量。首先,将G个DRES 出力或负荷的历史数据按处于一天中的时刻划分为多个子集(若数据精度为小时,则有24 个子集)。然后,对每个子集中每个DRES 出力或负荷的数据进行KDE 估计,获取经验CDF 和PDF。最后,对所有相邻子集的2G个随机变量历史数据进行相关性建模,即通过参数估计获得式(1)中每个二元Copula的相关性参数[13]。
1.2 基于条件概率的在线时序场景生成法
实际配电网运行时,根据当前时刻G个DRES出力或负荷的实测值,可依次导出下一时刻每个随机变量的条件CDF,按逆分布进行采样,表达式为:

式中:w1,w2,…,wG为[0,1]区间上独立生成的随机数;yc为当前时刻实测值G维向量;F-1(∙)为逆CDF。
C-Vine Copula 由于运算只涉及二元变量,其条件CDF 具有解析表达式,且采样过程非常简单[13],极大方便了场景生成。其步骤如下:
步骤1:给定时序场景时刻数H(与后续多时段优化的时间窗长度一致)和采样场景数L(为保障场景的完备性一般为一个较大值),并设置初始时刻τ=1 和初始场景数γ=1,令当前时刻DRES 的出力或负荷值x为实时量测值x0,且x=x0。
步骤2:根据式(3)采样得到下一时刻DRES 出力或负荷的一个采样值yτ,并令τ=τ+1。
步骤3:若τ≤H,则令当前时刻DRES 的出力或负荷值x=yτ,返回步骤2,否则继续执行。
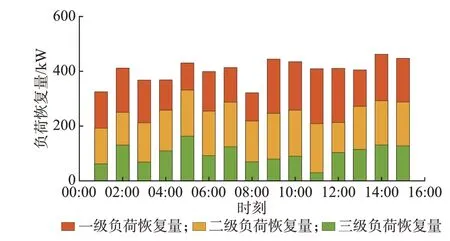
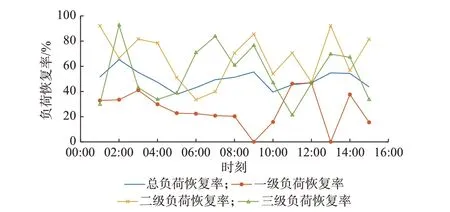
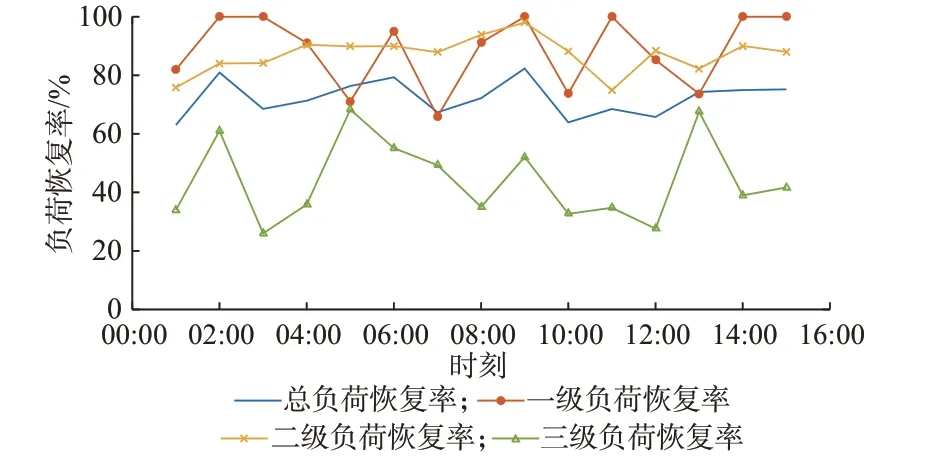
步骤4:拼接所有采样值yτ,τ=1,2,…,H便形成了所有DRES 出力或负荷的一个时序场景。若γ 场景生成后,大量的时序场景会增加后续随机优化的计算量。因此,可以通过一定的场景削减方法,例如K-means 算法筛选出最能保持原有场景特性的少量典型代表性场景[15],以减少后续计算量。 配电网在正常情况下,其频率和电压由上游输电网提供支撑,接入的DER 通常不参与频率和电压调节,而仅具有功率注入功能即可。但是,在受到极端自然灾害袭击后,很可能由于馈线断线或者输电网断电而处于孤岛运行模式,并形成多个由不同DER 供电的微电网[16]。此时,每个孤网均需要至少有一个DER 具备频率电压控制能力,负责该微电网的频率电压稳定[17]。由于配电网灾后受损情况已知,未受损部分的运行与一般情况下的孤网运行并无区别,可以沿用相关的孤岛微电网控制方法。下垂控制作为最常见的控制模式之一,被广泛应用在孤 岛 微 电 网 的 潮 流 计 算[18]、孤 岛 检 测[19]、优 化 运行[20]等研究。由于不需要DER 之间的通信[21],非常适合灾后通信受损情况下的孤岛微电网控制和负荷恢复[17]。其控制结构如附录A 图A1 所示,输出特性为: 式中:P和Q分别为DER 有功出力和无功出力;P*和Q*分别为DER 有功出力和无功出力的参考值;f和V分别为出口端的频率和电压;f*和V*分别为出口端频率和电压的参考值;KP和KQ分别为有功功率-频率和无功功率-电压下垂系数。 与传统配电网黑启动的次序恢复概念[22]不同,本文所涉及的灾后恢复旨在通过稳态优化调整DER 出力、控制负荷开断、调整微电网划分结构,来实现孤岛状态下的城市配电网灾后供电负荷最大化[17,23]。值得注意的是,配电网灾后恢复通常都基于已知的系统状态进行分析[4-8,16-17,22-23],因为灾后极端事件的影响已经确定,相应的优化模型和决策方法是通用的。 灾后负荷恢复优化的目标函数为: 式中:d∈ND为接入下垂控制DER 的节点集合ND的元素;dˉ∈NND为未接入下垂控制DER 的节点集合NND的元素;m为首端节点为n的线路的末端节点;αnm,t为t时刻节点n和m之间线路状态(αnm,t=1表示t时刻线路闭合,αnm,t=0 表示t时刻线路断开);βnm,t为t时刻节点n和m之间线路两端节点的父子连接关系(βnm,t=1 表示t时刻节点m是节点n的父节点,反之则βnm,t=0)。 2)多种类型的DER 运行约束 对于接入DRES 的PQ节点,其接入的DRES通常运行在最大功率点处[24],以保证对新能源的最大化利用,且有功功率和无功功率之间保持恒定的功率系数[25],以满足配电网并网要求,表达式为: 式中:e∈NE为接入储能节点集合NE的元素;Pe,t,Ech和Pe,t,Edis分别为节点e处储能在t时刻的充电功率和放电功率;Pe,Emax为额定充放电功率;xe,t,Ech和xe,t,Edis分别为节点e处储能在t时刻充电和放电状态的0-1 决策变量;ηe,ch和ηe,dis分别为充电效率和放电效率;Se,t,E为节点e处储能在t时刻的荷电状态;Se,Emin和Se,Emax分别为节点e处储能荷电状态的最小值和最大值。 对于接入下垂控制DER 的Vf节点,根据式(4)和式(5)可得到约束为: 式中:Pd,t,Dref和Qd,t,Dref分别为节点d处下垂控制DER 在t时刻给定的有功出力和无功出力的参考值;Ps,d,t,D和Qs,d,t,D分别为t时刻节点d处下垂控制DER 在特定场景s下的实际有功出力和无功出力;fref为系统额定频率;Ud,ref为节点d的参考电压;fs,d,t和Us,d,t分别为t时刻节点d在场景s下的频率和电压幅值;Kd,DP和Kd,DQ分别为节点d处下垂控制DER 的有功频率-频率和无功频率-电压下垂系数。 同时,功率参考值和实际值应满足范围为: 式中:l为末端节点为n的线路的首端节点;Ps,nm,t和Qs,nm,t分别为t时刻场景s下从节点n流向节点m的线路有功功率和无功功率;Ps,ln,t和Qs,ln,t分别为t时刻和场景s下从节点l流向节点n的线路有功功率和无功功率;Ps,n,t和Qs,n,t分别为节点n注入的有功功率和无功功率。 Ps,n,t和Qs,n,t的 表 达 式 为: 4)安全约束 在负荷恢复过程中,如果某个节点上的负荷被恢复,则该节点的频率和电压应该在其安全范围内,表达式为: 式中:Pnm,min和Pnm,max分别为节点n和m之间线路所允许流过的有功功率的最小值和最大值;Qnm,min和Qnm,max分别为该线路所允许流过的无功功率的最小值和最大值。 3.1 节中的优化模型为典型的混合整数线性规划模型,可调用CPLEX、Gurobi、MOSEK 等商业求解器进行求解。该优化模型具有较多整数变量,求解效率低,因此,本文将其转化为两阶段求解: 1)第1 阶段:以长时间尺度(例如5 h)为周期,求解未来多个时间段的负荷恢复策略,得到相应的动态微电网拓扑结构。目标函数为式(6),约束条件为式(7)至式(33)。 2)第2 阶段:基于固定微电网拓扑,以短时间尺度(例如1 h)为周期,快速求解未来多个时间段的负荷恢复策略,确定最终恢复结果和系统状态。目标函数为式(6),约束条件为式(10)至式(34)所示。 式中:αnm,t,I为第1 阶段求解得到的拓扑变量值。 值得一提的是,在两阶段优化下,长时间尺度负荷恢复策略被短时间尺度优化修正后依然是可行的。这是由于长时间尺度的优化实际上只提供了动态微电网划分的边界条件,而短时间尺度的优化在任意微电网拓扑下均能找到负荷恢复的可行解,只是最优性会有所降低(将在算例5.4 节中说明)。 对于实时调度中的每一决策时刻,首先,获得多个DRES 出力和负荷的实时量测数据,通过式(3)采样生成未来一段时间DRES 出力和负荷的时序场景。其次,根据第3 章中的负荷恢复优化模型及其两阶段求解方法求解最优负荷恢复策略。最后,仅实施下一时段的恢复策略。因为在下一实时调度的决策时刻又会有新的量测数据,不确定场景及恢复策略也会相应更新。整个灾后在线负荷恢复流程图如附录A 图A2 所示。 相较于传统模型,本文通过将频率和电压变量纳入决策优化,实现了频率电压控制和负荷恢复优化的协调配合。此外,对于本文小时级时间尺度的负荷恢复来说,下垂控制在秒级时间尺度的响应可以忽略不计,因为负荷恢复面向的是稳态优化运行决策而非暂态频率电压控制[17]。 本文所提城市配电网灾后在线负荷恢复框架在改进的IEEE 37 节点馈线测试系统上进行验证,其拓扑如附录B 图B1 所示。系统各个节点负荷功率大小及其权重均取自文献[8]。负荷类型按权重划分为一级、二级、三级负荷[17],对应的频率和电压允许波动范围参考文献[17]。支路的数据由测试系统原始文档[26]导出。测试系统中接入了众多DER,其接入位置如附录B 图B1 所示。其中,只有4 台微型燃气轮机配置有下垂控制,负责对应微电网的频率电压控制,而其他DER 均工作在PQ模式。DER 的主要参数如附录C 表C1 所示。分布式光伏和风机、负荷的原始数据均取自欧洲电网透明平台ENTSOE[27],且按照算例中分布式光伏、风机和负荷的额定容量进行放缩。 假设受极端天气影响,该测试系统与上游输电网在01:00 至15:00 断开而孤岛运行,采用本文所提方法进行灾后恢复。在线时序场景生成的时刻个数设置为5,采样场景数设置为100,采用K-means 算法进行场景削减,保留5 个典型场景。两阶段优化中的拓扑决策周期设置为5 h,负荷恢复决策周期设置为1 h,时间分辨率为1 h,优化窗为5 h。每次优化的停止判定条件为差距值小于0.1% 或计算时长超过45 min。 为了展示负荷恢复情况,对每个时刻不同类型负荷定义的指标表达式为: 式中:At和Rt分别为t时刻的负荷恢复量和负荷恢复率;Pn,t,realL为节点n在t时刻真实的负荷有功功率值;Ns为任意节点集合。 在恢复过程中,指标的变化情况如图1 和图2所示。需要注意的是,图1 和图2 以及后续时序恢复相关的图是每个时段实施完决策后统计得到的指标,而不是一次优化决策的结果展示。 图1 负荷恢复量指标变化情况Fig.1 Variation situation of load restoration amount index 图2 负荷恢复率指标变化情况Fig.2 Variation situation of load restoration ratio index 由图1 和图2 可知,各级负荷的恢复水平随时间变化较大,这主要是由动态微电网划分导致的,同时也受动态变化的DRES 和负荷不确定性影响。图1 中,白天时段的负荷总体恢复量要大于晚上时段,说明了分布式光伏对提升城市配电网负荷恢复能力的作用。从图2 可以看出,一级负荷恢复率平均值略大于二级负荷,且两者负荷恢复率整体水平都要明显高于三级负荷,说明本文所提方法会优先恢复更重要的负荷,符合实际配电网需求。 恢复过程中2 个不同时刻的动态微电网划分结构如附录B 图B2 所示。计算可知,若将07:00 的拓扑应用于14:00,则14:00 的总体负荷恢复率和一级负荷恢复率将分别降低至77.82%和87.98%;若将14:00 的拓扑应用于07:00,则07:00 的总体负荷恢复率和一级负荷恢复率将分别降低至71.32% 和54.47%。因此,相比固定微电网边界,本文动态微电网结构能随着DRES 出力和负荷的变化而变化,从而利用有限的DER 在更大程度上恢复负荷。 首先,为了验证C-Vine Copula 的准确性,将其与2 种 传 统Copula 模 型Gaussian-Copula 和t-Copula进行对比。定义两类指标表达式为: 式 中:bz为 点z处 的CDF 距 离;Cem(∙)为 经 验CDF,可 通 过 历 史 数 据 得 到;C(∙)为3 种Copula 模 型 的CDF;Z为样本点个数;bˉ为样本点平均距离,可用于衡量概率模型对于原始样本数据的拟合效果。 此处,以3 个分布式风机出力概率建模为例进行 说 明,在07:00 与07:15 时,不 同 类 型Copula 模 型在相同100 个样本点下的距离如附录B 图B3(a)所示,在全天96 个时刻与紧接未来时刻不同类型Copula 模型的样本点平均距离如图B3(b)所示。图中,距离指标平均值及每个模型所需的平均建模时间如附录C 表C2 所示。 由附录B 图B3 可知,对于单个概率模型的不同样本点来说,3 种Copula 模型计算CDF 的误差会有所变化,但总体来说,C-Vine Copula 精度要大于t-Copula 和Gaussian-Copula。对于一天内的所有概率模型来说,情况也类似,部分时刻概率模型可能出现t-Copula 精度略高于C-Vine Copula 的情况,但这2 类模型的精度始终高于Gaussian-Copula。此外,C-Vine Copula 在计算时间上还具有显著优势,单个模型建模所用平均时间仅为t-Copula 的1.5%。 其次,将本文所提动态概率建模及采样方法与传统蒙特卡洛采样方法进行对比。在某日10:00时,通过2 种方法采样得到的时序场景如附录B 图B4 所示。可知,2 种方法采样出来的时序场景均能覆盖真实场景,并且趋势一致。本文所提方法能显著缩小生成场景的不确定性,为后续随机优化提供更加准确可靠的场景集合,减少不确定性对优化结果和恢复决策的影响。 若采用传统方法所生成的场景进行随机优化,则负荷恢复过程中负荷恢复率指标的变化情况如图3 所示。对比图3 和图2 可知,若采用传统方法生成的场景进行优化,则总体、一级、二级负荷恢复率均有所下降,尤其是一级负荷恢复率平均值由83.39%降至25.69%,三级负荷恢复率有所提高。 图3 不考虑动态不确定性的负荷恢复率指标变化情况Fig.3 Variation situation of load restoration ratio index without considering dynamic uncertainty 图3 现象产生的原因是:当不考虑运行层面下动态变化的不确定性时,生成的短期时序场景会高估系统可能出现的不确定性,从而造成负荷恢复策略过于保守。2 种方法下得到的场景在各个时刻的不平衡功率波动范围如附录B 图B5 所示。3 种类型负荷根据下垂系数折算的系统最大可接受不平衡功率波动分别为5、100、500 kW。由图B5 可知,传统方法生成场景的功率波动要明显大于所提方法生成的场景。在13:00 时,传统方法生成场景的功率波动甚至超过100 kW,即使所有负荷均为二级负荷,依然有部分负荷无法恢复,频率要求更严苛的一级负荷则更难以恢复,图3 中该时刻一级负荷恢复量为0。相比之下,所提方法生成场景的功率波动基本在10 kW 以内,能恢复更多一级负荷。因此,在线负荷恢复中考虑动态不确定性将有助于提高城市配电网灾后负荷恢复能力。 为验证频率电压控制及负荷差异化频率电压特性对负荷恢复结果的影响,采用无下垂控制和频率电压特性约束的优化模型进行优化,恢复过程中负荷恢复率指标变化情况如图4 所示。 图4 不考虑频率电压控制的负荷恢复率指标变化情况Fig.4 Variation situation of load restoration ratio index without considering frequency-voltage regulation 对比图4 和图2 可知,若不考虑频率电压控制以及负荷对频率电压的差异化要求,则负荷将严格按照重要度进行恢复。其中,一级负荷全部恢复,二级负荷约90%恢复。然而,实际城市配电网中由于负荷的差异化特性,部分微电网中的少量重要负荷由于对频率电压要求严苛而放弃恢复,转而恢复更多的对频率电压要求宽松的非重要负荷。因此,需要在优化模型中考虑到频率和电压的相关约束,才能使得求解得到的恢复策略在实际配电网中可行。 为验证本文所提两阶段优化方法的有效性,将拓扑决策周期从5 h 调整为1 h(即单阶段优化),相应负荷恢复率指标变化情况如图5 所示。 图5 不考虑两阶段优化的负荷恢复率指标变化情况Fig.5 Variation situation of load restoration ratio index without considering two-stage optimization 对比图5 和图2 可知,2 种算法得到的负荷恢复情况非常相似,两阶段优化算法相对于单阶段优化,总负荷恢复率平均值仅下降了2.31%,各类型负荷恢复率平均值也较为接近。进一步比较2 种优化的目标函数值和计算时间,作为计算精度和效率的衡量指标,如附录C 表C3 所示。可知,在两阶段算法下,每5 h 才进行1 次耗时的长时间尺度优化确定拓扑,每1 h 只进行快速的负荷恢复决策,计算效率提高了约4 倍,但目标函数值仅下降了4.01%,从而验证了本文所提两阶段优化能够在保证求解精度的同时,提升了优化的总体效率。 本文综合考虑运行层面动态变化的不确定性、动态微电网划分、频率电压下垂控制以及负荷对频率电压的不同要求,提出了城市配电网的灾后在线负荷恢复决策方法。得到的主要结论如下: 1)本文基于C-Vine Copula 的离线概率建模及在线场景生成方法能准确刻画运行层面下DRES 出力及负荷的动态不确定性,提高随机优化场景的可靠性,进而提高城市配电网灾后恢复能力。 2)通过在优化模型中引入动态微电网划分能根据DRES 出力和负荷的变化调整微电网边界,更大程度上利用了有限的DER,进一步提高了负荷恢复率。 3)微电网频率电压控制以及不同负荷对频率电压的差异性要求会使得部分约束宽松的非重要负荷代替部分约束严格的重要负荷恢复,必须考虑进优化模型才能得到实际配电网可行的恢复策略。 4)两阶段优化求解方法能在保证求解精度的同时显著提高求解效率,满足在线负荷恢复的要求。 未来将进一步研究所提配电网灾后恢复方法与灾后元件修复的协同优化。此外,由于一些发生频率低、影响范围大的非常规极端事件,例如地震、山火、极寒、极热等,会对灾后DRES 及负荷特性具有较大影响,后续考虑针对这些极端事件的不同特性进行更深入细致的探索。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。2 孤网频率电压控制原理
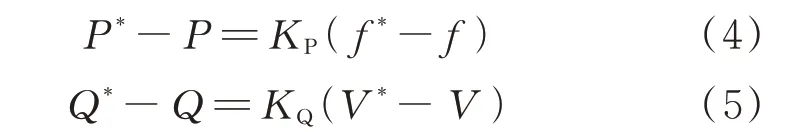
3 配电网灾后负荷恢复两阶段优化模型
3.1 灾后负荷恢复原始优化模型






3.2 优化模型的两阶段求解算法

4 灾后在线负荷恢复框架
5 算例分析
5.1 负荷恢复结果展示
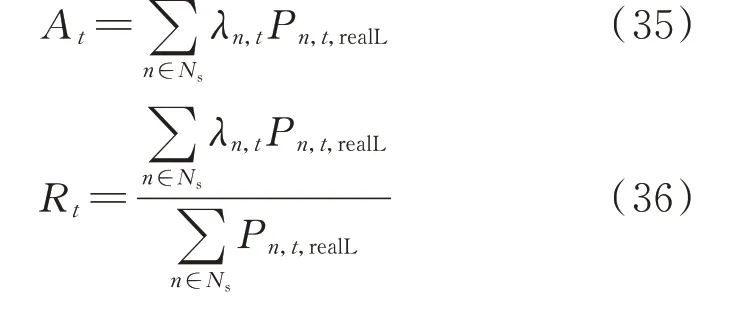

5.2 对比验证1:概率建模及场景生成方法
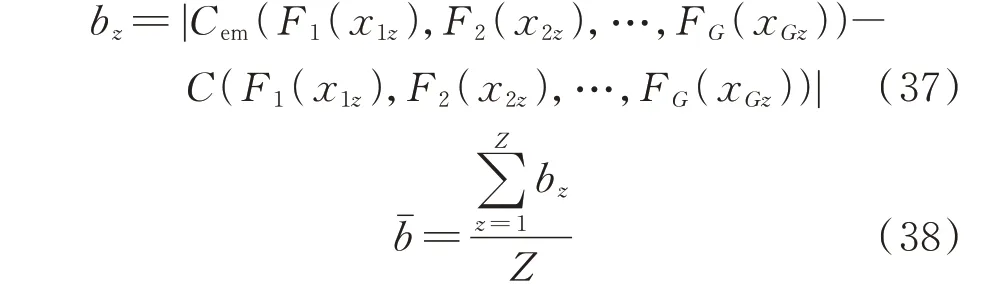
5.3 对比验证2:频率电压控制及负荷差异化特性

5.4 对比验证3:两阶段优化方法
6 结语

