无人机集群打击海面目标指定时间协同控制方法
冯 政, 吴 傲, 王谦喆
(1.空军工程大学空管领航学院,西安 710000; 2.陕西省电子信息系统综合集成重点实验室,西安 710000)
0 引言
对于入侵我方领海的以中小型海面舰艇为代表的敌方海面目标,可采用无人机集群来打击。一是因为该类目标体积大、价值高、机动性差,是合适的“靶目标”;二是因为舰载防空系统主要是针对各类反舰导弹和飞机,应对“低慢小”目标能力有限[1]。无人机集群利用数量多、雷达红外特征弱的特点,携带多种类型的武器弹药,从多个方向对水面舰艇实施饱和攻击[2],将对敌方高价值目标造成巨大威胁。
随着未来作战模式逐渐向协同化转变,无人机协同作战相关技术已成为目前的研究热点[3]。本文重点研究协同打击中的时空协同问题。精准的时空耦合是集群发挥协同优势的关键,从系统控制角度看,可将其视为带时间参数的群系统编队控制问题。
编队控制方面的研究成果包括有限时间控制[4]、固定时间控制[5-9]以及指定时间控制[10]。有限时间控制中,系统在有限时间收敛,但收敛时间上界与系统的初始状态有关。固定时间控制中收敛时间上界不受初始条件影响,只与参数有关[11];但是,由于固定时间控制的收敛时间与控制参数有着复杂的耦合关系,繁琐的多调参变量和函数关系限制了固定时间控制法在集群控制中的应用[12];与固定时间控制相比,指定时间控制要求收敛时间能独立输入且自由预置,具有更大的应用潜力。文献[13]提出了指定时间一致性问题,研究了多智能体线性系统指定时间控制,系统可以根据任务要求离线预置收敛时间,但是系统的期望状态是非时变的;文献[14]研究了多智能体系统的指定时间编队控制问题,但其指定时间仍然是上限。
本文以指定时间协同控制方法为支撑,主要解决集群指定时间和指定时长协同打击问题。
1 无人机集群对海目标指定时间协同打击问题模型
无人机集群对海上目标发起协同打击指定时间构型控制包含两个控制目标。
1) 构型生成。无人机集群在指定的打击时刻tf生成打击构型,同时对目标发起饱和打击。
2) 构型保持。无人机集群生成打击构型后在指定的时间段te内保持打击构型,持续对目标发起打击,如图1所示。

图1 无人机集群指定时间协同打击构型控制示意图Fig.1 Configuration control diagram of UAV swarm for cooperative attacking at designated time
用Ui表示编队中编号为i的无人机,其中,i=0,1,2,…,n,U0表示海面目标。令epi(t)=[epix(t),epiy(t),epiz(t)]T∈R3,evi(t)=[evix(t),eviy(t),eviz(t)]T∈R3及eui(t)=[euix(t),euiy(t),euiz(t)]T∈R3分别表示惯性系(北东地坐标系)中Ui的位置状态、速度状态及加速度状态。接下来定义Ui的状态向量为exi(t)=[epix(t),evix(t),epiy(t),eviy(t),epiz(t),eviz(t)]T∈R6。
为了描述无人机群所期望的时变编队,将每架无人机与海面目标的相对状态ef(t)定义为惯性坐标系下的编队参数向量,有
ef(t)=[ef0(t),ef1(t),…,efn(t)]T
(1)
其中,对于i=0,1,2,…,n有
efi(t)=exi(t)-ex0(t)
(2)
efi(t)=[efix(t),efiy(t),efiz(t)]T
(3)
efix(t)=[efixp(t),efixv(t)]T
(4)
efiy(t)=[efiyp(t),efiyv(t)]T
(5)
efiz(t)=[efizp(t),efizv(t)]T
(6)
efi(t)反映了达成期望构型时Ui与海面目标的期望位置差与速度差,易得ef0(t)=0。那么,编队中Ui与Uj之间期望的相对状态可以用Δefi j(t)∈R6来表示,即
Δefi j(t)=efi(t)-efj(t)。
(7)
定义1对于tf,te两个时间参数,无人机集群达成了指定时间构型控制,当且仅当对于i,j∈0,1,2,…,n,Ui与Uj满足下列两个条件:
1) 构型生成条件
(8)
2) 构型保持条件
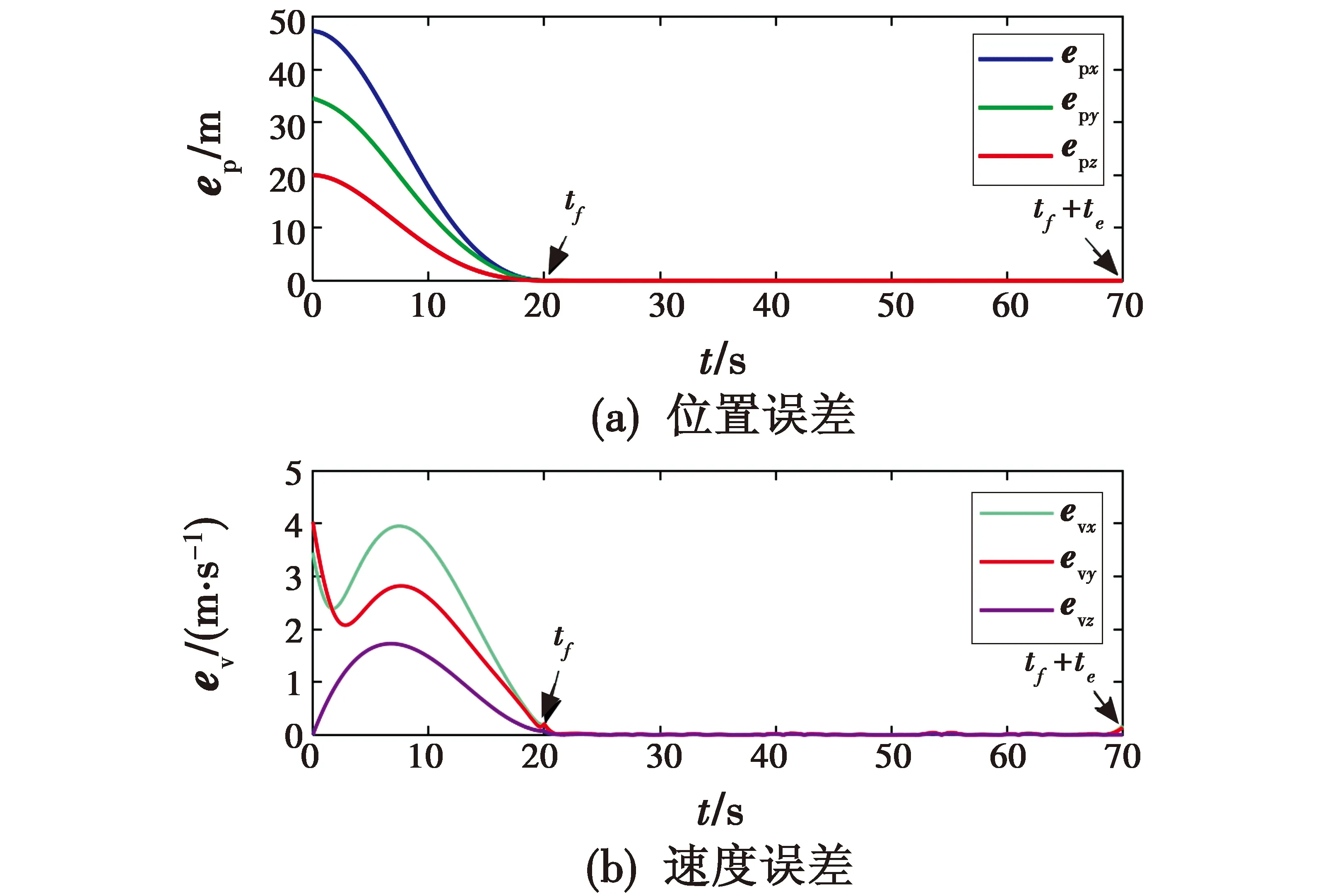
exi(t)-exj(t)≡Δefi j(t)tf (9) 指定时间编队控制器将被设计用于实现定义1的控制目标,控制模型如图2所示。 图2 无人机控制模型Fig.2 Control model of UAV 图2中:外环为编队协同控制层,负责根据期望构型、参考航迹和速度等邻居个体的状态信息,计算本机的期望姿态角;内环控制根据外环得到的控制输入,结合自身动力学特性计算期望控制量,对本机油门、电机转速等进行控制,实现期望的姿态。在外环控制层,可将无人机视为一个质点,其运动方程可用二阶积分器描述为 (10) (11) (12) 式中,ai j根据通信邻接关系取值为0或1。 根据无人机动力学模型,无人机间的相对状态满足 (13) (14) (15) 令X(t)∈R6(n+1),U(t)∈R6(n+1)及Y(t)∈R6(n+1)分别代表系统的状态向量、输入向量和输出向量,即 X(t)=[ex0(t),ex1(t),…,exn(t)] (16) U(t)=[eu0(t),eu1(t),…,eun(t)] (17) (18) 那么系统的状态空间方程可表示为 (19) (20) e(t)=Yd(t)-Y(t)。 (21) 定义1中的两个条件用e(t)来表示,转化为 1) 构型生成条件 (22) 2) 构型保持条件 e(t)≡0tf (23) 为实现指定时间的构型控制,将最优控制理论中的有限时间时变最优跟踪器引入编队控制系统。二次代价函数的一般形式为 (24) 式中:t0和t1分别表示指定的初始和末端时刻;F∈R6(n+1)×6(n+1),是一个表示末端时刻误差代价的对称非负时不变矩阵;Q(t)∈R6(n+1)×6(n+1)和R(t)∈R6(n+1)×6(n+1)均为对称正定时变矩阵,分别代表控制过程中实时的误差代价和控制代价,是连续的,并且在区间t∈[t0,t1]内有界。 设计二次代价函数中的F,Q(t)和R(t)。考虑到空间3个维度方向上的位置误差和速度误差是等权重的,因此,F选择单位矩阵,即 F=I6(n+1)。 (25) 然而,对于不同的控制阶段,控制目标是不同的,因此Q(t)和R(t)也是不同的。 1) 构型生成阶段t∈[0,tf]。 t0=0,t1=tf,要求系统在末端时刻tf生成期望的编队构型。R(t)反映的是整个控制过程中实时的控制代价,在构型生成阶段关注的是末端时刻构型的生成,因此,越接近末端时刻tf控制代价应该越大。这意味着在初始阶段有较大的控制输入使得期望构型能够更快速地生成,并且随着时间的增长,控制输入应该逐渐减少,直至t=tf时减少到0。因此在构型生成阶段,设计R(t)为 (26) 构型生成阶段仅关注末端时刻tf的控制误差,不关注过程中的构型误差,因此设计Q(t)为 Q(t)=0。 (27) 2) 构型保持阶段t∈(tf,tf+te]。 t0=tf,t1=tf+te,要求系统在t∈(tf,tf+te]时间段内一直保持期望的时变编队构型。由于该阶段关注的是整个控制过程,所以过程误差应该尽可能小。除此之外,控制误差和控制代价在构型保持时间段内都应该是等价的,因此,Q(t)和R(t)在该阶段均被设计为单位矩阵,即 R(t)=I6(n+1) (28) Q(t)=I6(n+1)。 (29) 对于最优控制理论中的有限时间跟踪系统,如果矩阵对{A,C}是完全可观的,那么对于二次代价函数式(24)必有唯一的最优控制,即 U*(t)=-R-1(t)BT[P(t)X(t)-g(t)] (30) (31) Riccati方程的末端约束为 P(t1)=CTFC (32) Riccati方程中的g(t)∈R6(n+1)是满足如下向量微分方程的伴随向量,即 (33) 向量微分方程的末端约束为 g(t1)=CTFYd(t1) (34) 根据式(31)和式(32)可知,P(t)的求解是独立于系统的期望输出与初始状态的,因此对于t∈[t0,t1]的P(t)可以事先离线求解。Yd(t)代表了集群的期望构型,对于控制器而言是已知的。因此,伴随向量g(t)可基于边界条件式(34)得到 (35) 其中,t∈[t0,t1],Ψ(t,t0)为式(33)的状态转移矩阵。 已知P(t)和g(t)可得U*(t),将U*(t)代入系统的开环状态方程式(19)即可得到系统的闭环状态方程为 (36) 式(36)的边界条件为 X(t0)=X0。 (37) (38) 采用Matlab模拟无人机集群打击海上动态目标。 场景设为5架无人机打击海面目标。设海面目标编号U0,无人机编号为Ui,i=1,2,…,5。无人机初始横坐标为 epix(0)=5i-10 (39) 无人机其余初始状态参数均为零。 为实现对海面目标的全向饱和打击,同时增加自身防御,设置期望的编队构型为半径r=10 m,旋转角速度ω=0.1 rad/s的圆周构型。构型参数为 (40) 定义位置误差向量ep(t)∈R3和速度误差向量ev(t)∈R3 (41) (42) 设海面目标U0的初始状态向量为ex0(0)=[01 0100]T,当t∈(0,10]∪(20,50]∪(60,70](单位为s)时,海面目标保持速度为1.5 m/s的匀速直线运动;当t∈(10,20](单位为s)时,海面目标按照ω0(t)=-π/20 rad/s的角速度匀速右转弯;当t∈(50,60]时,海面目标按照ω0(t)=π/30 rad/s的角速度匀速左转弯。 时间参数可设为无人机群20 s时在目标上空形成打击构型,发起时长为50 s的打击。 采用上文设计的控制律,集群编队的仿真轨迹见图3。 图3 无人机集群对动目标打击轨迹俯视图Fig.3 Top view of attack trajectory of UAV swarm against moving target 无人机集群成功地在t=20 s时生成了期望的打击构型,并且在接下来的50 s时间段内稳定地保持打击构型,同时跟踪海面目标运动。 图4则展示了打击过程中的位置误差和速度误差,在构型生成时刻误差正好收敛到向量0,在构型保持阶段误差持续稳定在向量0附近。 图4 无人机集群位置误差和速度误差曲线Fig.4 Curve of position error and velocity error of UAV swarm 仿真实验结果证明,在指定的时间参数下,无人机集群能够成功地生成并保持期望的编队构型,对动态目标能够实现跟踪。值得注意的是,图4所示的误差曲线与式(22)和式(23)中的控制目标是一致的。编队误差恰好在tf时刻收敛到向量0,说明tf是精准的构型生成时刻,并且是独立的系统输入,不受控制器参数的影响,这极大地提高了集群控制的灵活性。 本文所提的方法可以驱动无人机群在指定的时刻精准地生成打击构型,实现“同时到达”的打击策略,并在后续指定时段内保持打击构型,实现持续打击。下一步工作可以采取无人机集群实飞来验证。2 指定时间协同控制律设计及求解
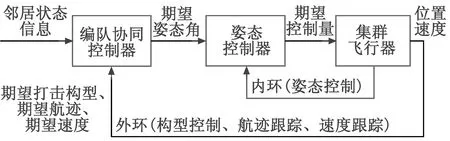
2.1 集群编队控制系统描述
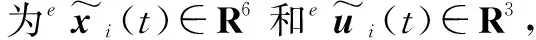
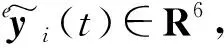
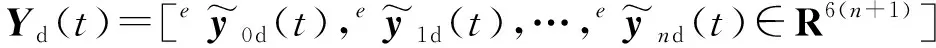
2.2 最优控制二次代价函数设计
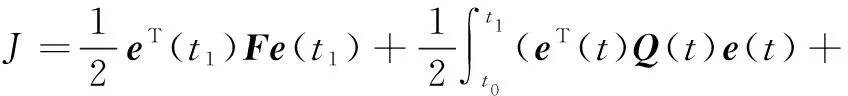
2.3 基于龙格库塔法的控制律求解
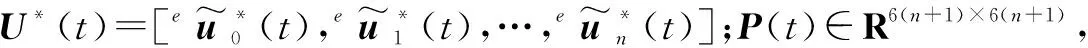
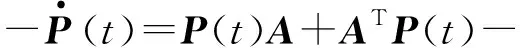

3 仿真分析
3.1 仿真参数设置
3.2 仿真结果
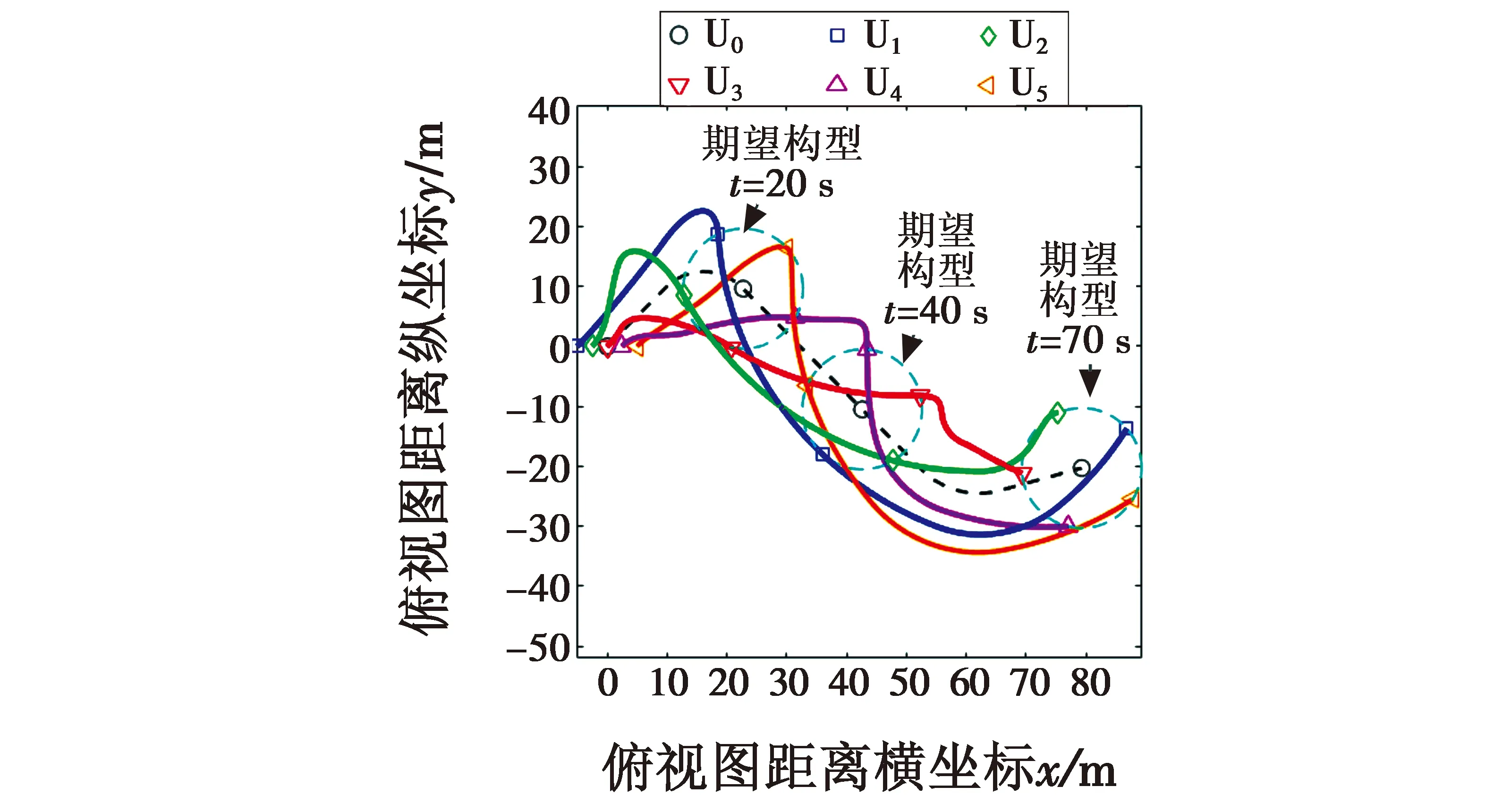
4 结论

