考虑目标主动防御的空地弹药微分对策制导

李俊贤， 范军芳

(北京信息科技大学高动态导航技术北京市重点实验室，北京 100000)

0 引言

近年来的局部冲突、城市巷战及2020年纳卡冲突等实践均表明，攻防各方的信息化与智能化水平显著提升，攻击弹药、目标以及目标发射的防卫弹药在攻防对抗中符合智能体的内涵。局部环境中导弹与目标之间、防御弹和攻击弹之间的博弈研究具有重要的理论与实际价值。

文献[1]应用强化学习的方法求解微分对策的问题；文献[2]基于单神经网络的策略迭代算法实现了对微小卫星微分博弈均衡策略的逼近，但该算法计算复杂度高；文献[3]针对目标可以对攻击弹进行主动防御的问题，设计了攻击弹拦截主动防御目标的微分对策制导律；文献[4]针对飞行器逃避拦截器追踪的问题，提出了基于最优控制的目标和防御弹协同躲避和追击的策略，但是该制导律的实施需要已知来袭攻击弹的制导律，不符合实际情况；文献[5]针对攻防双方分别设计了最优规避策略和突防策略；文献[6-7]考虑了交战模型中的非线性情况，但是各方的控制方式较简单，未考虑到速度变化的情况；文献[8]针对目标不机动时，防御弹与目标进行非合作博弈，基于A-CLOS设计制导律；文献[9]针对无人机和无人车的追逃微分对策问题，考虑了对局中障碍物的影响，确定了其分界界栅。

文献[10]针对控制能量作为制导性能指标，设计了飞机-导弹的双方追逃模型，并采用梯度迭代法求解;文献[11]针对视线倾角和视线偏角作为控制量，推导出了关于防御-拦截双方的末制导律;文献[12]针对三维空间三体追逃博弈问题，采用模糊评估的方法设计了目标函数并推导出了相应的控制策略;文献[13-16]针对多弹协同拦截单一目标进行制导律的设计，但是模型假设条件过于理想化，很难与实际情况相匹配;文献[17]针对拦截弹、防卫弹和攻击弹的三体博弈问题，分析了拦截弹赢得博弈的不同情况;文献[18]针对传统最优制导律的不足设计了最优边界制导律(OSBGL)，使得攻击弹可以逃脱防御弹并攻击飞行器;文献[19]针对高阶线性化拦截弹制导系统，研究了目标最优机动突防策略问题。

以上关于微分对策制导的研究大多数只关注末制导阶段，但是末制导阶段由于存在飞行器速度过快、对抗时间短等问题，难以体现出微分对策制导的优势。

本文针对攻击弹如何有效打击地面目标的问题，建立了三体攻防博弈模型，提出了一种基于微分对策的制导策略，并且,该制导律在中制导阶段就可以体现出其优势，在防御弹以三点法制导拦截的前提下，对比分析了攻击弹分别以比例导引和微分对策制导的仿真结果，验证了微分对策制导相比于传统制导策略的有效性。

1 问题描述与建模

本文考虑的是攻击弹A如何有效打击地面目标T，并且可以躲避以三点法制导的防御弹D三者间的攻防博弈问题。3个参与者在三维空间内的地面坐标系中的几何交战关系如图 1所示，假设地球为平面且y轴垂直向上为正，目标为静止状态。

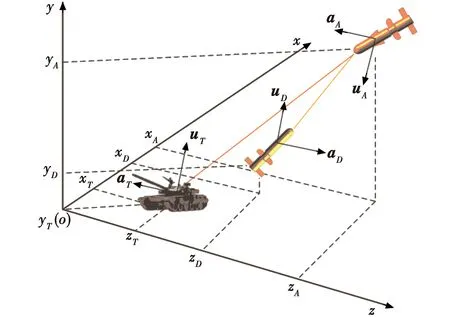
图1 交战三体几何关系Fig.1 Three-body engagement geometry

将地面目标、防御弹和攻击弹在地面坐标系中的坐标分别设为(xT,yT,zT),(xD,yD,zD)和(xA,yA,zA)。速度矢量分别设为uT=[uxT，uyT，uzT],uD=[uxD，uyD，uzD]和uA=[uxA，uyA，uzA]；加速度矢量分别设为aT=[axT，ayT，azT],aD=[axD，ayD，azD],aA=[axA,ayA,azA]；飞行器间的相对位置矢量为ri j=[xi j，yi j，zi j]；相对速度矢量为ui j=[uxij，uyij，uzij]；相对加速度矢量为ai j=[axij，ayij，azij]。

根据图1中定义的运动学变量，交战三体在地面坐标系下的相对运动学方程可为

(1)

设状态变量X=[ri j，ui j]T，因为目标为静止状态，所以状态方程仅表示攻击弹与防御弹之间的关系，则式(1)可写为

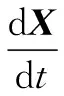
(2)

2 制导回路设计

在构建微分对策制导回路的问题时，分别采取了如下假设。

1) 系统获取飞行器状态是准确的，即不考虑系统状态估计误差的情况。

2) 自动驾驶仪为一阶滞后环节[20]，即

(3)

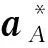
针对上述问题及假设条件设计如图2所示的制导框图。

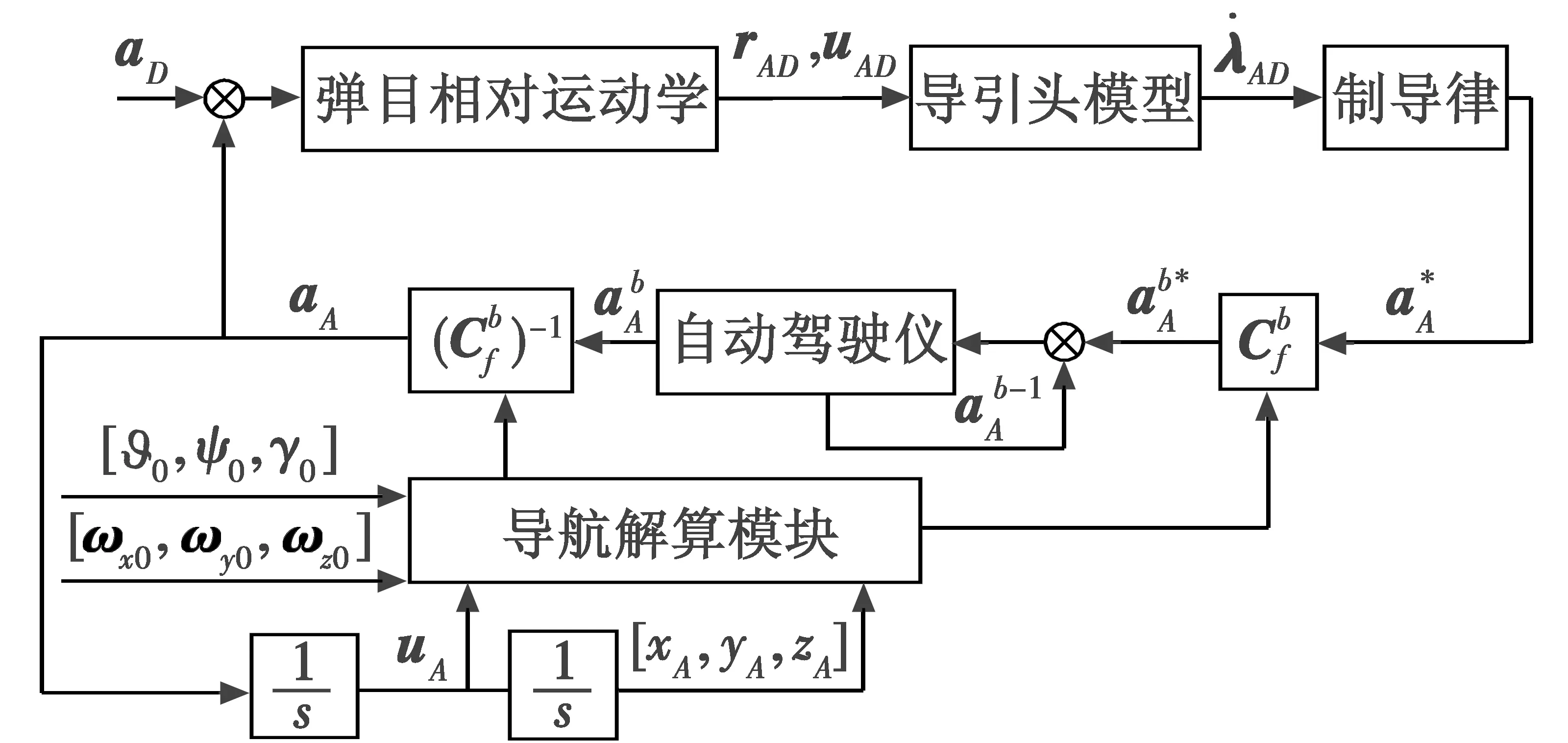
图2 制导框图Fig.2 Block diagram of the guidance

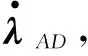
3 微分对策制导律的设计

在防御弹与攻击弹的攻防对抗中，防御弹总是力图使其与攻击弹的脱靶量达到最小值，而攻击弹则力图使其与防御弹的脱靶量达到最大，所以两者的攻防问题是一种零和博弈问题，而对于攻击弹和目标的零和博弈问题，由于目标静止两者间的问题就变成了攻击弹单方的追击问题，综合这两种情况可以得出防御弹以及攻击弹的制导策略。本文选择以最终的脱靶量和飞行器的需求过载作为综合性能指标，设计了如下目标函数

(4)

式中：t,t0,tend分别为当前时刻、初始时刻和终止时刻；N∈R4×4,为半正定的终端性能加权矩阵;Q∈R4×4,为半正定的当前状态性能加权矩阵;RD∈R6×6,RA∈R6×6，均为飞行器控制性能正定矩阵。

(5)

式中，λ∈R6×1,为协态变量。

根据微分对策问题解得最优解的必要条件并结合式(5)可得[21]

(6)

式中：X0,X(t0),X(tf)分别为状态变量初值、起始时刻与终止时刻值;λ(tf)为协态变量终值。

对哈密顿函数求导使其等于零，可以得出三体追逃博弈中防御弹和攻击弹各自的制导律如下

(7)

假定协态方程为

λ=PX

(8)

式中,P∈R6×6,是黎卡提微分方程的解。结合式(7)、式(8)可得

(9)

将式(6)代入式(2)可得黎卡提微分方程为

(10)

通过对黎卡提微分方程求解即可得到加速度控制指令的数值解，这里不对求解过程进行具体推导。本文为了体现微分对策制导的特点做了如下简化：

1) 在攻防对抗的过程中，重点只关注制导终端时的状态，所以可令当前状态性能指标矩阵Q=0；

2) 由于终端性能指标只表示终端时刻tend的性能，所以令终端性能指标矩阵N为常数矩阵。

4 仿真试验及分析

仿真中需要的初始数据如表1所示，试验中地面目标保持静止状态。

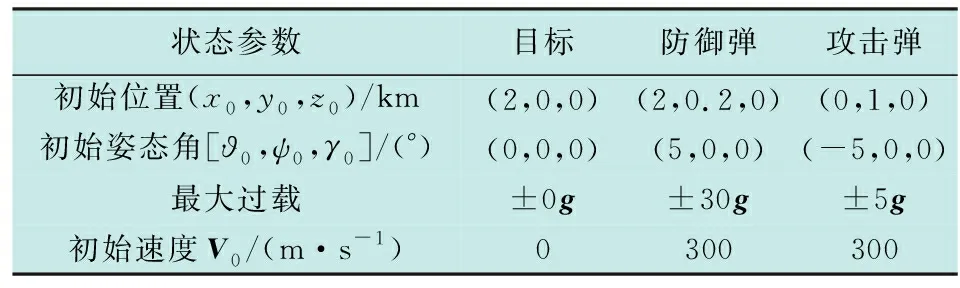
表1 初始仿真参数Table 1 Initial simulation parameters

由于导弹在实际飞行的过程中，弹体上的各种仪器所能承受的载荷有限，以及弹体本身的气动布局，操纵机构所能产生的舵偏角有限等因素，弹体上的过载往往达不到理想的设定值，因而对攻击弹的过载进行约束。

为了说明本文设计的制导律的有效性，可使防御弹以一个较大的过载值飞行，目的是为了使防御弹有更强的机动性追踪攻击弹，以此来验证攻击弹是否能在躲避防御弹的同时对目标进行拦截，因此不对防御弹的过载进行约束。

防御弹采用三点法导引，加速度控制指令为

(11)

式中：ηy,ηz分别为导弹控制指令与法相、侧向控制力的关系;qA，qD分别为攻击弹与防御弹的视线角;εA，εD分别为攻击弹与防御弹的方位角。

4.1 比例导引

当攻击弹采用比例导引时，加速度控制指令为

(12)

(13)

式中：ωAD为防御弹与攻击弹之间的相对视线旋转角速率矢量;K=diag(0，Ky，Kz),Ky,Kz为导航比。

图3所示为攻击弹在采取比例导引的运动轨迹。

图3 xoz和xoy平面运动轨迹(比例导引)Fig.3 The trajectory in xoz and xoy plane(proportional guidance)

从图3中可看出,防御弹和攻击弹在偏航方向上的轨迹变化不大，而从纵向平面的变化曲线可以看出,防御弹与攻击弹的距离过近。

比例导引情况下的过载变化曲线如图4所示。

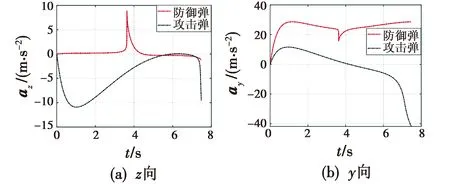
图4 z向和y向的过载变化曲线(比例导引)Fig.4 Acceleration variation in z and y direction(proportional guidance)

仿真结果表明,在攻击弹采用比例导引时，由于不涉及逃避防御弹的策略，攻击弹和防御弹的过载值都较为平稳。

攻击弹采取比例导引时，其三维空间示意图见图5。

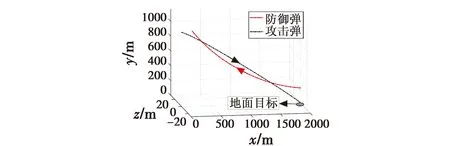
图5 比例导引的三维示意图Fig.5 Three-dimensional schematic diagram of proportional guidance

4.2 微分对策制导

当攻击弹采用如式(6)所示的加速度控制指令时，其运动轨迹如图6所示。

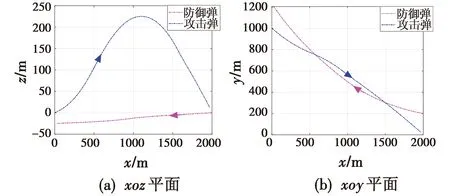
图6 xoz和xoy平面运动轨迹(微分对策制导)Fig.6 The trajectory in xoz and xoy plane(differential game guidance)

仿真结果表明,xoz平面的轨迹变化较小，xoy平面轨迹变化与比例导引时有明显差异。

微分对策导引情况下的过载变化如图7所示。

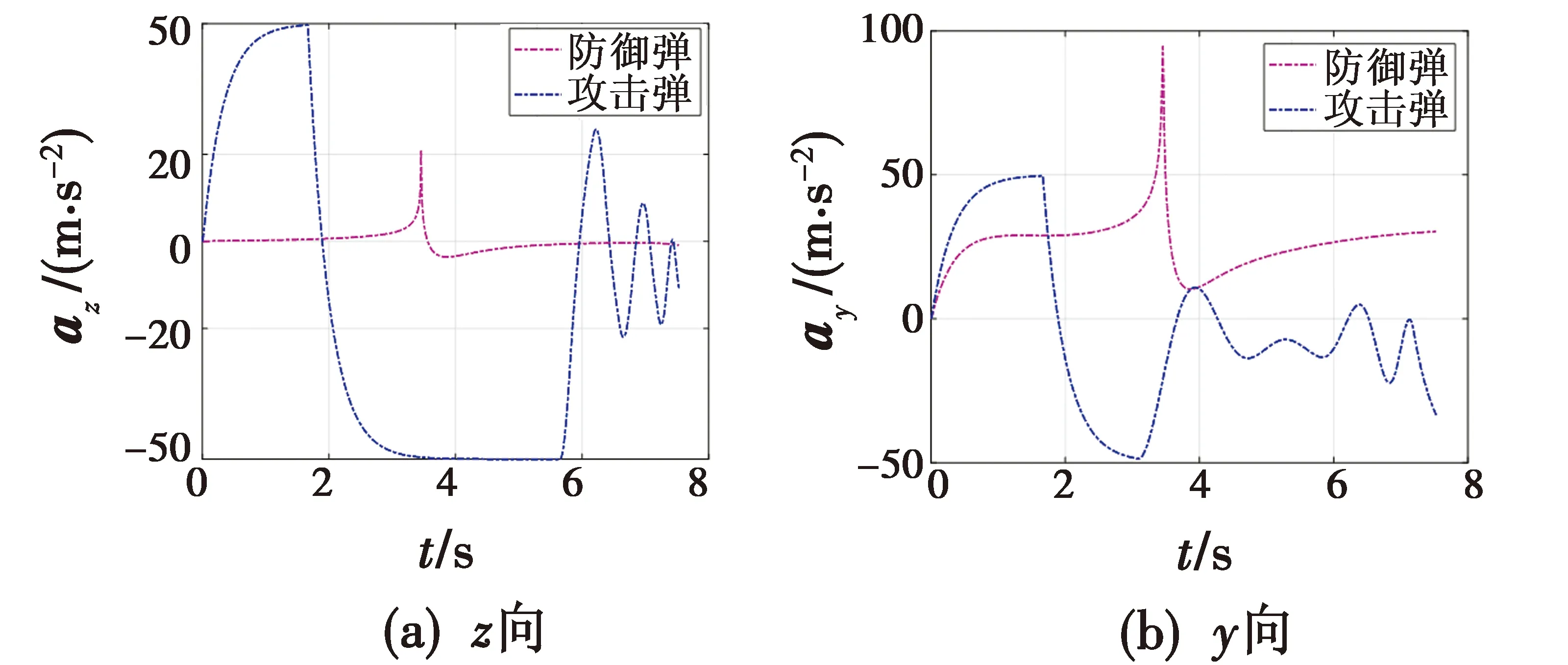
图7 z向和y向的过载变化曲线(微分对策制导)Fig.7 Acceleration variation in z and y direction(differential game guidance)

仿真结果表明，攻击弹为了躲避防御弹的拦截,过载值会有较大的变化，而防御弹为了拦截攻击弹,自身的过载也增大，这体现了微分对策制导的优势，既延长两者相对距离，又增大了防御弹的能量消耗。

图8为攻击弹采用微分对策制导时的三维空间示意图。

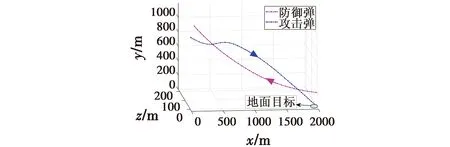
图8 微分对策三维空间示意图Fig.8 Three-dimensional schematic diagram of differential game

4.3 仿真结果分析

当攻击弹分别采用比例导引和微分对策制导时，防御弹与攻击弹的最小弹目距离，以及攻击弹的最终脱靶量如表2所示。

表2 弹目距离与脱靶量仿真结果Table 2 Simulation results of missile-target distance and miss distance m

由表2中的仿真数据可以看出:若攻击弹采取比例导引制导时，虽可打击目标,但攻击弹与防御弹之间的最小弹目距离较小，导致了在攻击弹打击目标之前就可能被防御弹拦截;而当攻击弹采取微分对策制导时,不仅可以减少与目标间脱靶量，并且延长了攻击弹和防御弹之间的最小弹目距离，使得攻击弹能在逃脱防御弹的同时对目标进行打击，展现了微分对策制导的优势。

5 结束语

本文针对攻击弹如何有效打击地面目标的问题，提出了一种在三方对抗博弈场景下的微分对策制导律，并且将其作为攻击弹的制导方式，考虑了交战参与者的理想情况及实际运动情况，对参战三方的运动轨迹和过载变化进行了数值仿真，由仿真结果可得出,攻击弹采取微分对策制导时与传统的比例导引制导方法对比有明显的优势，因此仿真结果具有一定的有效性和实际性。