基于非线性回归的杂波重构STAP方法

邹 帛， 王 欣， 冯为可， 朱晗归， 李 瑶

(空军工程大学防空反导学院，西安 710000)

0 引言

机载相控阵脉冲多普勒雷达所接收到的回波信号包含目标的角度和多普勒信息，为了实现杂波背景下的运动目标检测，空时自适应处理(Space-Time Adaptive Processing，STAP)通过采集相邻距离单元的回波信号样本，估计杂波加噪声协方差矩阵(Clutter plus Noise Covariance Matrix,CNCM)，并联合目标的空时信息，自适应地设计滤波器权矢量，进而在角度和多普勒域抑制杂波，实现杂波背景下的动目标检测[1]。文献[2]表明，若使得输出信杂噪比的损失不超过3 dB，则至少需要2倍雷达系统空时自由度(Degree of Freedom,DoF)的独立同分布(Independent and Identically Distributed,IID)距离单元样本[2]。

当机载雷达处于正侧视观测模式且杂波环境较为平稳时，雷达可以轻易地获得足够的样本实现STAP。然而实际中，机载雷达的应用场景多变且杂波环境的变化可能较为剧烈，自适应处理的难度体现在难以获得足够的IID距离单元样本[3-5]。为了提高复杂杂波背景下的动目标检测性能，出现了一些针对性的方法，包括实现样本筛选的功率选择训练(Power Selected Training,PST)方法[6]、非均匀检测器(Non-Homogeneity Detection,NHD)方法[7]，仅利用待测距离单元(Range cell Under Test,RUT)信号的直接数据域(Direct Data Domain,DDD)方法[8]和利用了地形信息的知识辅助(Knowledge-Aided,KA)[9]方法等。近年来，压缩感知(Compressed Sensing,CS)理论和稀疏恢复(Sparse Recovery,SR)技术得到了快速发展[10-11]，并被应用于空时自适应处理领域，SR-STAP方法逐渐展现出了小样本条件下杂波抑制的巨大潜力，在IID距离单元样本严重不足条件下，可以实现杂波谱的高分辨估计，有效地提升了机载雷达杂波背景下的动目标检测性能[12-14]。

SR-STAP方法突出的优点在于实现同样的杂波抑制性能需要的IID距离单元样本更少，但同时也面临着求解精度有待提高的问题。SR-STAP方法将空时平面离散成网格时存在一定的量化误差，引起了字典失配的问题[15-16]，同时，其在杂波谱的求解过程中也面临着SR算法参数设置困难的问题，不合适的参数设置会导致迭代结果不收敛，杂波脊以外的空时平面会出现离散的功率值[17-18]，即使SR算法得到了合适的参数预设置，在不同的杂波环境下，迭代的收敛性也不一定能得到保证。当存在未知偏航角时，杂波的稀疏性下降，网格失配效应加剧，且非平稳的杂波特征提高了SR算法参数设置的难度[19-20]，这些问题都进一步降低了SR算法的求解精度和SR-STAP方法的杂波抑制性能。

针对上述问题，本文在分析杂波非平稳特性的基础上，提出了一种基于非线性回归的杂波重构方法。该方法对杂波脊参数和杂波谱的权值进行特定的非线性回归处理，滤除了由杂波稀疏性降低引起的脊外干扰，精确地估计出杂波脊模型的参数和杂波功率的分布。仿真结果表明，该方法能够有效提高杂波抑制和动目标检测的性能。

1 基础知识

1.1 信号模型

图1所示为机载雷达的几何模型。图1中，均匀线阵(Uniform Linear Array,ULA)机载雷达正侧视平飞，阵元数为M，阵元间距为d，在一个相干处理间隔(Coherent Processing Interval,CPI)内脉冲数为N，脉冲重复间隔为Tr，载机以速度v沿着Y轴正方向匀速飞行。

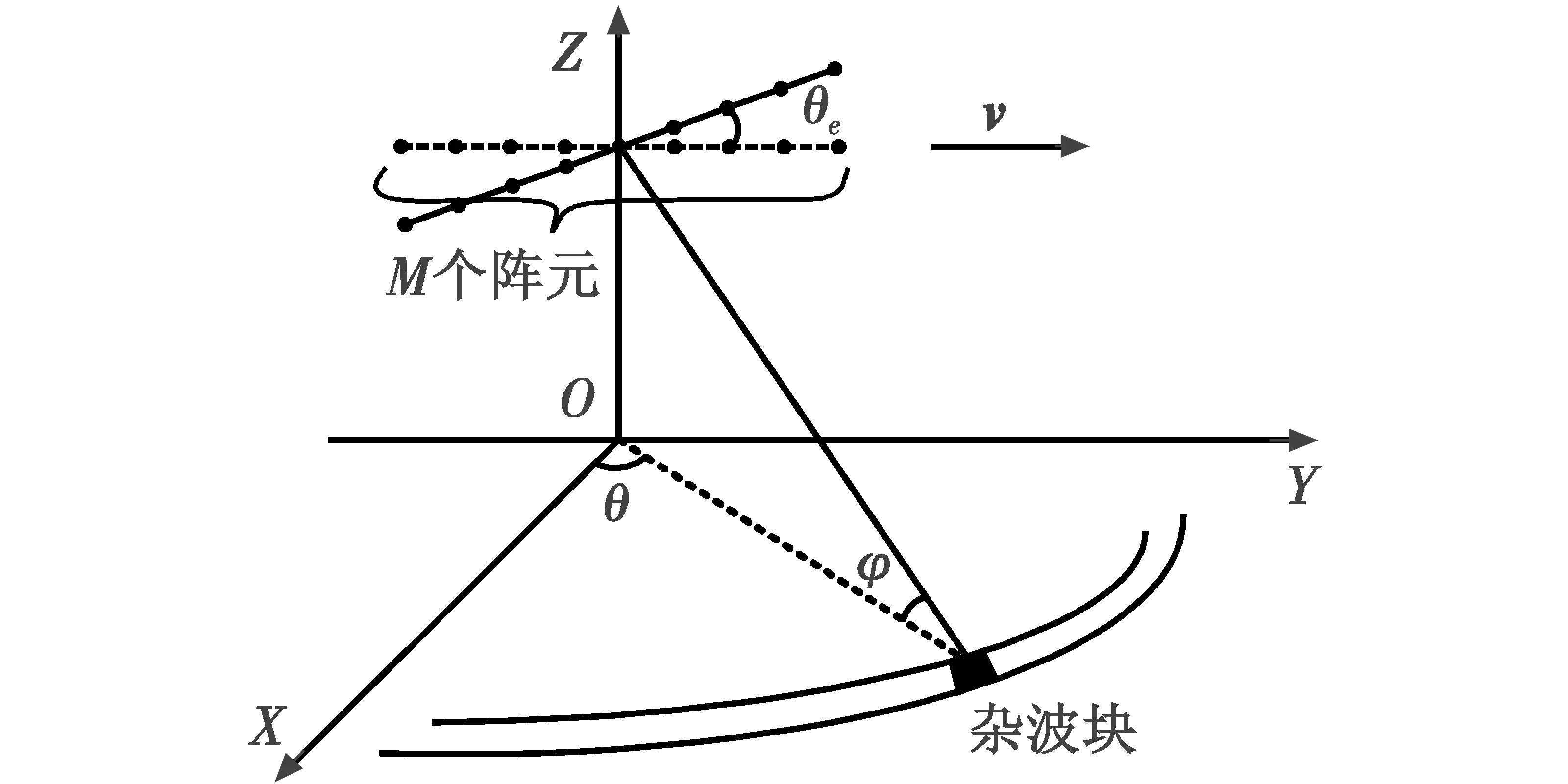
图1 机载雷达的几何模型Fig.1 Geometric model of airborne radar

不考虑距离模糊的影响，某一距离单元由Nc个相互独立的杂波块构成，接收信号x表示为

(1)

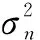
(2)

式中：φn和θn分别为第n个杂波块的俯仰角和方位角;θe为未知的偏航角；λ为信号波长。不考虑雷达背瓣接收到的信号，即观测角度仅为-90°～90°，有fc;s∈[-0.5cosφ,0.5cosφ]，杂波块的空域频率和多普勒频率的关系为

(3)

根据式(1)，假设杂波和噪声相互独立，以Rc，RN和INM分别表示杂波和噪声的协方差矩阵以及维度为NM×NM的单位矩阵，CNCM可以表示为

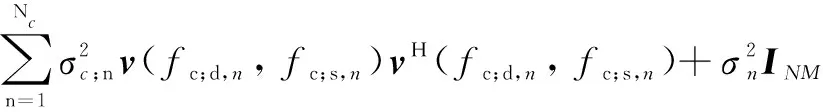
(4)

在空时滤波器权矢量为w时，STAP输出数据为y=wHx。为使得输出信号的信杂比最大，空时滤波器权矢量表示为

(5)

传统样本矩阵求逆(Sample Matrix Inversion,SMI)方法估计杂波特性的过程表示为

(6)

式中，L为距离单元样本数目。由RMB准则可得SMI-STAP方法和最优STAP方法的输出SINR之比为

(7)

式中,K=MN,为系统自由度。若L≥2K，则SMI方法的RSINR,loss≤3 dB。

1.2 SR-STAP

杂波信号可以由Nc个杂波块对应的空时信号叠加而成，因此，可将整个空时平面离散化为Ns=ρsM和Nd=ρdN个网格点(ρs和ρd分别为空域频率和多普勒频率的离散化因子,且通常有NsNd>>NM)，其中分别表示分尺度则空时回波信号中所包含的杂波分量为

(8)

式中：Φ表示NM×NsNd维的完备的空时导向矢量字典，具体表示为

Φ=[v(fd,1,fs,1),v(fd,1,fs,2),…,v(fd,Nd,fs,Ns)];

(9)

角度-多普勒像γ=[γ1,1,γ1,2,…,γNd,Ns]代表杂波在空时字典Φ上的强度，则距离单元样本的信号为

x=xc+n=Φγ+n。

(10)

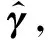
(11)

s.t.||xl-Φγ||2≤η

式中：||·||1表示L1范数;η表示观测噪声水平。

(12)

根据获得的CNCM估计结果，空时滤波器的最优权矢量为

(13)

2 基于非线性回归的杂波重构STAP方法

SR-STAP方法虽然能够应用于训练距离单元样本严重缺失的极端情况，但同时也面临着空时字典失配、参数设置困难等问题，尤其在存在未知的偏航角时，杂波的稀疏度降低且呈现非平稳特性，这些问题都进一步降低了SR-STAP方法的杂波抑制性能。

存在θe=30°的偏航角时杂波谱的理论值如图2(a)所示，基于SR算法获得杂波谱的估计值如图2(b)所示。

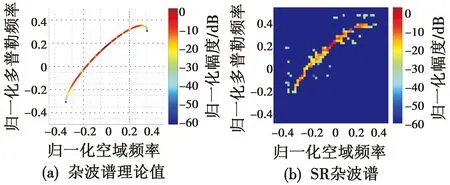
图2 杂波谱的理论值和估计值Fig.2 Theoretical and estimated value of clutter spectrum

对比分析可知：SR杂波谱的杂波脊特征得到了一定程度的恢复，但是杂波脊以外的空时平面存在离群的杂波功率散点，其回归于主杂波脊；SR杂波谱在空时平面上的权值分布也存在一定规律，即杂波脊位置上的权值显著较大。为了解决上述问题，本文提出了一种基于非线性回归的杂波重构方法。

首先，存在偏航角的杂波脊模型已经给出，由于先验条件不一定完全准确，所以可以根据SR的结果对杂波脊的模型参数进行精确的估计。考虑到杂波谱及其对应权值在空时平面上的分布情况，可以对杂波谱在空时平面上进行坐标加权的非线性回归，坐标加权的目的在于利用权值的分布倾向使估计结果更加逼近真实的杂波脊。

提取杂波谱非零点的坐标(fc;s,i,fc;d,i)和权值γi作为一组数据ei(i=1,…,I，I为数据组ei的个数)。同时,将杂波脊模型表示为参数θe和空域频率fc;s的函数

fc;d=fc;d(θe,fc;s)

(14)

对于杂波脊模型参数θe的加权估计可以表示为

(15)

(16)

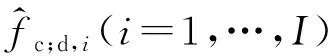
(17)

以此利用3σ准则进行离群值的剔除，多次迭代上述的坐标加权非线性回归和离群值剔除步骤，得到杂波脊模型参数的精确估计，并保留迭代筛选后留下的数据组{ei|i∈Ωi}。迭代次数取决于设置的离群度ε，当迭代结果的RMSE(用ERMSE表示)小于ε，可认为筛选后的数据足够集中，停止迭代。

然后,考虑到雷达波束的方位加权效应，需要对杂波谱在方位上进行非线性回归。归一化波束形成器的响应解析式为

(18)

式中，θ0为波束扫描角度。联立fc;s(θ,φ)，响应的解析式可以写成

(19)

将杂波谱在空域维表示成空域频率和杂波强度的函数，可得

γs(fc;s,σmax)=σmaxy(fc;s)

(20)

式中,σmax为波束主瓣方向上杂波块的回波强度，对于σmax的估计可以表示为

(21)

式中,Ωi表示所有迭代筛选后的杂波谱分量的集合。所以经过非线性回归得到杂波谱的估计

(22)

至此，已经完成了杂波脊模型参数和杂波谱功率的精确估计，为了还原真实的杂波信号，将杂波块按照角频率分辨率划分，杂波信号表示为

(23)

式中，Nc为杂波块划分个数，同时，经过杂波重构后的干扰协方差矩阵即为

(24)

综合以上的两个非线性回归环节，杂波重构的流程如图3所示。

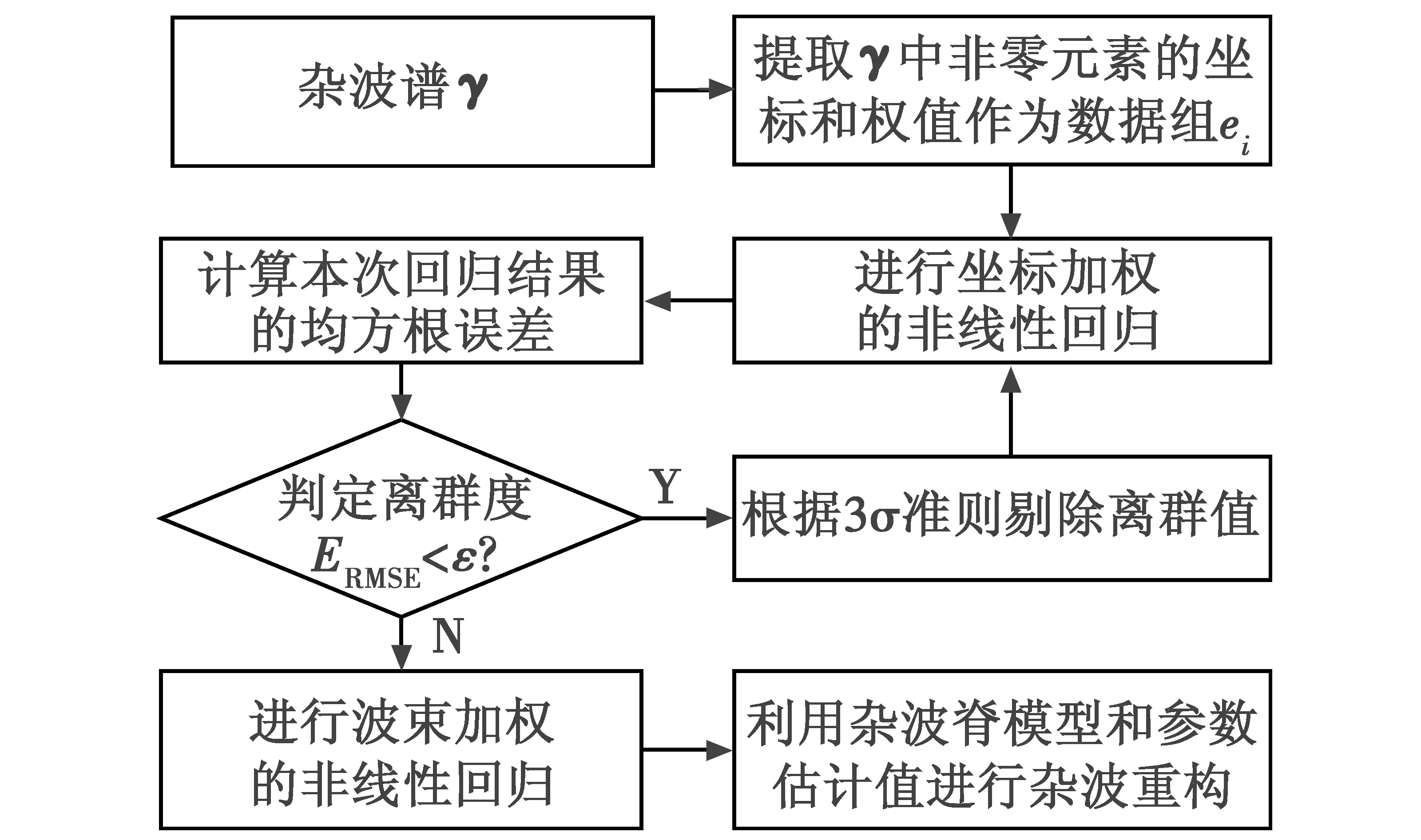
图3 杂波重构流程图Fig.3 Flow chart of clutter reconstruction

3 仿真分析

3.1 可行性分析

不同迭代次数下的筛选结果如图4所示。

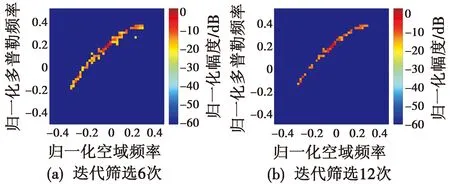
图4 不同迭代次数下的筛选结果Fig.4 Screening results after different iterations

对图2(a)中提取出来的数据组ei进行坐标加权的非线性回归，迭代次数为6和12时的数据筛选结果分别如图4(a)和图4(b)所示，可以看出，随着迭代次数的增加，脊外散点逐渐减少，杂波谱收敛于一条清晰明确的杂波脊。

离群度ε≤10-2，对迭代筛选剩下的数据组进行杂波谱的非线性回归处理，处理示意图及结果见图5。

图5 杂波谱的非线性回归处理Fig.5 Nonlinear regression processing of clutter spectrums

由图5可以看出,对于杂波散点进行拟合，方向图主瓣上的杂波强度略高于300，与仿真条件中天线主瓣方向上杂波功率较为吻合。

基于非线性回归的结果，得到重构杂波的MVDR功率谱如图6(a)所示，图6(b)为SR-STAP方法获得的杂波MVDR功率谱图，对比表明了本文重构方法对还原杂波信号的有效性和可行性。

图6 杂波重构后的空时功率谱Fig.6 Space-time power spectrum of reconstructed clutter

3.2 迭代速度和估计精度分析

以上的筛选结果对比仅体现了迭代次数的作用效果，本质上,离群度ε的设置直接决定了迭代筛选的次数和参数估计的精度。选取合适的离群度范围，进行多组非线性回归和数据筛选处理，可以得到如图7所示的曲线，其描述了离群程度对非线性回归估计的参数误差和迭代次数的影响。

图7 离群度ε对非线性回归的影响Fig.7 Effect of outlier degree ε on nonlinear regression

仿真结果表明,随着离群度ε的降低，即要求数据组在空时平面上的分布更加集中，迭代次数的增加速度加快，尤其在离群度ε小于0.05之后，所需的迭代次数骤加。随着迭代次数的增加，参数误差迅速收敛至10-2左右并趋于平稳，此时所需的迭代次数仍接近10。对比2组数据，可以选择合适的离群度ε设置值，在保证参数估计精度较高的同时，尽可能减少迭代次数。

3.3 杂波抑制性能分析

杂波重构方法的性能主要由杂波脊参数和杂波功率2项估计值的准确程度决定。在本文仿真实验中，随着离群度ε设置值的减小，杂波脊参数逐渐收敛于真实的偏航角。对ε=10-2时的迭代结果进行分析，杂波重构得到RI的特征索引如图8所示，其中，DOF表示空时自由度。

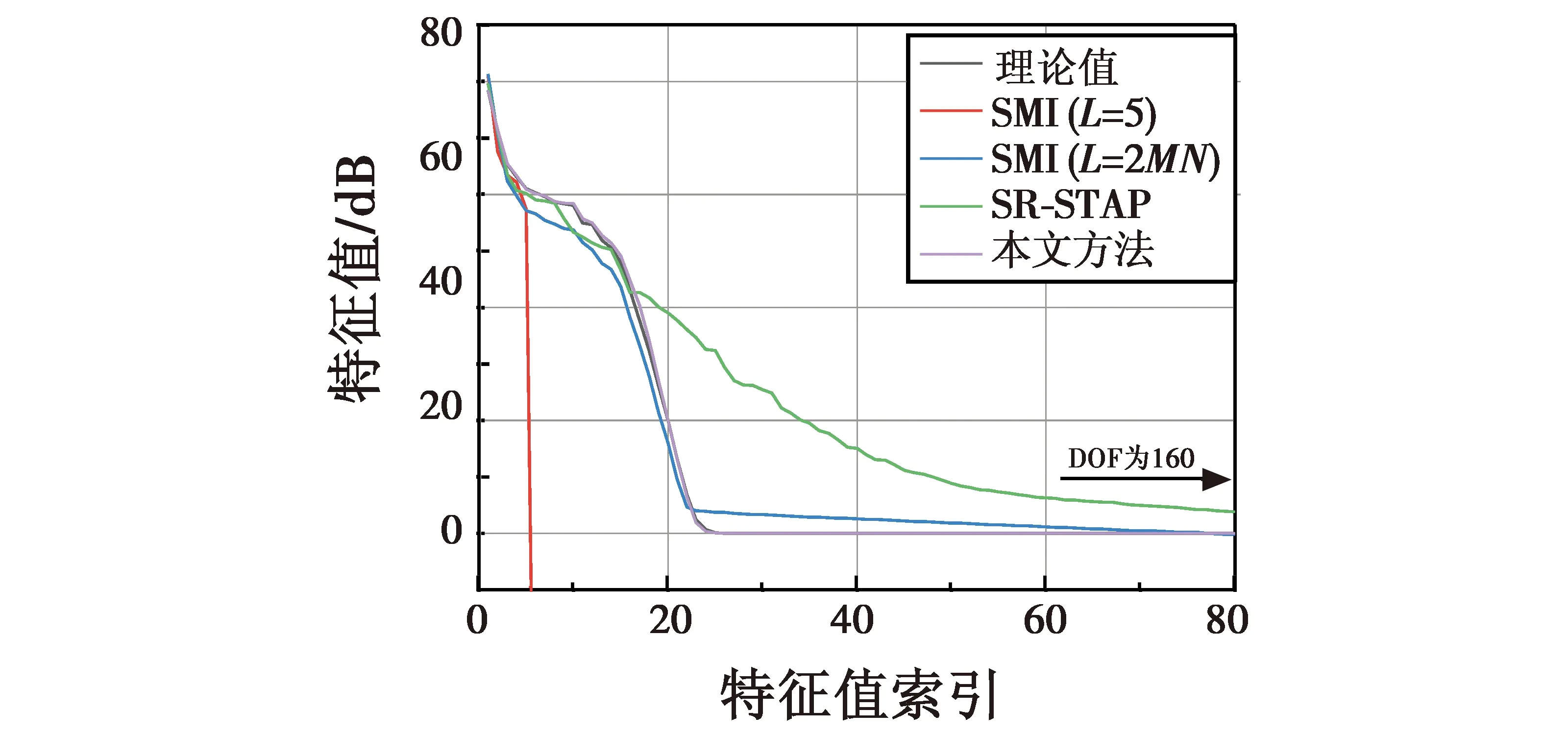
图8 不同RI的特征值索引Fig.8 Eigenvalue index of different RI

对比各方法的特征值索引，采用5个样本的SMI方法使得干扰信号中杂波分量的有效秩损失严重，同时，基础稀疏恢复方法使得杂波的有效秩严重扩展。根据RMB准则，2MN个样本的SMI方法使得杂波分量的有效秩接近精确值，而杂波重构方法的结果和精确值近乎重合。本组对比证明了本文杂波重构方法对于杂波的恢复具有优秀的性能。

在得到干扰协方差矩阵的基础上，分别对比Opt-STAP方法、L=160的SMI-STAP方法、SR-STAP方法和本文方法得到的空时滤波器权矢量的空时响应，如图9所示。

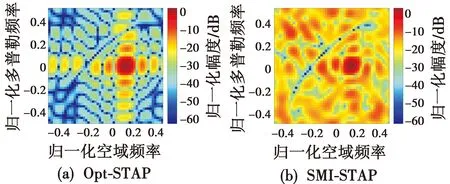
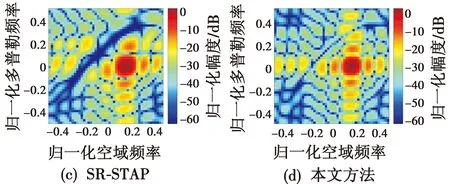
图9 各STAP方法形成权矢量的空时响应Fig.9 Space-time response of the weight vector from each STAP method

由图9可知，本文方法的空时响应最接近最优权矢量的响应，通过图9(b)-图9(c)的比较可知，本文的杂波重构方法对杂波脊的抑制效果明显优于基础的SR-STAP方法，并接近于最优权矢量的杂波抑制效果。

图10所示为对比各STAP方法在天线主瓣方向上的SINR损失。由图10可知，各STAP方法均在空时平面针对杂波信号形成功率凹陷，起到了抑制杂波、提高信杂比的效果，但凹口的宽度和深度会显著区别STAP的效果。对比分析可得，L=160的SMI方法可以达到比较好的杂波抑制效果，但同时各个速度的目标均有近15 dB的SINR损失，几乎完全损失了动目标检测能力。SR-STAP方法保证了一定的动目标检测能力，但凹口仍然较大，在一定的速度范围内造成目标丢失。与之相比，本文方法具有相同的杂波抑制效果，且对于不同速度的目标都有优秀的SINR损失，凹口宽度有明显改善，动目标检测性能更接近于最优权矢量。

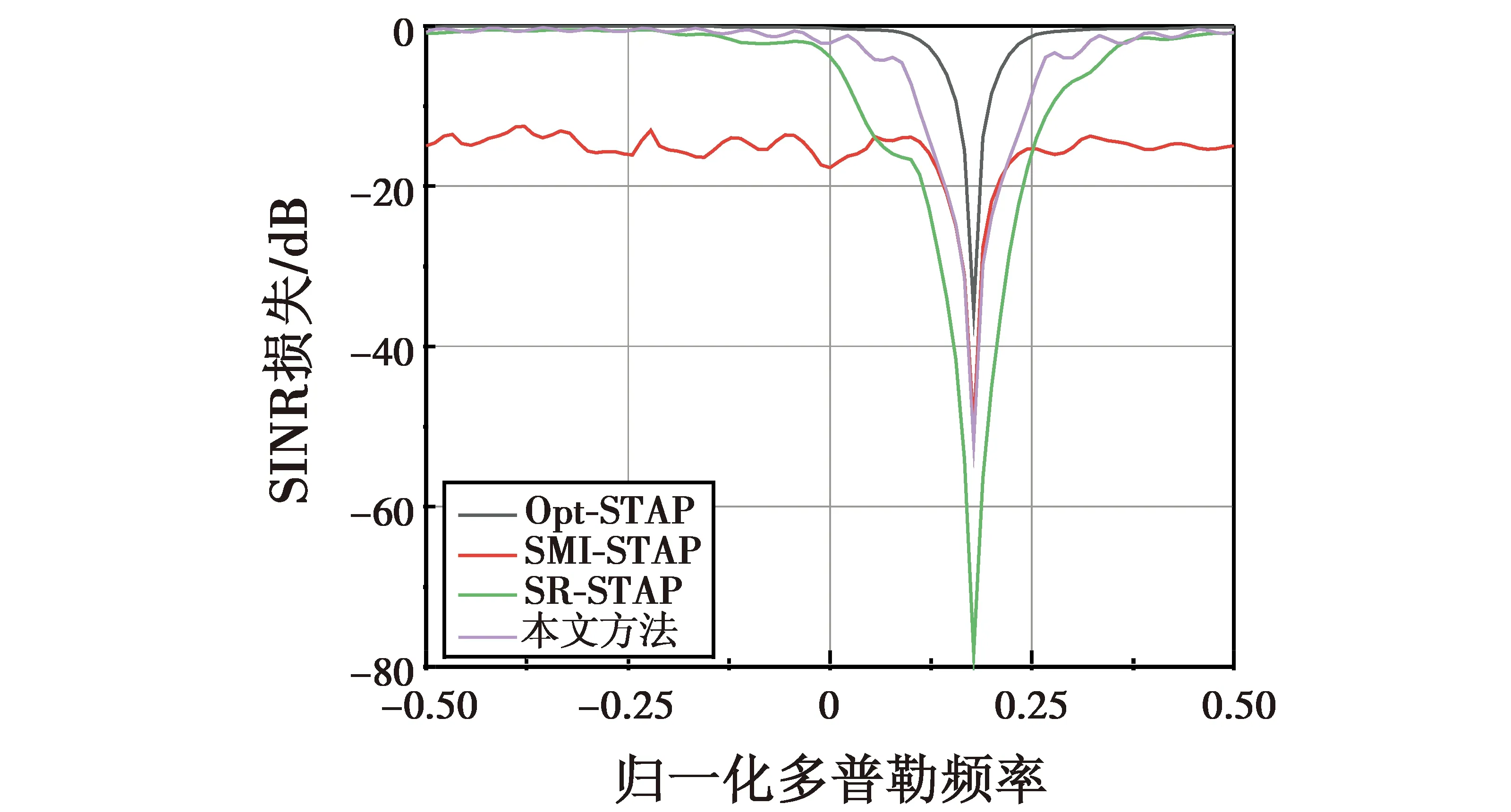
图10 各STAP方法性能对比Fig.10 Performance comparison of different STAP methods

4 结束语

当存在未知偏航角时，SR-STAP方法杂波抑制性能一般，且容易丢失动目标，性能明显有待提高。本文提出的基于非线性回归的杂波重构，优化了SR-STAP方法的处理结果，仿真实验表明，在存在未知偏航角的非平稳杂波环境下，该方法基于有限的杂波距离单元样本，有效地提高了机载雷达杂波抑制的性能，同时可以根据实际的场景，合理设置离群度的值，用以控制迭代次数和参数估计精度。