考虑逆向可变车道的预信号公交优先控制

王予瑞，刘昱岗,3，郑 帅

（1.西南交通大学，交通运输与物流学院，成都 611756；2.综合交通运输智能化国家地方联合工程实验室，成都 611756；3.四川省交通运输发展战略和规划科学研究院，成都 610041）

0 引言

为缓解城市交通拥堵，有学者提出公交优先策略，该方法现已广泛应用于城市道路及交叉口。公交信号优先控制是交叉口实施公交优先的重要方法之一，目的是使公交车辆快速通过交叉口，节约乘客出行时间，有效提高公共交通吸引力，进一步优化城市客运交通结构。

在预信号公交优先控制研究方面，季彦婕等[1]提出设置预信号可实现公交优先，有效减少公交延误，但会增加社会车辆延误。张卫华等[2]提出基于公交优先的预信号交叉口进口道双停车线间距计算方法。张斌华等[3]针对预信号公交优先控制策略中“先红先绿”控制方式造成的社会车辆二次停车问题，改善了信号协调配时方案。王涌龙等[4]以次路侧型公交专用道为研究对象，提出基于公交待行区的预信号控制方法。邓明君等[5]提出基于公交优先与综合待行区的交叉口交通组织设计及信号控制方法，讨论进口道布局形式和设置条件。陈永恒等[6]提出基于公交预信号的可变公交车道（Variable Bus Approach Lane，VBAL）控制方法，提出交叉口渠化设计方案和主预信号控制模型，建立了车辆延误变化计算模型。

在非常规交叉口设计方面，有学者提出逆向可变车道（Contraflow Left-turn Lane,CLL）设计方法，该方法通过在交叉口出口道靠近道路中线内侧设置逆向可变车道，通过信号配时赋予不同类型车辆通行权，进而提升交叉口通行能力。逆向可变车道已在我国邯郸、长沙、济南[7]等城市交叉口展开应用实践。赵靖等[8]基于传统交叉口信号配时优化方法对设置逆向可变车道的交叉口进行分析，结果表明其方法能提高左转车道通行能力。Wu 等[9]提出一种分析模型估计设置逆向可变车道的交叉口通行能力和车辆延误，结果表明其方法相较于串联交叉口[10]（TandemIntersection,TI）产生延误更少。Liu等[11]学者提出设置逆向可变车道交叉口间最小距离的计算方法。Wu 等[12]提出逆向可变车道设计的感应控制策略，通过优化主、预信号间距，提高交叉口通行能力并降低左转车辆延误。任其亮等[13]以周期时长、主预信号控制、逆向可变车道长度及饱和度等为约束，建立交叉口信号配时双目标优化模型，结果表明该方法更适合高流量交叉口。

在预信号公交优先控制和逆向可变车道设计方法结合应用方面，Guler[14]在上游设置预信号使公交利用对向车道通过交叉口，提出单进口道公交优先控制策略并探讨其适用性。Zhao[15]和安实[16]等均提出一种动态公交专用道设计方法，使位于出口道的左转公交专用道可在各相位内动态用于左转公交和其他车辆。Shu 等[17]提出具有公交车引导和优先控制模型的可变公交进口道设计方法，可以实现直行和左转公交优先。

笔者注意到现有文献对利用对向车道实现公交优先的研究较少，已有的研究也存在社会车辆延误增量较大、公交车辆在交叉口内部的行驶距离过长等问题，且多数方法仅能保证在同一方向上的公交车流优先。基于此，本文以单点信号控制交叉口为研究对象，提出一种考虑逆向可变车道的预信号公交优先控制方法，在保障公交优先的基础上，实现左转社会车辆与左转公交车辆同时通过交叉口，减小交叉口人均延误，进一步提高交叉口时空利用率和通行效率，并减少设置预信号给社会车辆带来的不利影响。算例分析验证了本方法的有效性和可行性。

1 交叉口几何布局与相位设计

1.1 交叉口几何布局

设置逆向可变车道的预信号交叉口进口道布局形式如图1 所示，在东西进口道上设置有1 条路侧型公交专用道、1 条直行专用道、1 条左转专用道、2条渠化右转车道以及1条逆向可变车道，逆向可变车道设置在靠近道路中线最内侧出口道上（图中阴影部分）。同时，预信号设置在直行与左转专用车道上游，在预信号停车线后设置有直行与左转社会车辆导向车道。

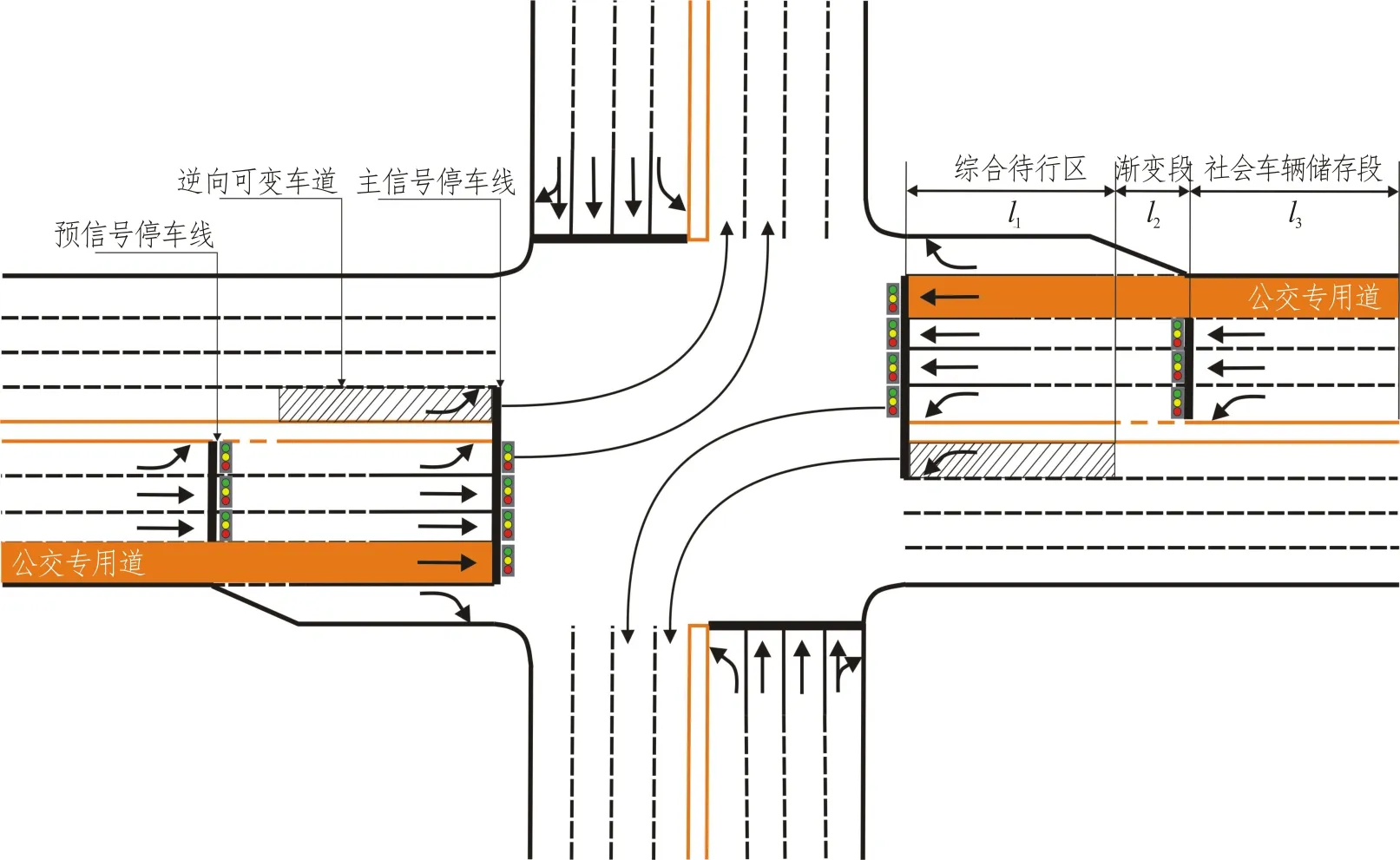
图1 设置逆向可变车道的预信号交叉口几何布局示意图Fig.1 Geometric layout of pre-signalized intersection based on contraflow left-turn lane

设置有逆向可变车道的进口道共由三个功能路段组成，第一段为车辆综合待行区（即l1），在本方案中也指逆向可变车道长度；第二段为借道左转车辆渐变段（即l2），指车辆变道驶入逆向可变车道所需的中间开口长度，可类比于车道展宽渐变段；第三段为社会车辆储存段（即l3）。

1.2 交叉口相位设计

1.2.1 交通组织

假设在预信号交叉口的东西进口设置逆向可变车道，本方案中交叉口采用“先左转、后直行”相位组织思路，如图2所示。

图2 一个信号周期内各方向车流通行规则Fig.2 Traffic flow sequence in each direction during a signal cycle

一周期内车辆通行分为以下四个阶段：

（1）阶段一：南北左转。东西方向公交车进入综合待行区排队等候，左转公交进入常规左转车道排队，直行公交在其他车道排队，该相位内逆向可变车道为南北方向左转车辆出口道。若左转公交无法进入待行区，则向右变道驶入渠化右转车道，此时右转车道作为备用左转车道。

（2）阶段二：南北直行。主信号绿灯开启后数秒，东西方向预信号绿灯开启，左转车辆驶入逆向可变车道和常规左转车道（在左转公交车后排队），直行车辆驶入正前方车道排队，该阶段逆向可变车道为东西左转车辆进口道。

（3）阶段三：东西左转。左转公交与社会车辆驶出交叉口，该相位内逆向可变车道仍为东西左转车辆进口道，预信号绿灯持续，为保证逆向可变车道上的左转车辆在有效绿灯时间内清空，须在主信号绿灯结束前数秒，使左转预信号绿灯变红。

（4）阶段四：东西直行。左转预信号绿灯变红后，直行预信号绿灯持续，直行车辆可驶入常规左转车道排队，在主信号绿灯开启后与直行公交相继驶出交叉口，预信号在周期结束前数秒变红，该阶段逆向可变车道为东西直行车辆出口道。同时，在该相位内到达交叉口的东西左转公交车辆需变道驶入渠化右转车道排队。

1.2.2 车道放行情况

根据上述交通组织方案，一个信号周期内东西方向各类型车道在主、预信号停车线之间的车辆放行情况不同，如图3所示。

图3 主、预信号停车线之间各类型车道车辆放行情况Fig.3 Vehicle release of various lanes between main signal and pre-signal parking lines

2 主预信号协调优化模型

2.1 优化目标

以交叉口人均延误最小为优化目标，建立如下优化目标函数：

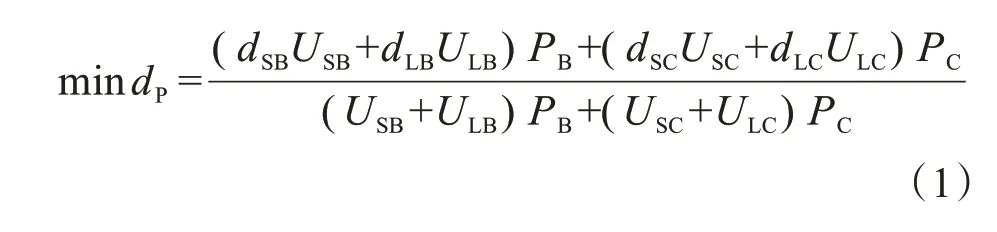
式中：dP为交叉口人均延误（s）；dSB,dLB分别为直行及左转公交车辆平均延误（s）；dSC,dLC分别为直行及左转社会车辆平均延误（s）；USB,ULB分别为高峰期直行、左转公交车辆到达率（pcu s），其中公交对社会车辆的当量转化系数为2.0；USC,ULC分别为高峰期直行、左转社会车辆到达率（pcu s）；pB,pC分别为公交车辆、社会车辆平均载客人数（per/pcu）。

2.2 基本假设

（1）公交与社会车辆均匀到达与离开，车辆在绿灯时间内的饱和流率固定；

（2）每一车道饱和流率相等；

（3）直行、左转预信号绿灯同时开启，主信号绿灯结束前，综合待行区内车辆消散完毕；

（4）直行与左转公交均利用公交专用道驶入综合待行区，且遵从“先远后近”停靠原则，待行区中所有车道均会被公交利用；

（5）本方法中右转车辆不受主、预信号控制，且车流量较小，不考虑其延误。

2.3 车辆延误计算

本节以累计到达-离去曲线法为基础，假设车辆到达服从均匀分布，根据交通组织方案，建立交叉口车辆延误计算模型。

2.3.1 直行车辆延误

本方案中直行车辆延误为车辆在主信号和预信号处产生延误之和。因公交车辆不受预信号控制，仅在主信号处产生延误，故分析主信号处直行车辆到达与离去过程可得到直行公交延误。

绘制本方案中直行车辆在主信号处的累计到达-离去曲线，如图4所示，阴影部分为一个信号周期内主信号处产生的直行车辆延误。

（1）直行公交车辆延误

图4 中折线OABCD表示直行车辆到达过程，线段OA表示预信号红灯期间，只有直行公交驶入综合待行区的到达曲线；线段AC表示直行预信号绿灯启亮后，社会车辆驶入综合待行区与直行公交驶入公交专用道时的到达曲线，直行车辆到达率增加，为直行公交和社会车辆到达率之和，直至预信号绿灯结束。线段CD表示预信号红灯启亮，社会车辆在预信号处排队等待，仅直行公交驶入综合待行区的到达曲线。

图4 主信号处直行车辆累计到达-离去曲线Fig.4 Accumulated arrival and departure curve of through vehicles at main signal

图4 中折线FBCD表示直行车辆离去过程，线段FB表示主信号绿灯启亮，直行车辆以饱和流率离开交叉口的离开过程曲线；线段BC表示主信号停车线后排队车辆消散后，车辆离开流率等于到达流率的过程曲线；线段CD表示预信号红灯启亮后，仅直行公交车辆驶出主信号停车线。

经分析得到图4 中四边形OAEF面积和三角形ABE部分面积之和即为一个信号周期内直行公交延误：式中：gL为左转车道预信号绿灯时间（s）；rP为直行车道预信号红灯时间（s）；t1为直行预信号绿灯相对主信号提前结束时间（s）；t3为左转预信号绿灯相对主信号提前结束时间（s）；NS为主信号处可用于直行的车道数；S为单车道饱和流率（pcu/s）。

四边形OAEF和三角形ABE面积按照式（4）、式（5）计算：

式中：C为一个信号周期时长（s）。

（2）直行社会车辆延误

本方案中社会车辆在主、预信号处均会产生延误，绘制预信号处直行车辆累计到达-离去曲线，如图5 所示，阴影部分为预信号处直行车辆延误。本节不再赘述预信号处车辆到达与离去过程，经分析得到图4 中三角形ABE部分面积、图5中四边形OGB'C'和三角形D'E'F'面积之和即为一个信号周期内直行社会车辆总延误。由相似三角形知识得四边形OGB'C'和三角形D'E'F'面积之和等于三角形A'B'C'的面积：

图5 预信号处直行车辆累计到达-离去曲线Fig.5 Accumulative arrival and departure curve of through private vehicles at pre-signal

2.3.2 左转车辆延误

本方案中对左转社会车辆设置有预信号，故左转车辆在主、预信号处均会产生延误，左转公交车辆仅在主信号处产生延误。

（1）左转公交车辆延误

主信号处左转车辆累计到达-离去曲线如图6所示，阴影部分为主信号处左转车辆总延误。图中折线ABFCMD表示主信号处左转车辆到达过程曲线，折线HFCME表示主信号处左转车辆离开过程曲线，本节不再赘述具体过程。经分析得到四边形OABPH、三角形BFP部分面积与三角形MDE面积之和为一个信号周期内左转公交车辆延误。由相似三角形知识得四边形OABG与三角形MDE面积之和等于三角形BGM'面积。

图6 主信号处左转车辆累计到达-离去曲线Fig.6 Cumulative arrival and departure curve of left turn vehicles at main signal

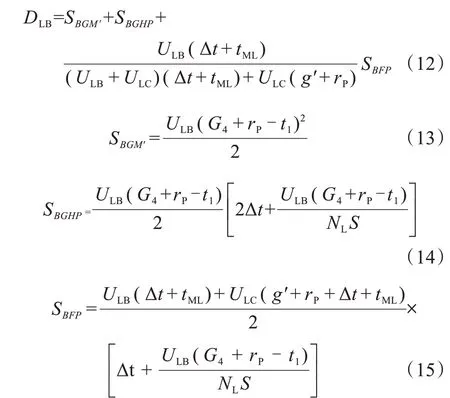
式中：G4为第四相位绿灯时间（s）；g'为直行与左转预信号绿灯时间之差（s）；Δt为预信号绿灯开启时间与第三相位绿灯开启时间差（s）；NL为主信号处左转车道数；tML为主信号处左转车辆排队消散时间（s），由式（16）得到：

（2）左转社会车辆延误

绘制预信号处左转车辆累计到达-离去曲线，如图7 所示，阴影部分为预信号处左转车辆延误。图中折线A'B'C'D'表示预信号处左转车辆到达过程曲线，折线F'B'C'E'表示预信号处左转车辆离开过程曲线，本节不赘述具体过程。

图6 中三角形BFP部分面积与图7 中四边形OA'B'F'、三角形C'D'E'面积之和即为一个信号周期内左转社会车辆总延误。四边形OA'B'F'面积也等于四边形OA'B'G'面积减去三角形B'F'G'面积：

图7 预信号处左转车辆累计到达-离去曲线Fig.7 Cumulative arrival and departure curve of left turn private vehicles at pre-signal

2.4 交叉口通行能力计算

本文采用饱和流率法进行计算交叉口通行能力。文献[7]在分析逆向可变车道通行能力的过程中发现，设置逆向可变车道虽能显著提高左转通行能力，但对通行能力的提高程度受到车辆到达分布及预信号绿灯时长等因素的影响，通常难以实现最大通行效率，所以本文对逆向可变车道的通行能力根据常规车道组通行能力进行折减。

交叉口通行能力按式（23）计算：

式中：Ani,Anj分别为每一进口道常规车道数和逆向可变车道数；λni,λnj分别为各进口道常规车道和逆向可变车道绿信比；n,i,j分别为进口道、各进口道常规车道和逆向可变车道编号；f为折减系数，一般取0.5～1，本文取0.9。

2.5 约束条件

2.5.1 主信号约束

交叉口信号配时参数约束为：

式中：Gp为交叉口各相位有效绿灯时长（s）；p为交叉口各相位编号；L为一个信号周期总损失时长（s）；Gpmax,Gpmin分别为各相位最大、最小绿灯时长（s），最小绿灯时间应满足行人过街最短时间需求；xp为第p相位饱和度。

2.5.2 相位相序设定

本方案采用“先左转、后直行”交通组织思路，主预信号协调配时方案如图8所示。主、预信号配时应满足下列关系：

图8 主预信号协调配时方案Fig.8 Phase plan of pre-signalized intersection based on contraflow left-turn lane

式中：G2,G3分别为第二、三相位绿灯时间（s）；t2为左转预信号绿灯延后开启时间（s）。

2.5.3 功能路段长度约束

本方案中交叉口进口道共分为三个功能路段，分别为综合待行区l1、借道左转车辆渐变段l2以及社会车辆储存段l3，见图1 所示。本节对三种路段的长度约束展开讨论。

（1）综合待行区车道长度l1

本方案中左转社会车辆可利用左转专用道和逆向可变车道通过交叉口，逆向可变车道也可视作综合待行区组成部分，其长度与综合待行区长度相等。关于该路段长度，相关文献[18]对其进行了推算，见式（29）～式（31）：

式中：lS,lL分别表示直行或左转车辆在综合待行区排队长度（m）；hC为标准车辆排队车头间距（m）；λS,λL分别为主信号的直行、左转车道有效绿信比；ω为交叉口一小时内信号周期个数；N为高峰15分钟内每一信号周期左转或右转的排队车辆数。

（2）借道左转车辆渐变段长度l2

该路段可类比于车道展宽渐变段，其长度与车辆最小转弯半径有关。为保证车辆行驶安全，l2应满足城市道路交叉口设计规范[19]，见表1。

表1 进口道渐变段最小长度设置规范Tab.1 Minimum length setting specification for the transition section of the approach

（3）社会车辆储存段车道长度l3

进口道设置双停车线可能导致部分社会车辆二次停车，该功能路段长度应至少满足高峰时期直行或左转社会车辆的排队需求，避免排队车辆溢出。该路段长度与一周期内的社会车辆到达率、车辆排队间距等因素有关，需满足以下条件：

（4）交叉口间距约束

三个功能路段长度之和应小于城市道路两交叉口最小间距l5，即：

2.5.4 预信号约束

（1）直行预信号绿灯提前结束时间t1

在周期结束前，需保证综合待行区内车辆清空，以便直行、左转公交优先行驶到主信号处排队。t1的大小与综合待行区、渐变段长度以及社会车辆平均行驶速度有关，应满足以下条件：

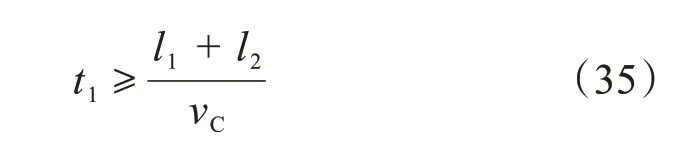
式中：vC为社会车辆在主、预信号之间的平均行驶速度（m/s）。

（2）左转预信号绿灯延后开启时间t2

本方案中，首先放行次要方向上的直行及左转车辆，在考虑交叉口车辆行驶安全的前提下，为充分发挥逆向可变车道功能，应在第一相位最后一个车辆驶过逆向可变车道后，启亮预信号绿灯。同时，应保证第三相位绿灯开启时驶出预信号停车线的第一辆左转车辆可以到达主信号处。t2应满足以下条件：

式中：l4为次要方向左转车辆在交叉口内部行驶的路径长度（m），左转车辆转弯半径一般不小于25 m；Δt为左转预信号绿灯较主信号绿灯提前启亮时间（s），便于左转社会车辆提前驶入前方车道，在公交车辆驶出交叉口后紧随其后排队，该时间设定应满足：

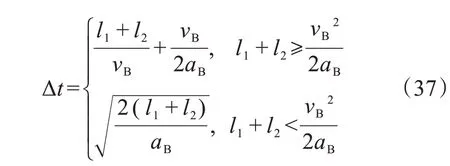
式中：vB为公交车辆在双停车线之间的平均行驶速度（m/s）；aB为公交车辆在双停车线之间行驶的平均加速度（m/s2）。

（3）左转预信号绿灯提前结束时间t3

第四相位绿灯期间，逆向可变车道功能转变为对向出口车道，参考图2（d）。为避免左转车辆与对向直行车辆产生冲突，应提前结束左转预信号绿灯，清空逆向可变车道上的左转社会车辆。该时间主要取决于社会车辆在驶出预信号后的行驶路径长度和平均速度，应满足以下条件：

式中：lW为进口道一条车道宽度（m）；lDY为道路中央双黄线宽度（m）。

2.5.5 求解算法

模拟退火算法是基于蒙特卡洛迭代求解策略的一种随机寻优方法[20]，在解决局部最优和全局最优问题上具有突出表现。模型求解关键在于渐变段长度l2，因其取值有客观依据，为方便模型求解，首先确定l2值。因此，将l1、l3与各相位有效绿灯时间作为变量代入模型。基于模拟退火的交叉口信号控制方案寻优算法步骤如下：

Step 1 设定变量个数narvs，初始温度T0，最低温度Tmin，马尔科夫链长度（即最大迭代次数）maxgen，每个温度下的迭代次数Lk，温度衰减系数a。

Step 3 设计满足约束条件式（24）～式（38）的随机扰动，产生新的变量集x1，得出新解y1。

Step 4 判断y1、y0大小，若y1＜y0，则接受y1作为当前解，进入Step 6，否则进入Step 5。

Step 5 根据Metropolis 准则计算一个概率p= exp( -(y1-y0)/T0)，生成一个（0,1）之间的随机数rand(1)，若此概率大于随机数，则将新解y1作为当前解；否则保留原解y0。

Step 6 进行退火，即T=a·T0，若满足温度下降终止条件T0≤Tmin或已达到最大迭代次数，进入Step 7；若不满足，转至Step 3。

3 算例分析

为验证本方法效果，选取某十字型信号控制平面交叉口进行算例分析。假设某交叉口现状几何布置情况如图9（a）所示，东西向为主干路、南北向为次干路。东西进口道设置有1条公交专用道，南北进口道处无公交通行，其车道功能划分及高峰时期流量分布见表2，算例中公交对社会车辆的当量转换系数为2。按照本方法对交叉口改造后的几何布局形式如图9（b）所示。

表2 车道功能划分及流量分布Tab.2 Lane function division and traffic distribution

图9 算例交叉口优化前后布局形式对比Fig.9 Comparison of layout forms before and after intersection optimization

串联交叉口同样设置有双停车线，且其实现公交优先的控制策略与本文思路相似，所以为验证本方案有效性，将常规交叉口（方案1）、串联交叉口（方案2）与本方案交叉口（方案3）的人均延误、通行能力等指标进行比较。

取交叉口单车道饱和流率为1600 pcu/h，根据美国《道路通行能力手册2010》将每相位损失时间设定为3.2 s，全红时间为0 s，经计算得到方案1 的信号配时方案如表3所示。

表3 方案1相位顺序及信号配时方案Tab.3 Phase sequence and signal timing of scheme 1

3.1 主要参数求解

利用2.4.4 算法在MATLAB 软件中求解模型，将优化模型中的最高温度设为2 000 ℃，最大迭代次数为1 000，每个温度下的迭代次数设为300，温度衰减系数设为0.95。取l2为30 m，lW为3.5 m，lDY为2 m，vc为10 m/s，vB为10 m/s，aB为1.5 m/s2，hc为7 m，PB为30 per/pcu，PC为2 per/pcu，城市主干道两交叉口最小间距为600 m。方案2的信号配时参数根据文献[21]提出的基于串联设计的公交优先信号配时优化方法（见表4），在本文模型中代入相同参数求得。经优化计算，得到本文方法即方案3 的最优配时方案以及各功能路段长度等参数（见表5、表6、表7）。

表4 方案2相位顺序及信号配时方案Tab.4 Phase sequence and signal timing of scheme 2

表5 方案3预信号配时参数计算结果Tab.5 Calculation results of pre-signal timing parameters

表6 方案3相位顺序及信号配时方案Tab.6 Phase sequence and signal timing of scheme 3

表7 方案3各功能路段长度计算结果Tab.7 Calculation results of each functional section length

3.2 延误及通行能力分析

以累计到达-离去曲线法为基础，利用本文模型代入配时参数得到三种方案的人均延误（见表8），再根据式（23）计算得到三种方案的进口道通行能力，指标对比分析如图10、图11所示。

图11 三种方案进口道各流向通行能力比较Fig.11 Comparison of capacity of each direction at three schemes’approaches

表8 三种方案交叉口人均延误比较Tab.8 Comparison of average person delay at intersections of three schemes

图10 三种方案各类型车辆车均延误比较Fig.10 Comparison of average vehicle delay at intersections of three schemes

人均延误方面，本文方案相较于常规交叉口下降了24.3%，与串联交叉口相比下降了11.1%；车均延误方面，本方案与另外两种方案相比，在降低公交车均延误上效果明显。左转社会车辆延误有小幅增加，但影响较小可以忽略。

通行能力方面，本方案与常规交叉口、串联交叉口相比，所有进口道通行能力总和分别提高了32.6%和16.9%，且本方案对直行车道组通行能力的提升效果优于串联交叉口。

3.3 敏感性分析

针对影响本方法算例结果的主要因素：车辆到达率、直行和左转公交车辆在同流向车辆中的占比、功能路段长度等，本节进行敏感性分析，便于选择本方法最佳应用环境。

（1）在车辆到达率方面，取直行公交占比20%，左转公交占比20%，直行与左转车辆到达率分别在0～0.5 pcu/s、0～0.2 pcu/s 内变化，以方案3 较方案1人均延误下降比例作为分析目标，计算结果如图12 所示。由图可知随着车辆到达率增加，本方法改善交叉口人均延误的效果越明显，且本方法对左转车辆到达率更加敏感。

图12 直行和左转车辆到达率对人均延误的影响Fig.12 Impact of arrive rate of through traffic and left-turn traffic

（2）在直行与左转公交车辆在同向车流占比方面，取直行与左转车辆到达率分别为0.35 pcu/s、0.1 pcu/s,公交占比在0～50%内变化，以方案3 人均延误变化为分析目标，计算结果如图13所示。

图13 直行和左转公交占比对人均延误的影响Fig.13 Impact of proportion of through bus and left-turn bus

由图可看出直行公交占比变化对人均延误的影响较小，在直行公交占比较小且左转公交占比较高的区间内方案效果较好，具体表现为左转公交占比30%～35%、直行公交占比20%～25%。左转公交占比减少，方案效果将受到影响。

（3）在功能路段长度方面，对模型进行多次优化计算发现社会车辆储存段长度l3在最优解中的取值范围较广，可预见目标函数对其并不敏感，故选择综合待行区长度l1与渐变段长度l2进行敏感性分析。取直行与左转车辆到达率分别为0.35 pcu/s、0.1 pcu/s,l1取 值70～120 m，l2取 值30～50 m，以方案3人均延误变化为分析目标，计算结果如图14所示。由图可知人均延误与两种路段长度成正比关系，且对综合待行区长度l1更加敏感，故本方案在实际应用中，相关功能路段长度宜取最小临界值。

图14 综合待行区与渐变段长度对人均延误的影响Fig.14 Impact of comprehensive waitingarea and transition section

4 结束语

以十字型信号交叉口为例，基于逆向可变车道设置方法提出一种新型预信号交叉口进口道形式，以公交优先为目的，提出交叉口几何布局、相位设计方案以及主、预信号协调配时优化方法。设计算例验证本方法有效性，结果显示，本文方法能显著降低交叉口人均延误，在提升交叉口最大通行能力方面效果明显。最后，通过敏感性分析得出：随着车辆到达率增加，本方法对改善交叉口人均延误效果越明显；当直行公交占比25%～35%或左转公交占比15%～25%时，应用本方法效果更好；在实际应用中，进口道处的综合待行区、渐变段等功能路段长度宜取最小临界值。综上，本研究为交叉口实施公交优先控制提供了新的思路，但本文未考虑车辆实际到达的随机性，也未考虑逆向可变车道数量对方法效果的影响，未来还需对以上问题展开进一步研究。