基于均值回归的超额价差套利策略研究

章涵

(复旦大学经济学院 上海 200433)

近半个世纪以来，随着计算机科学、机器学习方法、概率论学科、计量经济学的高速发展，证券投资领域的量化分析方法与程序化交易在全球金融市场获得一席之地。量化投资最显著的优势是可以实现投资决策最大程度与投资人主观分离，通过对一、二级市场信息的整合，做出优秀的二级市场交易决策。在理论均衡市场和实际交易市场中，常常有可识别的较大套利空间。然而，随着计算机算力的飞速提高和人工智能、机器学习理论的进一步完善，量化投资存在过于依赖机器学习的问题。知网数据显示，近年来应用于量化投资的机器学习模型与策略数量快速上升。

利用机器学习通常能够实现对训练集(即历史数据)的最好拟合，但仍会带来一定的问题：(1)容易出现过拟合，在测试集中效果不佳。(2)模型过于黑盒，脱离经济学原理，遭遇特殊事件时抗风险能力差。(3)机器学习对算力和时间要求高，限制了交易频率与交易即时性。(4)学习方法大同小异，容易出现量化策略雷同、交易算法近似、逻辑通道重叠，在有利行情下可预估的市场利润被过度瓜分，市场策略的竞赛变为硬件设备的竞赛，现有的稳定性与利润空间受到较大制约。市场对非学习性的交易策略有日益提高的需求。

均值回归在量化投资策略中占有重要地位，均值回归效应一般指当观察的目标量偏离其价值中枢(或均值)较远时，有较大概率向价值中枢回归的趋势。广义均值回归的目标量形式多样，包括单标的的资产价格、双标的的价格差值、一揽子投资组合的价格或差值等形式；均值回归的方式也十分多样，既包括基本面基本不变的短期内价格回归，又包含基本面本身围绕事物客观发展规律上下波动的长期趋势。

本文试图从创新的角度，以均值回归理论为底层逻辑，寻找合适的权重指数，构造符合客观事实的超额价差模型，设计包含带有移动权重的量化交易策略。首先，在实证分析环节，通过对某一标的(本文选取商品期货-螺纹钢rb)2013—2020年的历史数据进行测算，计算其使收益率最优化的参数，并对参数进行横向比较以检验其稳健性。其次，以该参数构建具体化的交易策略，投入2013—2020年的历史数据进行回测计算，并对结果进行分析。最后，在不改变参数的前提下，模拟其在2021年内的收益情况，并进一步评价策略的可行性。

为避免模型的过拟合和策略的失效，本文依次在各个阶段采取了一定的措施。在初步设计模型阶段，从理论出发而非从统计数据出发，在无监督环境下构建模型架构。在获取计算螺纹钢品种的最优参数时，利用Matlab计量工具，通过循环算法以较小或连续的步长计算最优解，通过梯度下降算法并加入噪音模拟其生成过程；通过可视化手段，尽量保证取得参数是全阶段最优而非全局最优(即参数在所有历史阶段原则上不会出现调整倾向)。在历史回测过程中，模拟真实情景，加入一定的滑点和适度的交易失败概率。在真实模拟中，利用开源交易平台，在不改变参数的前提下模拟实际交易，避免理论不可知信息的误用。

1 文献综述

经济学家通过对不同经济领域的实证研究发现了一定程度的均值回归现象，并依据此提出了有效可行的均值回归交易策略。

Gailliot和Henry(1970) 通过对1900—1904年和1963—1967年主要资本主义国家的汇率实证研究中发现并验证，汇率在长期中存在趋稳的特征。但是随后关于汇率均值回归与购买力平价的实证分析受到了质疑。随着计量经济学的发展，Box、George和Jenkins(1990) 通过对非平稳序列的汇率与利率数据进行一次差分后，得到相对稳定的均值和方差，从侧面印证了货币领域的均值回归特征，由此衍生了一系列的外汇CTA策略，出现了许多以中短线交易套利的对冲基金组织，其中包括Winton、Man AHL等知名基金。

Malliaropulos和Priestley(1999)在对以东南亚七个国家或地区的股票市场为主的证券交易市场进行回归分析后发现，其价格指数与收益率存在显著的均值回归现象。Groppdu (2004) 对美国纳斯达克、纽约等交易所的收盘数据进行分析后，得出了相似的结论。基于均值回归理论，投资员开发了和传统布林线动量策略相反的布林线均值回归策略(通过不同的参数和止盈止损条件)。此外，衍生出了收益更有说服力且风险更低的同板块价差均值回归策略、综合三因子模型的大小股市值股价差均值回归策略。

商品期货市场的均值回归似乎是显而易见的：现货价格围绕市场价值均值回归，期、货现货价格互相均值回归，品类间远近期价差围绕0上下波动。由于有较强的逻辑依据，学术界围绕期货市场的均值回归实证研究并不多，但是有较多的衍生策略，其中包括双均线策略(Joseph E.Granville，1962)、反向菲阿里四价策略、网格交易策略、R Breaker回转策略等。商品期货市场由于其市场深度大、兼具标的基本面信息和技术面信息、允许T+0交易和卖空交易(特指国内)等原因，成为各类量化交易策略的实验田。基于技术性原因和法律合规性原因，本文在策略的实证与回测阶段将主要基于我国期货市场进行。

2 理论思路与策略设计

2.1 理论逻辑

均值回归经典逻辑为，当构造标的价格远高于或远低于其价值中枢时，有较大概率发生向价值中枢回归的事件，基本模型为：

其中：D为该标的在期的价格；为均值回归因子参数，为参数。

该式也可写为：

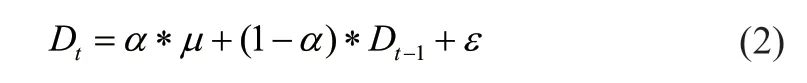
因此，可以理解为，*为价值中枢，(1-)*D为不完全回归部分价格。当均值回归因子＞2时，具有过回归趋势，下期价格通常突破价值中枢压力，且价格不具有收敛趋势；当2＞＞1时，具有过回归趋势，也通常突破但是收敛于价值中枢；当均值回归因子α取1时，期价格D完全回归至价值中枢*，并保持稳定；当均值回归因子取0时，D=D，价格稳定偏离其价值中枢；当取负值时，均值回归趋势不成立，价格远离价值中枢。

迄今为止，主要针对A股、中国期货市场、美股、美国期货市场的实证分析中，或其等价含义的回归因子主要分布于0～1，且显著性水平较高，说明在现实市场中确实存在一定的回归现象。

经典价差回归标的选取为：

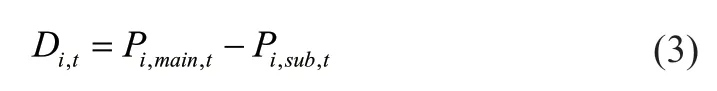
本文选取两资产带移动权重的超额价差作为回归标的：

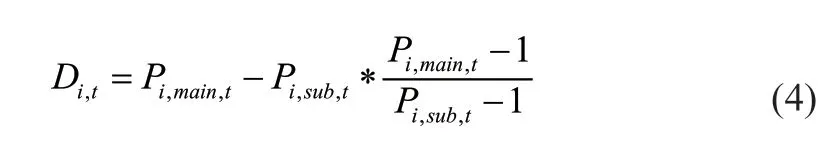
其中：D为标的；P为主资产在期价格；P为次资产在期价格；P为主资产在-1期价格；P为次资产在-1期价格。

本文对原有模型做出了权重的修改尝试，原本的价差均值回归模型经济含义为价差自身的均值回归，两资产完全等权重且为1；在修改之后，引入上一期价格作为当期权重，经济含义演变为动态增长的均值回归。

进行移动的赋权之后，模型表层的经济意义减弱了，价差从直观可视的资产价差变成没有直接意义的价差，但是模型的系统性经济意义增强了，原有价差在一定程度上无视两者资产本身属性的差异，弱化了价格较低资产的变动幅度；修改后适用范围得到扩宽，原本回归标的通常只能用于期货单一品种的价差跨期套利，或一篮子商品的组合跨期套利，现在可以在同类标的不同品种间，甚至是不同品类间实践运用。

从统计学意义来说，带移动权重的价差回归标的更易分布在0的两侧，从而具有更高的平稳性；从实际操作来说，操作难度提高了，为了满足其对应的交易策略，次资产的数量仍然需要和最小交易单位达成最小公倍数，从而对账户的容量、交易手数、市场深度提出了新要求。

移动权重的超额价差均值回归模型的逻辑图如图1所示。

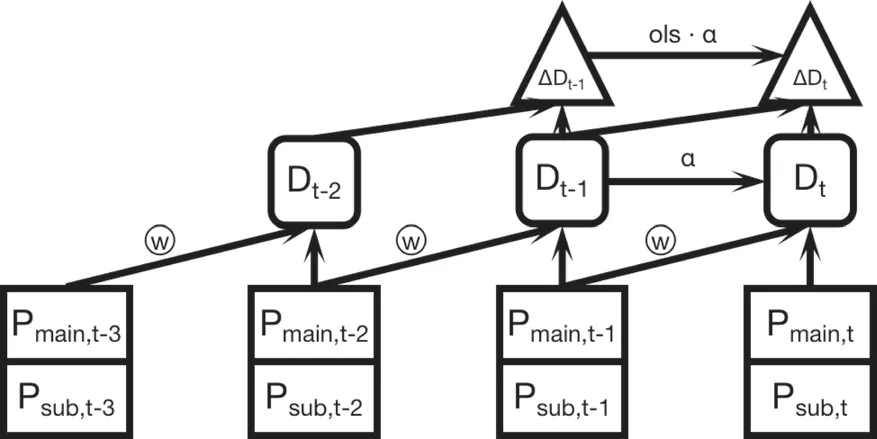
图1

图中，P表示价格；w表示前一期价格以权重形式介入下一期的D中；表示之间存在以为回归因子的相关关系；ols ·表示在经过一阶差分后进行最小二乘OLS回归，得到α估计值。

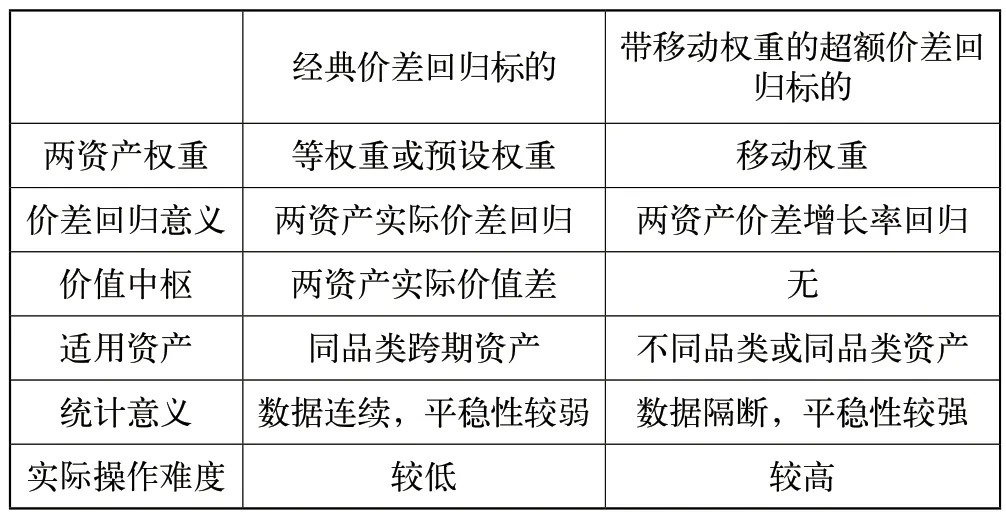
表1

此外，建立适用于交易判断的超额价差套利收益解释模型：

其中，等号左侧的R为资产组合在期的收益，如果在-1期做多1份主资产，做空P/P份次资产，将在第期获得的损益。实际回归中，参数的选取取决于ADF检验中lag order的参数返回。为理论上的收益截距，在长期市场中，均值为0。

由于该模型完全以指导策略开发为目的进行设计，因此等号左侧需要严格保持实际损益水平，且若进行差分，需要实际交易所考虑的残差项、截距项等信息会被忽略，因此纵使该式被解释变量与解释变量均为不平稳，也不进行一阶差分。模型中，假设的交易体量为做多(做空)1单位主资产，同时做空(做多)P/P单位次资产。

根据平稳性分析结果，考虑以较大的lag order值9作为回归的值，即以D至D为独立的自变量，对第期的实际收益(等号左侧)进行多项OLS回归，若能得到显著性水平较高的D项，则可据此开发相应的策略。除了显著性之外，并不关心^2和常数项的显著性水平。

超额价差套利收益模型回归结果符合预期：中高频交易数据中，历史超额价差信息对交易结果具有很显著的负相关关系，中低频交易收益结果对历史超额价差信息同样呈负相关关系。

2.2 策略设计与参数选取

前文显示，可以构建有效的超额价差均值回归套利模型，利用主次合约进行跨期、跨品种、跨币种套利。其中的逻辑是，由于前一期超额价差的系数显著为负，故将在构建量化投资策略时，考虑以前一期带移动权重的超额价差信号做反向操作，且利用显著性次之的前2～5期做协助构建交易信号，进行交易信号的增强或适当抵消。

通过上一部分引入的超额价差均值回归理论，在实际应用中有着复杂的约束条件。首先，融资约束，在我国能够进行合规的卖空操作仅有期货期权交易与融券。其次，交易流动性，融券的长期性和二级市场缺乏显然不适用量化，因此本文将从期货出发进行策略构建和回测展示。最后，交易体量，在理想的交易模型中，交易体量为：

其中，为交易的手数，但是实际上大部分交易不是无限可分的，因此交易体量可等价变为最小公约数下的整数手：

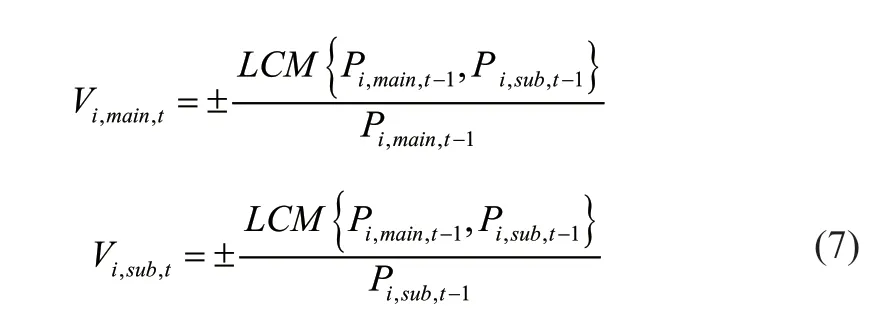
其中，代表最小公倍数，由于现实中资金量的限制和交易深度的限制，将交易手数进一步萎缩为：

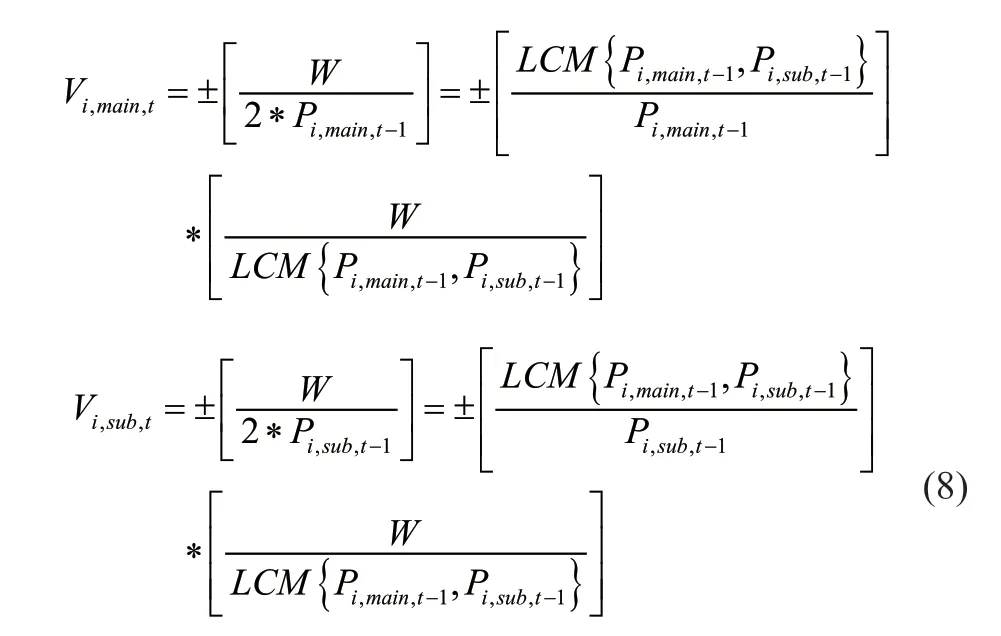
式中，[ ]为向下取整符号，为交易金额，触发交易的条件为：

其中：μ为品种交易中为了稳健或降低手续费的阻尼常数；*为交易调整后的目标仓位(手)；*为交易时的资产总额；为持仓比例，有=W*；，和为非对称的参数；为每手价格；依旧服从于：

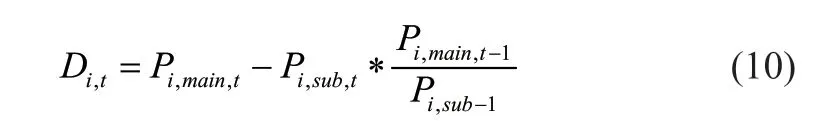
基于此策略逻辑，对目标资产螺纹钢期货进行验算，选定参数(，，)与超参数()。选定参数过程中，在追求收益最大化的基础上，为避免选取的过拟合，遵循三个原则：

(1)参数简单，尽量避免追求历史收益而过拟合。

(2)模型简单，尽量选取使模型结构对称的参数。

(3)全局最优，不仅关注参数的历史总收益最高，还尽量选取全程相对最优。

最终，根据2013—2020年的历史高频(5min)与低频(1day)数据，选定最终交易策略为：

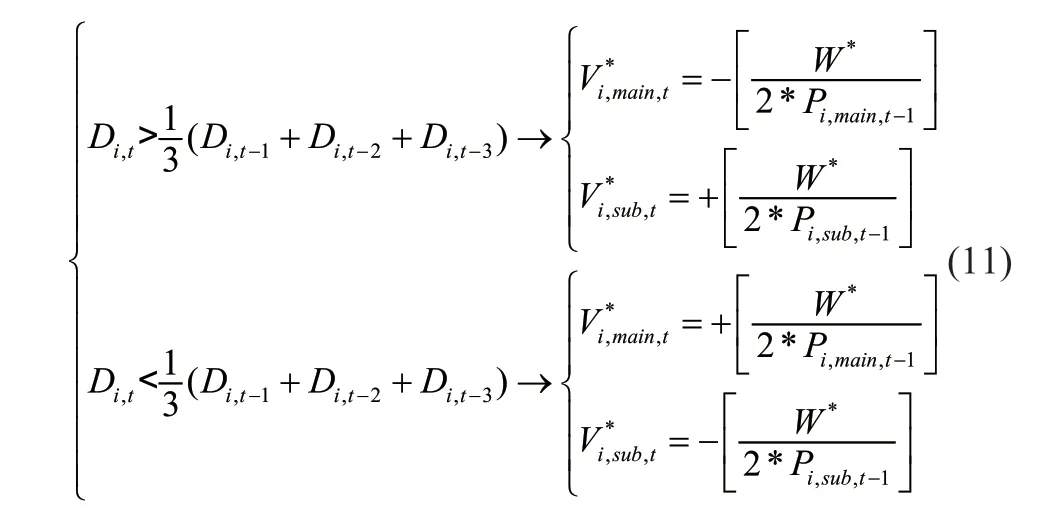
结果最优的模型中，阻尼常数萎缩，历史权重趋同于1/3，在不具有额外效用假设下，最优几何均值的持仓比例趋向1。策略的文字性描述为，逐期测算前三期的超额价差的平均数，并根据当期的超额价差与其大小关系，若当期大于前三期平均，则做空主资产(螺纹钢主力合约)，持有次资产(螺纹钢次主力合约)；若当期小于前三期平均，则持有主资产，做空次资产，几乎不存在空仓位情况。

3 实证与回测

3.1 数据选取

本文对模型的实证分析与回测将从螺纹钢期货rb的主力合约与次主力合约出发，分别研究其中高频与中低频的模拟交易。

期货数据由上海期货交易所给出，以主力合约作为主资产，以次主力合约作为次资产。中高频数据选择2013年1月4日09：05—2021年10月15日15：00所有的五分钟数据，取每个五分钟bar内收盘价作为价格，取买一价卖一价均值作为统一价格。尽管涉及休日与隔夜，但出于对实际交易策略指导的目的，不对隔夜价格进行前后复权操作，即对隔夜数据当做连续数据处理。2014年12月26日及其后上期所螺纹钢品种增设夜市，同样按照连续数据处理；法定节假日闭市，缺省值直接剔除处理。中低频数据选择2013年1月4日—2021年10月15日所有开盘的日数据，不考虑夜盘，取每日14：59收盘价买一价与卖一价均值作为价格，同样将法定节假日直接跳过。此外，由于期货存在主次合约交替的问题，因此根据每日持仓量与交易量(以上期所公布数据为准)滚动选取主合约与次合约，当主次合约发生交替时直接衔接，不做前后赋权处理。

整个实证与回测分为两部分组成，历史回测部分采用2013—2020年数据，不考虑交易是否能被市场深度吸纳，采用统一价，不考虑买卖价差；真实回测部分采用2021年内数据，利用AutoTrader回测平台，抓取模拟真实交易场景下客观存在的可交易对手挂单价(并非成交价)与挂单量，具有更强的现实意义。但是由于真实回测数据点较少，不进行中低频的日频回测，且全程不调整系数。如表2所示。

表2

3.2 历史回测

历史回测过程采用Matlab自编写的回测程序进行。

针对现实交易中的摩擦现象，本文采用跳点形式进行模拟，分别引入0跳点、0.5跳点、1跳点、1.5跳点、2跳点进行稳健性测试。为了应对现实中较高的交易摩擦，选择在交易间引入一定的step区间，即程序判定的交易周期，以降低发生交易的频率。区间分别考虑10倍运算周期(50min)、20倍运算周期(100min)、50倍交易周期(250min)、100倍交易周期(500min)。历史回测结果如图2所示。

由图2可以看出，当市场摩擦较小，深度充足的情况下，较短的交易周期有着明显更好的收益情况，而较长的交易周期在大部分情况下都表现出较好的稳定性。

图2

针对交易周期250、1跳的回测进行描述性分析，如表3所示。

表3

结果显示，胜率69.48%并不算特别优秀(明显低于一些机器学习的结果)，但是夏普比率、年化收益率、最大回撤相对可观。因此传达的信息是，在该策略下，并不能非常准确地识别交易方向，但是可以有效地把握交易时机，通过“赢大输小”赚取稳健的利润。

3.3 真实回测

真实回测阶段，利用AutoTrader回测平台进行可执行的交易模拟。由于在模拟过程中采用了市场中可得的卖一价与买一价、卖一量与买一量进行计算，此时的策略模型有一定修改，交易量由于受到深度影响，将根据主次合约中可得的交易量更小的一方决定目标仓位。虽然已经包含实际数据，但是为了模拟在交易过程中可能出现的网络延迟情况，出于稳健考量，依然引入2个跳点进行模拟。历史回测结果如图3所示。

图3

且有交易指，如表4所示。

表4

没有统计胜率是由于在交易中，由于价差套利的性质，平台给出的胜率数据包含了一多一空的组合，几乎处于50%。通过观察发现，该策略与市场走向关系极小，不受大宗商品整体市场的涨跌制约，同时适合在波动市场与单边行情采用。模拟结果显示，在真实回测中，相比历史回测有着明显更优的收益情况，可能是由于历史回测相对高估了交易的摩擦与损失(对滑点做了单边假设)；回撤数据明显差于历史回测，仅在一年中就超过了原有的最大回撤1%，说明该策略值得在更长的时间段进行真实回测的检验。

4 结语

随着学习类策略的大量采用，机构的量化决策者逐渐重新重视“先决知识少、欠拟合”的简单模型策略。本文在此诉求的基础上，试图通过表层的市场规律进行一次量化策略设计。

为了最大程度地达到避免巴菲特说的“看着后视镜开车”过多后验信息介入模型建立，本文做出了许多努力，这些努力也为最终模型的效果做出了贡献：

(1)根据历史数据选定简单、稳定的超参数。

(2)复杂模型到简单策略的萎缩过程中尽量采用对称参数。

(3)选取参数尽量关注全局曲线而非最终值。

(4)采用较大的模拟跳点。

(5)在复杂的真实回测中采用可得的交易数量与价格，而非简单采用统一价。

此外，由于策略“一多一空”的架构设计，极少会面对极端风险，但是仍需要对可能出现的单边爆仓做出一定的风险管理。由于交易的连续性质和出于节省手续费考虑，可以视本策略为连续策略，而不像一般日内策略需要在收盘时平空仓位。

值得一提的是，由于合规的需要，本文策略的回测建立在螺纹钢期货的基础上，但是并不代表该策略有这方面的局限。读者在复现或付诸实践的过程中，可以考虑将该策略嫁接于外汇交易、虚拟货币交易等领域内：

(1)外汇交易具有可分割性强的特点，能更好地执行移动权重下仓位控制的策略优势。

(2)外汇交易中货币间的价值量由第三方的隐含汇率确定，因而在这种主次资产真实价值悬殊的市场中，更能发挥本策略权重灵活的优势。

(3)外汇与虚拟货币市场深度远超期货市场，目标价格更可得，交易摩擦更小。

(4)虚拟货币市场还具有连续性好的特点，且对量化交易者等交易量大的还有较大的费率优惠。

本策略在研发过程中，在外汇与虚拟货币的历史回测、真实回测、实盘交易中均取得了较好的效果，在回撤极小的情况下，构建增长迅速且平稳的收益曲线。