Polynomial-Time Assignment-Based Cell Association with Generic Utility Functions

Lusheng Wang,Chao Fang,Hai Lin,Min Peng,Caihong Kai

1 Key Laboratory of Knowledge Engineering with Big Data,Ministry of Education.School of Computer Science and Information Engineering,Hefei University of Technology,Hefei 230601,China

2 Key Laboratory of Aerospace Information Security and Trusted Computing,Ministry of Education.School of Cyber Science and Engineering,Wuhan University,Wuhan 430072,China

Abstract: Cell association is a significant research issue in future mobile communication systems due to the unacceptably large computational time of traditional schemes.This article proposes a polynomial-time cell association scheme which not only completes the association in polynomial time but also fits for a generic optimization objective function.On the one hand, traditional cell association as a non-deterministic polynomial (NP) hard problem with a generic utility function is heuristically transformed into a 2-dimensional assignment optimization and solved by a certain polynomial-time algorithm,which significantly saves computational time.On the other hand, the scheme jointly considers utility maximization and load balancing among multiple base stations (BSs) by maintaining an experience pool storing a set of weighting factor values and their corresponding performances.When an association optimization is required, a suitable weighting factor value is taken from the pool to calculate a long square utility matrix and a certain polynomial-time algorithm will be applied for the association.Comparing with several representative schemes, the proposed scheme achieves large system capacity and high fairness within a relatively short computational time.

Keywords: mobile communication system; 2-dimensional assignment problem; hungarian algorithm;fairness;cell association

I.INTRODUCTION

With the integration of femtocells and traditional macrocells, wireless networks evolve toward heterogeneity making their resource allocation a more and more critical issue [1].Femtocells may bring in an augmentation of the system capacity,but the difficulty for associating user equipments (UEs) with base stations(BSs)becomes more severe especially if the network densification is high,i.e.,evolving toward ultradense networks [2].Cell association is to associate each UE with a particular serving BS,which substantially affects the performance of the whole network[3].To find a fast cell association scheme for future networks is important,and the primary feature should be low time cost.Besides, it is better to consider the tradeoff between multiple metrics while existing optimization solutions optimize mainly one single objective and are not flexible for usage.

In the literature, there are plenty of research works on cell association.A typical scheme is to consider a single traditional performance metric, such as signalto-interference-plus-noise ratio (SINR) [4].If transmission power between a femtocell and a macrocell is considered as a key factor,too many UEs may choose the macrocell, so this kind of association schemes’performance in terms of system capacity or fairness may not be high although they may quickly reach an association.To find a suitable scheme, many studies tried optimization and game theory.The problem was transformed into a distributed convex optimization in[5]and an alternating direction method was proposed to solve it.The scheme tended to associate a lot of UEs to underloaded femtocells for load balancing.A UE behavior awareness based scheme was proposed in [6], whose association result was mainly decided by the match between instantaneous states of all the UEs and the characteristics of BSs.The authors in[7]transformed the problem into a convex optimization by relaxing the binary variables into continuous ones,and solved by the Lagrange duality method.A cell association scheme was proposed in[8]which continuously learned UE behaviors and dynamic UE environment by online Q-learning.Thus, load balancing was improved by guaranteeing the quality of service(QoS) of some UEs far from any BS.The authors in[9] achieved the optimum by guaranteeing the downlink UE QoS using a deep Q-learning based scheme.Internet of things(IoT)applications and high-capacity backhaul for small cells were studied in[10],the problem was modeled as a non-linear integer programming and a heuristic algorithm was proposed for minimizing the downlink network delay.

Many game-based schemes were also proposed in recent years.A non-cooperative access game between BSs and UEs was studied in [11] to improve the system throughput,where the leaders estimated the strategies of their followers to decide on their strategies and the followers did the best response to the leaders.Some studies applied matching game theory for cell association and distributed algorithms were proposed.In[12],matching game was used to converge to a local optimum for queue-aware traffic offloading.In [13],matching game was used to solve the multi-objective optimization which modeled the dissimilar association requirements for IoT and human-to-human coexisting networks.Multi-armed bandit game was used to model the multiclass cell association problem in[14].A distributed user-driven algorithm focusing on two similar classes of devices as the above reference was proposed, which converged to the equilibrium.The distributed user association problem for energy harvesting was studied in[15]and an approach based on mean-field multi-armed bandit game was proposed.

Some studies jointly considered cell association with other resource allocation aspects.The authors in[16]jointly studied cell association and power control by simultaneously optimizing system total utility and power consumption.The problem was modeled as a mixed integer convex optimization and solved by an annealing-based coalition game and the primal decomposition theory.The joint optimization of cell association and content placement was modeled in[17]as an integer nonlinear programming problem.Lagrangian partial relaxation and McCormick envelopes methods were used to transform it into an assignment problem and two linear integer programming problems,which could be solved by low-complexity methods,such as the Hungarian algorithm.Assuming that contents were placed in advance,the joint optimization of cell association and BS resource allocation was modeled into a mixed integer nonlinear programming in[18] and a distributed relaxing-rounding method was raised to approach the optimal solution and to improve the cache efficiency.A theoretical framework for energy-delay tradeoff jointly considering BS sleeping and cell association was developed in [19].An M/G/1/N processor sharing vacation queueing was introduced and the optimal association radius was investigated to achieve a tradeoff.The joint user association and wireless backhaul bandwidth allocation problem was studied in [20] and a distributed optimization algorithm based on primal and dual decompositions was proposed to improve system throughput.The authors in [21] studied the joint optimization of user association and subchannel allocation.The global optimum was derived based on graph theory and a local optimum was obtained by an alternative solution.The joint optimization of user association and resource allocation was modeled as a linear programming problem in [22], and the study showed that the optimal user association was determined by a rate-biasing rule with each BS having a specific bias value.Moreover, cell association was also jointly studied under the circumstance of some popular techniques,such as non-orthogonal multiple access (NOMA) [23], massive multiple-input multiple-output(MIMO)[24],and energy harvesting[25].

Besides the above studies,some studies transformed the problem into an assignment problem solvable by polynomial-time algorithms.In [26], cell association and almost blank subframe (ABS) ratio was jointly modeled into combinatorial optimization.Given an ABS ratio,Hungarian algorithm matched UEs and virtual base stations(VBSs),and a strategy toward a relatively small ABS ratio was finally obtained.A VBS idea was considered in[27]to transform the problem into a 2-dimensional assignment optimization where each BS was mapped into multiple VBSs and the UEs were associated with VBSs.The cell association problem with BS dormancy was jointly optimized in[28] and a utility function obeying proportional fairness was considered.On the one hand, cell association was transformed into a 2-dimensional assignment optimization and solved by the well-known Hungarian algorithm.On the other hand, an algorithm with low complexity was proposed for joint optimization based on a successive approximation method.The authors studied the cell association problem by deep Qlearning in[29]and a scheme was proposed to quickly obtain an association strategy for the scenarios with the same UE distribution and BS locations.The authors also studied previously the issue by maximizing the system capacity and proposed a heuristic scheme with an intuitive design of the utilities for associations between UEs and VBSs[30].However,the design was not theoretically supported and extensive performance evaluation was still required.

Seen from the above summary of the related work,most existing cell association schemes are not polynomial, and some polynomial-time schemes are only designed for a specific objective function, such as proportional fairness.Therefore, although there exists many studies on cell association, it is difficult to find a suitable solution that is fast enough.For the sake of time complexity and design universality, this paper proposes a fast polynomial-time cell association scheme that uses a generic utility function as the optimization objective.The main contribution of this study is to heuristically transform the non-deterministic polynomial (NP) hard cell association problem with a generic utility function into a 2-dimensional assignment optimization,so that polynomial algorithms such as Hungarian algorithm can be used to quickly solve it.We seriously analyze the conditions when a many-to-one assignment problem with a proportional-fair utility can be transformed into a 2-dimensional assignment problem.A weighting factor in the scheme is designed to adjust the impacts of utility and fairness.Then, representative weighting factor values and their corresponding performances were stored in an experience pool.For making an association decision, a suitable factor value is taken from the pool to calculate the utility matrix and the Hungarian algorithm is applied to obtain a final association decision.The advantage of the proposed scheme is twofold.On the one hand, its complexity is low and each cell association decision requires a polynomial computational time, but UE fairness and system capacity are guaranteed.On the other hand,the applicability of the scheme is quite wide, such as generic utility function for plenty of optimization objectives,suitability for both heterogeneous and homogeneous networks, unaffectedness by duplex mode, computational capability, and interference management technique of a mobile communication system.

The remainder of this article is organized as follows.Section II defines the optimization problem in the system model.Section III explains the transformation of the problem into a 2-dimensional assignment optimization and describes the proposed scheme.Section IV shows extensive simulations on heterogeneous and homogeneous networks and compares with several existing schemes to demonstrate the performance of the proposed scheme.In the end, the study is concluded in Section V.

II.SYSTEM MODEL

The network studied in this paper is composed of many macrocells and femtocells, denoted by BS ={BSj|j=1,...,N}, whereNrepresents the number of BSs in the region.UEs are represented by UE ={UEi|i=1,...,M}, whereMis the number of UEs.The cell association problem is modeled as an optimization in terms of system utility,given by

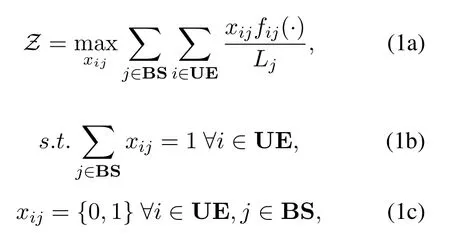
wherexij={1,0}is a binary variable representing the association betweenUEiandBSj.We assume that each UE can only associate with a single BS, sorepresents the total number of UEs associating withBSj.fij(·) is a generic utility function describing the utility of the link betweenUEiandBSj, which is known as prior knowledge before association.Taking the maximization of the system’s total capacity as an example,fij(·)becomes

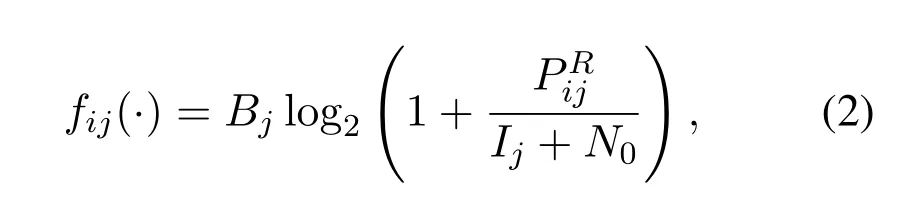
whereBjrepresents the bandwidth ofBSj, andN0is the power of the additive white Gaussian noise(AWGN).Note that (2) does not represent the capacity ofUEidue to the fact thatBjmultiplied in front of the logarithm is the total bandwidth of the BS.To represent the capacity ofUEi, the total bandwidth in(2) should be divided byLjas in (1a), indicating the sharing of bandwidth among the associated UEs.BothBjandLjare known by the BSs, soBj/Ljfor each UE can also be obtained for the optimization process.If (2) is taken into the objective function, bandwidth allocation can be jointly considered with cell association.Intuitively, the division byLjin (1a) averagely shares the total bandwidth of each BS by all the UEs associating with it.Actually,UEs could obtain different amounts of bandwidth if a simple transformation is taken to virtualize the UEs.We assume that each UE has a certain strength value for obtaining resources.For example, if the strength ofUExis twice as that ofUEy, the former can be treated as two virtual UEs of the latter.Thus, the problem is transformed into a 2-dimensional assignment problem,while the scale of the problem is increased from the number of UEs to the number of virtual UEs.represents the reception power for the link betweenUEiandBSj, calculated by

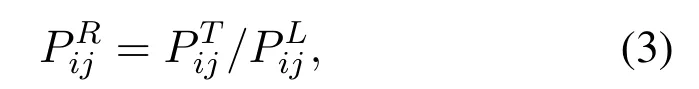
whereis the transmission power, andrepresents the combined effect of path loss and shadowing.A cell association scheme may run periodically but the period should not be too short,otherwise reselection and handover among BSs become excessively frequent.Therefore, small-scale fading is not combined into the model and their effect is not supposed to be considered in the following scheme design.We assume that each UE has given uplink/downlink transmission power values, which should be determined before the optimization in (1).If the transmission power of each UE has a certain interval for flexible optimization, the optimization modeled by (1) is obviously unable to be transformed into a 2-dimensional assignment problem anymore, so power allocation is assumed to be completed before cell association optimization.In other words, a totally flexible joint optimization of power allocation and cell association is not suitable for the design in the following section.In a real network,the cell association scheme should know,instead of,through channel estimation.Ijin(2)indicates the total interference from the other cells,written as

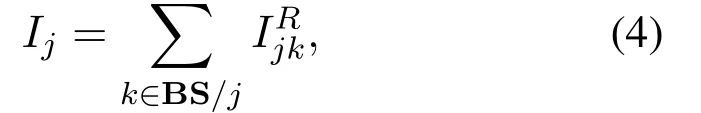
whererepresents the interference from cellkto cellj.Similar to,the interference may also be obtained through channel estimation in a real network.In a theoretical study,the calculation ofis different for uplink and downlink.For the former, it contains the interferences from UEs in adjacent cells toBSj,while for the latter, it contains the interferences from all the other BSs toUEi.Therefore, the association results obtained based on uplink and downlink utility metrices may be also different.Associations may be determined by combining uplink and downlink utilities, or traffic loads in uplink and downlink may employ different BSs.Besides, the employed interference cancellation technique also affects the calculation of the total interference.For example, if the interference from an adjacent cell is cancelled by coordinated multi-point(CoMP)or NOMA,it is not contained into the above total interference.However,these issues do not affect our scheme design, so they are not considered in this study.

III.THE PROPOSED CELL ASSOCIATION SCHEME

3.1 Problem Transformation

The problem modeled by (1) is a typical assignment issue where each UE can associate with one BS but each BS can serve multiple UEs.If the objective function is in a proportional-fair form,this problem can be solved in polynomial time [27], otherwise the problem is not polynomially solvable from the mathematical perspective.For this reason, a heuristic method transforming approximately a generic one-to-multiple assignment problem into a 2-dimensional assignment problem should be interesting, so we design such a scheme in this paper using a VBS concept from[28],which can be finally solved by polynomial-time algorithms,such as Hungarian algorithm.

A VBS is a virtual BS representing the association capability of a real BS during the assignment optimization procedure.Each BS is mapped intoMVBSs while each VBS can only be associated by a single UE.Thus,as shown in Figure 1,the problem may be transformed into a 2-dimensional one-to-one assignment problem between UEs and VBSs.Lines in the left part represent the associated links between UEs and BSs,and symbols denote these links’ utilities.Similarly,spotted lines in the right part represent the associated links between UEs and VBSs,and symbols denote the virtual utilities of these virtual links.denotes the virtual utility for associatingUEiwith thelth VBS ofBSj.

To guarantee an equivalent transformation by the VBS method, three conditions should be satisfied.Condition 1: the utility of the association between a BS and all its UEs should be the same as the summation of the virtual utilities between these UEs and its VBSs.As shown by Figure 2,we havef1j(·)+f2j(·)+f3j(·) +f5j(·) =forBSjandf41(·) =w141forBS1.Condition 2:should monotonously decrease with the increase ofl.This is because the optimization algorithm, such as the Hungarian algorithm,always chooses the BS with a larger utility in priority for each UE.Condition 3:should be an expression only related toUEi,BSj,and thelth VBS.Since it is used to construct the input matrix of the maximization procedure, all theshould be known values before the procedure starts.However,if anyis also related to other UEs’associations,it is unable to be obtained before association decisions,which is really a self-contradictory problem.

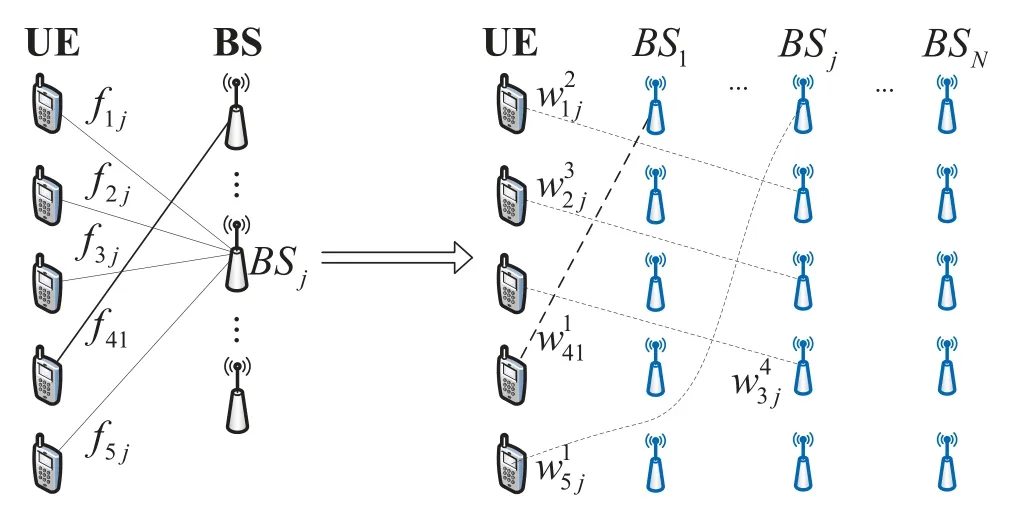
Figure 1.An example of transforming from associations between UEs and BSs to associations between UEs and VBSs.

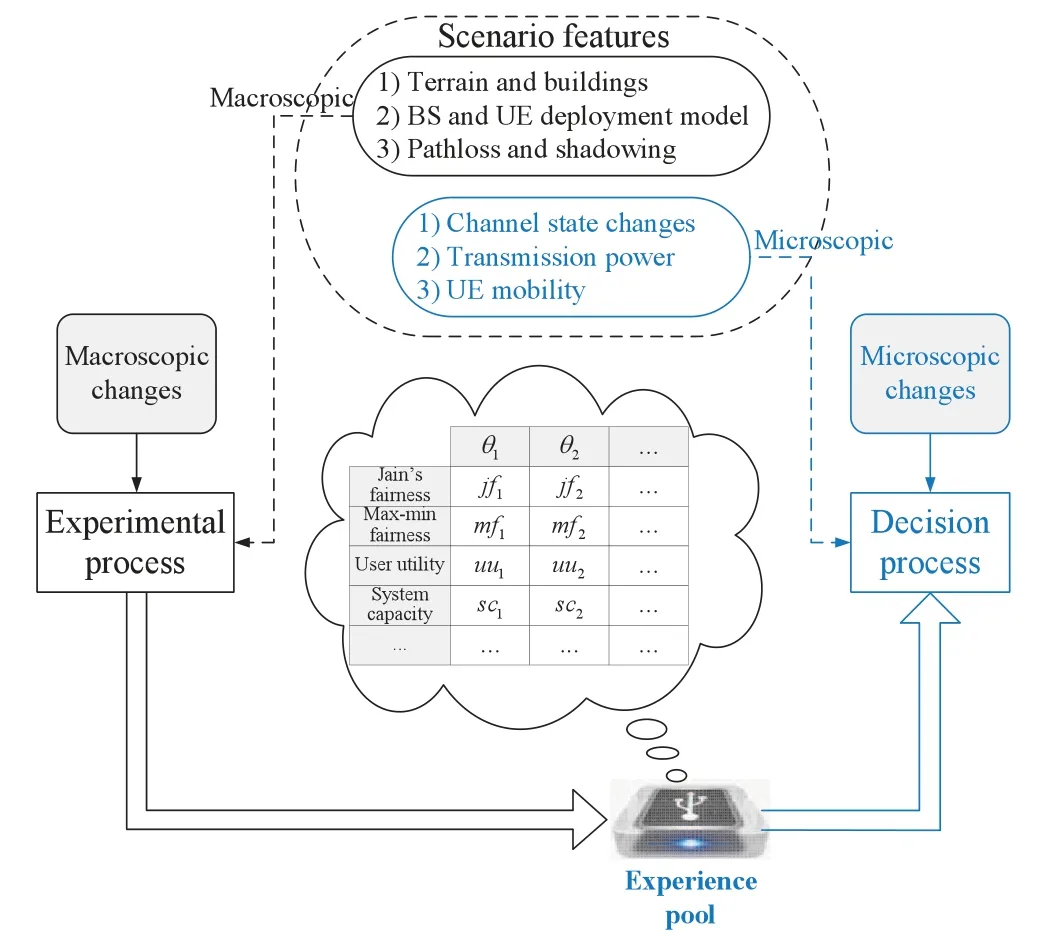
Figure 2.Structure of the proposed cell association scheme.

To the best of our knowledge, the cell association problem with a generic objective function is a common NP-hard problem, which cannot be transformed precisely into a 2-dimensional assignment problem or solved polynomially in mathematics.In other words,it is difficult to find a transformation method fitting for all the three conditions above.However, it is possible to design a heuristic scheme to approximate problem (1) and find a relatively good association result,although a heuristic design brings in a loss on the optimality.Referring to our study in[30],a factor is constructed as

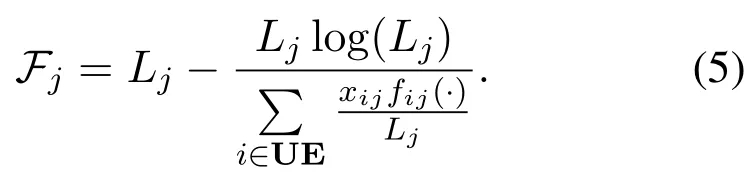
By multiplyingFjon the original objective function in (1), it is transformed into a 2-dimensional assignment issue with the following objective function:

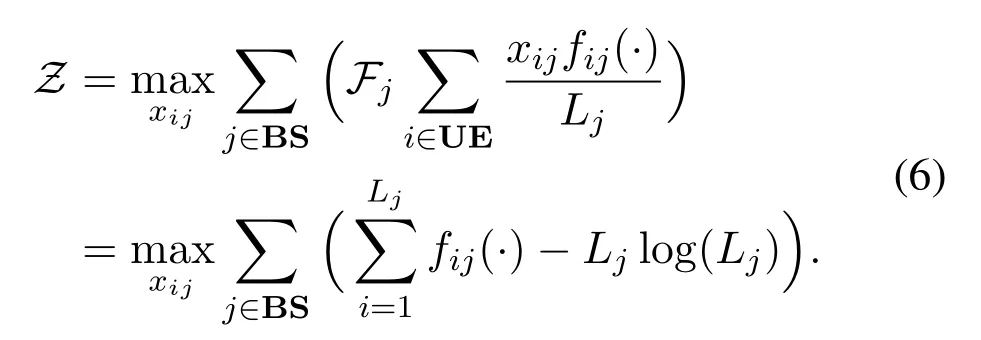
We can see that the effect ofFjis the same as the proportional fairness concept which takes the logarithm on the utilities of UEs in the objective function[31].Since the objective function becomes different from (1) anymore, a constant valueθis inserted to make(6)approximating(1),changing the factor into

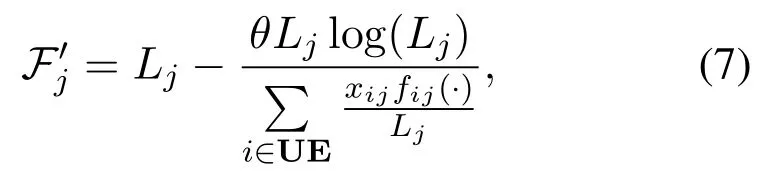
whereθplays a role of a weight on the tradeoff betweenfij(·) and the effect ofLj.TakingF′jinto the original objective function in (1) and considering theLjUEs associating withBSj,we obtain

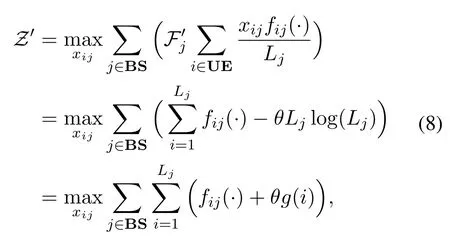
where

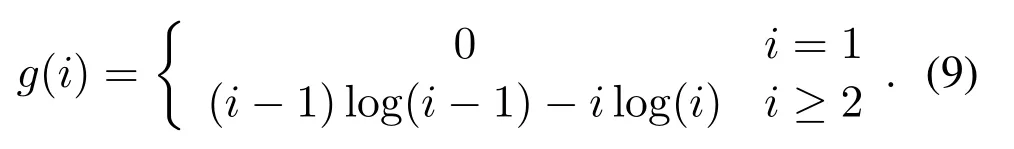
Note that, by summing upg(i),i= 1,...,Lj, most of the parts are eliminated and the last part in the 2nd line of (8) is obtained.Seen from (1) and (8),Ljis always on the opposite of the summation offij(·),so the objective function can be considered as a tradeoff between utility and fairness.The part withLjrepresents a certain level of fairness because it is maximized when the UEs are averagely assigned to the BSs.Whenθ= 0,F′j=Lj ＞1.Whenθ= +∞,F′j=-∞＜1.Sinceθis continuous,there is surely aθmakingF′j= 1.Meanwhile, for a cell association result considering both utility and fairness,all theLj,j= 1,...,Nare usually close to one another for the reason as follows.As we know,UEs and BSs may be assumed to obey certain random point processes,so the numbers of UEs under the coverages of different BSs are usually not far from one another.For a scheme emphasizing UE fairness,the numbers of UEs finally associating with different BSs become further similar to one another, i.e., all theLj,j= 1,...,Nare not far fromM/N.To sum up, we could find aθ ∈[0,+∞) making all theF′j,j= 1,...,Nnot far from 1, so the obtained total utility approximates the summation offij(·) in (1).Although the above analysis does not provide a rigorous proof, it shows the intuitive rationality of our design.

To bring in the VBS concept, we should define a new variablerepresenting the association betweenUEiand thelth VBS ofBSj,i.e.,= 1 if they are associated and 0 otherwise.We know that,should be defined as a monotonously decreasing function ofl,so theLjUEs should associate with the firstLjVBSs ofBSj.Meanwhile, each UE associates with a single VBS, so theLjbinary variables equaling 1 arefor a givenj.Therefore, the above objective function is rewritten as

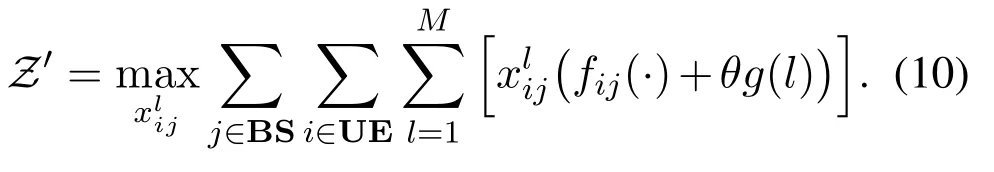
The above formula is a typical form of a 2-dimensional assignment problem, which is the maximization of the total utility(i.e.,the total virtual utility in this problem).in this typical form is a binary variable representing whether taskiis assigned to workerj(i.e.,whetherUEiis associated withBSjin this problem),and the part in the bracket behindshould be the utility of taski.Therefore, the virtual utilityin this problem satisfying the three conditions for transformation is found,written as

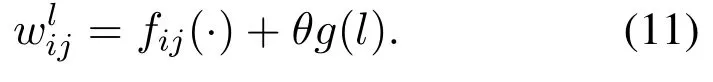
To further understand (11) intuitively, let us check some representative values forθ.Whenθ= 0,in(11)is determined byfij(·).Thus, UEs all choose their most suitable BSs corresponding to the highest summation offij(·),causing load imbalance and very poor fairness.Along with the increment ofθ,the impact of the second part in(11)becomes more and more serious,and that fromfij(·)gradually decreases,making it not so different by associating with different BSs.Whenθbecomes large,is mainly determined by the second part in(11).Although UEs are usually distributed asymmetrically in the whole region, they tend to be assigned to all the BSs on average, which guarantees fairness and load balancing feature among BSs.In a word,θ=0 andθ=+∞are two extremes of considering onlyfij(·)and of balancing the assignment,so there should exist aθthat balances them.We can see that, forθ ∈[0,+∞), the sense of fairness achieved by our scheme is similar to the well-knownα-fairness concept in the literature [31], but the two are not precisely the same.Taking (2) as an example of the utility,α= 0 corresponds to the maximization of system capacity,butθ=0 corresponds to the maximization of a summation of spectral efficiency ignoring the division of bandwidth in(1).

Based on the designedin (11), problem (1) is heuristically transformed into a 2-dimensional assignment problem as follows:

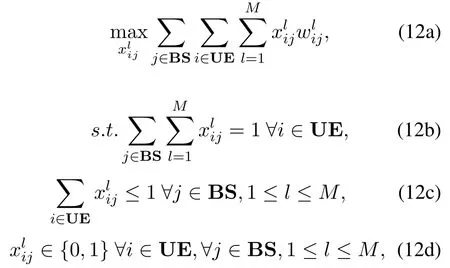
where (12c) represents that each UE should only associate with one VBS, and (12d) represents that each VBS can serve at most one UE.

3.2 An Assignment Scheme for Fast Cell Association

The problem transformation in the above subsection provides the theoretical support for designing a new cell association scheme.A cell association scheme may be performed in a distributed way by each UE to select its most appropriate BS, also known as cell selection in the research field.Meanwhile,it may also be performed by each macro BS to optimize the associations between UEs and BSs(including the macro one and the femtocells)within the coverage area of the macro BS.Our scheme belongs to the second category,so the following designed scheme should be processed by each macro BS based on the locally gathered channel features.Channel conditions of all the links between UEs and BSs in the coverage area may be obtained by the channel estimation procedure and shared to the macro BS through X2 interfaces.A key point in the designed scheme is to quickly choose a suitableθbefore decision making.In a real network,the scheme initially has no experience on the most suitableθvalue, so it has to collect experience from simulations to master and record the relationship betweenθand the network performance in the constructed network environment.Performance metrics here may contain system capacity to be guaranteed, fairness of UEs, link quality of cell-edge UEs,load balancing requirement among BSs,etc.To reach an optimized cell association, the network-side entity(e.g.the operator)should give a clear demand on the performance in terms of the above metrics.An experience pool is used to store the correspondence betweenθand the performance.Given a demanded performance,a correspondingθshould be found from the pool.Therefore,a number ofθvalues should be considered because the precision toward the demanded performance can be improved by storing an amount ofθvalues with a high resolution in the pool.We suggest using a lowθresolution at the beginning of the scheme implementation so that cell association decisions can be timely made.Then,moreθvalues can be gradually inserted into the pool to reach a high resolution.This is also an effective way to implement the scheme in a network with low computational capability.

Based on the above analysis, an assignment-based cell association scheme is proposed in Figure 2,which contains an experimental process and a decision process.The former is preprocessed to construct and update the experience pool, whose process is shown in algorithm 1.It can be triggered by any obvious change of the scenario’s macroscopic features,such as terrain and buildings, BS and UE deployment models, path loss and shadowing,etc.The algorithm firstly forms a simulated network according to the scenario’s macroscopic features.Then,it maps each BS intoMVBSs,and the long square matrix W is calculated.In the end, Hungarian algorithm is applied on W to obtain the association results.

Algorithm 1.Experimental process.Input: Macroscopic features of the scenario;Output: Experience pool;1: for Simulation rounds do 2: Deploy BSs and UEs in the simulated region;3: for θ do 4: Map each BS into M VBSs;5: Calculate the long square matrix W for the given θ;6: Apply Hungarian algorithm for association;7: Evaluate the performance for each metric;8: end for 9: Record the performance for one deployment;10: end for 11: Average performance for each metric and each θ to update the experience pool.Algorithm 2.Decision process.Input: Microscopic features of the scenario, performance demands;Output: Association result;1: Take a corresponding θ from the experience pool for given performance demands;2: Calculate W;3: Apply Hungarian algorithm on W to obtain the association.

W is anM-by-MNlong square matrix,composed of a number ofM-by-Mutility matrices, each of which contains the virtual utilities of associations between all the UEs and all the VBSs of one BS.DenotingW(x,y) as the entry of thexth row and theyth column of W,we have

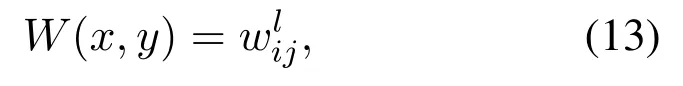
wherei=x,j=yceilM,l=ymodM.

Finally,the performance of various metrics is calculated for eachθstored in the experience pool.Since this pool is determined by the macroscopic features of the scenario, algorithm 1 is processed to update the pool only when it is triggered by an obvious change.Although this algorithm has a high complexity,it does not affect the computational time for real-time decisions on associations which are actually determined by the decision process(i.e.,algorithm 2)as follows.

The purpose of the decision process is to quickly obtain an appropriate association.It can be triggered by an obvious change of the scenario’s microscopic features, such as the variation of some UEs’ channel states,transmission power changes,and the movement of some representative UEs.In the decision process,aθvalue is firstly taken from the pool to match the demanded performance.Then,(11)with the takenθis used to construct W.In the end,Hungarian algorithm is applied on W to obtain the associations between VBSs and UEs.Since we know the BS from where each VBS is mapped, it is easy to obtain the association between the real BSs and the UEs.

Note that,the reception power of useful signals and interferences in the experimental process are different from those in the decision process.For the former,they are calculated based on the simulated channel model and the positions.For the latter, they are real useful signals and interferences evaluated from the real links between BSs and UEs.

IV.PERFORMANCE EVALUATION

When the construction of 5G is launched, femtocells may not be densely deployed at the beginning, so macro BSs should be still the main bearers of traffic loads, forming a heterogeneous network.Along with the construction of more indoor infrustructure,femtocells gradually become dense, which will be used to afford most traffic loads.Thus,the macro BSs may be free of traffic loads and used only for network management,forming a homogeneous structure for traffic loads.Since the 5G network is still under construction and the femtocells have not been widely deployed, it is difficult to evaluate the performance of the proposed scheme with real network or dataset.For this paper,we evaluate the scheme with two simulated networks:one with heterogeneous cells and the other with homogeneous cells.The simulated heterogeneous network contains one macro BS located in the center,two uniformly-distributed femtocells, and a number of uniformly-distributed UEs.The simulated homogeneous network contains 10 femtocells and a number of UEs uniformly-distributed.For both networks,the simulation area is a square region with the side length equaling 25 meters.The bandwidth and the downlink transmission power of the macrocells are 20 MHz and 30 dBm,while those of the femtocells are 6 MHz and 21 dBm, respectively.We assume that the transmission power of UEs is adaptive, i.e., 21 dBm and 30 dBm for the associations with femtocells and macrocells, respectively.The power spectral density of AWGN is set to-174 dBm/Hz.In the simulations,we use the close-in free space reference distance model with frequency-dependent path loss exponent for 5G scenarios to model the wireless channel,given by[32]:

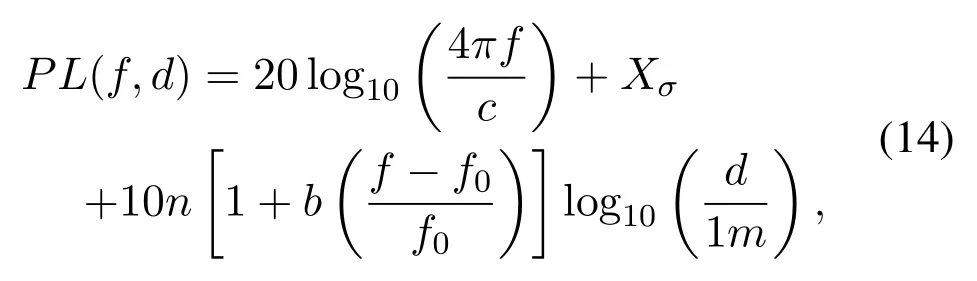
wheref=3.5 GHz is the carrier frequency,n=2.59 is the path loss exponent,b=0.01 is the slope,Xσ=7.4 dBm represents the shadowing, andf0= 39.5 GHz is the reference frequency.Note that, the above model has a quite wide applicability in the frequency bands of 5G and beyond, andbin the middle entry brings in a fine adjustment based on reference frequency and reference distance 1m.

4.1 Experience Pool Demonstration

Representative values forθshould be taken to form an appropriate experience pool,and in the simulations we take values{0.01,0.05,0.1,0.2,0.4,0.6,0.8,1,1.5,2,5,10,20,30,40}so that the variations of the metrics are clearly demonstrated.UE fairness,the worst UE’s capacity, and the system capacity for both heterogeneous and homogeneous network scenarios are shown in Figure 3 and Figure 4,respectively.System capacity is obtained by summing up the capacities of all the UEs, as described by (1) in the system model.The worst UE’s capacity represents the capacity of the UE that achieves the minimum.UE fairness are obtained by calculating the Jain’s fairness index based on all the UEs’capacities.Each point in the figures or each performance metric value in the experience pool for the heterogeneous scenario is averaged on 500 simulation rounds with different deployed locations of femtocells and UEs,while those for the homogeneous scenario is averaged on 50 rounds.The number of UEs for the two scenarios are set to 15 and 80,respectively.

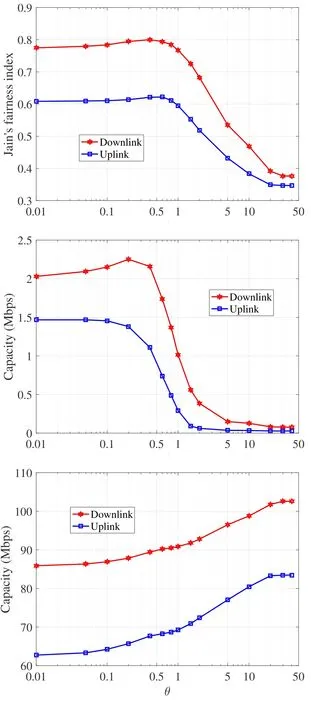
Figure 3.Representative metric values in the experience pool for heterogeneous network scenario.(a)UE fairness;(b)The worst UE’s capacity;(c)System capacity.

For each scenario, both uplink and downlink transmissions are considered and their curves for each metric have similar trends with each other.The major difference between uplink and downlink is the calculation of interferences.Downlink interferences can be calculated directly because the long square utility matrix W contains each possible association for each UE and the downlink interferences from the BSs to each UE are fixed for each of its association possibilities.By contrast, uplink interferences are from the other UEs to the BS associated by the interfered UE.Since UEs locate at different positions,the other UEs’association results affect the calculation of the total interference suffered by this UE.Therefore,W is unable to be obtained before knowing the precise association result.However,this matrix is an input necessity of the designed scheme.To solve this paradox, we consider that each BS is usually associated with the UEs around it, so uplink interferences can be approximately calculated by ignoring the precise locations of the UEs and assuming them colocate with the associated BS.In this way, an approximate capacity matrix is obtained.Since the number of UEs is larger than the number of BSs, UEs have more chance to appear on the border of the simulation region during each deployment.Therefore, downlink interferences to the UEs should be smaller than uplink interferences on average,which makes the uplink curves lower than the downlink ones in the figures.

Whenθis small,the association result is dominated byfij(·).Since the macro BSs have much larger bandwidth and transmission power than femtocells, most UEs prefer the macro BS and averagely share its resource,making quite high fairness and high minimum UE capacity,as shown by Figure 3a and 3b.However,it is disadvantageous for the system capacity shown by Figure 3c because too many UEs share the resource of the macro BS while ignoring the femtocells.Along with the increment ofθ, some UEs gradually change their associations to the femtocells, until all the BSs averagely share all the UEs.In this case, some UEs associating with the femtocells may be relatively far from their BSs and the transmission power of the femtocells is relatively small, so the capacities achieved by these UEs decrease.On the contrary,the UEs still associating with the macrocell obtain more bandwidth than before, which increases their capacities.Therefore,UE fairness of the system is obviously impacted,as shown by the decrease of the Jain’s fairness and the worst UE’s capacity in Figure 3a and 3b,respectively.Seen from Figure 3c,system capacity increases,which is actually benefited from the increase of the capacities of the UEs still associating with the macrocell.

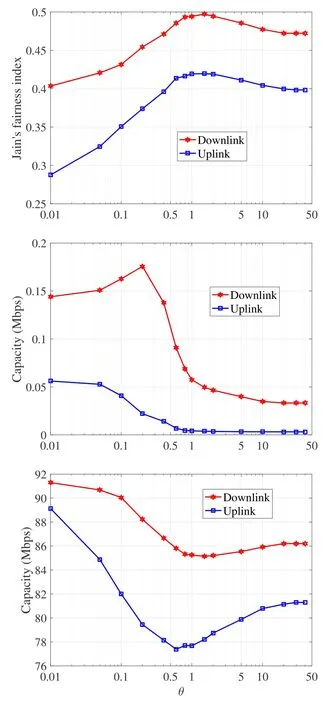
Figure 4.Representative metric values in the experience pool for homogeneous network scenario.(a) UE fairness;(b)The worst UE’s capacity;(c)System capacity.

The homogeneous scenario does not contain a macrocell, so the effects caused by large bandwidth and high transmission power of a macrocell do not appear in Figure 4.Whenθis small, system capacity gradually decreases with the increment ofθdue to the fact that some UEs are gradually pushed to further BSs by the load balancing effect,as shown by the left part of Figure 4c.Meanwhile, these UEs’ capacities increase due to the fact that they get more bandwidth from the further BSs,so UE fairness of the whole system increases, as shown by the left part of Figure 4a.Whenθbecomes relatively large, UEs always associating with previous BSs get more and more released bandwidth from the UEs changing to other BSs,which dominates the variation of the system capacity and makes it slightly increasing,as shown by the right part of Figure 4c.By further increasingθwhen it is already large,the superiority of these UEs becomes more and more obvious, which slightly decreases UE fairness,as shown by the right part of Figure 4a.

4.2 Comparison with Representative Schemes

Seen from the above subsections,downlink and uplink results are not the same but they obviously have similar trends,so it is possible to combine them for association decisions and there would not be much difference by slightly varying the weights between downlink and uplink.Downlink transmissions in a traditional wireless communication system are usually much more than uplink transmissions, but recent and future IoT applications bring in a large amount of uplink flows.Therefore,we set equal weights for downlink and uplink in the simulations of the decision process in this subsections.

Several representative schemes are compared with the proposed scheme in both heterogeneous and homogeneous network scenarios.The compared schemes are an SINR-based scheme in [4], a scheme based on the simulated annealing algorithm inspired by [16], a scheme based on the Q-learning algorithm inspired by[8],and a random association scheme.As an experience obtained from the above subsection,we show in this subsection the curves withθ= 0.3 for our scheme,which achieves a tradeoff between utilityfij(·) and fairness.Meanwhile, we show the curves withθ=0 to indicate the optimality gap between this tradeoff and the case purely maximizing the summation offij(·).Note thatθ= 0 does not correspond to the maximization of the system capacity but that offij(·).This is already explained in the system model and the phenomenon is demonstrated by Figure 3c and 4c,where the point withθ=0 is not the highest.The curves for heterogeneous and homogeneous scenarios in Figure 5 and 6 are obtained by averaging 1000 and 200 rounds of simulations,respectively.

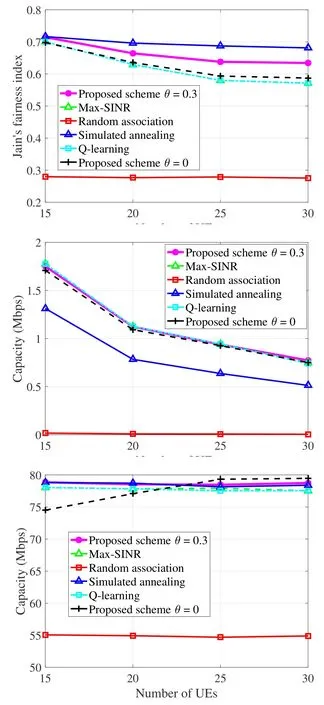
Figure 5.Comparison with representative schemes for heterogeneous network scenario.(a) UE fairness; (b) The worst UE’s capacity;(c)System capacity.

Since the BSs and UEs are both uniformly distributed,interferences for adjacent cells could be similar due to their similar locations, so the SINR-based scheme actually tends to split the UEs to the cells in a relatively averaged way, i.e., the whole region is clearly divided into irregular cells when the number of UEs increases.Therefore, both UE fairness and system capacity features of the SINR-based scheme are usually not bad, and this scheme could be considered as a milestone scheme to compare the other schemes’ performances.The random association scheme chooses a random BS for each UE,so its performance should be undoubtedly the worst in all the compared schemes.The figures could show the gap between this scheme and another scheme(e.g.,the proposed scheme)indicating the gain of a cell association optimization.

Jain’s fairness index, the worst UE’s capacity (i.e.,the max-min fairness), and system capacity for the two scenarios are shown in the subfigures, respectively.Since the proposed scheme withθ= 0.3 reaches a tradeoff between utility and fairness, its Jain’s fairness index value is high.The implemented Q-learning based scheme also applies on our designed long square utility matrix, so its fairness is equally high.The simulated annealing based scheme searches for a quite long time toward the maximization of the total proportional-fair utility, so its Jain’s fairness index value is undoubtedly high.Because of the effect caused by the macrocell,the features in Figure 5 may not be always the same as in Figure 6.For example,max-min fairness of simulated annealing is lower than the others in Figure 5b, but it is higher in Figure 6b.Meanwhile,the figures show that the proposed scheme and the simulated annealing based scheme both outperform the SINR-based scheme and the Q-learning based scheme in terms of Jain’s fairness index.In terms of system capacity,the proposed scheme,the Qlearning based scheme,the simulated annealing based scheme, and the SINR-based scheme are all high, as shown in Figure 5c and 6c.The proposed scheme can reach an even higher system capacity when differentθvalues are taken,but a tradeoff among multiple performance metrics is usually required in a real network.Random association reaches a poor fairness as well as a low system capacity in both scenarios.

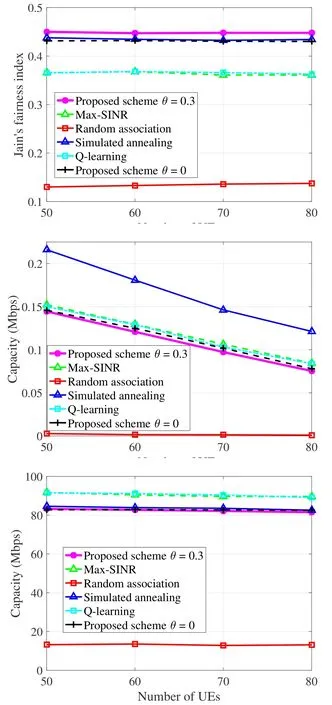
Figure 6.Comparison with representative schemes for homogeneous network scenario.(a) UE fairness; (b) The worst UE’s capacity;(c)System capacity.

In terms of computational time, we feel that Qlearning based scheme and simulated annealing based scheme should be both slow, because they need a large amount of iterations to search for an appropriate association.For the former, the number of iterations is set to 1 million and the simulation may break when no Q value changes 0.01% after 20000 iterations.For the latter, iteration stops when the temperature anneals from 100 to 50 degrees with a rate equaling 0.99995.Settings for evaluating the computational time in Figure 7 are completely the same as Figure 5 and 6, and 100 rounds are taken to smooth the averaged curves.The proposed scheme transforms heuristically the original cell association problem into a 2-dimensional assignment problem.As a common knowledge,such a problem can be solved by the Hungarian algorithm, which represents a type of well-known developing polynomial-time algorithms in mathematics.Withmagents, a muture implementation of this type of algorithms has a complexity ofO(m4), such as the code we used for simulations.Since the matrix on which the algorithm is applied hasM×MNdimensions,the complexity of the proposed scheme isO[(MN)4].Some recent studies in mathematics claimed that an advanced version, called the Kuhn-Munkres algorithm, could achieve a complexity ofO(m3) [33], so the time cost of the proposed scheme may further decrease in the near future.

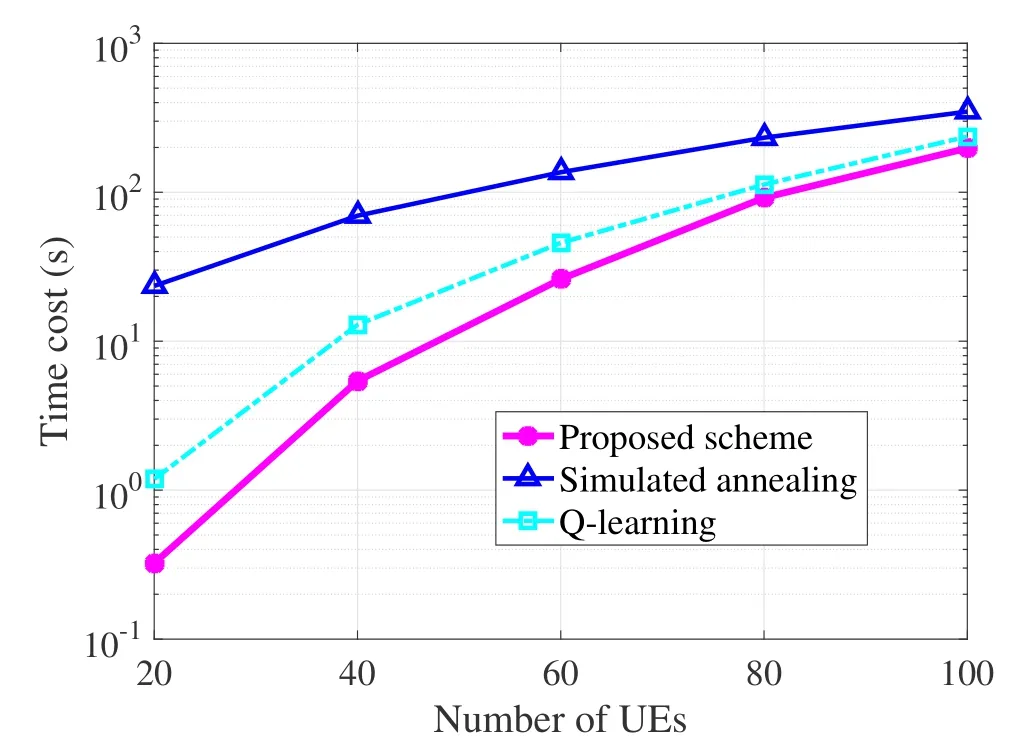
Figure 7.Comparison of time costs.

Transforming a non-polynomial problem heuristically into a polynomial problem has already been a big progress for this research topic.Meanwhile, we also wonder whether the proposed scheme could complete the optimization process with a smaller time cost than Q-learning and simulated annealing,because the difference of their time costs is determined byM,N,and the number of iterations set for these searching schemes.The proposed scheme is significantly faster than the other two schemes, demonstrating our intuition that the two searching schemes need many iterations to find a near-optimal solution.With the increment of the number of UEs,the time costs of the proposed scheme and the Q-learning based scheme both increase fast,because they both apply on theM×MNlong square utility matrix.By contrast, that of the simulated annealing based scheme does not augment so fast, due to the fact that it applies on theM ×Nutility matrix.However, the two searching schemes should keep a large number of iterations, so that a near-optimal solution for the objective utility function could be found.Besides, time costs of max-SINR scheme and random association are extremely low due to the fact that they do not require any iteration, so they cannot be drawn in the figure.As a summary,the proposed scheme guarantees a quite high fairness and a large system capacity within an obviously shorter computational time than the two searching schemes.

V.CONCLUSION

Cell association in future networks became a critical issue and we proposed a polynomial-time scheme for cell association with generic utility functions.By employing the VBS method to transform heuristically the problem into a polynomial-time solvable form,the scheme balanced multiple performance metrics with the usage of a weighting factor taken from the designed experience pool.The pool contained a series of these factor values and corresponding performance metric values obtained by simulations during the experimental process.Performance of the proposed scheme was demonstrated by extensive simulations for uplink, downlink, homogeneous scenario,and heterogeneous scenario.Compared with simulated annealing and Q-learning, the proposed scheme achieved high UE fairness and large system capacity with a relatively low time cost.

ACKNOWLEDGEMENT

This document is the results of the research project funded by the National Natural Science Foundation of China under Grant No.61971176, and in part by the Applied Basic Research Program of Wuhan City under grand 2017010201010117.