Trajectory Design for UAV-Enabled Maritime Secure Communications:A Reinforcement Learning Approach

Jintao Liu,Feng Zeng,Wei Wang,2,*,Zhichao Sheng,Xinchen Wei,Kanapathippillai Cumanan

1 School of Information Science and Technology,Nantong University,Nantong 226019,China

2 Nantong Research Institute for Advanced Communication Technologies,Nantong 226019,China

3 Key Laboratory of Specialty Fiber Optics and Optical Access Networks,Shanghai University,Shanghai 200444,China

4 Department of Electronic Engineering,University of York,York,YO10 5DD,United Kingdom

Abstract: This paper investigates an unmanned aerial vehicle (UAV)-enabled maritime secure communication network, where the UAV aims to provide the communication service to a legitimate mobile vessel in the presence of multiple eavesdroppers.In this maritime communication networks (MCNs), it is challenging for the UAV to determine its trajectory on the ocean,since it cannot land or replenish energy on the sea surface, the trajectory should be pre-designed before the UAV takes off.Furthermore, the take-off location of the UAV and the sea lane of the vessel may be random, which leads to a highly dynamic environment.To address these issues,we propose two reinforcement learning schemes,Q-learning and deep deterministic policy gradient (DDPG) algorithms,to solve the discrete and continuous UAV trajectory design problem, respectively.Simulation results are provided to validate the effectiveness and superior performance of the proposed reinforcement learning schemes versus the existing schemes in the literature.Additionally, the proposed DDPG algorithm converges faster and achieves higher utilities for the UAV,compared to the Q-learning algorithm.

Keywords: maritime communication networks(MCNs); unmanned aerial vehicles(UAV);reinforcement learning; physical layer security; trajectory design

I.INTRODUCTION

With the increase of marine activities,there has been a growing demand for maritime communications[1, 2].In contrast to the communication rate that can be supported by the terrestrial cellular networks at the scale of Gbps, the data rate of the existing maritime communication networks(MCNs)only offers a few Mbps due to the difficulty of building communication facilities on the ocean.Therefore, the maritime communications bring up new challenges, which need to be treated carefully to unlock the potential of the MCNs.

Currently,satellites can provide global communication services to the maritime mobile terminals.However, their transmission rate is usually limited and the communication delay is still large[3, 4].Moreover,high gain antennas are always required for maritime mobile terminals to enjoy the broadband services.As an alternative, the terrestrial cellular networks also can extend the communication services to the ocean by deploying base stations (BSs) along the coast[5].However,their coverage area is usually limited.Furthermore, a vessel-based multi-hop system has been proposed to extend the offshore coverage in the literature[6, 7].However, this system lacks flexibility,since most vessels follow fixed sea lanes.

Different from maritime satellites and terrestrial BSs, unmanned aerial vehicles (UAVs) have shown potential capabilities to support maritime communications[8, 9].However, the open nature of UAV-to-ocean wireless channels makes the information transmission more vulnerable[10, 11].Thus,UAV-enabled MCNs bring up the various physical layer security issues.Recently,different schemes have been proposed for UAV secure communications in the literature, e.g., [12-16].However, the works in [12-16]mainly adopted the conventional optimization approaches, such as successive convex approximation and alternating iterative algorithms,which could only achieve suboptimal or near-optimal results.More importantly, the proposed conventional optimization algorithms are not robust enough to different dynamic environments.Therefore they are unsuitable for practical scenarios in maritime secure communications.This is mainly due to the fact that the UAV cannot land or replenish energy on the sea surface, its trajectory on the ocean should be designed before the UAVs are deployed to accomplish their tasks.Furthermore, the take-off location of the UAV and the sea lane of the vessel may be random,which leads to a highly changing environment.Therefore,designing UAV trajectory in the dynamic environment is of paramount importance for maritime secure communications.

To address the above mentioned issues, reinforcement learning schemes have been proposed for designing UAV trajectory in dynamic environments in the literature.In [17], the authors studied the sum rate maximization problem for a UAV-aided multiple-users network, where the UAV trajectory was optimized by using Q-learning algorithm without any explicit environment information.In [18], a deep reinforcement learning algorithm was proposed for UAV trajectory design by jointly considering coverage and fairness.A UAV-assisted communication system was considered in[19],in which the decentralized UAV trajectory was designed based on an enhanced Q-learning algorithm.Moreover,a sum rate maximization problem for UAVaided cellular network was studied in [20], in which a reinforcement learning algorithm was developed to optimize the UAV trajectory.However, the works in [17-20] assumed that the ground users are static.To address this issue, a UAV-assisted downlink transmission network with mobile users was considered in[21],where Q-learning was proposed to choose the deployment location.Furthermore,in[22],a deep deterministic policy gradient(DDPG)-based reinforcement learning algorithm was proposed to optimize UAV 3D trajectory and mobile users frequency band.Recently,in[23],a multi-agent deep reinforcement learning approach was extended to UAV secure communication networks.However, the aforementioned works, e.g.,[17-23], only focused on the terrestrial cases, which may not be applicable to UAV-aided maritime communication scenarios.This is due to the fact that the vessels on the ocean,unlike the users in the terrestrial case with random distributions and moving patterns,often follow a set of predefined sea lanes for safety,and they have predictable mobility patterns.Moreover,in contrast to the channel state information(CSI)estimation in the terrestrial case,the CSI acquisition in the maritime scenario is more challenging due to the harsh propagation environments[9].Thus,to improve the security performance,the practical vessel mobility and maritime environment effects need to be considered in UAV trajectory design.

Motivated by the above aspects, we investigate a UAV-enabled MCNs in this paper, where the UAV aims to provide the communication services to the legitimate mobile vessel in the presence of multiple eavesdroppers.Furthermore, we consider a practical UAV-ocean channel model that includes both largescale and small-scale fading components.Since it is impossible to acquire the random small-scale fading before the UAV takes off, we assume that only the large-scale fading components are available in advance.Moreover, we further assume that the UAV’s take-off locations on the coast are not fixed and the sea lane of the mobile vessel is random.Considering these facts, we propose two Q-learning and DDPGbased reinforcement learning algorithms to optimize the maritime UAV trajectory.To the best of the authors’ knowledge, reinforcement learning-based trajectory design for UAV-enabled MCNs has not been reported in the literature, and the main contributions are summarized as follows:

· We consider a more practical UAV-ocean channel model and formulate the trajectory design problem of UAV-enabled maritime secure communication networks.

· Then, we develop Q-learning and DDPG-based reinforcement learning algorithms for the trajectory design of the maritime UAV.The proposed algorithms take into account the UAV’s initial locations and vessel’s sea lanes,and hence they are robust enough to adapt according to the highly dynamic environments.

· Finally,simulation results are provided to demonstrate the superior performance of the proposed reinforcement learning schemes against the existing approaches in the literature.

The rest of the paper is organized as follows.In Section II, the system model and the problem formulation are introduced.Two reinforcement learning algorithms are developed in Section III.In Section IV,simulation results are presented.Finally, Section V concludes the paper.

II.SYSTEM MODEL AND PROBLEM FORMULATION

We consider a UAV-enabled MCNs as shown in Figure 1, where the UAVSaims to provide the communication service to a legitimate mobile shipDin the presence of multiple eavesdroppers{E1,E2,··· ,Ek}.Here, the UAV is connected to terrestrial BSs or maritime satellites to receive data and instructions[8, 9].More specifically, when a mobile shipDneeds the communication service at some time, the control center chooses one idle UAVSalong with the optimized trajectory to serveDin the presence of{E1,E2,··· ,Ek}.After completing the requested communication service or reaching the maximum flight time, the UAV will return back to the charging station at the coast.We consider a particular UAV flight timeT, which is divided intoNtime slots withdt=T/N, whereN≜{1,··· ,N}.Furthermore, a 3D Cartesian coordinate system is considered, where the coordinate of the mobile ship can be denoted as(xd[n],yd[n],0).The coordinates(xek[n],yek[n],0)represent the location of thek-th eavesdropper.Moreover, we assume that UAV has a fixed flight heightH[8, 9, 12-14],i.e., (xs[n],ys[n],H).Additionally, the coordinates(x0,y0) and (xF,yF) represent the initial and final horizontal positions of the UAV, respectively.Under the above setting,the mobility constraints of the UAV can be formulated as

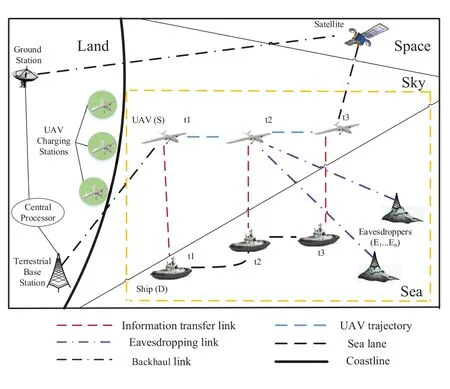
Figure 1.Illustration of a UAV-enabled MCNs: a secure communication example.

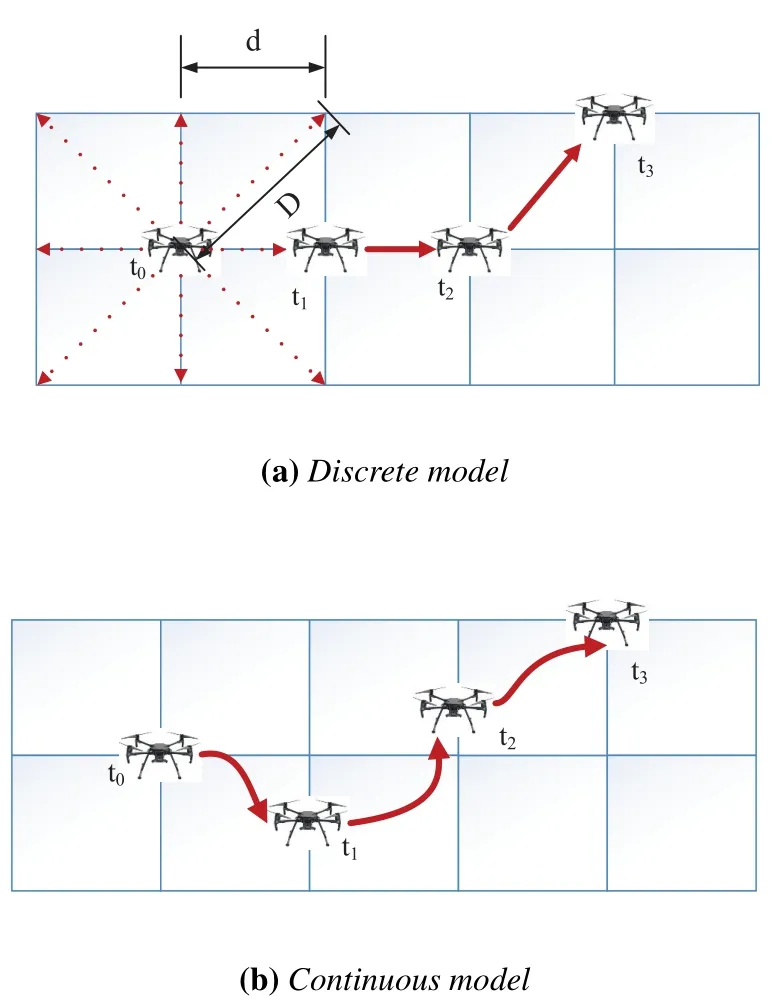
Figure 2.UAV trajectory design model.

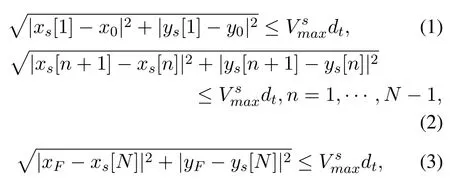
whererepresents UAV’s maximum speed.Furthermore, as most vessels follow fixed sea lanes in practice[8,9],we assume that the ship has a fixed trajectory constraints

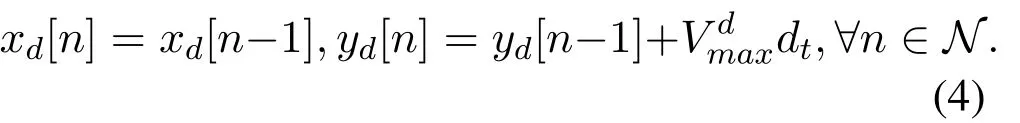
wheredenotes the mobile ship’s maximum speed.

Besides, we adopt a more practical UAV-ocean channel model[8,9],which can be defined by

where{gsd[n],gsek[n]}andrepresent the large-scale and small-scale fading coefficients,respectively.The symbolβ0represents the reference power gain, anddsd[n] anddsek[n] denote the distances between UAV-to-Dand UAV-to-Ek,respectively.The coefficients{gsd,gsek} ∈CN(0,1) andK[n] represents the Rician factor.In practice, the vessels on the ocean often follow a set of predefined sea lanes and then the historical data can be obtained from the AIS.Thus,it is assumed that the coefficients{gsd[n],gsek[n]}andK[n] are available, whereas the coefficients{gsd,gsek}are unknown[8, 9].Based on the above setting,the signal-to-interference plus-noise ratio(SINR)and the average rate ofDcan be derived respectively as

wherePs[n] represents UAV’s transmit power, E(·)denotes the expectation, andrepresents the noise variance.At the same time,the SINR and the average rate atEkcan be defined respectively as

wheredenotes the noise at thek-th eavesdropper.

Our aim is to optimize the UAV’s trajectory to maximize the secrecy rate from the UAV to the ship, and thus,the optimization problem can be expressed as

Since the problem defined in(9)needs to deal with the dynamic movement of both the UAV and the vessel,it is challenging to solve with traditional optimization methods.Furthermore, the initial location (x0,y0) of the UAV and the sea lane (xd[n],yd[n]) of the vessel may be random in practice,which make the optimization problem more intractable.To deal with these issues,a reinforcement learning scheme,which empowers the UAV to making decisions by instantly learning the environment, is developed to address the formulated trajectory design problem.

III.PROPOSED REINFORCEMENT LEARNING ALGORITHMS

We first establish the model to describe the UAV trajectory design problem as shown in Figure 2, which consists of one discrete model and one continuous model.Then, we analyze both the discrete and continuous trajectory design problems in Q-learning and DDPG based reinforcement learning frameworks, respectively.Finally, two reinforcement learning algorithms are proposed to efficiently address the maritime UAV’s trajectory design problem.

3.1 UAV Trajectory Design Model

In Figure 2(a),we first consider a discrete UAV trajectory model,in which the 2D plane is discretized into a finite setS={s1,s2,...}.To determine the trajectory,the UAV first locates at thesnat the beginning of then-th time slot.Once the UAV chose the next discrete point, it will fly to the selected point within then-th time slot.Furthermore, the distance between two adjacent discrete points is set to be asd, and thus, the UAV can reach the maximum distance in a time slot isAs a result, there are altogether nine available spatial points that can be chose by the UAV in each time slot,as shown the square in Figure 2(a).

Different from the discrete model in Figure 2(a),a continuous UAV trajectory model is considered in Figure 2 (b).Since the UAV can move arbitrarily in the continuous trajectory model without being constrained by the top of the square, there are more available actions that can be selected by the UAV in each time slot.Moreover, since the speeds of the UAV and the ship may be different in practice, the proposed continuous trajectory model can enable the UAV to closely follow the mobile ship.

3.2 Q-Learning Framework

To begin with, the Q-learning framework can be represented by a Markov decision process[17-23], i.e.,＜S,A,R,P,γ ＞.

·S={s1,s2,...}is the finite state set of the UAV’s locations at the time slotn, wheresn={xs[n],ys[n],H}.

·Ais the corresponding finite set of actions available to the UAV, as mentioned in Figure 2 (a),there are nine movements in Q-learning framework.

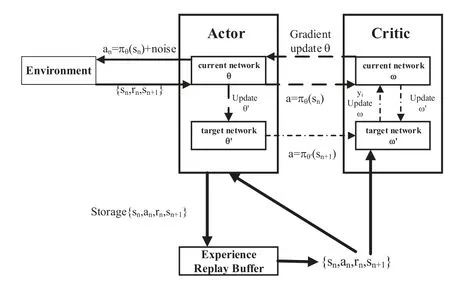
Figure 3.Flowchart of model training in DDPG algorithm.

·Rrepresents the reward function for the UAV,in this paper, which is defined byrn=rs+rb+rf, wherersrepresents the secrecy rate reward,rbdenotes the UAV’s flight boundary penalty,andrfrepresents the flight time penalty.

·Pdenotes the state transition probability.

·γrepresents the discount factor.

In the Q-learning framework, the UAV selects actions based on the following policy in each state,

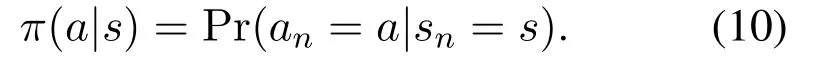
The essence of this framework is to determine the Qvalue,i.e.,

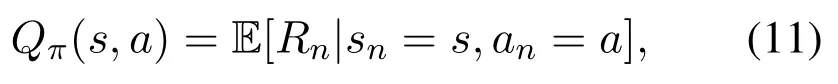
whereQπ(s,a)represents the expectation of the future reward.The symbolRndenotes the total discounted reward at current time slotn,which can be defined as

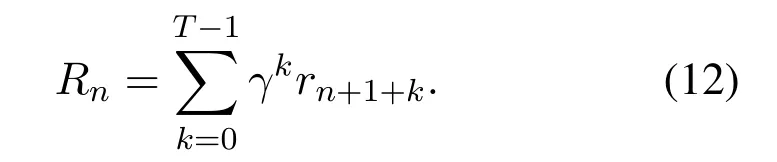
Algorithm 1.Q-learning algorithm for UAV trajectory design.1: Initialize ϵ,α,Qn(sn,an),π(sn);2: for each episode do 3: Initialize the UAV’s positions and speed;4: for each time slot n do 5: Choose action an from the policy πn(sn)with the probability of 1 - ϵ, while randomly choose an available action for exploration with probability of ϵ;6: Perform the action an at the n-th time slot;7: Obtain the new state s′and the reward rn;8: Update the Q-value based on(14);9: Update the state sn =sn+1;10: Update the exploration ratio ϵ=κϵ;11: end for 12: end for

Our aim is to determine an optimal policy to maximize the reward that defined in terms ofrn, which is defined as:

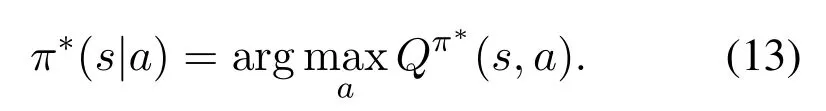
Based on (11) and (12), we can update the Q-table in each step by the following rule:

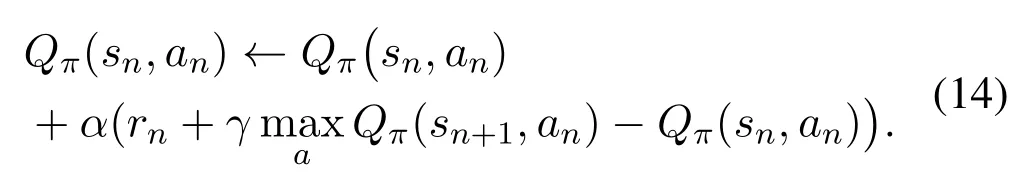
whereα ∈[0,1] represents the step-size parameter.Under the above setting, the proposed Q-learning algorithm can be summarized in Algorithm 1.At the start of each episode, the initial and final positions as well as the initial speed of the UAV are initialized.Furthermore, the vessels follow fixed sea lanes and their positions changing over time.At the time slotn-th, the UAV chooses an actionanaccording to the exploration rateϵ.If the action causes the violations of the flight boundary and time limits, the UAV will receive the individual penaltyrbandrf,whererbandrfare two negative constants.Then the UAV reaches the new states′and obtains the rewardrn.Finally,the Q-values are updated according to the rule defined in(14)(line 8)in Algorithm 1.The total computational complexity of the proposed Q-learning algorithm in Algorithm 1 isO(NNite), whereNandNitedenote the numbers of the time slots and required iterations,respectively.

3.3 DDPG Framework

Compared to the Q-learning algorithm, DDPG is a deep reinforcement learning algorithm,which can address the continuous and high-dimensional spaces[22].Therefore, we adopt the DDPG framework to deal with the UAV’s continuous trajectory design problem in Figure 2(b).The flowchart of model training in the DDPG algorithm is provided in Figure 3.

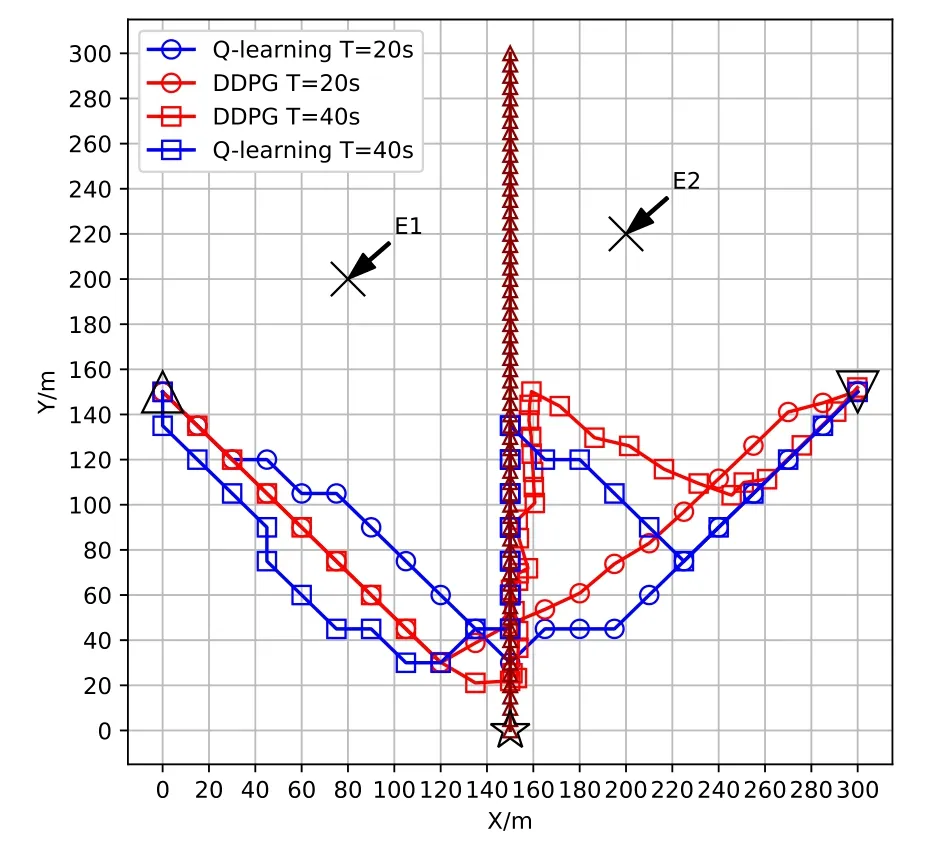
Figure 4.Optimized UAV trajectories during different time durations T.

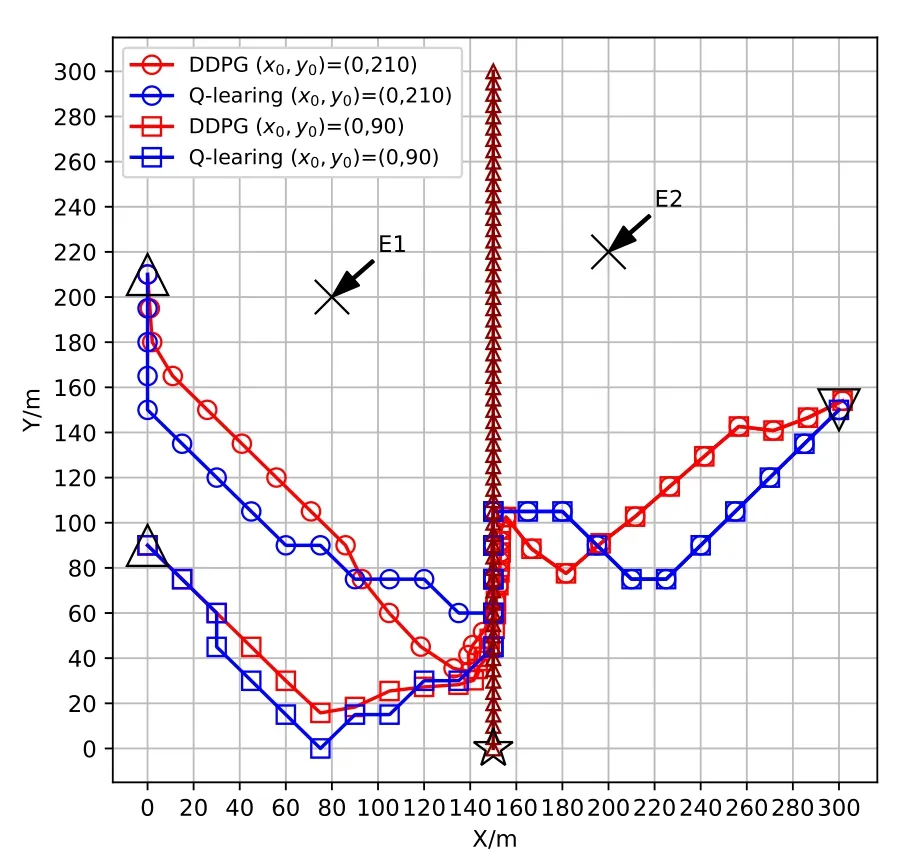
Figure 5.Optimized UAV trajectories with different initial positions(x0,y0).

· Actor neural network (current network): It is responsible for updatingθ, and selectingaaccording tos;

· Actor neural network (target network): It is responsible for copyingθtoθ′, and selectinga′based ons′;

· Critic neural network (current network): It is responsible for calculatingQ(s,a,ω)and updatingωaccording toyn=r+γQ′(s′,a′,ω′), wherer=rs+rb+rf;

· Critic neural network (target network): It is responsible for copyingωtoω′, and calculatingQ′(s′,a′,ω′).

In this paper, the DDPG algorithm adopts the soft target update policy,which can be defined as

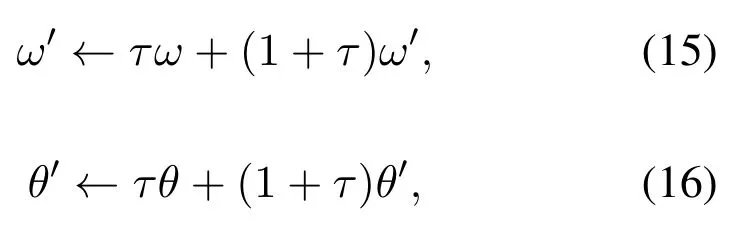
Algorithm 2.DDPG algorithm for UAV trajectory design.1: Initialize π(s|θ)and Q(s,a|ω)with θ and ω;2: Initialize θ′=θ and ω′=ω;3: Initialize Rb;4: for each episode do 5: Initialize UAV’s locations and speed;6: Initialize a Gaussian noise nN and an observation state s0;7: for each time slot n do 8: Select the action an based on(17);9: Update sn+1 and rn by taking the action an;10: Store(sn,an,rn,sn+1)into Rb;11: Sample a random minibatch of Nb;12: Set yn =rn+γQ′(sn+1,π(sn+1|θ′)|ω′);13: Update the critic network based on(18);14: Update the actor network according to(19);15: Update the target networks based on(15)and(16).16: end for 17: end for

whereτ ≪1 denotes the updating factor.Moreover,we can further improve the exploration efficiency by adding random noise as follows:

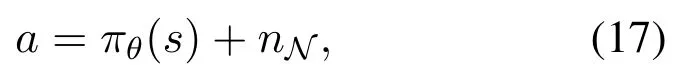
wherenN ～CN(0,σ2N).Therefore, the parameters can be updated based on the loss function:

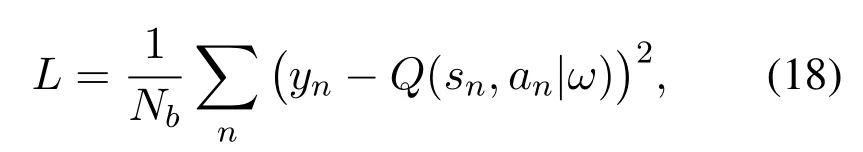
whereNbis the batch size andyn=r+γQ′(s′,a′,ω′).In addition, the actor network can be updated by the following policy:

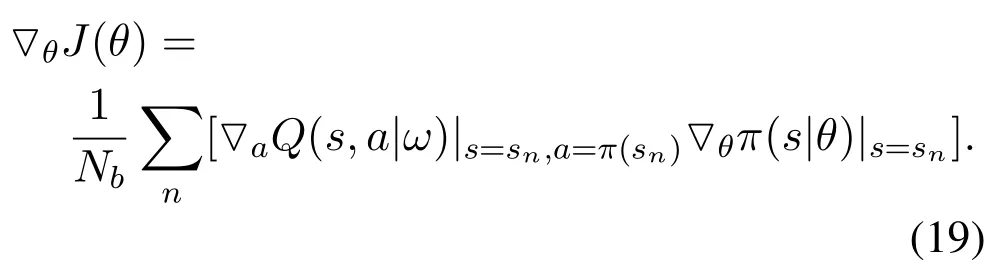
Based on these settings, the proposed DDPG algorithm is presented in Algorithm 2.At the beginning of each episode, the UAV’s initial position is randomly selected on the coast, and the final position and the starting speed are initialized.The vessels follow a set of fixed sea lanes on the ocean.At the time slotnth, the UAV chooses actionanaccording to the policy (17).If the action causes the violations of the UAV’s flight boundary and time limits, the UAV will obtains the corresponding penaltyrbandrf.Then the UAV can achieve the newsn+1andrn,and stores(sn,an,rn,sn+1) in the bufferRb.Next, we update the critic and actor networks based on the loss function (18) and policy gradient (19), respectively.Finally,the target networks updatesω′andθ′slowly according to(15)and(16)as shown in line 15 in Algorithm 2.The total complexity of the proposed DDPG approach in Algorithm 2 iswhereni,i ∈{j,l},denotes the number of neurons inithlayer,JandLrepresent the connected layers of actor and critic network,respectively.

IV.SIMULATION RESULTS

The setting of simulation is described in the following.The initial horizontal location(x0,y0)of the UAV is randomly selected between the interval(0,[0,300])m, and the final horizontal coordinate is (xF,yF) =(300,150) m.The initial horizontal coordinate of the mobile ship and two eavesdroppers are set to be (xd[n],yd[n]) = (0,150) m, (xe1[n],ye1[n]) =(80,200)m and (xe2[n],ye2[n]) = (200,220) m, respectively.Moreover, the channel power gainβ0and the Rician factorK[n] are assumed to be 40 dBm and 31.3, respectively[8, 12].Furthermore, unless otherwise specified, we setσ2d=σ2e=-30 dBm,Ps[n] = 15 dBm,m/s[8, 9], andH= 50 m[12-14], respectively.Besides, the parameter settings of Q-learning are shown as below.The learning rate isα= 0.3, the discount factor isγ= 0.99, the initialized exploration ratio isϵ= 1 and the decay factor isκ= 0.99995[17].Furthermore, in DDPG algorithms, the replay buffer capacity and the batch size are set to beRb= 100000 andNb=64,respectively[20].

Figure 4 shows the trajectories of the UAV determined by Q-learning and DDPG algorithms during different timeT, respectively.The symbols⋆and△represent the initial locations of the mobile ship and the UAV, respectively, and▽denotes the final position of the UAV.From Figure 4, whenT= 20 s, the UAV almost directly flies to the final position in both Q-learning and DDPG algorithms.However,whenTis large enough, i.e.,T= 40 s, the UAV is able to avoid the eavesdroppers while following the mobile ship as long as possible.Furthermore, compared to the Q-learning scheme,the proposed DDPG approach can enable the UAV to more closely follow the mobile ship since the UAV can move arbitrarily in the continuous space without being constrained by the top of the square.

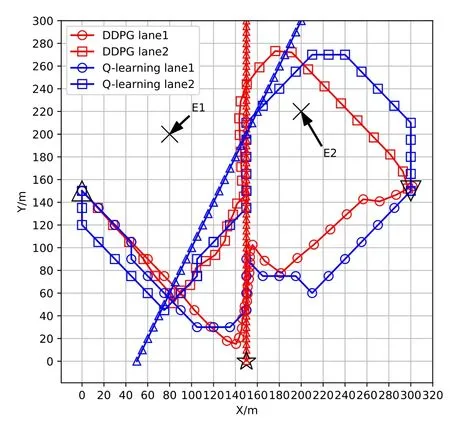
Figure 6.Optimized UAV trajectories with different vessel’s sea lanes(xd[n],yd[n]).

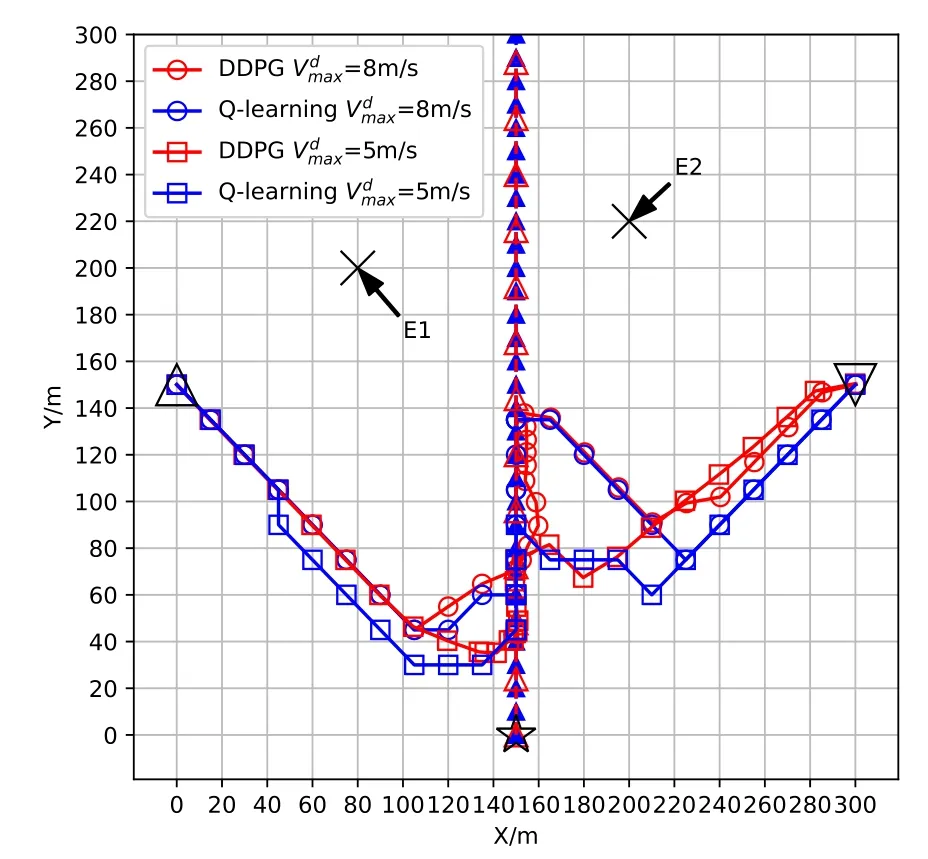
Figure 7.Optimized UAV trajectories with different vessel’s speed .

Figure 5 depicts the trajectories of the UAV obtained from Q-learning and DDPG algorithms versus different initial positions (x0,y0) withT= 35 s, respectively.Since the take-off location of the UAV may be random distribution on the coast, the conventional optimization approaches cannot deal with the dynamic environment issue.In our proposed reinforcement learning frameworks, both the Q-learning and DDPG algorithms take into account the UAV’s initial locations,and hence can solve the dynamic trajectory planning problem.As can be seen in Figure 5,for any given UAV’s initial positions (x0,y0) = (0,210)s and (x0,y0) = (0,90) s, the proposed Q-learning and DDPG algorithms yield similar aerial trajectories which are similar to the ones depicted in Figure 4.Furthermore,when the UAV flies to the final position from the mobile ship,the Q-learning and DDPG algorithms yield the same trajectories for different initial positions.The reason is that the UAV can always use the minimum available flight time to reach the final location for the same Q-learning or DDPG algorithm.

Next, we present the UAV’s trajectories that obtained from the Q-learning and DDPG algorithms versus different vessel’s sea lanes(xd[n],yd[n])withT=35 s.The vessels lanes can be obtained from the shipborne AIS in practice, which facilitates the efficient scheduling of UAVs on the ocean.As shown in Figure 6,for given vessel’s sea lane 1(red△,= 5 m/s) and lane 2 (blue△,both the proposed Q-learning and DDPG algorithms yield trajectories to steer away from the multiple eavesdroppers while following the mobile ship as long as possible.In addition,compared to the UAV in the sea lane 1,the UAV in sea lane 2 cruises at the center location of the eavesdroppers instead of following the mobile vessel all the time.The reason is that the UAV flies to the possible center location to avoid eavesdropping.

Figure 7 illustrates the UAV’s trajectories obtained by both the Q-learning and DDPG algorithms versus different vessel’s speedswithT= 30 s.From Figure 7, whenis small, i.e.,= 5 m/s,the UAV almost directly flies to the mobile vessel.This implies that the UAV can follow the mobile vessel more quickly.However,when vessel’s speedis large, i.e.,= 8 m/s, the UAV can follow the mobile ship with a longer time.The reason behind this behavior is that when the vessel’s speedis large,a less waiting time needs to be allocated for the UAV.

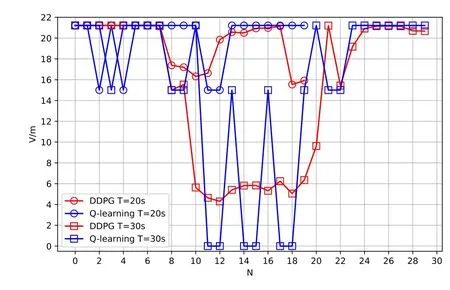
Figure 8.Flight velocity of the UAV with different time durations.

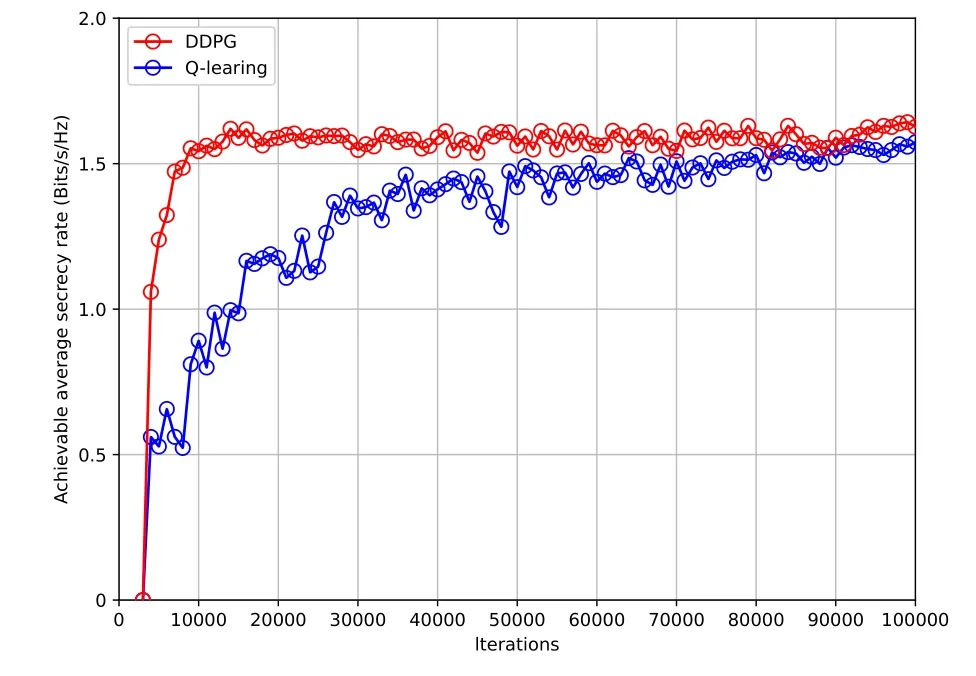
Figure 9.Average rewards of the UAV versus episodes under different algorithms.

Figure 8 presents the UAV’s horizontal velocity of the Q-learning and DDPG algorithms versus differentN.From Figure 8, whenT= 20 s, the UAV flies to the final position almost with the maximum velocityin both the proposed Q-learning and DDPG algorithms.However,asTincreases,(e.g.,T= 30 s), the UAV based on the DDPG algorithm will reduces the horizontal velocity to 5 m/s to follow the vessel (= 5 m/s) as long as possible.As in DDPG algorithm,similar horizontal velocity of the UAV can be observed in the Q-learning algorithm.Nevertheless, different to the DDPG algorithm that can flexibly adjust UAV’s speed to follow the mobile vessel, the UAV in Q-learning algorithm reduces the horizontal velocity to 0 at a certain period of time before reaching the final position.This is because that the UAV needs to hover at those positions for waiting the mobile ship.

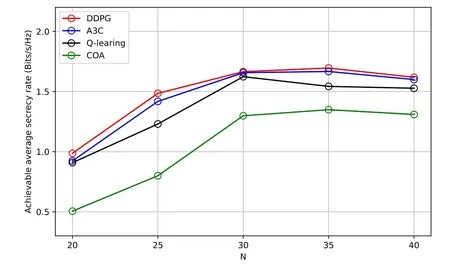
Figure 10.Performance comparison under different algorithms versus N.

Figure 9 shows the average reward received by the UAV in the proposed Q-learning and DDPG algorithms withN= 30.From Figure 9, the achievable rewards of both algorithms first increase and gradually stabilize with the number of iterations.Furthermore,it can be observed that the proposed DDPG algorithm converges faster than the Q-Learning algorithm, due to the reduction in the size of the available action set and the improvement in the efficiency of training data.Moreover, the proposed DDPG algorithm converges to higher average secrecy rate rewards than that of the Q-learning algorithm.This performance observation is due to the reason that the UAV in the considered DDPG algorithm can flexibly select the available actions, which enables the UAV to closely follow the mobile ship.

Finally, we compare the performance of the proposed reinforcement learning algorithms (DDPG and Q-learning) with the A3C and conventional optimization algorithms (denoted as COA) with different UAV’s flight time slotsN.As can be seen in Figure 10,the DDPG and A3C algorithms have similar performances in each setting.This is due to the fact that they all have an actor-critic framework.Furthermore,compared to the Q-learning scheme, the proposed DDPG scheme achieves a better secrecy rate performance.This is because that the proposed DDPG approach can flexibly adjust UAV’s speed to match the vessel speed.Besides,the proposed reinforcement learning schemes based on DDPG and Q-learning significantly improve the secrecy rate compared with the COA scheme.The reason is that they can better adapt to the highly dynamic maritime environments.

V.CONCLUSION

This paper studied the trajectory design problem for UAV-assisted maritime secure communications.In particular, two reinforcement learning schemes based on Q-learning and DDPG have been proposed to solve the discrete and continuous maritime UAV trajectory design problems, respectively.The simulation results have validated that the proposed reinforcement learning schemes can obtain a superior performance compared to the existing approaches.Besides, the results have also confirmed that the proposed DDPG scheme converges faster and achieves higher utilities compared to the Q-learning algorithm.Our future work will consider the 3D trajectory optimization of multiple maritime UAVs to offer better communication services for the mobile vessels.

ACKNOWLEDGEMENT

This work was supported by the Six Categories Talent Peak of Jiangsu Province (No.KTHY-039),the Future Network Scientific Research Fund Project(No.FNSRFP-2021-YB-42), the Science and Technology Program of Nantong(No.JC2021016)and the Key Research and Development Program of Jiangsu Province of China(No.BE2021013-1).