Collaborative D2D Communication in Relay Networks with Energy Harvesting

Qiang Li,Pinyi Ren

1 School of Information and Communication Engineering,Xi’an Jiaotong University,Xi’an 710049,China

2 Shaanxi Smart Networks and Ubiquitous Access Research Center,Xi’an 710049,China

Abstract: Although the collaborative transmission of cellular network and device-to-device(D2D)pairs can improve spectrum utilization,it also results in the matual interference, which may be fatal for low-energy D2D pairs.Based on this, we propose in this paper a collaborative D2D transmission scheme with erergy harvesting (CDTEH) in a relay network, where D2D pairs are allowed to access the spectrum of relay network to accomplish their own transmission.In particular, the relay with energy harvesting is arranged to not only expand cellular transmission range but also assist D2D and cellular users to eliminate the mutual interference.To evaluate the performance,rate-energy(R-E) region is introduced.Based on the model, a data rate maximization problem of D2D pair is formulated,subject to a transmission demand of the cellular user and the optimal solution is acquired.Finally,numerical results are provided to validate the proposed scheme improves the data rate of D2D pair ensuring the cellular transmission requirement.

Keywords:energy harvesting;transmission rate;R-E region;collaborative D2D communication

I.INTRODUCTION

In the 5G beyond era, thousands of wireless devices are connected to the communication network, which poses a tremendous challenge to communication resources, particularly spectrum [1].Improving the spectral utilization becomes an urgent problem[2].To tackle the issue, some promising technologies have been put forward, such as non-orthogonal multiple access [3], millimeter wave communication [4], fullduplex technology [5] and so on.In addition to these technologies, the integration of the existing approaches is also a way to deal with the issue.

Device-to-device (D2D) transmission is an important communication paradigm in the future network,which allows two users to directly exchange information without the base station (BS) for scheduling [6].If the dedicated spectrum is allocated to D2D users,it will result in a huge waste of spctrum and slow down the spectral efficiency [7].Allowing D2D pairs to access the spectrum of the cellular networks to communicate can overcome the above problem well [8],which also corresponds to the integration of cellular and D2D technologies.In[9],the authors proposed a D2D power control scheme in the uplink cellular network to achieve coexistence.

Due to the fading caused by the long distance transmission [10], it may be difficult to recovery the signals.To expand communication range, a relay can be placed between users.In [11], the authors put forward a two-way relay protocol to assist the information transfer.In [12], the relay was applied into vehicle-to-vehicle system to improve user experience.As facilitators, the relays may be not willing to relay the messages using their own energy, without receiving benefits[13].Energy harvesting(EH)technology can recharge the battery using the receiving signals.Therefore, applying the EH into relay networks is a promising solution.In [14], the system performance of the energy havesting relay network was analyzed.In[15],the authors proposed a secure relaying scheme in an EH relay network.

Although the integration of cellular and D2D technologies, it also brings an unavoidable problem, in which cellular and D2D transmissions can interfere with each other[16].This may be acceptable to cellular users with basic long-term transmission needs,but it is fatal to D2D users aiming at accomplishing the communications quickly[17].To deal with the issue,some researches have been done.In[18],the authors uesd the pre-coding approach to mitigate the interference.In[19],a interference minimization scheme was proposed,which improved the sum rate of the system.In [20], the authors put forward a channel information sharing strategy to calcellation the interference.Nevertheless,there are two issues that have been overlooked.These methods solved cellular or D2D interference,but the simultaneous removal of mutual interference between cellular and D2D users had not been involved.In addition, the introduced precoding strategy increases the complexity of information processing.

To remedy the gaps,we in this paper propose a collaborative D2D transmission scheme with energy harvesting(CDTEH)in a relay network.Where a relay is placed between cellular user and the BS, while D2D pair can occupy the cellular spectrum to transfer their own information.To relay the signals, the relay can capture energy from the received signals.As such,the relay forwards not only the cellular signal but also D2D signal.Based on this,D2D and cellular receivers can eliminate the matual interference,which has been not studied.The proposed scheme supports the coexistence of D2D and cellular users in relay networks well,which greatly improves the spectrum utilization.The main contribution of this paper can be summarized as follows.Firstly, a collaborative D2D transmission scheme is proposed in a relay network with energy harvesting,which helps cellular and D2D users to remove the matual interference.Secondly, R-E region is introduce to evaluate the system performance,in which we can find the most optimal working status of the network.Thirdly,a D2D rate maximization problem is formulated, guaranteeing the transmission need of cellular user, and the optimal solution is acquired.Finally,simulation results validate the superiority of the proposed scheme.

II.THE SYSTEM MODEL

We consider,as shown in Figure 1,a cellular network,where a pair of D2D users share the uplink channel of the cellular network with a cellular user C.The D2D pair is composed of a transmitter A and a receiver B.Due to obstacles and fading, cellular user C cann not communicate with the base station S directly.Therefore,a relay node R with energy harvesting is arranged between C and S to assist cellular user C to complete the transmission.In particular, R can capture energy from the surrounding environment and use it for its own transmission.As such, R can forward not only the cellular information of C, but also the D2D signal transmitted by A.We assume that all nodes with a single antenna are in half-duplex(HD)mode and concious of CSI in line with the channel estimation.

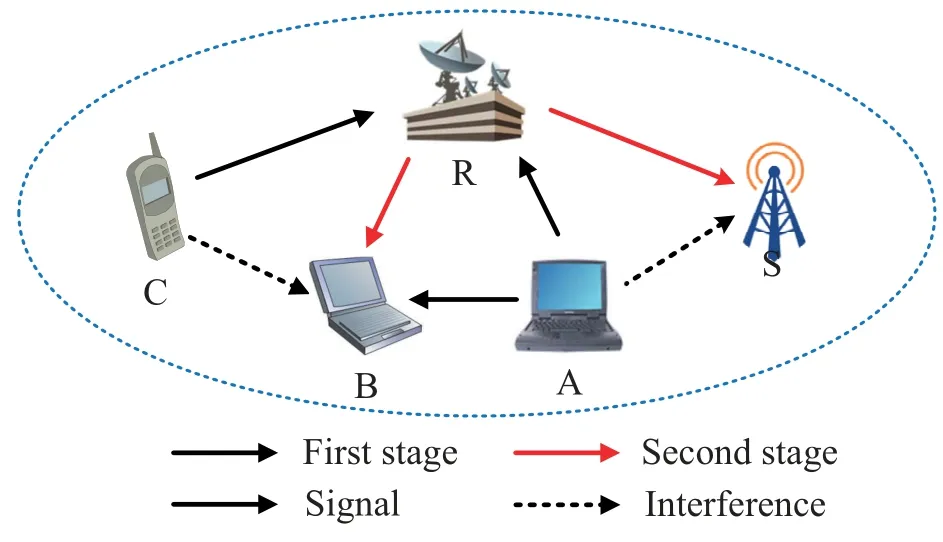
Figure 1.The system model diagram of our proposed scheme.

In particular, R utilizes the amplify-and-forword(AF)protocol to transmit incoming signals from C and A.Assuming that the D2D transmisssion is synchronized with the cellular transmission.Generally, the whole transmission process is divided into two stages.In the first phase,C and A transmit the signalsxCandxAto R and B,respectively.As a result, R and B receive the interference signals from C and A, respectively,while S will receive signal from A.Without loss of generality, the channel gains of the links between C and R, between A and B, between A and R, between B and C, and between A and S are expressed ash1,h2,h3,h4,h5, respectively.After receiving the signals, R harvests energy from them to forward messages, by the way of the energy splitting method(ESM).In the second stage,R transfers the remaining signals to S and B,and the channel gains of the links between R and S and between B and R are denoted byh6andh7,respectively.Combining the two stages,the interference of C to B can be removed using the information forwarded by R.Assuming all channels undergo the quasi-static Rayleigh fading.Therefore,we havehi ～CN(0,Ω|hi|2),fori= 1,2,3,4,5,6,7 for all channels.The distance between nodes corresponding to each channel isdi,i= 1,2,3,4,5,6,7,respectively.

III.COLLABORATIVE D2D TRANSMISSSION WITH ENERGY HARVESTING

As shown in Figure 1, the collaborative D2D transmission scheme with energy harvesting (CDTEH) is divided into two stages.In the first stage, C and A respectively emit the signals.As a result, the signals received at R and B can be expressed as

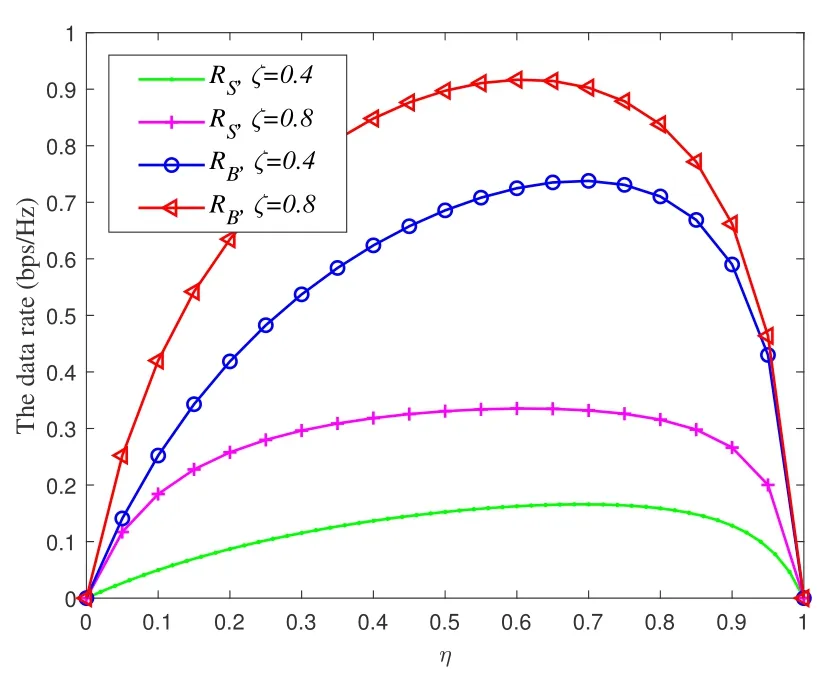
Figure 2.The relationship between the rate and energy splitting ratio η.

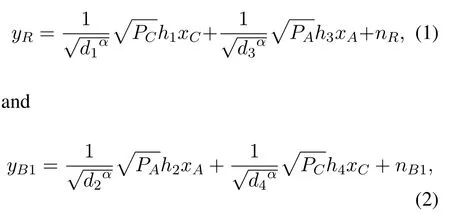
respectively.Here,xCandxAare two unit-power signals intended for S and B, respectively.nR ～CN(0,σ12) andnB1～CN(0,σ22) are the additive white Gaussian noise (AWGN) at R and B, respectively.Andαis the path loss coefficient.

In the light of the ESM,R divides the received signals into two parts,part for the energy harvesting and part for the information transfer.The observation for energy harvesting of R can be given by

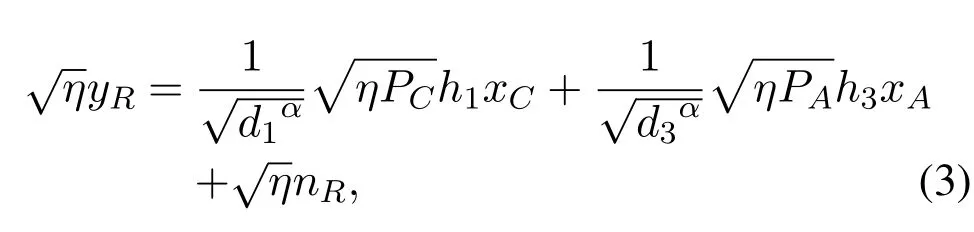
where 0＜η ＜1 represents the energy splitting ratio (ESR) at R.It is noted that R will utilize the captured energy to forward the remaining signals.Consequently,the observation of energy harvesting at R can be computed as

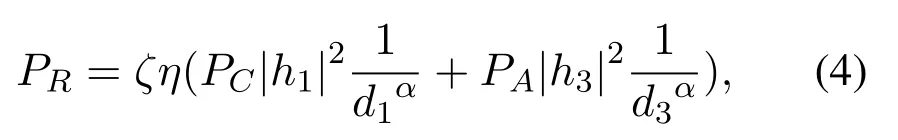
where 0＜ζ ＜1 is the energy conversion efficiency(ECE)at R.

In the second stage, R forwards the remainingwith the AF protocol.As such,S and B will simultaneously receive the signal from R.The signal forwarded by R can be given as follows.

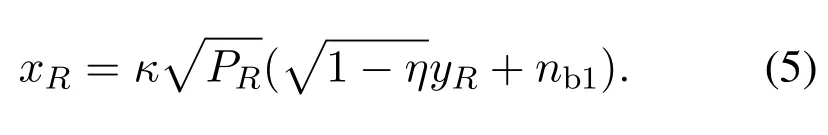
Here,nb1～CN(0,σb12)is the AWGN produced by the signal processing at R.The energy normalization coefficientκof R can be calculated by

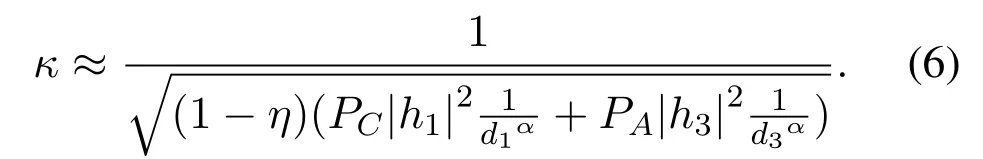
Whereσ12andσb12can be neglected compared with the energy delivered by R.

Through the two stages,S receives the signals from R and A.Because the system works in the HF mode,S can recovery its own signal using the maximum ratio combining.The information processing during the first stage is invalid for S,since it does not involve S’s target signal transmission.As such,the received signal at S can be derived as

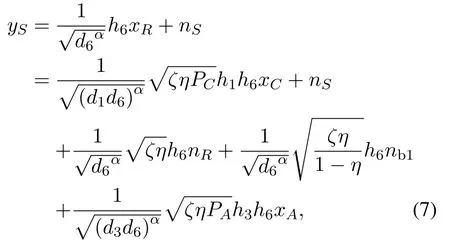
wherens ～CN(0,σ32) is the AWGN at S.Accordingly,signal to interference and noise ratio(SINR)of decodingxCat S can be given by

Where Ξ1=ζη(1-η)d1α|h6|2(|h3|2PA+d3ασ12)+ζηd3α|h6|2σb12+(1-η)(d3d6)ασ32.

During the second stage, B will receive the signals from R, the corresponding signal can be represented as

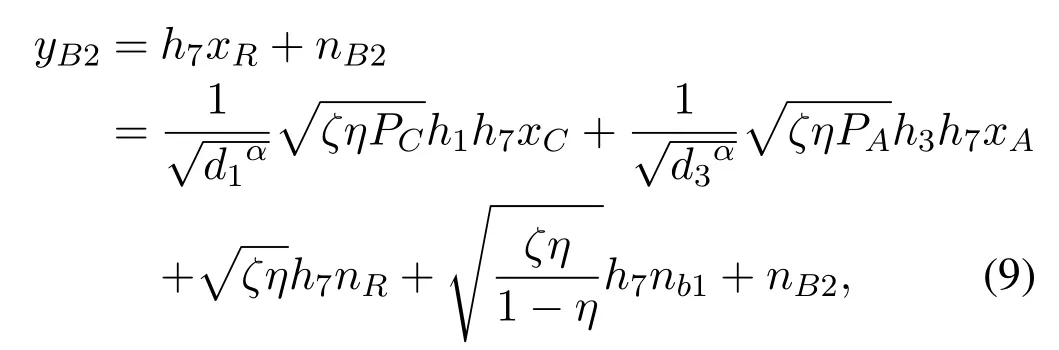
wherenB2～CN(0,σ42) is the AWGN at B.During the two stages, B receives the signals from A, C and R.In order to eliminate the interference ofxC,B performs a subtraction operation on the two stage signals,which is based on the fact that bothyB1andyB2containxc.After removingxCfrom (2), the residual signal at B can be expressed as

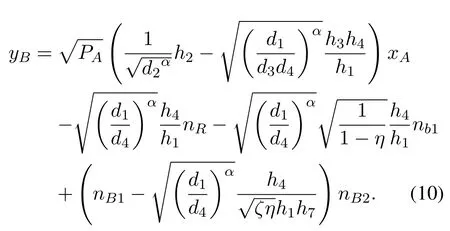
Therefore,SINR decodingxAat B can be given by

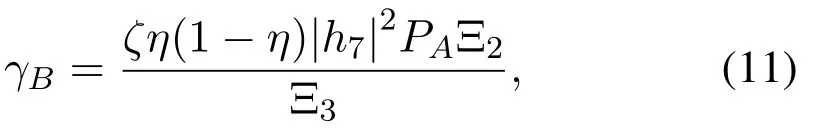
where Ξ2= (d3d4)α|h1|2|h2|2+ (d1d2)α|h3|2|h4|2and Ξ3=ζη(1- η)|h7|2(d1α|h4|2σ12+d4α|h1|2σ22)+d1α|h4|2((1-η)σ42+ζη|h7|2σb12).

IV.PERFORMANCE ANALYSIS

4.1 The Feasibility of the System

The proposed CDTEH has the feasibility of the following three aspects.

1.Spectrum Sharing: the CDTEH we propose allows,directly,D2D users to access to the spectrum of the cellular network to transmit their own information,which improves the efficiency of spectrum utilization.

2.Interference Suppression:the CDTEH gives D2D and cellular users the opportunity to cancel the mutual interference by the two-stage transmission,which develops the channel capacity of D2D pair.

3.Communication Range Extension: the CDTEH arranges a relay node between the cellular users and the base satation, which overcomes the significant attenuation of cellular users due to the long distance.

4.2 The Transmission Rate

Based on the SINRs, the data transmission rates at S and B can be written as

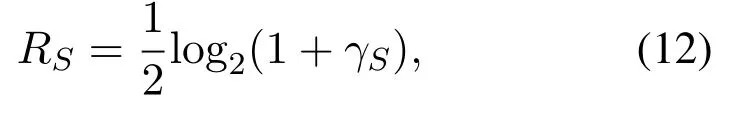
and

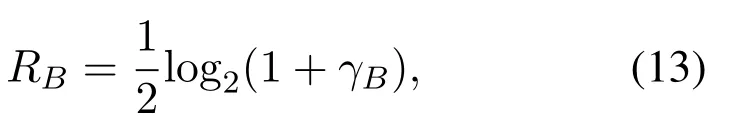
respectively.From above equations, it can be found that the rates at S and B have a non-linear relationship with the ESRη.In particular,whenηreaches a certain value,the rates of S and B will reach an optimal situation,which is shown in Figure 2.In the following,for simplicity of analysis,we assumeσ12=σ22=σ32=σ02andσ42=σb12.

Figure 2 brings to light that the relationship between the data rates and the ESRη.It is observed from Figure 2 that bothRBandRSfirst increase and then decrease with the increasingη.Whenζ=0.4 andη ≈0.7,RBreaches to a maximum value under the circumstances thatRSis greater than the target rate,which corresponds to the optimal solution of optimization problem later in this paper.At that time,the network reaches the optimal transmission state under the proposed CDTEH.From the Figure 2 we can also see that the transmission rates are proportional to the value ofζ.

Figure 3.R-E region EH vs.RS.

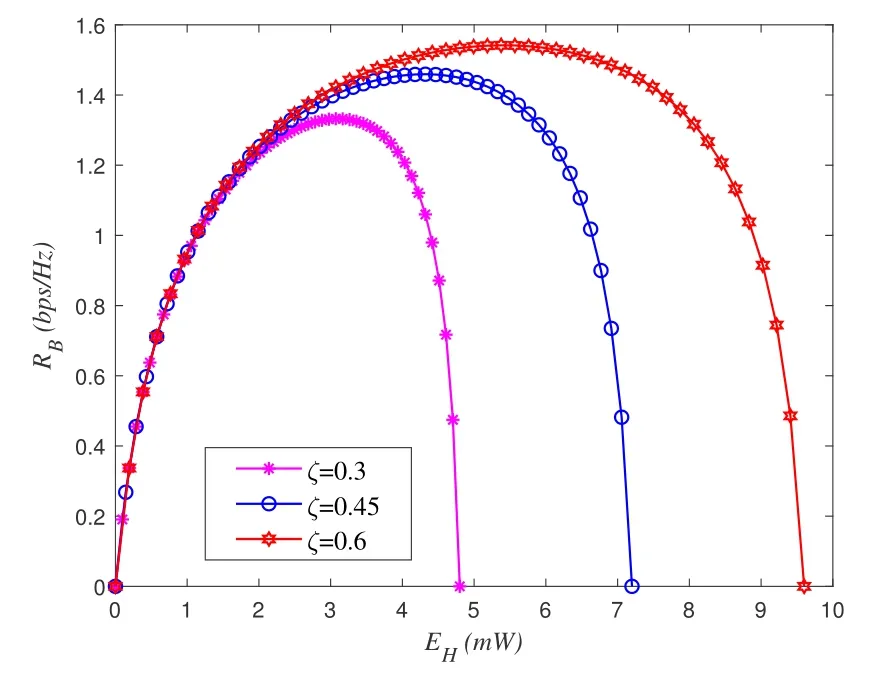
Figure 4.R-E region EH vs.RB.

4.3 Rate and Energy Region

Based on Equ.(4), the average energy captured by R for the information transfer can be given by

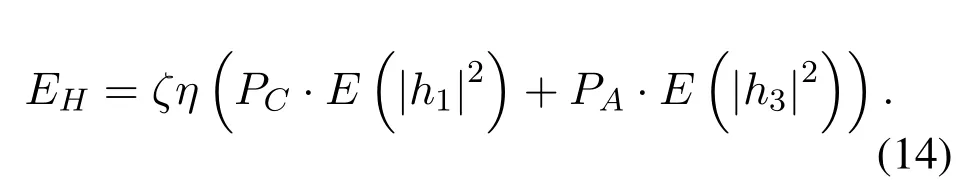
The ergodic sum rate and ergodic capacity at S and B over Rayleigh channel can be written as

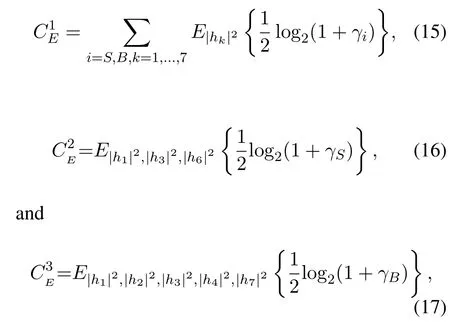
respectively.

Since the energy captured by R has a linear relationship with the ESRη,and at the same time,the ergodic capacityC1E,C2E,C3Eall have a certain non-linear relationship with the ESR.Therefore, there exist tradeoffs in assigning the ESRηto balance maximizing the average harvested energy for energy transfer and maximizing the ergodic capacity for information transfer.To characterize the relationship,the rate-energy(R-E)region is cited here.The R-E region can be defined as follows:

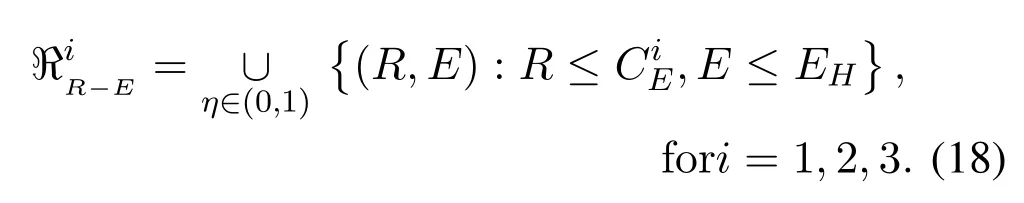
The numerical examples of R-E region are revealed in the Figure 3-5.We can see from the graph that all ofC1E,C2E,andC3Ehave a non-linear relationship with the captured energyEH.The overall trend is thatC1E,C2E, andC3Eincrease to the maximum when the harvested energy increases to a certain value ofEH, and then decrease asEHincrease.Specially,on one hand,R has no energy to transfer information whenη=0.On the other hand, no signal will be forwarded because all the received signals are used for energy harvesting whenη=1.Therefore,in the above two cases,the information transmissions are suspended, and the transmission rates are equal to 0.In addition,it can be observed from Figure 3-5 that the ECE has a positive effect on the data rate, where the ECE is determined by the user’s hardware conditions.Once the ECE is improved, relay will harvest more enregy to relay the signals,which increases the data rate.

Figure 5.R-E region EH vs.C1E.

V.OPTIMIZATION PROBLEM

The data rate is a key factor characterizing the system performance.To improve system performance, we in this paper maximize the data rate,subject to the transmission demand of cellular user.The reasons are as follow.First, improving the data rate can obviously reduce the outage probability of users, which ensures the robustness of the network.Second,increasing the data rate can enhance the energy efficiency of the system and the channel capacity with per unit of energy.Third,in the proposed scheme,an optimal balance between the energy harvesting and the information transfer to maximize is needed, in order to guarantee the benefits of both cellular and D2D users.Based on the above three reasons, we finally optimize the ESR to improve the data rate.We aim to maximizeRB, taking into account the quality of service(QoS)demand of S.Accordingly, the optimization problem can be formulated as

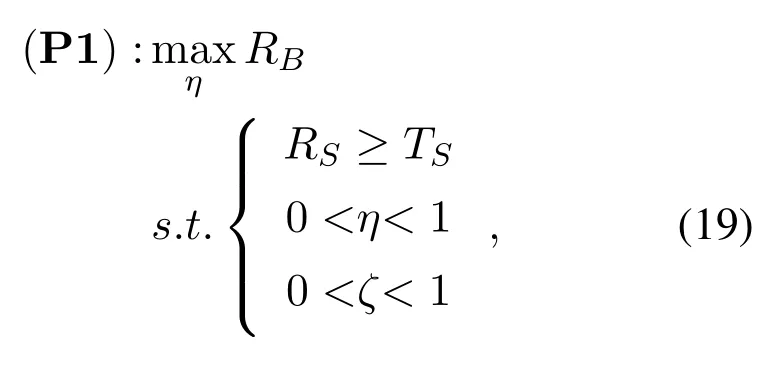
whereTSis the target rate of S.In the light of (12)and(13)and the monotonicity of the logarithmic func-tion,the problem P1 can be converted into

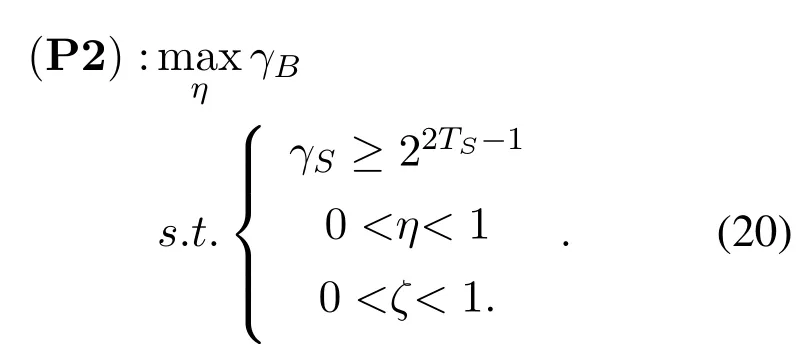
Furthemore,we can reformulate the problem P2 as

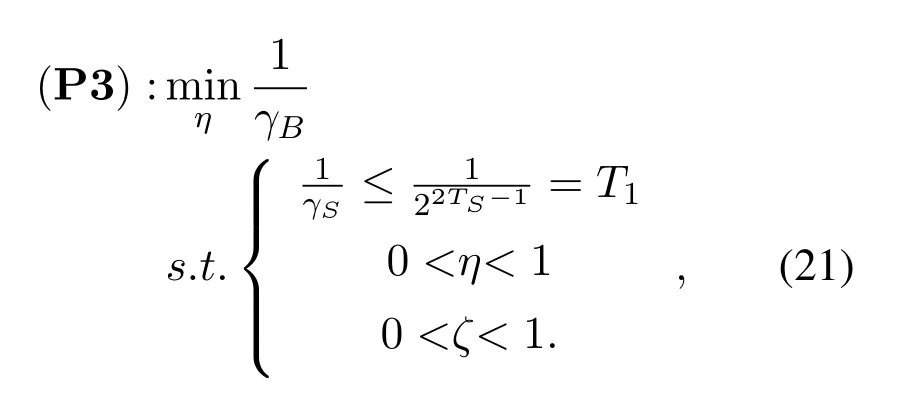
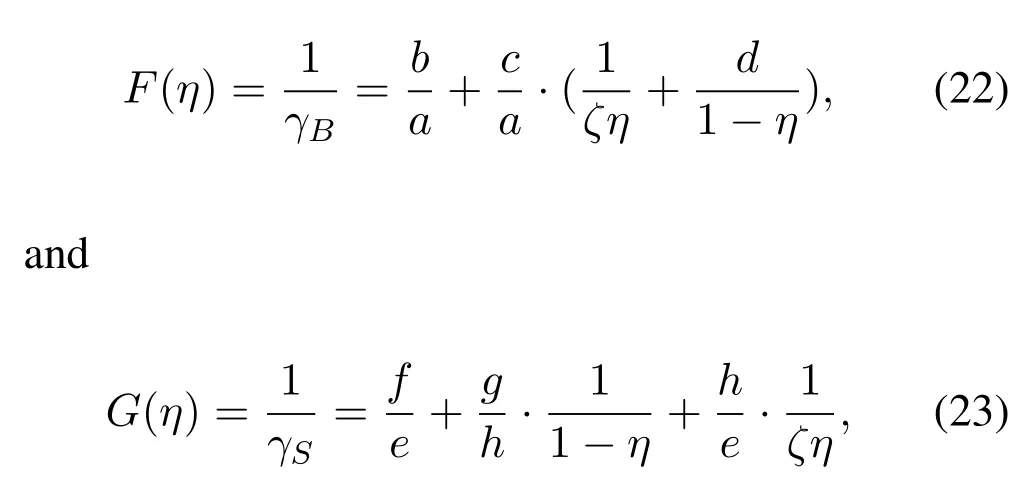
respectively.Where a, b, c, d, e, f, g, h and m are summarized in Table 1.

Table 1.Symbol notations.

It turns out that the problem P3 is a convex optimization problem, as shown in Appendix A.Therefore, it is easy to obtain the optimal solution for the problem P3.First,we construct a Lagrange function given by

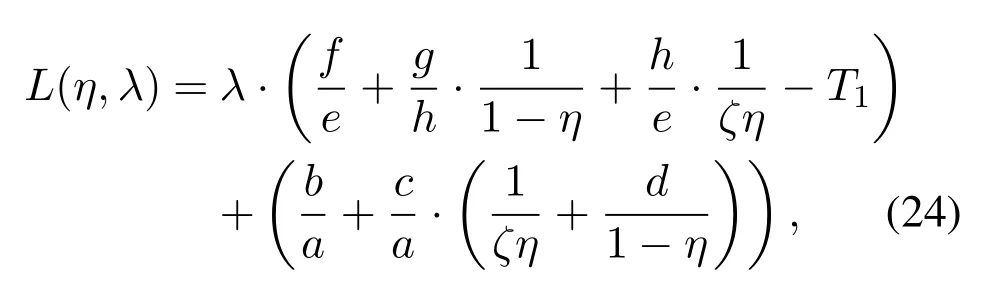
whereλis a Lagrange multiplier.The partial derivative ofL(η,λ)w.s.t.the variableηandλcan be given by

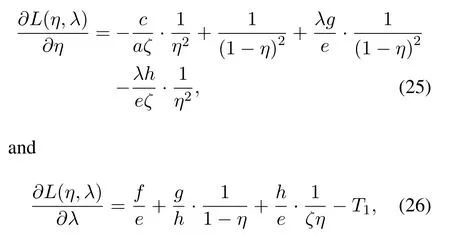
respectively.Based on its KKT condition, lettingwe can acquire the optimal solutionη*optsatisfying the following condition(27).

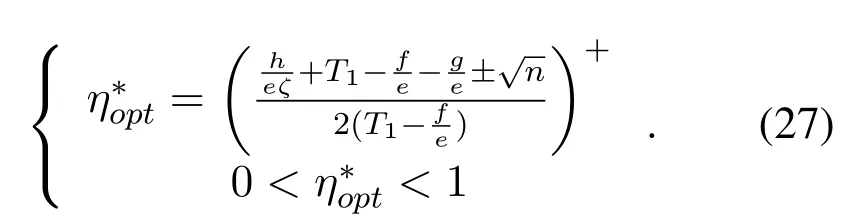
VI.SIMULATION RESULTS

In this section, we will evaluate the performance of the proposed scheme with numerical results.We focus on the effects of the transmit signal-to-noise ratio(SNR), the energy conversion efficiency and the path loss coefficient on the data rate.Additionally,the traditional model without the relay node are reagarded as the benchmark scheme.For simplicity, some of the fixed parameter values in the simulation are summarized in Table 2.

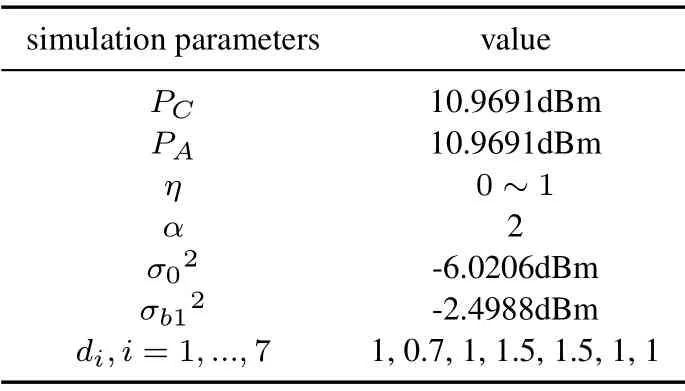
Table 2.Simulation parameters.

Figure 6 shows the relationship between the data rate and the transmit SNR.Obviously, whetherRBorRSis proportional to the transmit SNR.In simulation, the noise power is a constant value, so an increase in the transmit SNR results in an increase in the transmit power,which indicates the amount of energy harvested by R increases.As a result, the forwarding energy of the relay gets more,which increases the recognition degree of the signals at the receivers and improves the system performance.What is even more important is that we can,clearly,see from the Figure 6 that the data rate of the proposed scheme is greater than that of the benchmark scheme, which indicates that the proposed scheme ameliorates the system performance as compared with the benchmark mark.

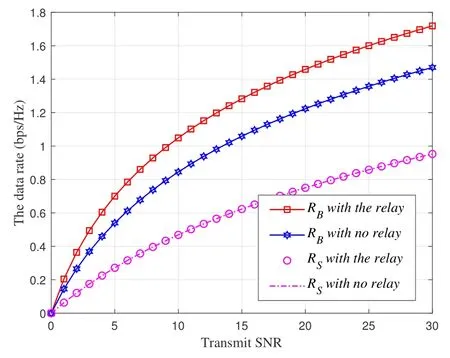
Figure 6.The relationship between the rate and the transmit SNR.

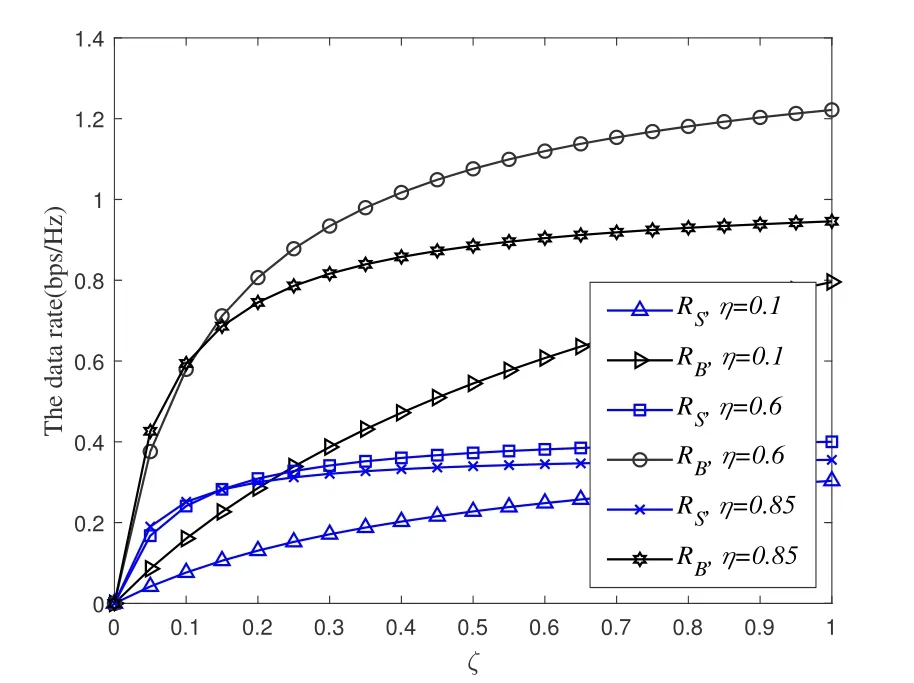
Figure 7.The relationship between the rate and the ECE ζ.

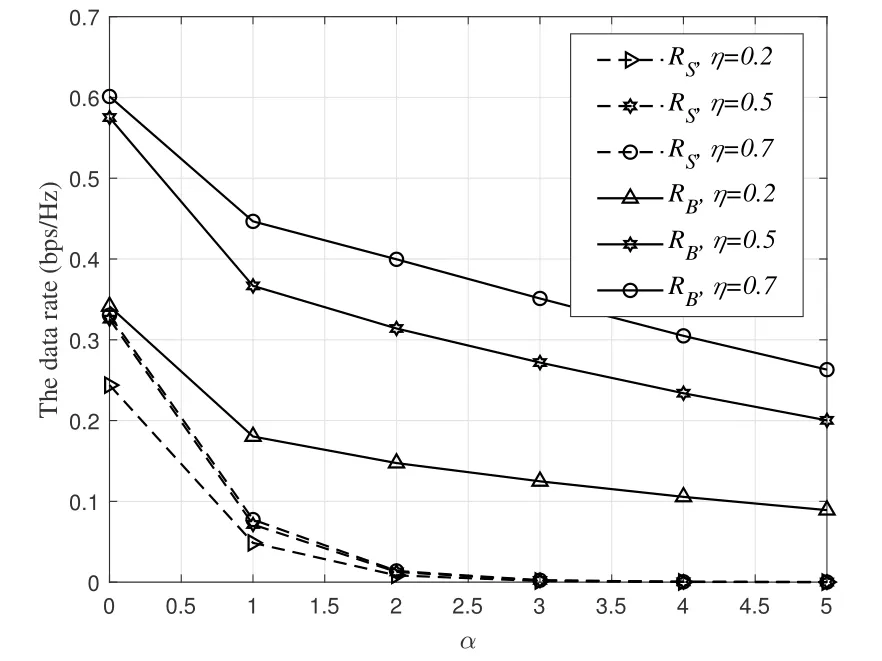
Figure 8.The relationship between the rate and the path loss coefficient α.

Figure 7 depicts the impact of energy conversion rate on the data rate.The energy conversion ratioζdetermines which part of energy can be harvested by the relay node and used to transfer the signals.Therefore,a higher energy conversion ratioζmeans that more energy is harvested, and thus the transmitting power of the relay node increases.As a result,the SNR and the receiving rate at the receivers increase and thus the outage probability will decrease.

Figure 8 brings to light that the path loss coefficient has a fatal impact on the data rate.We can find from the Figure 8 that the forwarding energy of the relay recudes greatly if the path loss coefficient is large.In the Figure 8,as the path loss coefficient is equal to 5,the rate is almost close to 0.Therefore,we should first estimate the path loss before information transmission.

VII.CONCLUSION

In this paper,we proposed an collaborative D2D transmission scheme with energy harvesting in a cellular network, where D2D pair were allowed to access the spectrum of cellular network to transmit their own information.Particularly, both cellular and D2D users would benefit it,in which the relay expanded the cellular communication range and helped D2D and cellular users to remove the mutual interference.To evaluate the system performance, R-E region was introduced and an optimization problem was formulated.Finally,numerical results validated the proposed scheme.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China under Grant No.62071373, in part by the Innovation Talents Promotion Program of Shaanxi Province under Grant No.2021TD-08, and in part by the China Scholarship Council.

APPENDIX

PROOF OF CONVEXITY OF OPTIMIZATION PROBLEM P3

We consider the second order derivative of functionF(η) andG(η) to prove its convexity.According to(22),we have

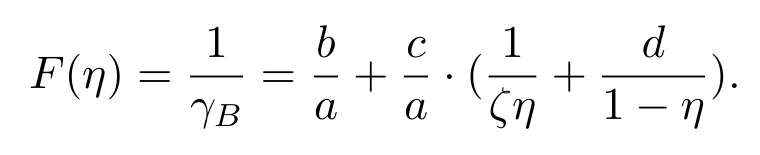
The first-order derivative of(22)w.r.t.ηcan be written as

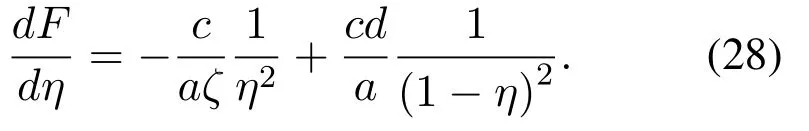
And the second-order derivative of(22)w.r.t.ηcan be given by

According to the Table 1,we haveFor any discreteη ∈(0,1), it always seem to occur thatTherefore,we have

Similar toF(η),G(η) is also satisfied with (31) for any discreteη ∈(0,1)