Cooperative Caching for Scalable Video Coding Using Value-Decomposed Dimensional Networks

Youjia Chen,Yuekai Cai,Haifeng Zheng,Jinsong Hu,*,Jun Li

1 Fujian Key Lab for Intelligent Processing and Wireless Transmission of Media Information,College of Physics and Information Engineering,Fuzhou University,Fuzhou 350000,China

2 School of Electronic and Optical Engineering,Nanjing University of Science and Technology,Nanjing 210000,China

Abstract: Scalable video coding (SVC) has been widely used in video-on-demand(VOD)service,to efficiently satisfy users’different video quality requirements and dynamically adjust video stream to timevariant wireless channels.Under the 5G network structure, we consider a cooperative caching scheme inside each cluster with SVC to economically utilize the limited caching storage.A novel multi-agent deep reinforcement learning (MADRL) framework is proposed to jointly optimize the video access delay and users’ satisfaction, where an aggregation node is introduced helping individual agents to achieve global observations and overall system rewards.Moreover,to cope with the large action space caused by the large number of videos and users, a dimension decomposition method is embedded into the neural network in each agent, which greatly reduce the computational complexity and memory cost of the reinforcement learning.Experimental results show that:1) the proposed value-decomposed dimensional network (VDDN) algorithm achieves an obvious performance gain versus the traditional MADRL;2)the proposed VDDN algorithm can handle an extremely large action space and quickly converge with a low computational complexity.

Keywords:cooperative caching;multi-agent deep reinforcement learning; scalable video coding; valuedecomposition network

I.INTRODUCTION

With the rapid development of wireless access technology and mobile devices,a 9-fold increase in video traffic is predicted by 2022, making the mobile video traffic to account for 79% of total mobile traffic [1].How to deal with the various user requirements on video quality and improve the user experience on video-on-demand (VOD) service have become a key issue of wireless communications.

As a promising technique to reduce the duplicated data transmission, edge caching has received considerable attention by pre-storing anticipated popular content in network nodes near mobile users.Multiple wireless caching strategies have been proposed in recent years, such as proactive caching and coded caching[2].Among them,cooperative caching inside a cluster jointly utilizes the storage in multiple closeconnected devices,and takes the advantage of the similar preference among users in one region or group[3].

Furthermore,the analysis of caching strategy should also consider the characteristics of video files, for instance,some works focused on short videos[4].Currently,to efficiently satisfy different user requirements and dynamically adjust the video quality with fluctuant network environments.Scalable video coding(SVC) has received much attention for video transmission over wireless due to its flexibility [5, 6].As indicated in[5],it particularly benefits from the wireless network architecture with edge resources (e.g.,caching or computing)[6,7],and improves the bandwidth utilization and the user experience[6,8].In recent years, SVC has been commonly used in many video service, such as tele-conferencing, live Internet broadcasting, and video surveillance [9].SVC encodes a video into ordered layers: one base layer,layer-1,with the lowest playable quality,and multiple enhancement layers,layer-i,i ＞1,that gradually improve the video quality based on previous layer-(i-1).Compared with traditional video coding[10,11],SVC significantly reduces the storage by sharing the lower layers across different video qualities, and handily manages the video quality by controlling enhancement layers.

Considering the architecture of 5G radio access networks,where multiple base stations(BSs)are grouped and share a mobile edge computing(MEC)server,the cooperative caching scheme becomes a natural choice.Since MEC servers are in close physical proximity of the wireless end devices, which can provide the mobile users storage and computing resources with an extremely low transmission cost [12, 13].Moreover, combining SVC with cooperative caching can more efficiently utilize the limited storage and easily satisfy the various video requirements from users.However,the practical world environment is generally non-stationary due to the changes in dynamic environments, this combination poses a serious challenge to the strategy formulation of wireless networks.Hence,this work focuses on the topic,and the artificial intelligence(AI)approach is chosen to achieve a robust and low-complexity strategy suitable for the large complex decision problem.

In this work, the SVC-based caching strategy and the video quality service strategy are jointly optimized, which aims to simultaneously minimize the video access delay and maximize the user’s satisfaction.Inspired by the cluster-based structure of current 5G mobile network,a low-complexity reformative multi-agent deep reinforcement learning(MADRL)is proposed to efficiently and quickly obtain the optimal strategies.Main contributions of this work can be summarized as:

· A value-decomposed dimensional network(VDDN)algorithm is proposed to solve cooperative caching problem,where a value-decomposed dimensional network is employed in an aggregation node for a globe observation and overall system reward.Experimental results show an obvious performance gain compared with the traditional MADRL.

· Considering the high computational complexity and memory usage due to the large size of action space in reinforcement learning, a dimension decomposition approach is embedded into the dueling deep Q-network in each agent.By decomposing the large action space to multiple independent sub-action spaces.

II.RELATED WORK

2.1 Traditional Content Cache

Traditional content cache technology is mainly considering the user’s requests as the main content of the cache, such as least frequently used (LFU) algorithm [14], which uses a counter to record the frequency of the data content is accessed, and the least frequently used data will be removed in the caching queue.Similarly,there is also existing the first-in firstout(FIFO)algorithm[15]and the least recently used(LRU) algorithm [14].Among them, the core principle of FIFO is that a file should be the first to be eliminated if it is the first one to enter the caching,while LRU stores the contents of recently used data near the top of the caching queue and the data accessed earlier is removed from the bottom of the cache.These traditional algorithms have limited performance improvements, even if some efforts have been made to optimize them, such as the adaptive replacement cache (ARC) algorithm [16], which tracks both LFU and LRU to get the best use of the available caches.

Some researchers have implemented proactive caching in the 5G scenarios before the rise of artificial intelligence technology.In [17], a proactive caching platform for 5G networks was built to alleviate backhaul congestion through caching files during off-peak periods and the authors in[18]modeled the proactive caching problem as a cache management one to attain optimal video quality.In [19], the authors designed caching algorithms for multiple network operators that cooperate by pooling together their co-located caches,in an effort to aid each other, to avoid large delays due to fetching content from distant servers.However,these works are not suitable for situations where the transition probability of the system is difficult to obtain.

2.2 DRL-based Content Cache

With the rapid development of artificial intelligence in recent years, researchers no longer limit the research of cache technology to the traditional optimization technology.Instead, they focus on the excellent decision-making ability of deep reinforcement learning(DRL).As a branch of artificial intelligence,DRL enables caching devices to learn from original environmental requests to realize content popularity awareness and intelligent caching decisions.Many benchmark algorithms for deep reinforcement learning, including deep q-network (DQN) [20], dueling DQN[21],actor-critic[22],etc.,had been proven that had better performance compared to the traditional content cache technology.The author in [23] proposed an external memory for revising theq-value to enhance the DQN caching performance.In [24], knearest neighbor(KNN)was embedded into the actorcritic framework to achieve improved short-term cache hit rate (CHR) and stable long-term CHR.However,Future wireless communication networks require to support exploding mobile traffics, real-time analysis and agile resource management, which are challenging due to the increasingly complex and dynamic environments[2].The entities in communication networks cannot be isolated from others,above single-agent algorithms can no longer effectively applied to practical wireless network scenarios.

Therefore, researchers had turned their attention to the field of MADRL which developed from the traditional independent q-learning (IQL) algorithm.In discrete action control, the value decomposition network(VDN)and Qmix algorithms had been produced in [25, 26], while in continuous action control, algorithms such as multi-agent actor-critic (MAAC) and multi-agent deep deterministic policy gradient(MADDPG) had been developed [27, 28].These algorithms allow agents to cooperate with each other, to take the advantage of this feature, the work in [29]used MAAC framework to cope with the cooperative caching in wireless network, and in [30], the author applied MADDPG and compared the performance in three cooperative scenarios.

Regrettably,the above works had avoided the problem of computational complexity.Although the wolpertinger framework in[24]leveraged prior information about the discrete actions in order to embed them in a continuous space, the method may not be suitable for fields with natural discrete action spaces,such as our wireless cache scenarios.In these fields,the assumption of continuous correlation of action spaces should not be imposed.Therefore,the caching decisions made for the data contents in the simple environment are difficult to be directly applied to the practical scenarios and produce good benefits.How to further utilize these edge data cache algorithms of artificial intelligence to achieve low complexity, strong convergence and improve their practical application value is an urgent problem to be solved.

III.SYSTEM MODEL

3.1 Network Scenario

As illustrated in Figure 1,we consider a wireless edge video caching architecture consisting of multiple BSs and users.Following the network deployment strategy in current 4G and 5G networks [31, 32], a number of BSs are grouped as a cluster and connected to an aggregation node, then to the core network.The aggregation node not only includes a traditional gateway, wireless access point controllers and centralized resource management modules,but also provides storage and computing resources to users,known as MEC servers.The existence of MEC servers the provides foundation for the learning-based cooperative caching strategy.

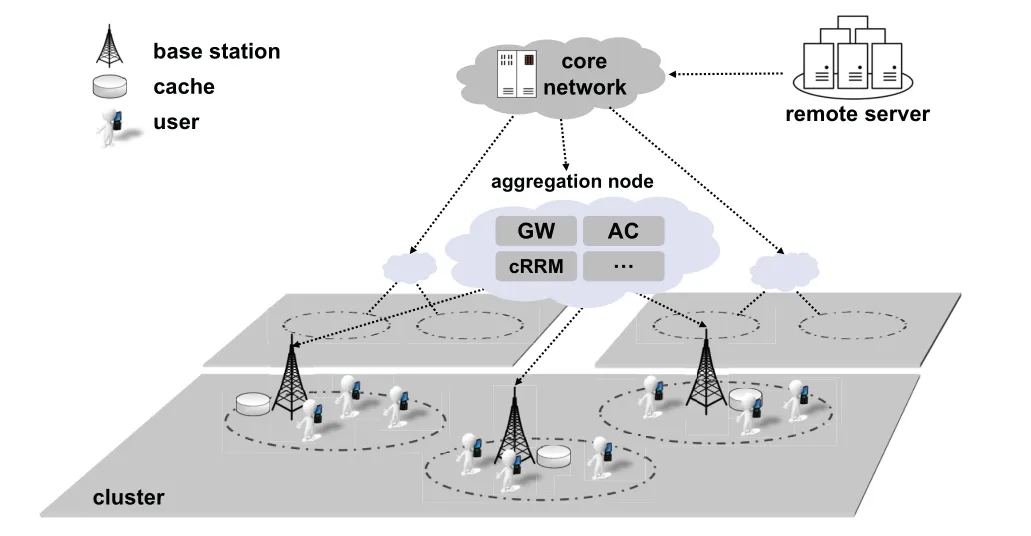
Figure 1.An illustration of cluster-based wireless cellular networks.

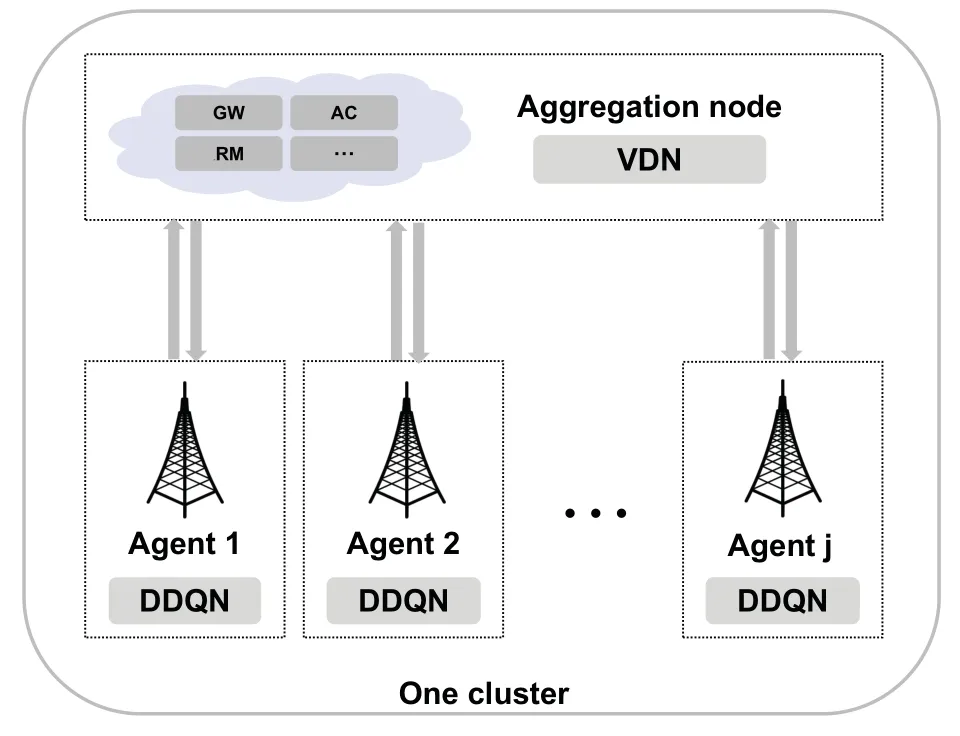
Figure 2.Multi-agent layered video streaming caching framework.

Let us consider a cluster which involvesJcacheenabled wireless BSs andIusers,denoted by the setsJ≜{1..j..J}andI≜{1..i..I},respectively.Under the basic one-user-on-BS association criterion [33],we denote byUjthe set of users associated with BS-j.Meanwhile,considering the storage resources on each BS,we denote the storage size of BS-jbyZj.

As mentioned before, in this work we consider an edge video caching system.If the requested video of a user is cached in its serving BS, the video file can be transmitted to the user directly.If not, the serving BS will seek help from other BSs in the same cluster under the coordination of the aggregation node.While the video is not cached in any BS of this cluster,the remote server has to be connected through the core network.

3.2 Files with Scalable Video Coding(SVC)

We consider a video library,V≜{1..v..V},in which each video file is encoded using SVC with aim at flexibly providing various video quality to satisfy different user preference and adapt to time-variant network environments.

To provideKquality versions of a video,SVC has to encode the video intoLlayers,whereL=K.Denoted byL≜{1..l..L}the video layers,it includes a basic layer,i.e.,l=1,andL-1 enhancement layers.

Generally, a higher quality level of a video leads to a larger file size and needs a larger transmission rate[11].Under SVC scheme,to satisfy thek-th quality version, 1≤k ≤K, the corresponding file size of thev-th file can be calculated aswherefvldenotes the file size of thel-th layer of thev-th video.

3.3 Video Caching and Delivery

As mentioned above,with SVC,an encoding layer of a video file, instead of a video file, should be considered as the caching unit.We useδjvl= 1 to indicate that thel-th layer of thev-th video is cached in BS-j,otherwise,δjvl=0.Considering the storage limit,we have

Meanwhile,to represent the user requirement,a binary variableλiv≜{0,1}is used to indicate whether user-irequests thev-th video.Since each user can only requests one quality about a specific video in a time slot,we haveDue to the fluctuation of wireless network,the user requirement on video quality can not always be satisfied.Generally the network will decide the served video quality ˜kivof user-iabout thev-th video according to the current network environment.Givenkivthe required video quality of user-iabout thevth video,we have the network served video quality is 1≤≤kiv.

Note that, to service a user with a video quality,all the video layersl ≤should be delivery due to SVC.With edge caching, the video delivery involves three cases:

·Local Hit: When the required video layer is cached in the user’s serving BS, it will be transmitted directly to the user.In such case, the file transmission only involves the wireless link between the BS and the user, which contributes an extremely small video access delay [19].Here,we denote byd0the unit access delay of local hit.

·Cluster Hit: When the required video layer is cached inside the cluster but not in the user’s serving BS,the required layer will be transmitted via the aggregation node to the serving BS first,then to the user.In such case, we denote bydjj′the unit access delay of the transmission from BS-j′to the user via serving BS-j.

·Service From Remote Server: When the required video layer is not cached inside the cluster, the required video layer has to be achieved from the remote server.Similarly,djdenotes the unit access delay in this case.Since such transmissions are many-fold further than that inside one cluster,we havedj ≫djj′ ＞d0[34].

For convenience,the notations used in this paper are summarized in the following Table 1.

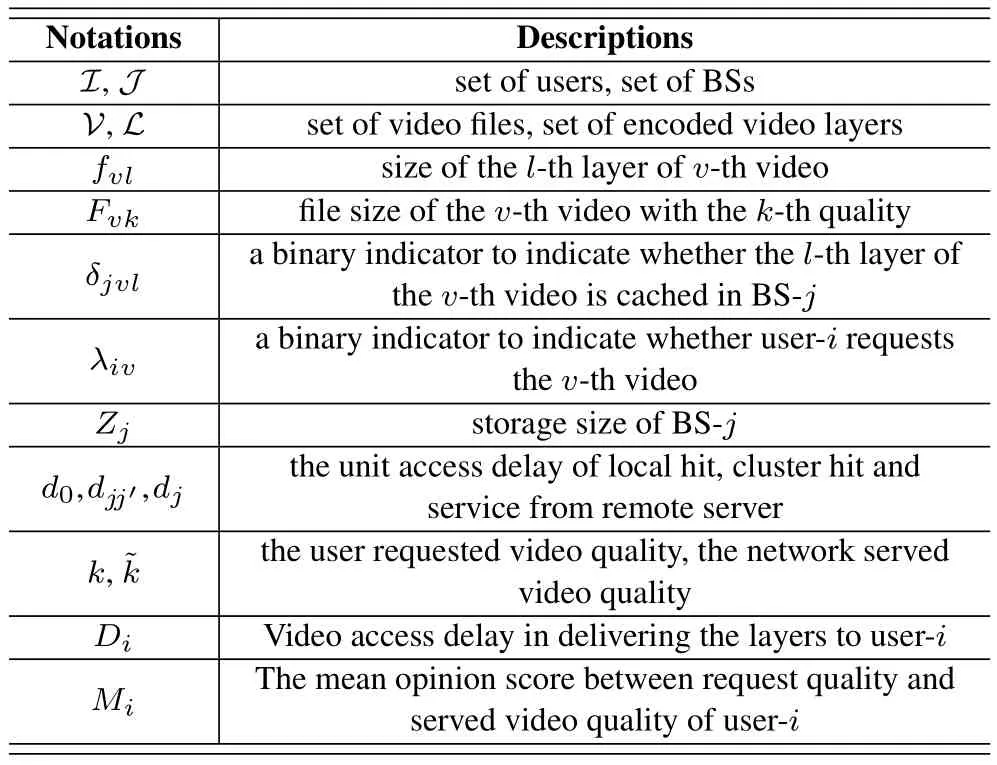
Table 1.System notations and their descriptions.

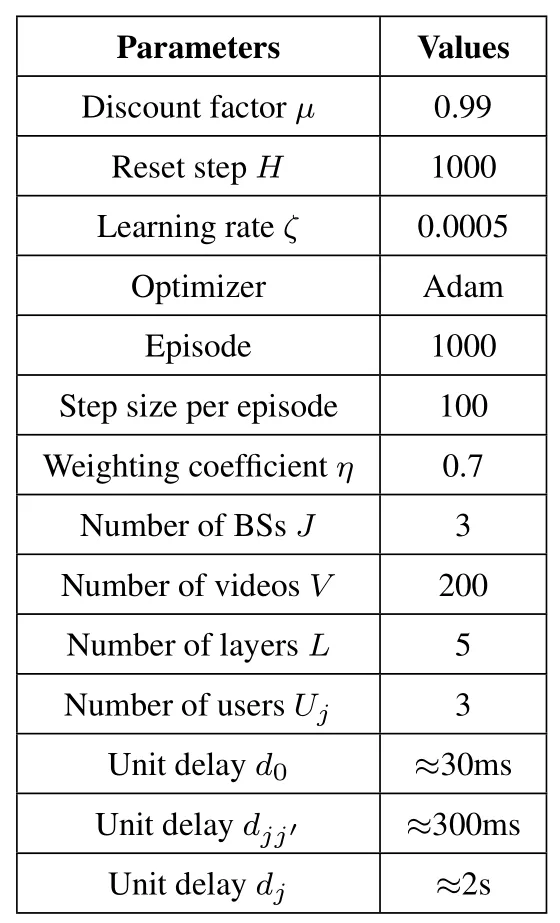
Table 2.VDDN parameter descriptions.

IV.PROBLEM FORMULATION

In this section, we investigate the performance metric for a VOD service.Generally, from the perspective of the network, the video transmission delay or the backhaul cost is viewed as the performance metric of a caching strategy.Explicitly,a better caching strategy places the contents nearby the requesting users,hence requires less transmission via backhaul links and backbone network, resulting to a smaller transmission delay.On the other hand,from the perspective of users, their experience towards videos (a.k.a QoE)relates to several factors, such as video’s bitrate, the initial delay before playback, the probability of interruption during playback,etc.[35].Jointly considering these two aspects,in this work,the video access delay and the video served quality are selected as the system performance metric,since the former reflects both the network performance and users’experience under the caching strategy and the latter reflects the users’satisfaction due to the network service decision.

4.1 Video Access Delay

The video access delay reflects the time it takes for a user to achieve all the layers needed,which measures the time that the users have to wait before accessing video[36].

When user-irequests thev-th video through its serving BS-j,and the network serves the ˜k-th quality,the video access delay can be formulated as

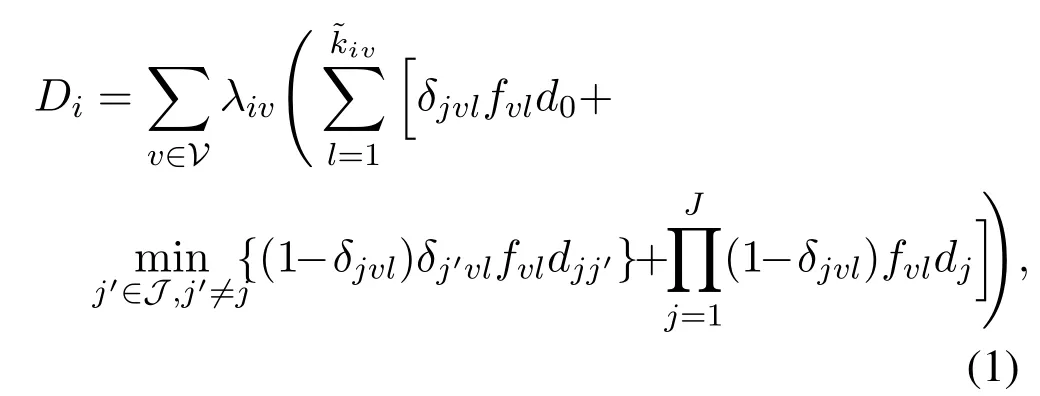
The first item in brackets,i.e.,δjvlfvld0,denotes the access delay when a local hit occurs.The second and third items denote the access delay of cluster hit and service from remote server, respectively.Note that,min{·} in the second item means that the BS in the cluster providing the minimum delivery delay will be selected,when the video layer is cached in more than one BSs.

4.2 Mean Opinion Score(MOS)

The MOS measures the video quality related to the video’s bitrate, which is an important part of users’satisfaction during the process of interactions in video service[35]

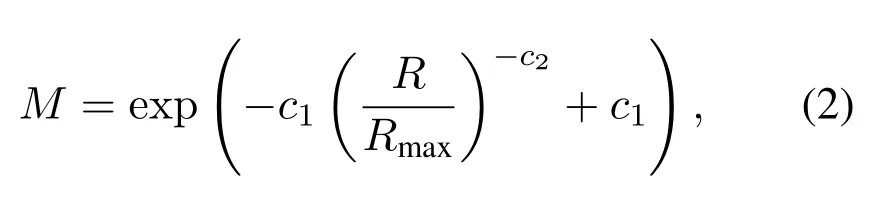
wherec1= 0.16 andc2= 0.66 are coefficients,Rdenotes the video bitrate received by the user, whileRmaxrepresents the bitrate of the video with its best quality.It has 0＜M ≤1,and a largerMrepresents a better video quality achieved.Fundamentally, it reflects the quality gap between the achieved video and the best video.

In our scenario, user-imay be served with a lower video quality than it requests, i.e.,≤kiv.This quality gap experienced by users can be measured with MOS.The MOS for user-ican be calculated as:

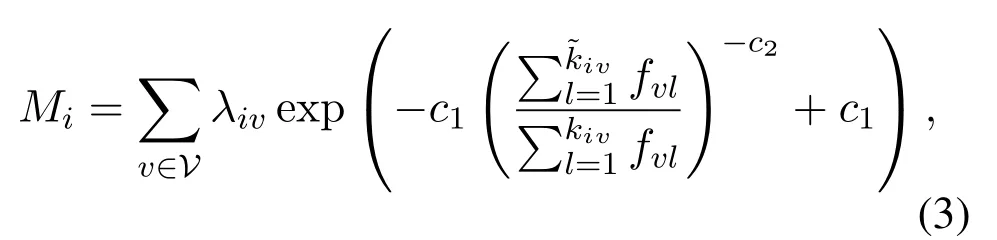
where we use the ratio of the video file size to calculate the ratio of the video bitrate, since the video file size is generally linearly proportional to the average video bitrate.

4.3 Multi-Objective Optimization

Jointly consider the delay and the user satisfaction above, a multi-objective optimization problem is proposed here.In more detail, the caching strategy in a cluster,δjvl,and the video service strategy,,should be optimized simultaneously to minimize the video access delay and maximize the MOS.

By introducing a weighting coefficientη,a weighted linear combination objective function can be formulated as

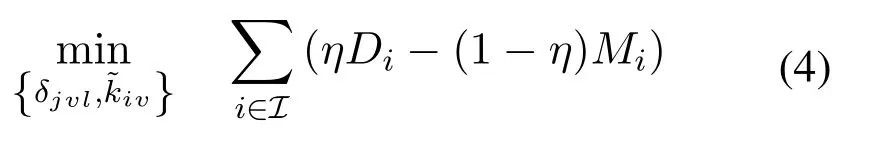
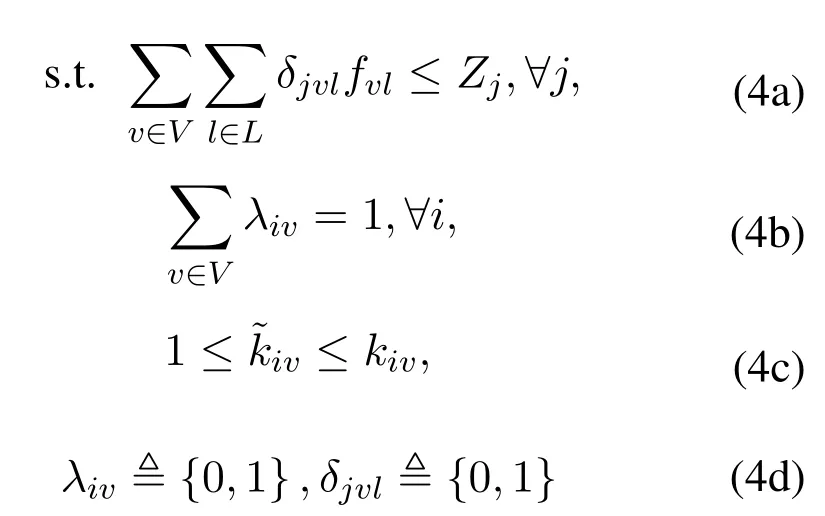
where Eq.(4a) represents the limit of storage size,Eq.(4b)represents that each user can only request one video file in a time slot and Eq.(4c) represents that served quality is lower than the user’s requested quality.

V.COOPERATIVE CACHING FRAME WORK BASED ON MULTI-AGENT DEEP REINFORCEMENT LEARNING

For the above problem, the caching strategy and the video service strategy should be globally optimized in the entire cluster, but not locally inside one BS.Hence, a MADRL-based cooperative caching framework is proposed in this section.

In this framework as illustrated in Figure 2, each BS works as an agent which is equipped with a dueling deep Q-network (DDQN), and the aggregation node works as training center which is equipped with a value-decomposition network(VDN).The message transferred between each agent and the training node is transmitted through the backhaul link between each BS and the aggregation node.With such framework,the local observation obtained by each agent can be integrated in the aggregation node, which results to a better performance than fully independent agents or centralization[25].

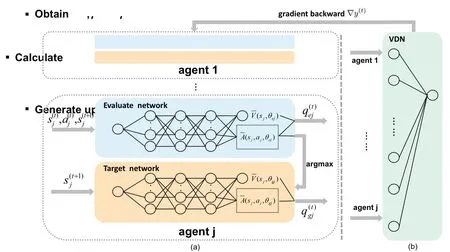
Figure 3.The proposed DDQN and VDN network structure.

Generally, the aim of reinforcement learning is to find the optimal policy to interact with the environment.Briefly speaking,a policyπcan be viewed as a mapping function from a perceived statesto an actiona.That is,a=π(s).In our MADRL framework,denoted byπ≜{πj,∀j}the joint policy for all agents,the optimization problem proposed in Eq.(4) can be transformed as:

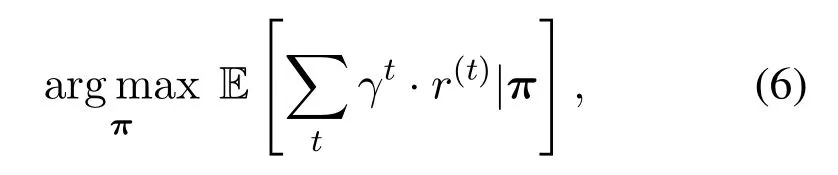
whereγis the attenuation coefficient,rdenotes the reward function,tdenotes the index of the time slot,t ∈{1..t..T},and E[·]denotes the expected value.

5.1 Individual Agent with DDQN

In reinforcement learning, each agent independently receives state from environment,and selects a specific action to interact with the environment.In our framework,each agent will also receive updated information from the aggregation node and then adjust its actions with these global information.

Specifically,in the video delivery phase,each agent,i.e.,a BS,decides the appropriate served video quality when receives the users’ request.And in the video caching phase, each agent has to decide which video content has to be cached in local storage.

Fitting the caching scenario in the reinforcement learning[37], the state space and action space for thej-th agent,i.e.,BS-j,can be constructed as follows:

· State space Sj:The state space involves the received video requests from its users, and the file layers cached in its storage.In a time slott,a state vector can be defined as

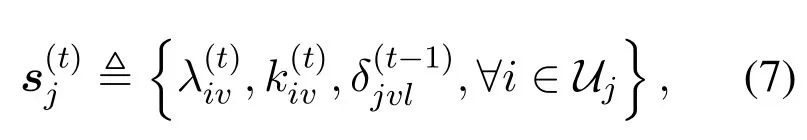
· Action space Aj:The action space includes the caching strategy and the served video quality for users.In a time slott, the action vector can defined as

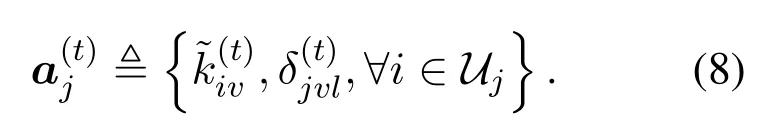
As illustrated in Figure 3(a), a DDQN is employed in agent-j, which includes two neural networks: one is evaluate network with parameterθej, and the other is target network with parameterθgj.

Both of the neural networks include two branches:one estimates the state-value function ¯V, while the other one estimates the advantage action function ¯A.They are used to calculate the actionq-value function[21]:

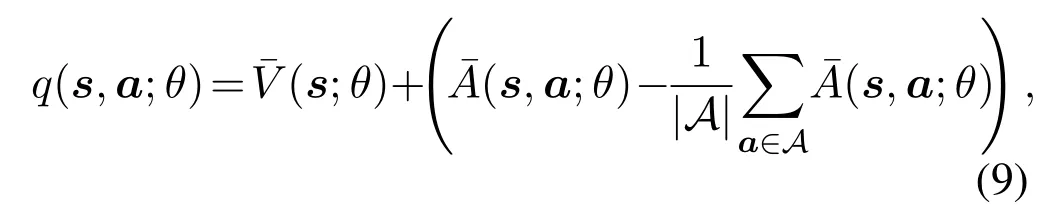
where|A|denotes the size of action space.

In the evaluate network with parameter, theqvalue is calculated as

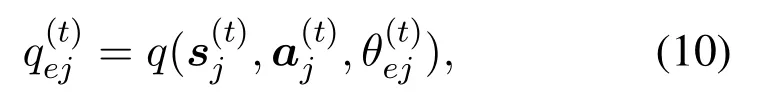
and then choose the action for the next state with the maximumq-value,i.e.,

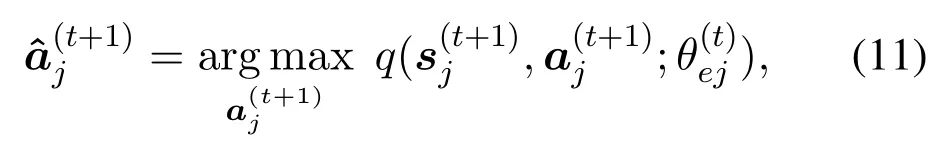
In the target network with parameter, theq-value with the chosenis calculated as

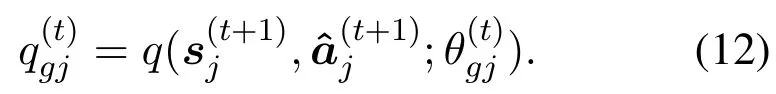
At last, the obtainedq-values from the two networks will be sent to the aggregation node.

Note that,different with traditional MADRL framework, due to the presence of the training node, each agent no longer needs to calculate the rewards.Instead,the parameter for the evaluate network,θej,will be updated according to the gradient of the loss function sent back by the aggregation node, i.e.∇y(t)in Eq.(19).That is,

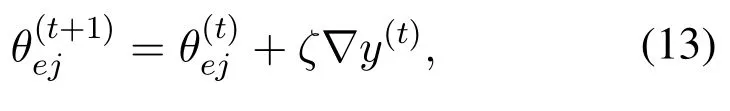
whereζdenotes the learning rate.In contrast,the parameter of the target network,θgj, is updated periodically by copying the parameter of the evaluate network,θej[20].

5.2 Aggregation Node with VDN

As shown in Figure 3(b),a VDN employed in the aggregation with aim to achieve a global perspective for the whole system, which collects the state and action information from all cooperative agents to calculate the system reward, then generates the corresponding updated information and sends it to the agents.

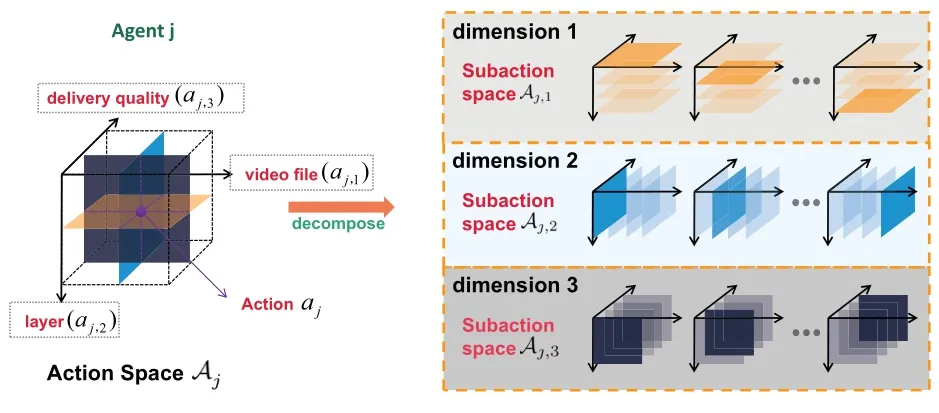
Figure 4.An illustration of the proposed dimension decomposition structure.

Specifically, in time slott, a joint state and a joint action are generated in aggregation node with the information provided by each agent.That is,

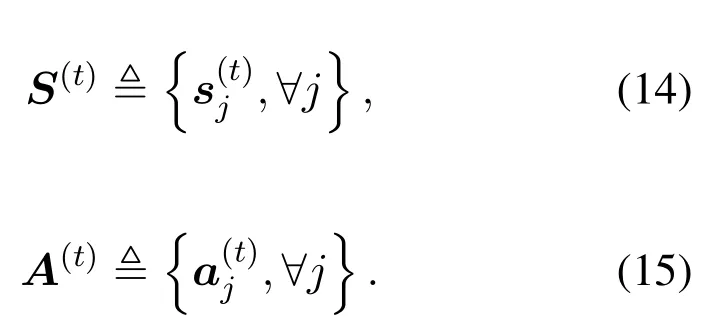
With this global state and action information,the aggregation node could calculate the overall video access delay and MOS for the system, i.e., the optimization objective in Eq.(4).Under the framework of reinforcement learning,we define the system reward based on this objective function.That is,

· Reward functionr: The system reward includes two performance metrics, i.e., the video access delay and the MOS.Since the reinforcement learning aims to maximize the reward for the whole system,we define the system reward in the time slottas

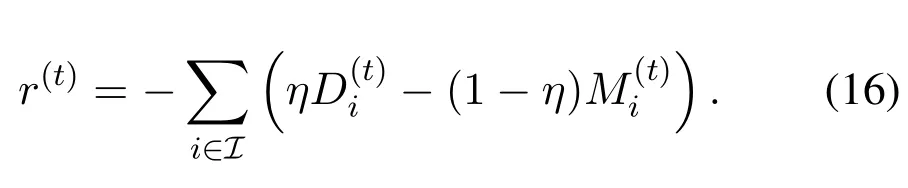
Moreover, with the receivedq-values mentioned above, the VDN calculates the jointq-values of the entire system, i.e.,and, can be calculated as[25]

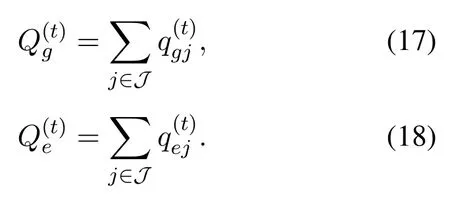
Furthermore,combining the jointq-value and the reward,the loss functionyand the corresponding gradient of this loss function can be obtained as follow:

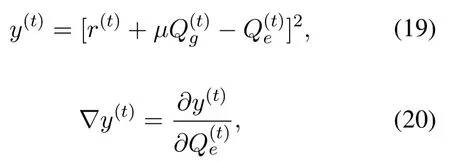
whereμ ∈(0,1) denotes the discount factor,∇denotes the gradient.

The obtained gradient∇y(t)will be sent back to each cooperative agent for neural network updating,i.e.,Eq.(13).

After sufficient iterations,the parameter of the neural network in each agent,θej,will converge to a stable value,which contributes to the optimal policyπj.For the entire system,the optimal joint policyπfor Eq.(6)can be achieved.

VI.DIMENSION DECOMPOSITION TOREDUCE THE SIZE OF ACTION SPACE

The large size of action space not only poses a big challenge to the storage space of computer, but also leads to high computational complexity.To solve this problem,in this section,the concept of dimension decomposition is introduced in our MADRL framework to reduce the size of action space[38].

As mentioned in Eq.(8), the action space in each agent includes the video and the layer selection,,and served quality selection for each user,.In practical scenarios,the large number of popular video files, the various video qualities for different devices,the large number of users and their fast-changing demands, and the time-variant wireless environment all contributes to the exponentially growth of the action space.

In this work, we break down the action space in agent-j,Aj,into three independent sub-action spaces as shown in Figure 4.

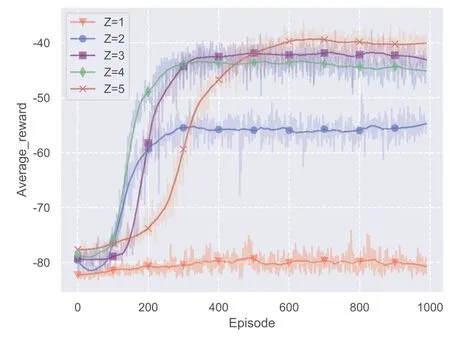
Figure 5.Impact of different storage size.

·Aj,1with the actionaj,1≜{δjv}: it denotes the video selection from a video libraryVwith a size|V|=V.

·Aj,2with the actionaj,2≜{δjl}: it denotes caching video layer selection fromLlayers.

·Aj,3with the action: it denotes served quality selection fromKvideo quality versions.

Assuming that each BS can cacheZjvideo layers,then the size of original action spaceAj,is given by

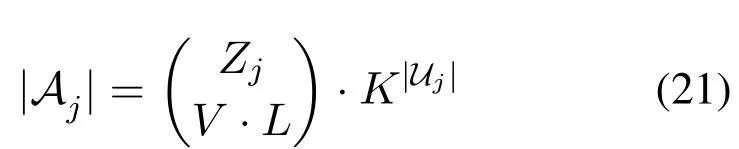
which means that BS-jshould choose from the overallV ·Lvideo file layers and decide the quality served for each associated user,i.e.,Uj.In contrast,with the dimension decomposition,the size of action space when each BS only cache one video file can be easily calculated as

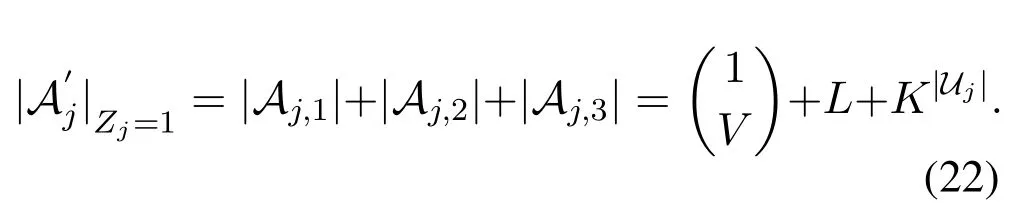
Hence, when each BS is allowed to cacheZjvideo layers,Eq.(22)will be extended to the general case asfollow,

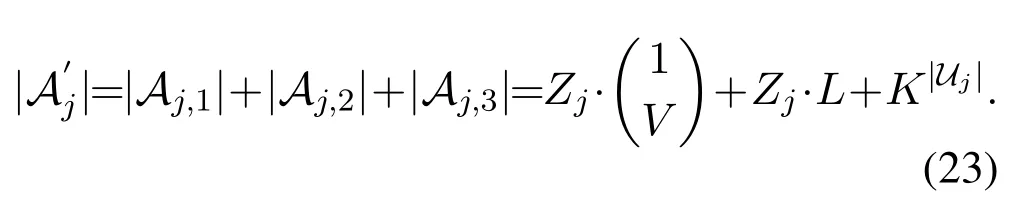
Here, in the algorithm each cache space will be allocated to a branch of neural network, and the constraint that no same video layer will be cached simultaneously can be easily satisfied in the algorithm.From Eq.(23),it can be seen that the number of action spaces also grows linearly as the cache storage grows.Compared with Eq.(21), the dimension decomposition algorithm greatly reduce the number of possible actions especially whenV,Lor|Uj|is large.

With the decomposed action space, one of the branch in DDQN, i.e., the one estimating the advantage action functionabove Eq.(9), will be decomposed into 3 sub-branches.And each of them calculates the advantage action function for each subaction, such as(·) for actionaj,1.Hence, with dimension decomposition, Eq.(9) is replaced by theq-values for each dimension.That is, for thed-th dimension,

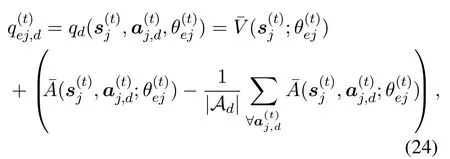
and

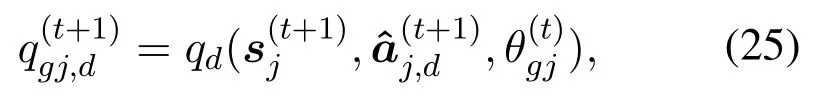
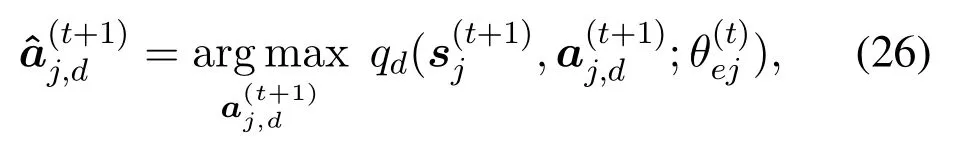
Meanwhile, in the aggregation node, the jointqvalue in Eq.(17)is calculated as

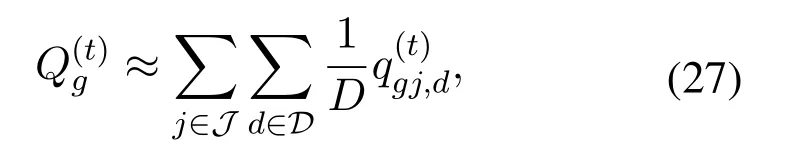
and Eq.(18)is also updated as

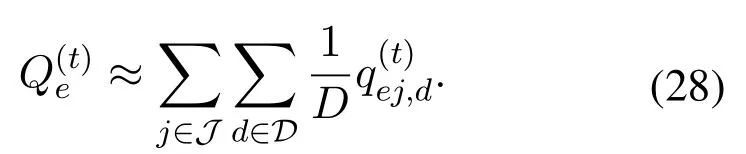
If one sub-action space in an independent dimension still brings the high computational complexity,we can further decompose this sub-action space to multiple sub-sub-action space.For instance,assuming that the decomposedAj,1is still relatively high in a specific caching scenario, we can further decompose theAj,1to multipleAj,1,d, and manage each sub-sub-action space by an independent neural network branch independently.In this way, the computational complexity can be further reduced.

We name the proposed dimension decompositionbased multi-agent deep reinforcement learning algorithm as value-decomposed dimensional network(VDDN).The detail steps are summarized in Algorithm 1.

VII.SIMULATION RESULTS

In this section, we test the performance of the proposed VDDN algorithm in the cooperative caching framework.The Zipf distribution is used to model the video popularity [39], while the uniform distribution is used to model the requested probability about quality versions.Furthermore, the VDDN algorithm was constructed using the PyTorch 1.5 and the detail parameters are summarized in Table 2.

Algorithm 1.Value-decomposed dimensional networks(VDDN)algorithm.Initialization:1: Initialize DDQN network for each agent with random parameters θej and θgj =θej,and the dimension number D for the action space.2: Initialize the parameters for reinforcement learning, including of explore probability ε, discount factor μ,learning rate ζ,reset step H,the gradient of loss function ∇y =0;Iteration:3: for time epoch t=1 to T do 4: for agent index j =1 to J do DDQN with Dimension Decomposition:5: Update θ(t+1)ej =θ(t)ej +ζ∇y(t).6: Every H steps,set θgj =θej.7: Observe state s(t)j from environment 8: for action dimension d=1 to D do 9: select a sub-action a(t)j,d ∈Aj,d with probability ε;or a(t)j,d =arg maxqd（s(t)）with probability 1-ε.10: calculate the q-values, q(t)a(t)j,d j ,a(t)j,d;θ(t)ej ej,d and q(t)gj,d according to(23)and(24).11: end for 12: Execute action a(t)j combined by all the subactions, then interact with the environment and receive the next state s(t+1)j j , s(t)j , q(t)ej,d, q(t)gj,d to the aggregation node.14: end for VDN in aggregation node:15: Observe a joint state S(t)and a joint action A(t),calculate the system reward r(t) according to(16).16: Store transition (S(t),A(t),r(t),S(t+1)) in experience replay library.17: Calculate the joint q-value Q(t)e and Q(t)g according to(26)and(27).18: Calculate the loss function y(t) and its gradient∇y(t)based on(19)and(20),respectively.19: Send ∇y(t)to each agent.20: end for 13: Send the information a(t)

7.1 Performance in Different Scenarios

In this subsection, we test the proposed VDDN algorithm with various scenarios,i.e.,different storage size in a BS and different file popularity distribution.

7.1.1 Impacts of BSs’Storage Sizes

In Figure 5, we plot the average rewards when each BS’s storage size,Z, varies.For simplification, the storage sizesZis set to 1～5 video layers.From the figure,it can be observed that:

· In all scenarios, the proposed VDDN algorithm converges.Since the reward value reflects the considered objective function, an obvious gain on system performance is achieved when storage sizeZincreases from 1 to 3.The performance gain fades away when further increasingZ, because the dominated popular file layers have been cached inside the cluster.

· Although the system performance improves with the increase ofZ, the time cost for convergence increases at the same time.Since the increase of storage size brings a larger action space in each agent, and a more larger joint action space, the agents in this cooperative framework take more time to seek the optimal policy.

7.1.2 Impacts of Video Popularity Distribution

In Figure 6, we show the average rewards when the different exponents are adopted in Zipf distribution,where a larger exponent implies a more uneven video popularity.It can be seen from the figure that

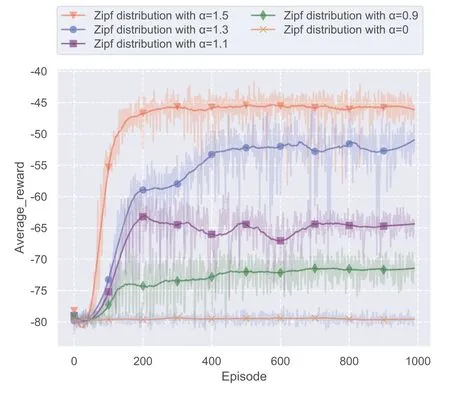
Figure 6.Impact of different parameter α in Zipf distribution.

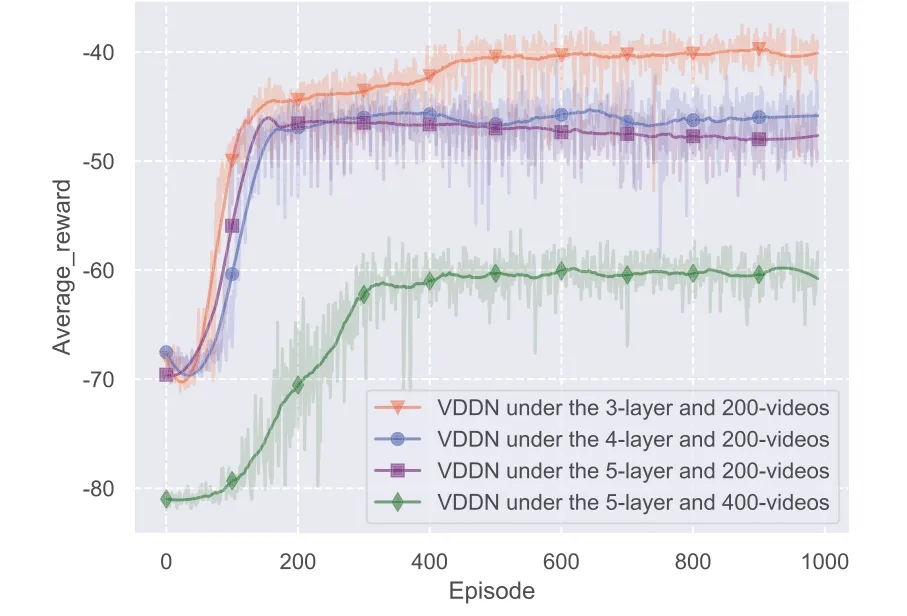
Figure 7.Impact of different video number and layer number.

· When video files have equal popularity with Zipf exponentα=0,caching any video file almost has the same performance, hence there is no reward increase during the training episodes.

· With the increase ofα, the average reward converges to a larger value, i.e., a better system performance.This performance gain comes from the less number of dominated video files.Caching these limited number of popular video can achieve a good enough performance.

· A larger Zipf exponent also leads to a quicker converge of the proposed algorithm.Since the users’ requests concentrate on few video files,the VDDN algorithm is more easier to find these video files.

7.1.3 Impacts of Weighting Coefficient

Since the proposed optimization problem aims at jointly optimizing the video access delay and the users’ MOS, a weighting coefficientηis introduced when we transform the multi-objective to a single objective, i.e., Eq.(4).Changing the value ofηreflects the weight of video access delay in the reward function of reinforcement learning.

From the results in Table 3,it can be seen that,with the increase ofη,the algorithm pays more attention to the performance of the video access delay.A largerηleads to a smaller video access delay, while a worseMOS.In more detail,ηincreases from 0.1 to 0.9,the average access delay for a user decreases almost 35%.In contrast, the average MOS decrease from 0.384 to 0.307.Also,whenηincreases larger than 0.7,the decrease of the average video access delay tends to be gentle, while there is still exist a large space for the increase of average MOS.

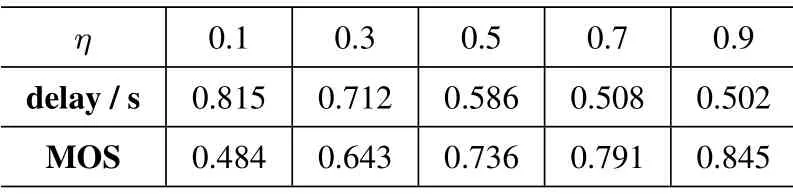
Table 3.Performance results per user in average delay and average MOS.

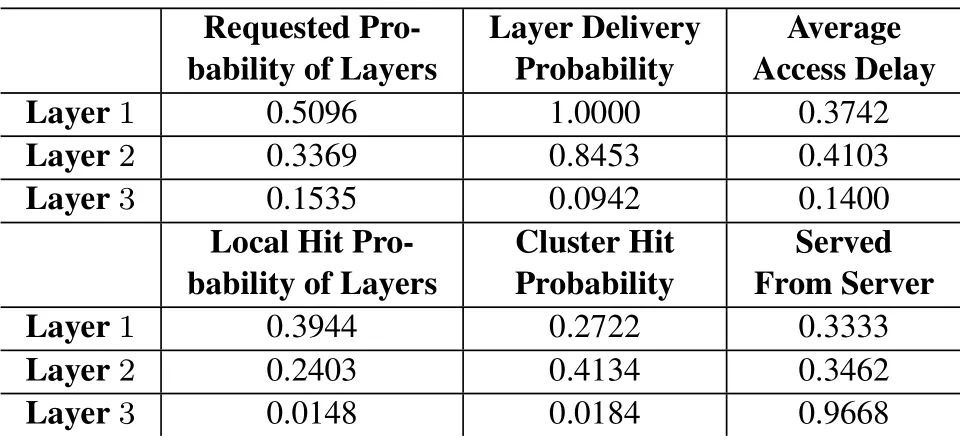
Table 4.Comparison among video layers in each episode.

7.1.4 Impacts of Video Parameters

In Figure 7, the training processes in four scenarios with different numbers of video filesVand layersLare simulated, from which we can see the proposed VDDN algorithm do deal with a large action space.Although the convergence for 400 videos and 5 layers is slower than the other three, only 300 episodes are needed.

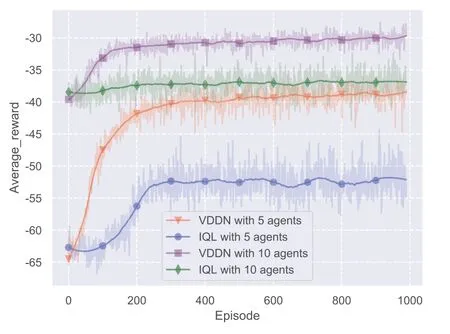
Figure 8.Comparison between IQL and proposed VDDN in different number of agents.

Also, we can see that given 200 videos, when the number of layers increases from 3 to 5, the average reward decreases a little due to the larger video quality range users may request.When we further increase the video library to 400 videos and 5 layers,more popular videos and more choices of video qualities result to the further decrease of the average reward.

7.1.5 Detail Performance in Different Video Layers From Table 4,it can be observed that given the distribution of users’requesting video quality,for instance,uniform distribution, the requested probability for a higher layer monotonically decreases.It is because in SVC, the higher layer works only when all the lower layers are completed,that is,to achieve a video qualityall the video layersl ≤are required.Due to the same reason,as seen from the table,the lower layers will always have the higher delivery probability.Hence, with limited storage size, the caching probability for a higher layer will be smaller as well as its cache hit probability.This phenomenon can also be observed in Table 4.

On the other hand,we can observe that the average access delay in each episode for Layer-3 is much less than Layer-2 and Layer-1.The reason for this phenomenon is that our algorithm may tend to degrade the video quality served for users aiming for a smaller video access delay, hence, Layer-3 is not delivered actually in many episode, as shown in the column -Layer Delivery Probability.The trade off between the video serving quality and the access delay is balanced by the algorithm.

7.2 Performance Comparison Among Different Algorithms

In this section, we compare the proposed algorithm with: 1)the traditional multi-agent DRL,named IQL in the following.That is, each agent employs an independent DDQN [40, 41], while there is no VDN deployed in the aggregation node and no dimension decomposition to reduce the action space; 2) traditional non-learning-based caching approaches including LRU,FIFO and random caching.

Note that, since IQL handle the complexity due to the large action space, a small number of videos is adopted.For an agent employed i7-8700 CPU and 16G RAM, the action space consisting of 20 video files, 5 video quality layers, 3 users and 5 storage spaces exceeds its memory capacity.In contrast,with the proposed VDDN algorithm, with dimension decomposition the action space into 3 sub-action spaces,this case can be easily handled.

7.2.1 Performance of Average System Reward

From Figure 8, it can be seen that in all scenarios tested, compared with the traditional IQL algorithm,the proposed VDDN algorithm achieves a better system performance, i.e., a higher average reward.In more detail, as shown in Figure 8, in the case with 5 agents, the VDDN algorithm improves the average reward by 27.1%, and in the case with 10 agents, the performance is enhance by 42.9%.The reason behind is clear,that is,the VDN in aggregation node provides a global observation and a overall system reward to each agent, which helps the agents to cooperate with each other and stride towards the global optimal.

In Figure 10,the two algorithm with different video numbers are tested.Compared the tradition MADRL,the proposed VDDN algorithm achieves a performance gain around 20% , in terms of the average reward, in the scenario with 5 videos and 5 video quality levels.And a larger performance gain is achieved in the scenario with 10 videos and 5 quality levels,almost 30%.Due to the enlargement of the action space,searching the global optimal action policy by each independent agent is more difficult.

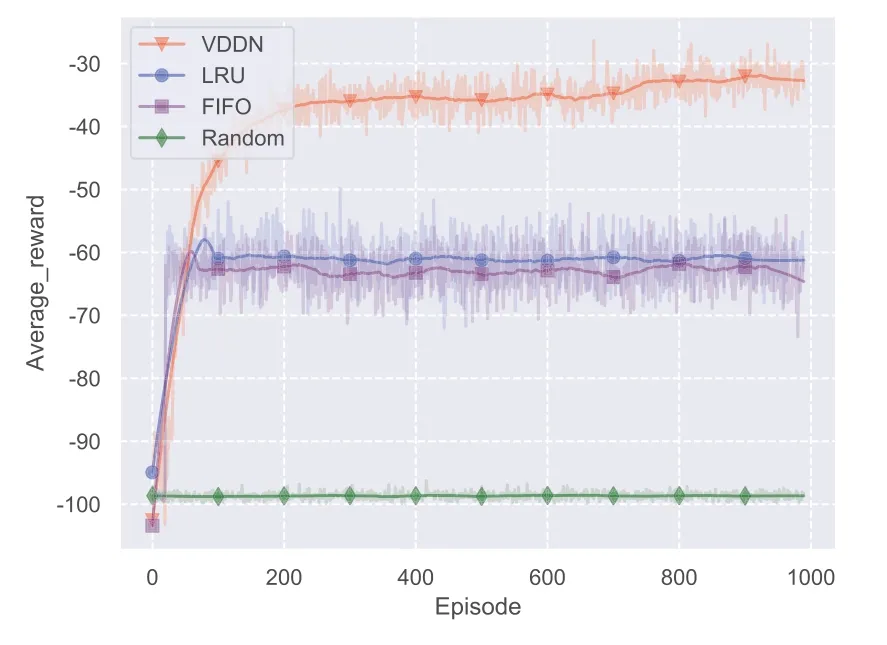
Figure 9.Comparison with traditional non-learning based algorithm.

Also, from the figure, compared with IQL, a quick convergence is another advantage of the proposed VDDN algorithm.Moreover, we can see an obvious oscillation during the training process when the IQL is adopted,which is a typical issue due to the influence of non-stationary environment[25].In contrast,the propose VDDN algorithm does not show this problem.

Additionally, we compare with the the proposed VDDN algorithm with three traditional non-learning algorithms: LRU, FIFO and random caching.From Figure 9, it can be observed that, the proposed VDDN algorithm outperforms these algorithms.Explicitly, the performance gain of VDDN compared with LRU, FIFO and random caching are 71.4%,77.1% and 183%, respectively.The reason behind is that learning-based methods can better capture the file preferences of the users based on the training process.

7.2.2 Performance of Training Time

As mentioned before,the traditional MADRL can not handle a very large action space due to the limited memory.For instance,we compared the performance of training time in some specific situations.In Figure 11,we compare the training time of the two algorithms.It can be seen that,given the action space with 5 videos, the average training time spent per training episodes is 3.51s when adopting IQL,while it is only 2.53s when adopting the proposed VDDN.That is,in the small action space cases, the proposed VDDN algorithm improves the training speed by 28%.When the number of videos increases to 10 videos, the average training time of IQL has been significantly increased to 5.43s,while the training time of VDDN has only increased 0.32s in one episode.

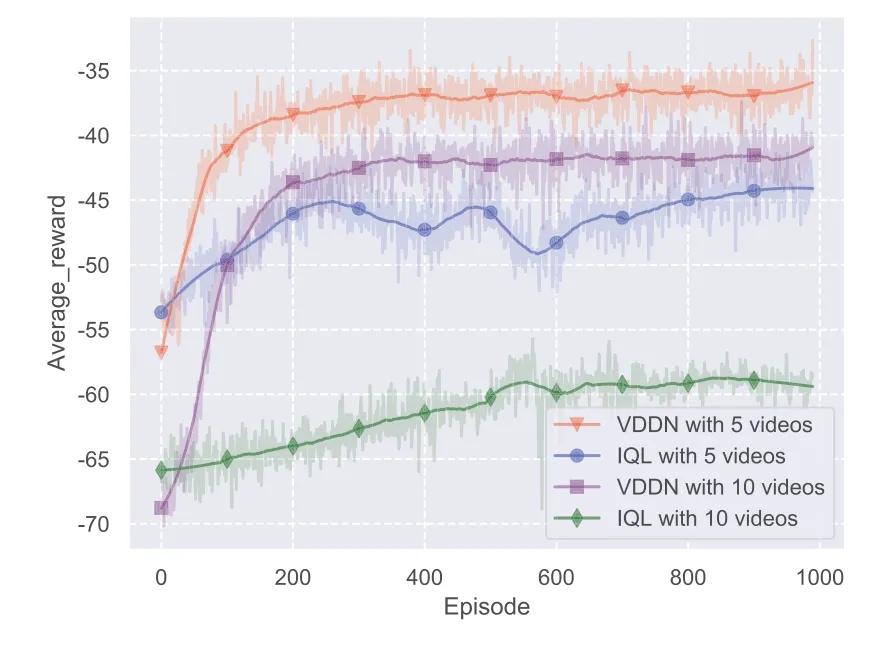
Figure 10.Comparison between IQL and proposed VDDN with different number of videos.

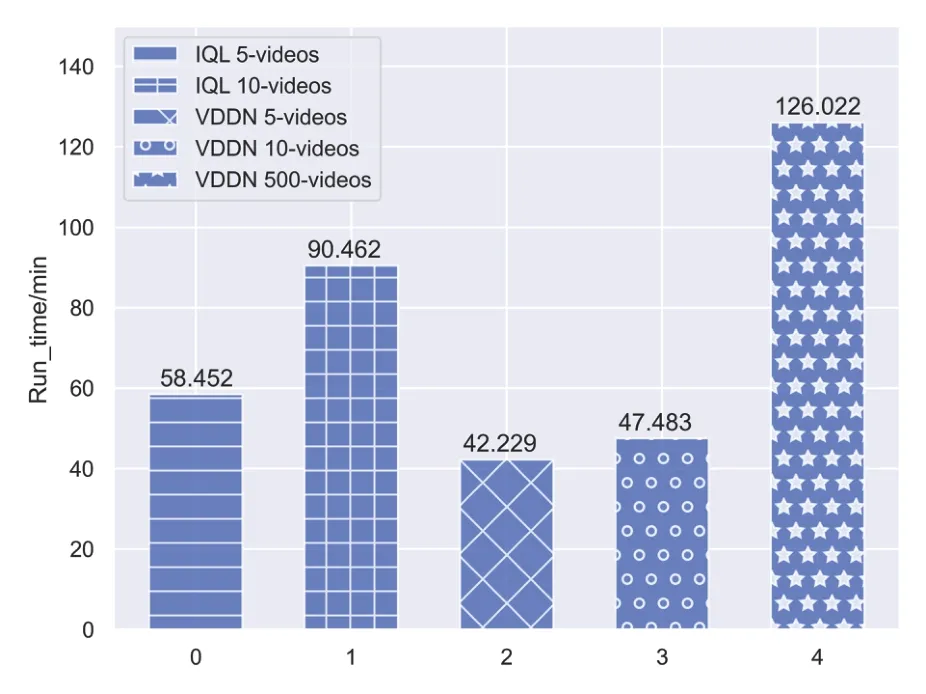
Figure 11.Training time comparison between IQL and proposed VDDN in different number of videos.

Figure 11 shows the training time spent by VDDN with 500 videos,it can be seen that the training time of the proposed VDDN does not increase exponentially with the computational complexity as the action space.The computational complexity as well as the training time is still in an acceptable range under such complex scenario.Hence, we can conclude that the computational complexity in each agent is greatly reduced with dimension decomposition.

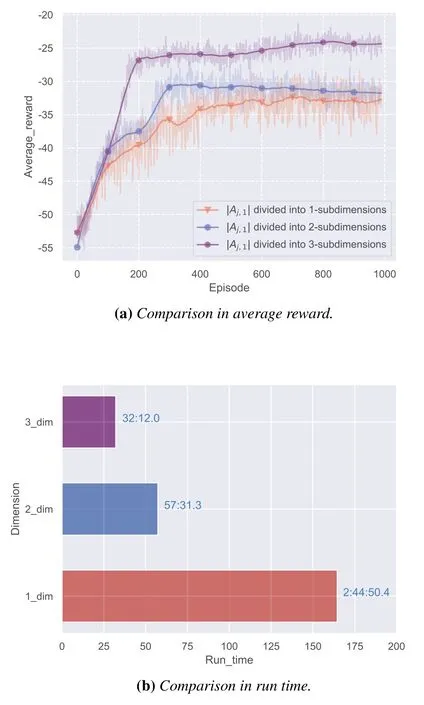
Figure 12.Comparison in different number of subdimensions in Aj,1.

7.3 Performance of Dimension Decomposition

The number of dimensionsDadopted in the dimension decomposition undoubtedly affects the performance of our algorithm,for example,when the storage sizeZ= 6 and video numberV= 200, the size of sub-action space|Aj,1|about the video selection still has a higher computational complexity.Here,we can further decompose the sub-action space|Aj,1|to manage the video selection of the storage with multiple network branches,each branch manages the selection of a part of storage space.

Figure 12 depicts the results about the system reward and training time of the our framework.When the sub-action space|Aj,1|is further divided into different number of sub-dimensions, the following phenomena can be seen,

· when the number of sub-dimensions increases,the VDDN algorithm not only achieves a higher system reward, but also makes training process more smoothly.Meanwhile, larger number of sub-sub action spaces contributes to a faster convergence as shown in Figure 12(a).It suggests that increasing the number of action spaces help the agents to a faster and more stable action spaces.

· Increasing the number of sub-sub-action spaces reduces the training time.As illustrated in Figure 12(b), the training time for 2-subdimensions and 3-subdimensions inAj,1is reduced by 65.1%and 80.5%,respectively,compared to the original 1 sub-action space.

VIII.CONCLUSION

In this paper, we optimized the video-layer caching and video-quality service strategies in a cluster-based wireless caching system with SVC.A VDDN algorithm was proposed to simultaneously minimize the video access delay and maximize the user’s satisfaction, in terms of MOS.Compared with traditional MADRL consisting of independent agents, the proposed algorithm introduced a VDN employed aggregation node, which achieved an obvious performance gain due to the global observation and overall system reward obtained.Meanwhile, to deal with the high memory cost and computational complexity due to an extreme large action space in the context of SVC,the dimension decomposition was adopted to break down a large action space into multiple independent sub-action spaces.Experimental results showed that the proposed algorithm can handle a much larger network and video libraries, and the training time spent was also much less, compared with the traditional MADRL.

ACKNOWLEDGMENTS

This work was supported by the National Natural Science Foundation of China under Grant No.61801119.