非齐次树上马氏链基于韦伯分布的一个强偏差定理

任双双 兰晓博

(郑州科技学院基础部 河南郑州 450064)

近年来，许多学者对树指标随机过程的研究至今方兴未艾，其中关于强偏差定理的研究也一直颇受青睐。文献[1]主要研究并给出了马氏环境中关于齐次树指标的马氏链的渐进均分性，文献[2]研究并给出了树指标马氏链关于广义几何分布的一个强偏差定理，文献[3]给出了关于树指标非齐次马氏链的广义熵遍历定理。该文通过引入滑动相对熵的概念，构造适当的tn(λ,ω)，将Doob鞅收敛定理和上、下极限性质应用到定理中，研究并给出了关于韦伯分布的强偏差定理,使该方面的内容得到了扩充。

1 基本概念

定义1 定义{Xσ,σ∈T}是概率空间{Ω,F,P}上，且在连续状态(R+,β(R+))取值的随机变量族，设

是随机变量族{Xσ,σ∈T}的初始分布，且正则条件概率族[4]记为

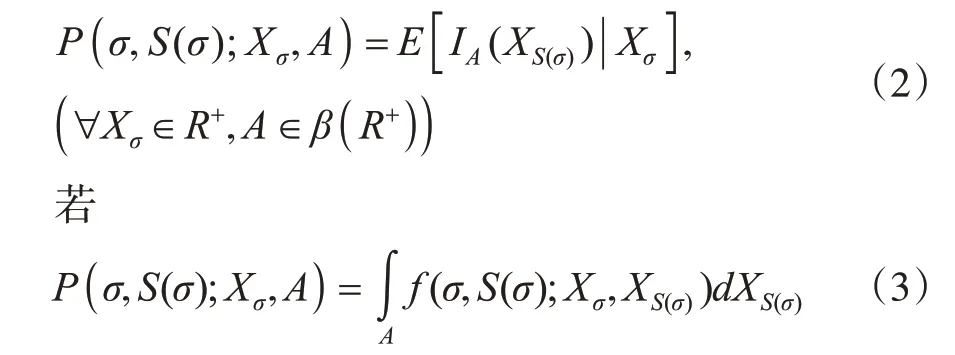
则称f(σ,S(σ);Xσ,XS(σ))为转移密度函数，记

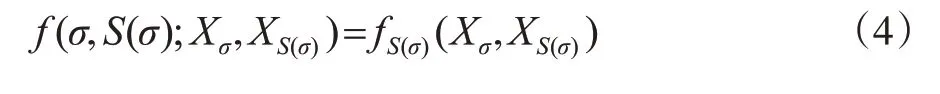
定义fS(σ)(Xσ,XS(σ))是初始分布{Xσ,σ∈T}的一列转移密度函数，将f0定义为{Xσ,σ∈T}对应的概率密度函数，于是称为具有式（1）和式（2）的在R+上取值的连续状态树指标非齐次Markov链[5]。

则定义的树T上联合分布密度函数[6]为

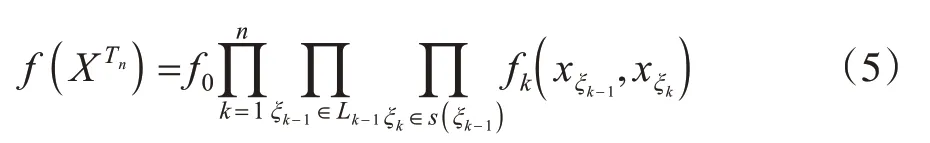
设(Ω,F)上的另一概率测度为Q，{Xσ,σ∈T}在Q下的联合分布密度函数记为

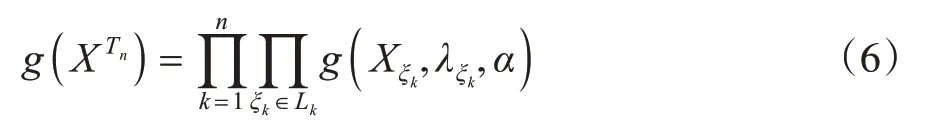
也就是{Xσ,σ∈T}在Q下互相独立，并且服从的韦伯分布，其中,λξk＞0,α＞0,xξk∈R+,ξk∈Lk。

定义2{Xσ,σ∈T}在P和Q下的联合分布密度函数均如上式所定义，设0 ≤a1≤a2≤…是一列整数值，分别记

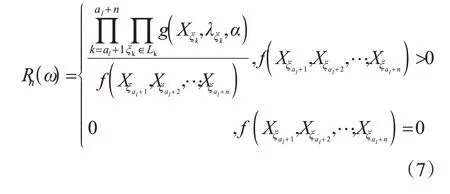
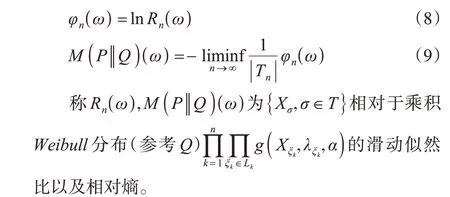
定义3 设f(x)是随机变量X的密度函数,如果存在0 ＜δ＜1使

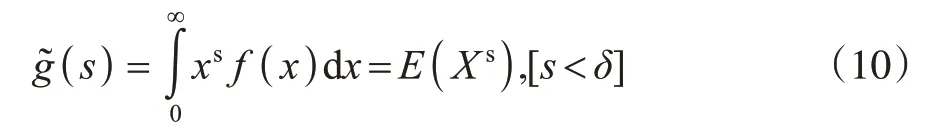
存在，则称(s)是随机变量X的s-矩变换。

由式（10）知，对于服从分布g(xξk,λξk)的随机变量Xξk的s-矩变换为

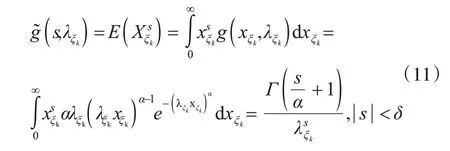
2 强偏差性质

引理1 设{Xσ,σ∈T}为如上定义的连续状态树指标非齐次Markov 链，其中0 ≤a1≤a2≤…是一列整数值，s为一实数，f(X Tn)，g(X Tn)，(s,λξk)如前定义，令

则{tn(s,ω),σ(Xξal+1,Xξal+2,…,Xξal+n),n≥1}在概率测度P下是一非负鞅。

证明由式（5），有

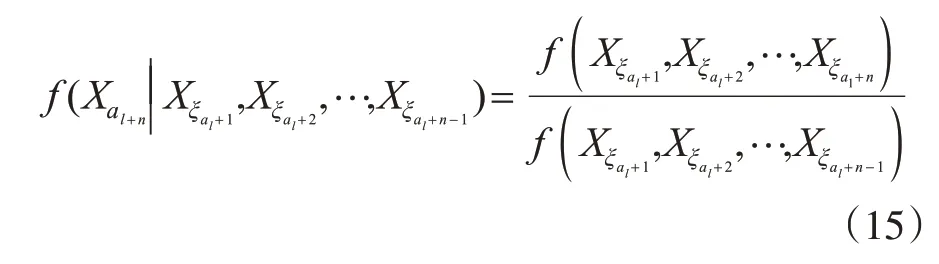
由式（11）、式（12）、式（13）与式（14），有

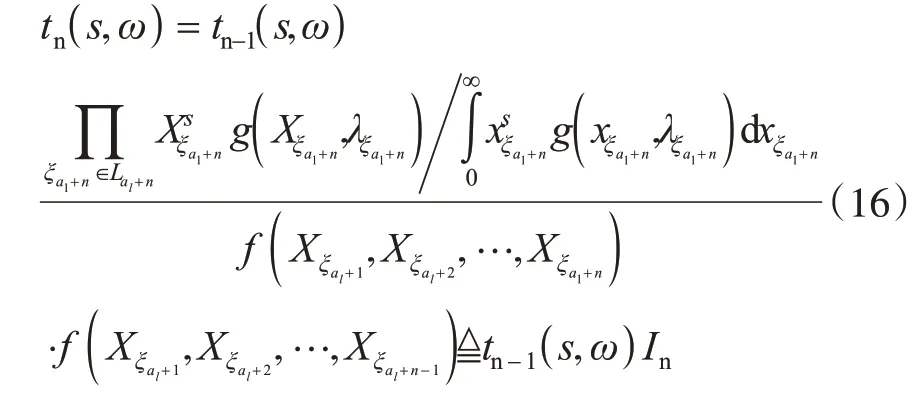
由式（15）与式（16），有

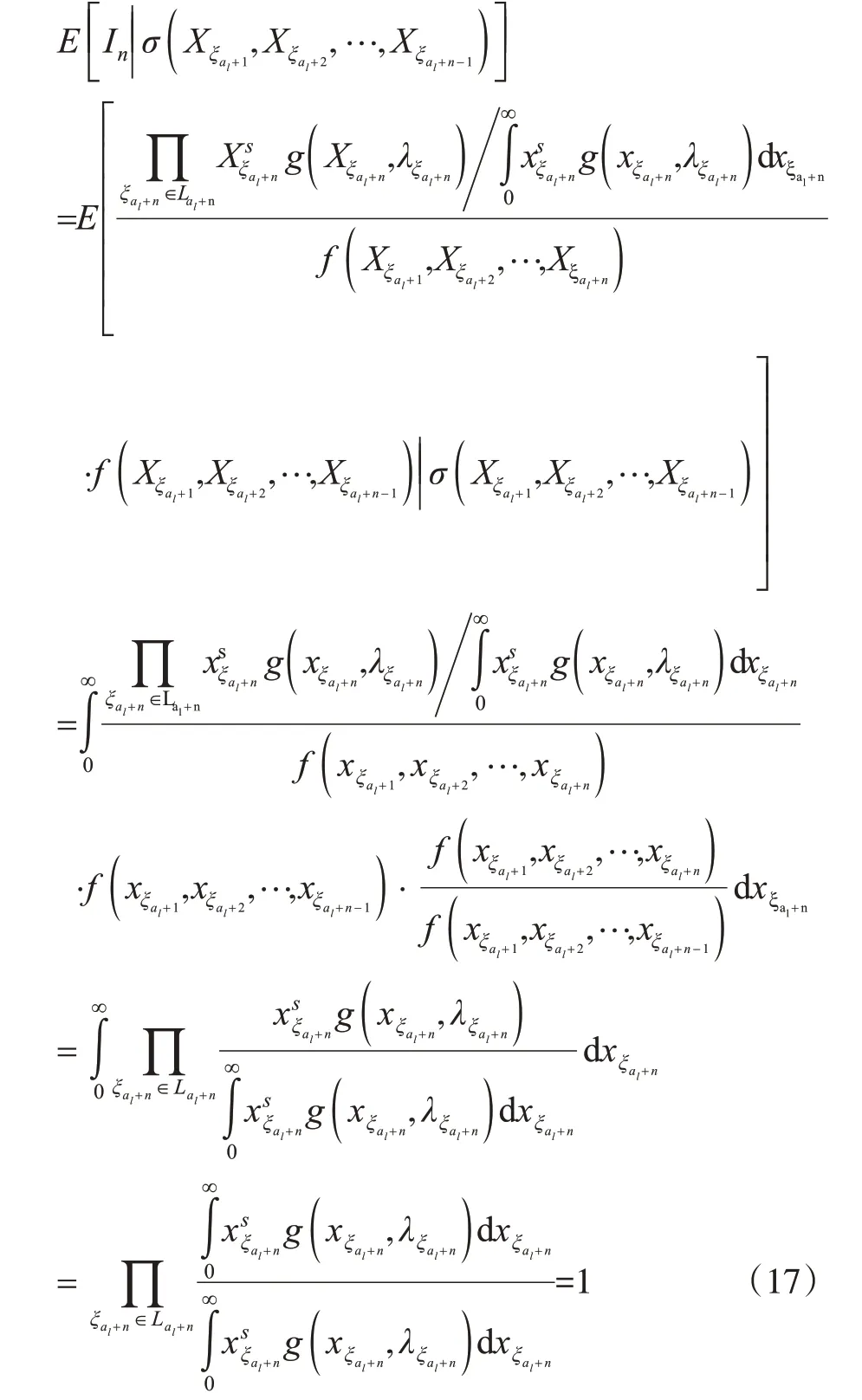
由（16）式和（17）式，有

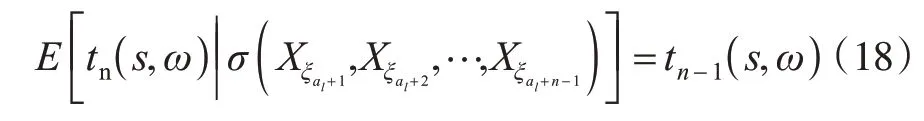
则{tn(s,ω),σ(Xξal+1,Xξal+2,…,Xξal+n),n≥1}在概率测度P下是一非负鞅[7]。

定理1 设{Xσ,σ∈T}为如上述定义的连续状态树指标非齐次Markov链，其在Q下的联合分布密度函数如式（6）所定义，实数s∈(-1,1)，正整值数列{al,l≥1}如前定义。设存在M＞0，使得

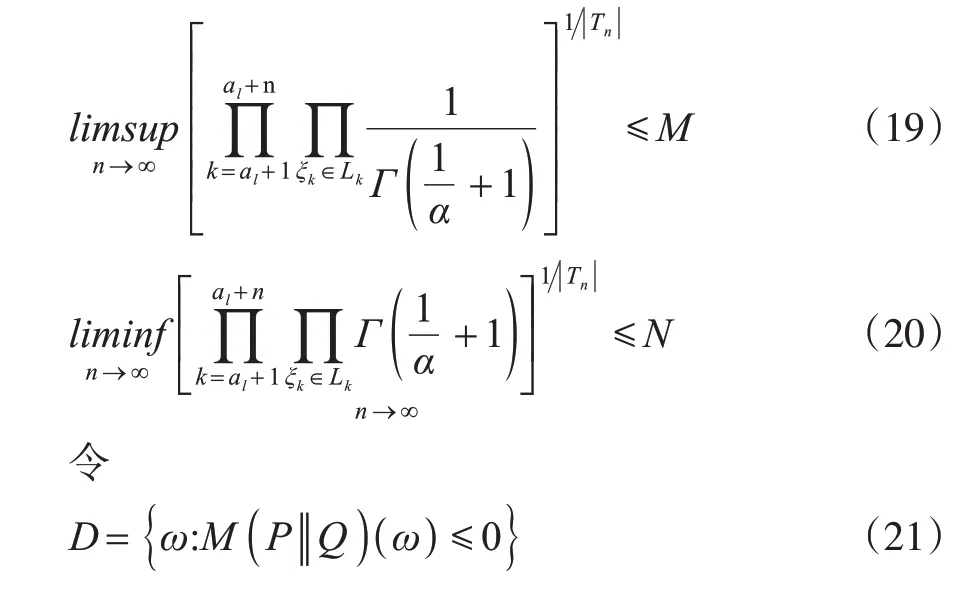
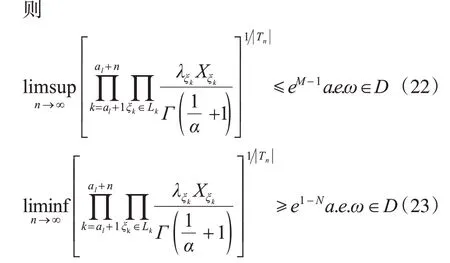
证明 由引理1 及Doob 鞅收敛定理[8]知，存在A(s) ∈F，P(A(s))=1，使得

由式（7）、式（11）、式（12）、式（13）与式（14），有

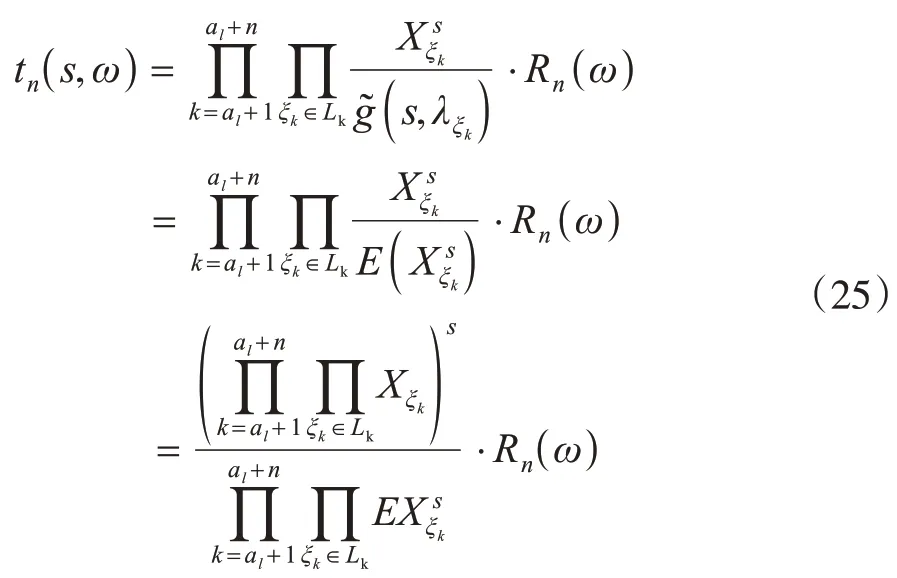
由（25）式，有

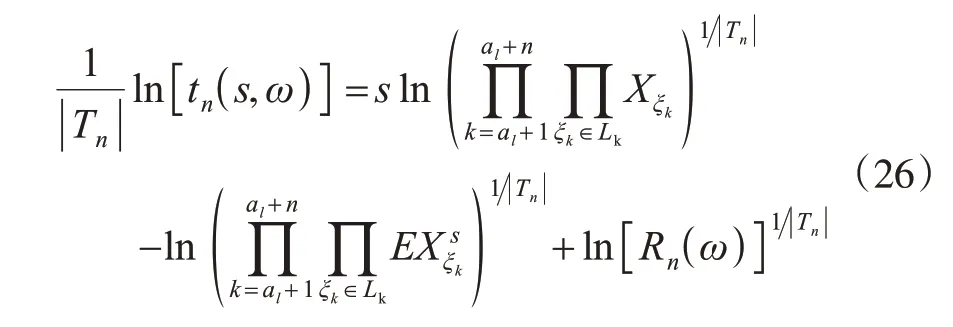
由式（8）、式（9）、式（21）、式（24）及式（26），有

取0 ＜s＜1，将（27）式两端同除以s，有

由不等式lnx≤x-1(x＞0)及式（11）、式（19）、式（29）可知

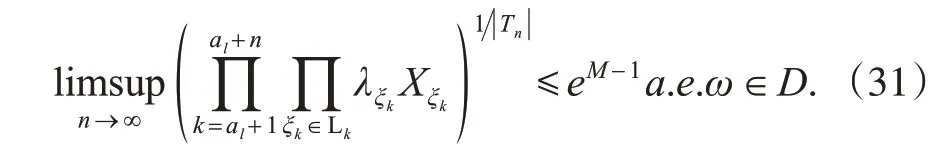
由式（31），有式（22）成立。

取-1 ＜s＜0，将式（27）两端同除以s，有

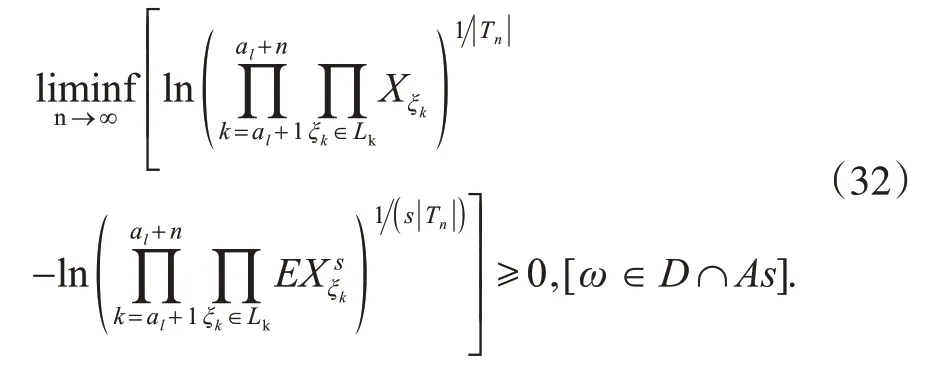
由式（32）及下极限的性质

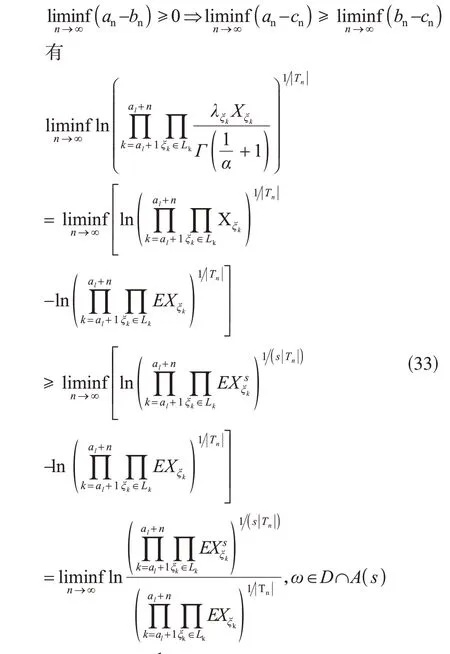
由式（35），有式（23）成立。