基于广义框架的概率认知逻辑

2022-09-15 10:27邓美林郭美云

逻辑学研究 2022年4期

邓美林郭美云

1 引言

概率认知逻辑最早由费金（R.Fagin）和哈尔彭（J.Y.Halpern）在[7]中提出，他们将概率公理结合到认知逻辑中，提出了概率认知逻辑的公理化系统，讨论了完全性，可判定性和模型的一些特殊性质。巴尔塔格（A.Baltag）、范·本特姆（J.van Benthem）、库伊（B.P.Kooi）等人分别在[2,3,9]中推进了概率认知逻辑在概率认知动态化方面的研究，并提出了另一种概率指派方法。概率认知逻辑语义模型可以据其关于概率指派的不同方法概括为两种1这两类模型分别对应于由德米（L.Demey）和萨科（J.Sack）在文献[5]中提出的probabilistic relational model和simplified probabilistic relational model。：将概率函数建立在概率空间上的概率空间认知模型，文献[1,5,7,11]采用了这种方法；将概率函数建立在每一个可能世界上的离散概率认知模型，文献[2,3,5,9]采用了这种方法。

采用概率空间认知模型的做法无法保证所有公式都被指派概率。因而如果所有给定的命题都有概率，概率空间认知模型就不能恰当地刻画这种情形下的概率推理。为了让模型能够为给定语言中的所有公式指派概率，文献[7]定义了一个关于原子命题和三个关于概率函数的特殊性质2参考文献[7]的引理3.1，其中的四个特殊性质分别为PMEAS，CONS，OBJ 和UNIF。，前者使得所有命题逻辑公式是可测的，后者使得认知逻辑公式和概率公式是可测的。但是就模型的可测问题而言，这一方案中的限定过强了。文献[5]注意到广义框架中可允许赋值集与σ代数3集合X 的σ 代数是一个包含X，对补运算和可数并运算封闭的X 的子集的集合。的共通点，并据这一共通点提供了一个更好的方案。但是为了解决概率公式的可测问题，这一方案给出的定义过于繁琐，模型构造的可操作性不强。离散概率认知模型为每个可能世界指派概率，因而不存在概率公式的可测问题。但离散概率认知模型不能在可数无穷多个世界的情形下为所有世界指派相等的概率。4假设可能世界集是可数无穷的，令主体i 在世界w 上给每个可能世界指派概率为而这与这一要求相矛盾。

文献[4]给出的广义框架中关于可允许赋值集的定义与概率空间中的σ代数的定义相似。广义框架的英文表述为general frame，可允许赋值集的英文表述为set of admissible valuations。可允许赋值集对运算封闭性的要求在一定程度上可以解决[7]指出的公式不可测问题，同时它又能解决离散概率认知模型面临的问题。因此，我们尝试用广义框架代替普通框架，并将概率指派到可允许赋值集上。我们给出了一个可靠且完全的概率认知逻辑公理系统并表明这一逻辑适用于谈论混合策略博弈。

本节以后的内容安排如下：第二节介绍基于广义框架的概率认知逻辑的语言、语义和公理系统PELG（Probabilistic Epistemic Logic based on General frame），并通过模型比较，明确了基于广义框架的概率认知模型的优势；第三节证明PELG的可靠性和完全性；第四节运用基于广义框架的概率认知模型刻画混合策略博弈的两种状态；第五节总结本文的主要工作和一些有待研究的问题。

2 基于广义框架的概率认知逻辑PELG

2.1 PELG 语言

定义2.1(形式语言LPELG).令At表示原子命题集，Ag表示有穷主体集，概率认知逻辑公式LPELG定义如下。

其中，a1,...,an和b是任意有理数，a1Pi(φ1)+a2Pi(φ2)+···+anPi(φn)≥b是基本概率公式，表示主体关于φ1,...,φn的概率。据定义，Pi(φ)≥b是概率公式，表示在主体i看来，φ的概率大于等于b。Pi(φ1)≥Pi(φ2)也是概率公式，表示在主体i看来，φ1的概率大于等于φ2的概率。我们称为项，记为t，当括号在公式最外层时，通常略去不写。

如下LPELG公式都可通过以上公式得到定义：φ →ψ，φ ∧ψ，φ ↔ψ，⊤，⊥，

2.2 基于广义框架的概率认知模型

定义2.2(模型).给定有穷主体集Ag和命题逻辑原子公式集At，一个基于广义框架的概率认知模型M=〈W,Ri,A,µ,V 〉i∈Ag，其中W是非空的可能世界集，Ri是主体i的认知可及关系（等价关系），A⊆℘(W)是可允许赋值集，即A 是非空集且满足：

1.X ∈A⇒WX ∈A；

2.X1,X2,...∈A⇒5此处定义的可允许赋值集对可数并运算封闭，是对广义框架中的有穷并运算封闭条件的推广，广义框架的定义可参见文献[4]第29 页。如果一个集合对可数并运算封闭，那么它一定对有穷并运算封闭。

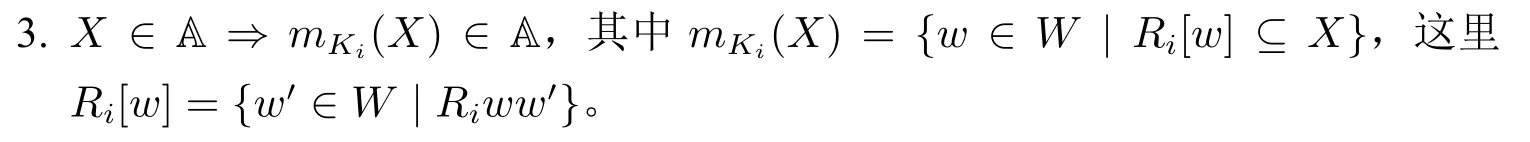
V:At →A 是命题逻辑原子公式赋值函数，我们称之为可允许赋值，µ:Ag×W →(A→[0,1])是概率函数，为每一个主体i在每个世界w上给A 中的每个世界集指派一个0 到1 区间上的有理数，使得

〈W,Ri,A,µ〉i∈Ag是一个概率认知广义框架，记为F，我们称〈W,A〉是一个可测空间，称〈W,A,µ〉是一个测度空间。在以下行文中，在不引起混淆的情况下，概率认知模型都是指基于广义框架的概率认知模型。

关于可允许赋值集A 的三个条件分别表明，可允许赋值集关于补运算、并运算、模态运算封闭。概率函数的前两个条件是对概率的一般性要求。概率函数的第三个条件表明，如果对于任意W的子集W′，任意X ∈A 和任意w,u ∈W′，都有µi,w(X)=µi,u(X)，那么，W′ ∈A。6如果对于任意w,u ∈W′，都有µi,w(X)= µi,u(X)，那么，对于任意当且仅当因此，据概率函数的第三个条件，{w ∈W | w ∈W′} ∈A，即W′ ∈A。换言之，可允许赋值集关于概率运算也是封闭的。

定义2.3(语义).给定概率认知模型对于任意世界w ∈W，LPELG公式在点模型(M,w)上为真记为M,w |=φ，定义如下。

• M,w |=p当且仅当w ∈V(p)；

• M,w |=¬φ当且仅当

• M,w |=φ ∨ψ当且仅当M,w |=φ或M,w |=ψ；

• M,w |=Kiφ当且仅当对于任意w′ ∈W，如果Rww′，那么M,w′ |=φ；

• M,w当且仅当

定义2.4(可测).给定概率认知模型M，令表示公式φ的外延，一个LPELG公式φ在M 中是可测的当且仅当

定理2.1.所有LPELG-公式在概率认知模型中都是可测的。

对LPELG公式的结构进行归纳易证定理2.1。概率认知模型定义表明，可允许赋值集关于补运算、并运算、模态运算的封闭性要求，分别对应于公式的否定、公式的合取以及公式的模态。命题逻辑原子公式赋值函数保证了所有给定的命题逻辑原子公式的外延都在可允许赋值集中。再据以上封闭性条件，可得所有据给定的命题逻辑原子公式生成的LPELG认知公式（不含概率公式）的外延都在可允许赋值集中。

可允许赋值集同时也是σ代数，由可能世界集、可允许赋值集和概率函数组成一个概率测度空间〈W,A,µ〉。概率函数为σ代数即可允许赋值集中的每一个元素指派概率。因此，所有给定的LPELG认知公式的外延都被指派了概率。再据概率函数的第三个条件可知，所有LPELG概率公式的外延也都在可允许赋值集中，这使得所有LPELG公式的外延都被指派了概率，据定义2.4 可知，所有LPELG公式都是可测的。因而定义2.3 是良定义的。

[5]提出了一个广义σ代数7即general σ algebra，参考文献[5]定义4.6。，但没有明确地定义出基于广义框架的概率认知模型。据命题2.2 可知，这一方案所定义的模型等价于本文定义的概率认知模型。相对而言，本文定义的概率认知模型更为简洁、易于构造。此外，基于广义框架的概率认知模型由于保留了概率空间的性质而能够在可能世界集是可数无穷的情况下为不同的世界子集指派均等概率。

需要指出，本文没有对模型中的广义框架做具体限定，且普通框架8普通框架指的是〈W,R〉，当可允许赋值集A= ℘(W)时，〈W,R,A〉就是一个普通框架。是广义框架的特例。在本文的基础上，可以定义一类具有某些特性的广义框架，从而扩充概率认知逻辑公理系统。[4]主要从可允许赋值集的角度定义了几类广义框架（第30、第308 页），比如限定可允许赋值集包含所有有穷集和余有穷集（co finite）、令可允许赋值集是可区分的（differentiated）等等。此外，还可以定义一些特殊的概率函数，进而讨论知识与概率、信念与概率的互动关系。9为了刻画某种知识与概率的互动，可以对概率函数作如下要求：对于任意X ∈A，Ri[w] ⊆X，当且仅当µi,w(X)=1，可以称这一性质为“知识概率一致性”。

2.3 模型的比较

[5] 比较了概率模型和离散概率模型，并指出离散概率模型是概率模型的特例。令M=〈W,ν,V〉是一个离散概率模型,其中ν是一个概率函数，在每个世界上为每个世界指派一个概率。令{ν+(X)=∑x∈X ν(x)| X ∈℘(W)}，那么M+=〈W,℘(W),ν+,V〉是一个由离散概率模型M 生成的概率模型。10关于概率模型与离散概率模型、概率空间认知模型和离散概率认知模型的关系的详细讨论参考文献[5]第4.2.1节和4.5.1 节。同理可得，离散概率认知模型是概率空间认知模型的特例。本文定义的概率认知模型是第三种模型，因此有必要讨论一下三者的关系，本文从模型等价的角度展开讨论。

定义2.5.任给概率认知模型M 和M′，M 和M′是LPELG等价的，若对于任意LPELG公式φ，M|=φ当且仅当M′ |=φ，记为M ↭M′。

离散概率认知模型的概率指派和概率运算都比较简单。[9]最早定义了离散概率认知模型，用以讨论概率动态认知逻辑。11在动态的概率认知逻辑中通常都采用这一模型，[9]运用这一模型讨论了三门问题12，[2]运用这一模型讨论了信息瀑布（informational cascade）。信息瀑布的详细讨论参考文献[2]第3 节。由于离散概率认知模型的定义相对简单，本文只给出离散概率认知模型与基于广义框架的概率认知模型的一个比较结果，有兴趣的读者可参考文献[3]的定义1、[5]的定义4.4 和[9]的定义1。事实上，离散概率认知模型是基于广义框架的概率认知模型的一个特例，当可允许赋值集A=℘(W)时，这样的基于广义框架的概率认知模型就等价于一个离散概率认知模型。

在概率认知模型中，我们将概率指派给可允许赋值集中的元素，而不再为每一世界构造一个概率空间，但是每个世界上的概率指派却可以是不同的。也就是说，我们预设主体在每一个可能世界上都有一个相同的可测空间，但并不预设主体在每一个可能世界上具有相同的测度空间。因此，概率空间认知模型在每个世界上建立一个概率空间的要求实质上可以通过概率指派来实现。我们通过命题2.2 表明，如果所有给定命题的概率都是可测的，那么采用基于广义框架的概率认知模型来定义语义更为简洁，而这一模型与概率空间认知模型具有同等的刻画能力。

定义2.6(概率空间认知模型).给定有穷主体集Ag和命题逻辑原子公式集At，概率空间认知模型Mu是一个四元组〈W,Ri,P,V〉i∈Ag，其中W是非空的可能世界集，Ri是主体i的认知可及关系（等价关系），V:At →℘(W)是命题逻辑原子公式赋值函数，Pi,w=〈Si,w,Ai,w,ξi,w〉是概率空间，其中：

•Si,w ⊆W是主体i在世界w上的样本空间；

•Ai,w是Si,w上的σ代数；

定义2.7.概率空间认知模型Mu具有可测性当且仅当存在℘(W)上的σ代数A，使得V:At →A，并且对于任意i ∈Ag，任意w ∈W，

概率空间认知模型的可测性定义最早出现在[5]的定义4.6，[5]定义的广义σ代数A只能保证命题逻辑公式和认知逻辑公式是可测的，为了使得概率公式在模型中是可测的，[5]对概率空间Pi,w做了限定。与此不同，定义2.7 将类似的限定增加到广义σ代数的定义中。

命题2.1.所有LPELG-公式在具有可测性的概率空间认知模型中都是可测的。

概率空间认知模型要求在每一个可能世界上为每一个主体构造一个概率空间Pi,w，相应地，概率公式的语义定义要求为公式φ的外延与一个样本空间Si,w构成的交集指派概率。在基于广义框架的概率认知模型中，概率指派针对的是可允许赋值集中的元素，因而不用考虑不同的概率空间问题，概率被指派给每个公式的外延，而不用再求交集。并且，命题2.2 表明，如果给定命题的概率都是可测的，那么基于广义框架的概率认知模型与概率空间认知模型具有同等的刻画能力。

2.4 PELG 公理系统

定义2.8 (PELG 公理系统).PELG 是一个包含如下公理模式和变形规则的证明系统。

Taut所有经典命题逻辑重言式例示

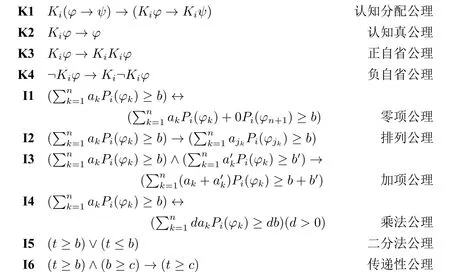
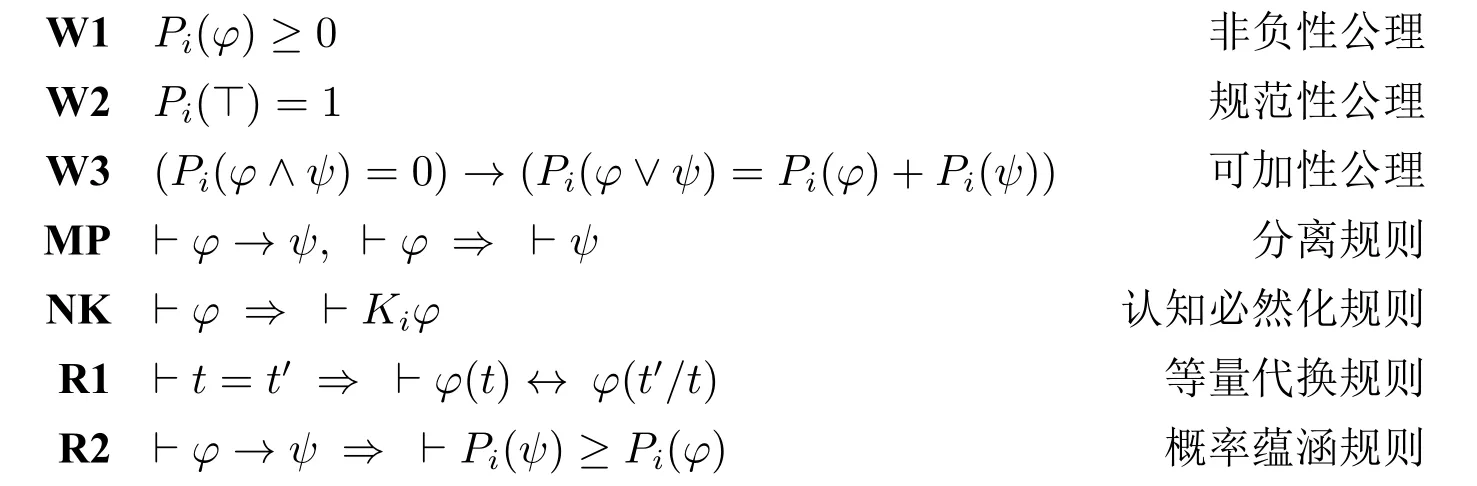
本文用⊢PELGφ表示φ在PELG 中是可演绎的，也称φ是PELG 的定理。PELG中φ的一个演绎指的是一个有穷长度的公式序列，序列最后的公式是φ，序列中的任一公式或者是PELG 的公理，或者是运用PELG 的某一规则从序列中前面的公式得到的。在不引起混淆的情况下，我们都用⊢表示⊢PELG。

易证如下命题：

命题2.3.PELG 定理和导出规则：

1.Pi(⊥)=0；

2.Pi(¬φ)=1-Pi(φ)；

3.⊢φ ↔ψ ⇒ ⊢Pi(φ)=Pi(ψ)。

3 可靠性和完全性

定理3.1(可靠性).对于任意LPELG-公式φ，⊢φ ⇒ |=φ。

据语义定义，可证所有PELG 公理在任意概率认知模型M 中是有效的，所有PELG 规则在概率认知模型M 中保持有效性。13一个规则保持有效性当且仅当据这一规则从有效式只能推出有效式。可参考[6–8]中的相关证明，由于篇幅所限，这里略去证明。

定义3.1(闭包).任给LPELG公式φ，φ的闭包cl(φ)指的是使得φ ∈cl(φ)且满足如下条件的最小公式集：

• 如果ψ ∈cl(φ)，那么Sub(ψ)∈cl(φ)；14Sub(φ)表示φ 的所有子公式的集合。

• 如果ψ ∈cl(φ)并且ψ不是一个形如¬φ的公式，那么¬ψ ∈cl(φ)。

定义3.2(Φ的极大一致集).令Φ为某LPELG公式的闭包，Γ是Φ的极大一致集当且仅当且如果Γ′ ⊆Φ且Γ⊂Γ′，那么Γ′ ⊢⊥。

将典范模型限制在公式的闭包上，是因为公式闭包中的公式是有穷多的。引理3.2 表明，对于任意有穷且一致的公式集，一定存在满足典范要求的概率函数。然而，针对一个无穷且一致的公式集，可能不存在这样的概率函数。比如，没有概率函数能够满足公式集{Pi(p)<1}∪{Pi(p)≥r |r <1}。由此可知，PELG 相对于概率认知模型没有紧致性，进而PELG 没有强完全性。

引理3.3(典范性).令Φ 是某LPELG-公式的闭包，Φ 的典范模型Mc是一个概率认知模型。

证明.易证是等价关系，据典范模型定义，µc是一个概率函数，据引理3.2，满足典范要求的µc是存在的，其余显然满足概率认知模型定义。

引理3.4(真值引理).令Φ 为某LPELG-公式的闭包，令是Φ 的典范模型。对于任意wc ∈Wc，任意公式φ ∈Φ：φ ∈wc当且仅当

[7]提出了一种证明概率认知逻辑完全性的方法，这一方法的核心思想仍然是构造一个真值引理，使得任意概率认知逻辑公式在一个极大一致集中当且仅当这一公式在这一极大一致集上可满足。在[7]的基础上，我们定义了一个典范的概率认知模型，命题3.1.8 表明，对于满足一定条件的概率公式，我们可以将这一公式的概率分配到闭包中的所有极大一致集上。而在真值引理的证明中，我们根据零项公理将这一结论推广到任意概率公式。进而根据概率公式在极大一致集中出现与否，典范的概率函数为闭包中的所有极大一致集指派概率，闭包中的任意概率公式就与典范的概率函数联系了起来。为了证明典范的概率函数是存在的，我们提出并证明了概率函数存在引理，同时表明典范概率认知模型是良定义的。

定理3.2 (弱完全性).概率认知逻辑PELG 相对于概率认知广义框架类是弱完全的：对于任意LPELG-公式

证明.任给LPELG公式φ，令那么{¬φ}是一致的，令Φ 为{¬φ}的闭包，据林登鲍姆引理，{¬φ}是Φ 的某个极大一致集Γ 的子集，再据真值引理，存在Φ 的典范模型Mc，使得据引理3.3，Mc是一个概率认知模型，因此，

4 应用

在一些策略式博弈中，没有纯策略纳什均衡或有多个纯策略纳什均衡，但存在唯一的混合策略纳什均衡。我们用概率认知逻辑为如下协同博弈（Coordination Game）的混合策略提供一个逻辑解释。

例1(协同博弈).一对情侣打算安排他们的娱乐活动，或者听音乐会，或者看电影。女士偏好音乐会，男士偏好电影，但他们都宁愿在一起而不愿分开。假设支付矩阵如图1。

这一博弈有两个纯策略纳什均衡，分别是两人都选择听音乐会和两人都选择看电影。在这种情形下，如果有一人先进行公开决策，则另一个人选择跟随是占优策略。而如果两人同时决策，那么这里得到的纳什均衡并没有提供采取占优决策的依据。如果主体都考虑了策略的概率指派，则双方就采取了混合策略。17混合策略的严格定义及详细讨论可参考[10]。下面我们用概率认知模型来描述协同博弈的混合策略及主体的认知状态。

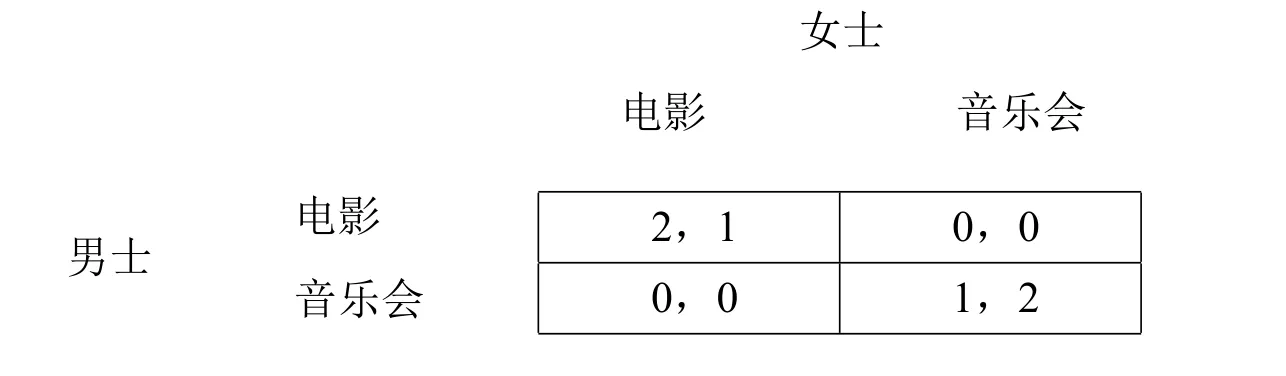
图1: 协同博弈支付矩阵

首先构造一个概率认知模型：给定主体集Ag={1,2}和命题逻辑原子公式集At={C1,C2,M1,M2}，依次表示主体1 选择听音乐会，主体2 选择听音乐会，主体1 选择看电影，主体2 选择看电影。这里我们用主体1 表示男士，用主体2 表示女士。令W={wn |n ∈N}，R1=R2=W2，令W4k+1={w4k+1∈W |k ∈N}，W4k+2={w4k+2∈W | k ∈N}，W4k+3={w4k+3∈W | k ∈N}，W4k+4={w4k+4∈W | k ∈N}。令A 是基于{W4k+1,W4k+2,W4k+3,W4k+4}据可允许赋值集运算封闭性要求构造而成的一个可允许赋值集，使得{W4k+1,W4k+2,W4k+3,W4k+4}⊆A。对于任意X ∈A，任意s,t ∈{1,2,3,4}，µi,w4k+s(X)=µi,w4k+t(X)。且对于任意X ∈A，存在w ∈W，使得对于任意q ∈[0,1]∩Q，都有µi,w(X)=q。V(C1)=W4k+1∪W4k+2，V(M1)=W4k+3∪W4k+4，V(C2)=W4k+1∪W4k+3，V(M2)=W4k+2∪W4k+4。M=〈W,Ri,A,µ,V〉i∈Ag，其认知关系如图2（省略了自反和传递关系箭头）。

图2: 概率认知模型M 中的认知关系

在没有达到混合策略纳什均衡之前，主体关于自己和对方的策略的概率是不确定的。这一点在模型中被描述为：对于任意主体i,j ∈Ag，任意c ∈[0,1]∩Q，都存在w ∈W使得M,w |=(Pj(Ci)=c)∧(Pj(Mi)=1-c)。关于主体的认知状态，易证。这表明，在这一博弈中，博弈双方都知道自己采取了混合策略，也知道对方采取了混合策略。

令主体1 选择听音乐会的概率为a，主体2 选择听音乐会的概率为b。在混合策略纳什均衡中，主体2 的混合策略满足等式1·(1-a)+0·a=0·(1-a)+2·a，主体1 的混合策略满足等式2·(1-b)+0·b=0·(1-b)+1·b。可表示为公式：

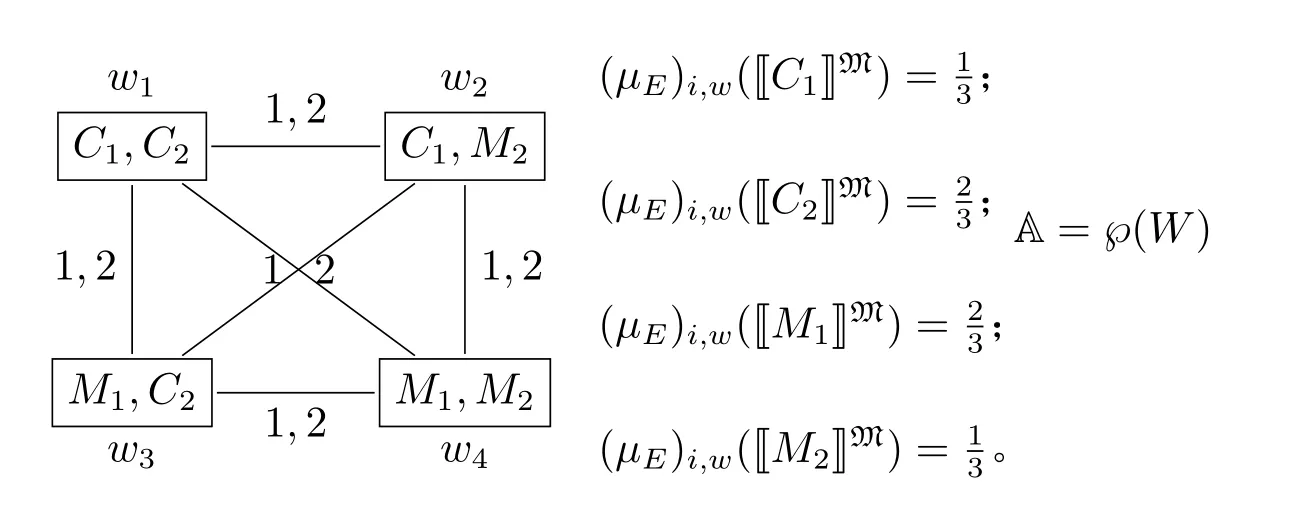
图3: 协同博弈纳什均衡的概率认知模型ME

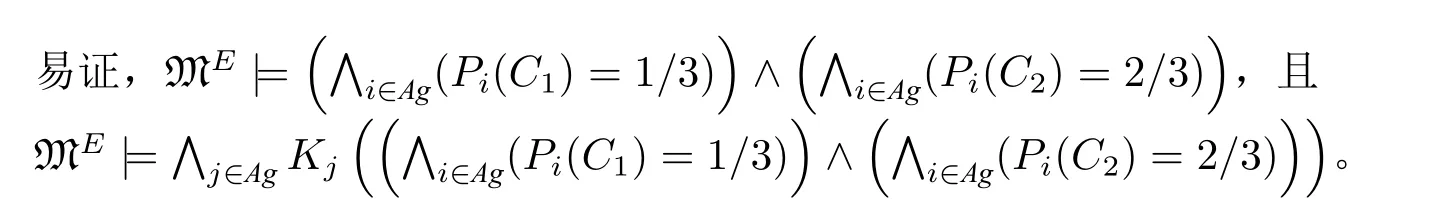
由此可知，在模型ME的任意可能世界上，任一策略的概率是确定的，也就是说，协同博弈有且仅有一个混合策略纳什均衡。同时，模型ME还表明，这个唯一的纳什均衡是两个主体的普遍知识。例1 还表明，概率认知模型可以借用认知算子和概率算子的叠加刻画主体对一个事件的概率不确定性。

5 结论与展望

本文在[4] 和[7] 的基础上提出了一个将概率函数建立在可允许赋值集上的概率认知模型，它为概率认知模型的可测问题提供了一种解决方案。这是继概率空间认知模型和离散概率认知模型后的第三种概率认知模型。本文比较了三种模型并指出，如果所有给定命题的概率都是可测的，与概率空间认知模型和离散概率认知模型相比，基于广义框架的概率认知模型在模型构造和语义定义上具有一定优势。

本文给出了一个基本的概率认知逻辑公理系统PELG，在未来的研究中可以考虑对PELG 进行扩张。文献[4]指出某些特殊的模态逻辑公式在一类特殊的广义框架上是有效的，文献[7]定义了一些特殊的概率函数并讨论了一些特殊的概率认知公理，这些在基于广义框架的概率认知逻辑中同样可以实现。本文在[7]和[8]的基础上，定义了一个典范概率认知模型，提出并证明了概率函数存在引理。存在引理是重要的，它保证了典范的概率函数是良定义的，但这一引理在已有文献中没有被提及，更没有得到严格的证明。本文采用典范模型的方法证明了PELG相对于概率认知广义框架类是可靠且完全的。

最后，本文运用基于广义框架的概率认知模型刻画了混合策略博弈的初始状态和混合策略博弈纳什均衡。通过分析可知，基于广义框架的概率认知模型可以描述混合策略博弈初始状态中主体的认知状态和概率的不确定性，也能够描述混合策略博弈纳什均衡状态下主体的普遍知识和概率的确定性。这为进一步运用概率认知逻辑研究混合策略博弈的认知变化和概率更新奠定了基础。

本文仅仅是基于广义框架的概率认知逻辑研究的一个初步尝试和开端，在这方面还有许多问题有待研究。在基础研究方面，未来的工作包括但不限于研究基于特殊广义框架的概率认知逻辑、基于邻域语义广义框架的概率认知逻辑、动态的基于广义框架的概率认知逻辑以及概率认知逻辑中公共知识的作用。在运用研究方面，可以运用这一逻辑讨论混合策略博弈如何从初始状态达成混合策略纳什均衡、讨论概率悖论和贝叶斯决策问题等等。