反推数学与无穷

康孝军

无穷一直以来都是数学哲学中的一个基本问题：数学中无穷集合或对象是否存在？一部分人认为：不存在。比如：严格有穷主义者就认为我们接触的时空与事物都是有穷的，因此仅仅存在有限的数学对象。自然，另一种可能的回答就是：数学中存在无穷对象。事实上，绝大部分数学工作者都或多或少涉及全体自然数集合等无穷对象。遗憾的是，不同数学流派的观点并未令彼此信服：一方面，严格有穷主义无法满意地解释无穷数学的可应用性；另一方面，如何认识各种无穷则是一个巨大的难题。

事实上，这种对无穷的探讨不仅具有哲学意义，也受到众多数学家的关注。希尔伯特甚至指出：“关于无限的本性的根本性的阐明，并非只属于专门科学兴趣的范围，而是人类理智的尊严本身所需要的”（[20]，第212 页）。而随着数学的不断发展，作为数理逻辑中热门的反推数学纲领给出了研究这一难题的新视角。本文在简述数学中的无穷概念后，将利用“反推”这一方法来探讨经典数学需要多大的无穷。

1 数学中的无穷概念

经典数学中包含无穷且大多数数学家日常工作中都会涉及自然数全集等无穷概念，因此，本节将暂时搁置无穷的知识论等问题，探讨数学实践中可能涉及的各种无穷概念。具体来说，首先，对潜无穷和实无穷进行了区分与简要述评。其次，梳理了数学实践中无穷概念，并指出康托继承了波尔查诺（B.Bolzano）的无穷概念思想。

1.1 潜无穷与实无穷

早在古希腊时代，哲学家和数学家就开始对无穷这一概念的探讨。阿那克西曼德（Anaximander）在探讨事物的本质时就涉及无穷这一概念。他认为事物的本质是“……无穷或者无限，一个永恒不朽的实体。万物由这一实体产生，又归于它”（[22]，第18 页）。阿那克西曼德没有对这种做出详细的解释，但哲学史家梯利（F.Thilly）指出：这里涉及的无限是一个具体的无限实体，而并非抽象的无限或无穷（[22]，第20 页）。无疑，这种形而上学的无穷显然不是数学中抽象的无穷概念。

亚里士多德对这种抽象的无穷概念进行了详细阐述。他在《物理学》一书的第三章中第4–8 节涉及无穷这一抽象概念。首先，亚里士多德在第六节中对“存在”进行了区分：“事物被说成‘存在’，一种是潜能的存在，另一种是现实的存在”（[28]，第85 页）。基于这一点，无穷也有两种可能的理解：潜在的或者现实的。不过，亚里士多德赞同的是潜无穷这一无穷概念。他进一步指出：“量在现实上不是无限的，但分起来却是无限的（驳斥‘不难再分的线’是不难的），因此，只有潜能的无限……不会有现实的无限……”（[28]，第85 页）。那么潜无穷究竟是什么呢？亚里士多德认为：“虽然一般来说，无限是这样的：可以永远一个接着一个地被取出，所取出的每一个都是有限的，但总是不同的……不是说它们是一个已产生的实体，而是说它们永远处在产生或灭亡的过程中”（[28]，第86 页）。

我们可以从算术的角度来理解潜无穷这一基础概念。无穷，顾名思义，就是有数不尽的对象。亚里士多德所表述的潜无穷概念，就类似于算术中的后继公理：对于每个自然数n，都存在一个直接后继n+1。这一后继过程会不断地重复下去，但永远无法完成，就是一种潜无穷的思想。潜无穷的观点比较能令人理解的，类似于计数，我们可不断地数下去，有这样一个潜在的无穷可能的过程。需要注意的是，亚里士多德这里的“无穷”更多的是指一种副词的用法1无穷这一概念在古希腊时期有三种不同的理解（[8]）：(1)名词；(2)形容词；(3)副词。名词是指形而上学或神学上的无穷这一实体概念。而亚里士多德否认实无穷的存在，故无穷不是某事物的属性，即不是形容词。亚里士多德使用的实际是“无穷地”这一副词形式：可以无穷地计数下去或无穷地分下去等。。事实上，亚里士多德之后，长达约两千年之间，数学家和哲学家中流行的都是潜无穷的观点。

实无穷则是指一个已经完成了的无穷。以自然数为例，实无穷就是指有一个包含所有自然数的集合。而对于实无穷而言，从亚里士多德开始，直到康托之前，在西方文化中绝大部分的哲学家和数学家都对其敬而远之。甚至可以说：大部分人还明确地反对实无穷。比如：高斯（J.C.F.Gauss）在1831 年就曾认为：“我抗议把无穷大作为一个完成的东西来使用，这在数学中是绝不允许的。无穷仅仅是一种说话方式而已。”（[7]）直到康托集合论的出现，实无穷才有了一个较为可靠的基础。之后，假定实无穷存在的公理化集合论系统ZFC 更是成为当今数学中一个广为接受的基础系统。

除了西方思想中的无穷观点之外，无穷这一思想在中国古代的著作中也有一定的体现，比如《庄子·天下篇》中的“一尺之捶，日取其半，万世不竭”。这种不断取其一半，永不停止的思想就是一种潜无穷的思想。国内部分学者，如杜国平还认为中国古代数学著作，如《九章算术·圆田术注》中也涉及实无穷的思想。（[21]）刘徽在该注中将求圆面积的方法表述如下：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”杜国平认为该方法中前面“割之又割”体现了潜无穷的思想，而“以至于不可割”则表示完成了，涉及到实无穷概念。不过，对于这一点，也有部分学者有不同的理解，例如鞠实儿和张一杰就认为这里仅涉及有穷可分的概念。这里表述的事实上是如下命题：“一个有穷物体经过有穷次分割，将终止于有穷大小的不可分割的部分”（[24]）。但不管是那一种观点，不同于西方对无穷概念的探讨，这些著作并未把无穷当成一个抽象的对象进行系统而详细的进一步研究。在这一点上，对无穷的研究类似于中国的逻辑学科，侧重于实际例子，而未进行系统理论探讨。这可能也与古中国数学重视实际的应用，轻视理论构建的传统有关。

1.2 波尔查诺的无穷概念

确切地说，康托并不是第一个对实无穷进行系统研究的数学家。事实上，在其之前，波尔查诺就在《无穷悖论》中开始对无穷的研究（[1]）。

波尔查诺在给出了“集合”2确切地说，波尔查诺首先给出的是“聚集”（aggregate）的概念，然后才给出集合（德语mengen，英译set）的概念（[1]，第76–77 页）。聚集与现代数学的术语中“类”的概念类似，就是把良定义（well defined）的事物或数字聚在一起。在波尔查诺看来，集合概念与聚集概念的差异在于，集合中个体的排列方式不会影响集合本身。简言之，集合是指去掉排列顺序差异的聚集。也有学者指出两者的不同之处在于是否“结构化”（[8]，第214 页）：集合具有这一特征，进而能识别。的概念之后，肯定了无穷集合的存在，如所有“绝对命题和真理”的集合。波尔查诺进而指出存在不同大小的实无穷集合。他考虑了两种不同的比较集合大小的方法（[1]，第96 页）：(1)配对的方法，也就是“一一对应”的方法；(2)真子集的方法。第一种是之后被康托采用采用的方法，第二种则是：若集合A是集合B的真子集，那么A是比B小的。波尔查诺通过一些数学实例发现，这两种不同的方法对于无穷集合而言，似乎存在着矛盾。考虑一个简单的例子，令A为闭区间[0,1]之间的所有实数的集合，B为[0,3]中所有实数的集合。利用方法(1)，每个A中的元素x都对应B中的3x，两集合大小是一致的。但利用方法(2)，A是B的真子集，A应该比B小。这两种方法导致的结果是矛盾的。基于此，波尔查诺认为这两种方法对于无穷集合而言，并不都适用。

遗憾的是，波尔查诺最终采用的是方法(2)，即真子集，来比较两无穷集合的大小。在波尔查诺看来，方法(1)仅仅适用于有限集合。对于无穷集合而言，“不仅进行计数的我们永远都不会到达A中的最后一项，而且由于无限集定义的作用，根本就没有这样的最后一项”（[1]，第99 页），所以“一一对应”会失效。鉴于此，无穷集合仅用真子集的方法来比较大小，这一矛盾也就根本不会出现。

无疑，波尔查诺对无穷的研究是跨时代的进步，第一次将无穷概念置于数学领域中进行探讨，无穷集合比较的两种不同方法也给康托的研究打下了坚实的基础。但是其无穷概念存在一些局限性，具体而言，有两点问题：一方面，他并未完全区分潜无穷和实无穷的概念。另一方方面，其无穷集合比较大小的方法局限在有限集合的思维。

首先，他并未完全从潜无穷概念中解放出来。仔细分析波尔查诺对方法(1)的反驳，不难发现他对实无穷的理解还不完全彻底，即并未完全区分实无穷和潜无穷。虽然他一方面承认了自然数全体的集合、[0,1]区间的实数集合等为实无穷的集合，但在比较集合大小的过程中，却依然将上述集合视为潜无穷的。在这种潜无穷的观点下，任意无穷集合A和B都是潜无穷，都永远无法到达最后的元素。在他看来，如果利用“一一对应”的方法，那么“B永远不会缺少与A的对象相配对这一事实”（[1]，第99 页），从而会导致A和B大小相等这一谬误。波尔查诺正是没有意识到自己对这两者的混淆，从而错误地根据这种相等性来否定了方法(1)，视上一段中的矛盾为这一方法从有限集合不当扩展到无限集合时导致的“幻觉”。

其次，无穷集合大小比较方法局限在有限集合的思维。波尔查诺虽然提出了两种不同比较的方法，遗憾的是，其并没有跳出有限集合的思维，采用了真子集这一想法继续来比较无穷集合。事实上，在波尔查诺之前，无穷的大小关系已有一定的认识，如莱布尼兹就认为“总有比至无穷远更大的全体”3英文为“there are always wholes greater than others ad infinitum”，转引自[7]。不过莱布尼兹并不赞同实无穷。他是基于此来反对无穷，认为无穷只是一个过程。。波尔查诺虽然意识到利用一一对应关系，两无穷集合的整体和部分之间可能相等。但基于有限集合的大小关系，错误地因为这种相等性而放弃了一一对应关系来比较无穷集合的大小。在他看来，一一对应虽然可以比较两个集合，但无法保证其相等性。

当然，应当指出的是：真子集的比较方法可能符合人们的直觉。如在对上世纪九十年代的澳洲大学数学系四十多名学生的调查中，采用真子集方法的比例为43%，差不多是一一对应方法的比例（23%）的两倍（[8]，第223 页）。作为第一个系统探索无穷的数学家，波尔查诺选择了这种直觉的方法，这无疑是可以理解的。但正是这一方法的遗漏导致波尔查诺错失了建立类似康托的无穷乐园的机会。

1.3 康托的无穷概念

康托之前，实无穷这一概念受到众多反对的一个原因是：实无穷集合与普通的有限集合的诸多方面都不太一样，如果完全套用有限集合的性质，会产生矛盾。比如，亚里士多德就使用了该理由拒绝实无穷：正常两个有限集合相加之和肯定是大于其中任意一个有限集合的。但对于实无穷而言，其与有限集合之和还是实无穷，不具有这种大小关系。（[28]）

希尔伯特曾以“希尔伯特旅馆”这一形象而生动的例子来揭示这两者的差异性：这个理想中的旅馆有无穷多个房间且都住满了人，一位新的旅客是否还能住进去？显然，不同于有穷旅馆，只需要每个房间的客人搬到相邻的房间即可。更进一步，再来奇数多位新的旅客呢？依然可以：只需n号房间搬到2n号即可。类似地，偶数多位也可以，自然数多位也就可以了。两倍的自然数和自然数好像是一样多的？传统的加法并不适应用自然数这一无穷集，这就要求对无穷集合的大小进行思考。

康托通过一一对应的方法详细探讨了集合的大小这一概念，并用集合的基数这一概念来表示其大小。一一对应的思想其实特别容易理解：当我们在生活中比较两种事物多少的时候，除了利用两者的具体数目外，还有另一种简单的方法：一个个比较。例如，比较装满苹果和橙子的两筐水果数量时，每人依次从两个筐中拿出水果，直到某一方无法拿出，此时无法拿出的一方就是相对来说数量少的。康托由此抽象出来“一一对应”的核心概念：“如果按照某种法则，它们彼此之间能够建立一种关系，使得一个集合中每个元素有且仅有另一个集合的元素与之对应”（[23]，第64 页）。

利用一一对应关系，康托给出了基数相等和小于等于这两个概念。如果两个集合是一一对应的，那么其基数就是相等的。也就是说，若两集合间存在一个双射函数，则其基数相同。如双射函数f(x)=2x就保证了全体偶数和全体自然数的基数相等。这意味着，对于无穷集合而言，部分并不是一定小于整体的，两者基数可能相等。如果一个集合A的基数与集合B的子集的基数相等，则称A的基数小于等于B的基数。进而可以进一步定义小于关系：小于等于关系且并非相等关系。利用基数的相等和小于关系，就可以比较两个无穷集合之间的大小了。4这种大小比较还需要一些预设，比如在ZFC 中，只有在预设选择公理的前提下，任意两集合的基数才是可比较的。

利用基数的概念，康托对实无穷的层次进行了初步划分，称有限集合和基数等于自然数集合的集合为可数集。显然，奇数、偶数集合都是可数无穷集合。事实上，康托进一步证明了有理数、甚至可数多个可数集的并也还是可数集。此外，康托利用对角线方法证明了实数集合并不是可数无穷集。全体实数集合和[0,1)之间的实数存在一一对应关系，故这两个集合的基数相等。那是否还有比实数更大的无穷集合呢？康托利用反证法证明了：任意集合的基数都是小于其幂集的基数的。据此，有以下这些不同大小的无穷集合：(1)全体自然数的集合和全体实数的集合；(2)对于一个无穷集合A，A和A的幂集（其基数比A更大）。

当然，随着集合论的不断发展，不可数基数有了更丰富的层次结构：如不可达基数、可测基数、武丁（Woodin）基数和强紧（strong compact）基数等。由于非集合论工作者很少接触上述基数，这里不再详述，有兴趣的读者可参考[5]。

2 反推数学与无穷

反推数学是弗雷德曼（H.M.Friedman）和辛普森（S.G.Simpson）所倡导的一种数学基础新纲领。该纲领是从经典数学所需的定理“反推”公理。简言之，就是在基底系统下，证明定理与公理（集）的等价性。一般而言，反推数学是在二阶算术的子系统中进行的，特别是“五大”子系统（RCA0，WKL0，ACA0，ATR0和5反推数学及“五大”子系统等详细介绍可参考[16]，初步了解可参考[25]。。大部分经典数学中的数学定理都在RCA0中可证或者在以RCA0为基底系统下，等价于其他“五大”子系统之一。作为一种希尔伯特纲领的部分实现，反推数学无疑继承了其对无穷的探讨。在对希尔伯特的有穷数学形式化中，已简要提及可利用反推数学来研究有穷和无穷概念（[26]）。在本节中，首先探讨哪些数学部分可以归约到有穷数学，然后利用高阶反推数学来分析经典数学中的无穷概念。

2.1 有穷归约

归约论也是一种对于希尔伯特纲领的部分实现（[19]，第438 页）。费弗曼（S.Feferman）的归约论指出：“数学M的一部分在由基础或概念框架F1所辩护的形式系统T1中表示。T1可从证明论上归约到由另一个更基本的框架F2所辩护的系统T2”（[3]，第364 页）。一般而言，基础或概念框架F1是一个包含是实无穷的以及非构造性的推理，例如ZFC。而更基本的框架F2则是包含有限组合对象的潜无穷概念以及可构造性的推理。这种归约的实现是通过编码和计算函数完成的。具体而言，“T1系统关于公式Φ 保守归约到系统T2”可分为以下三个步骤：

(1) 对T1和T2中的公式和证明序列进行编码。

(2) 存在一个部分可计算函数f，使得对Φ 中任一公式ϕ，如果m是公式ϕ在T1证明的编码，则f(m)就是ϕ在T2证明的编码。

(3) 步骤(1)和(2)都是在T2中可证的。当Φ 为所有等式公式“t1=t2”（t1和t2为系统中任意两个不含变元的项）的集合时，则称系统T1是可归约到系统T2。这种证明论意义上的归约6除了从证明论实现归约外，还可以从模型论的角度来探讨归约问题。费弗曼指出相较于模型论归约方法，证明论的方法提供更多有意义的信息等五个特征，是更优的归约方法。详见[3]。无疑是希尔伯特纲领的延续。这种归约论的思想与另一个概念“保守扩充”相关。称T1是T2关于公式Φ 的保守扩充，如果对Φ 中任一公式ϕ，ϕ在T1中可证，那么ϕ在T2中可证。显然，当T1关于公式Φ 保守归约到T2时，T1是T2关于公式Φ 的保守扩充。反之，则不一定成立。

费弗曼指出了几种常见的归约论的工作概念框架，例如：将无穷概念归约到有穷概念；将不可数无穷归约到可数无穷；将非直谓的定义归约到直谓定义以及将非构造性概念归约到构造性概念等。这里提及的第一种归约事实上就是辛普森所指出的反推数学对希尔伯特纲领的一种部分实现的方式，即“哪些可在二阶算术的子系统中的形成的无穷数学关于公式保守归约到初始递归算术（PRA）？”（[15]，第353 页）。PRA 一般被视为希尔伯特的有穷数学的形式化7辛普森赞同这一观点，更多有穷数学的探讨可参考[26]。，这种“系统S关于公式保守归约到PRA”的归约方式也被辛普森称之为有穷归约（finitistic reductionism）8辛普森在2015 年的讲座（[17]）中将有穷归约中的“ 公式”扩展为“ 公式”。由于现有数学实践中可有穷归约的系统均为公式，这一区别暂可忽略。，S也称是可有穷归约的。

自弗雷德曼和西格（W.Sieg）证明WKL0是可有穷归约的之后，寻找更大的可有穷归约的系统就成了进一步的任务。例如，布朗（D.K.Brown）和辛普森在WKL0中添加了一个康托空间2N的贝尔纲定理（Baire category theorem）的强形式，并证明了关于Π02公式归约到PRA（[2]）。由于很多组合原则与WKL0是不可比较的，在WKL0中添加组合原则成了对有穷归约的一种研究方法。

横山庆田（K.Yokoyama）在2013 年证明了WKL0∗加上拉姆齐定理是RCA0∗关于公式的保守扩充（[18]）。由此可知：WKL0∗加上其实是比较弱的。之后，帕蒂（L.Patey）和横山庆田在2018 年证明了WKL0加上规则是RCA0关于公式的保守扩充9参见[11]中的定理7.4。事实上，他们证明的是WKL0 +Γ 是系统关于公式的保守扩充，其中Γ 为{,ADS,EM}三个组合原则之一。，也就是说，在辛普森看来，WKL0+是可有穷归约的。而随着反推数学的不断研究，可有穷归约的无穷部分可能会进一步扩大。

2.2 超越二阶算术

按弗雷德曼和辛普森的设想，反推数学纲领是在二阶算术的子系统中进行研究的。而随着不断的改进，反推数学的主要议题也被辛普森限制在数学中的非集合论部分，即经典数学。在辛普森看来，经典数学可以粗略地等同于“可数数学”（[16]，第1 页）。但伴随着这一纲领的不断发展，二阶算术的限制带来的问题也慢慢开始浮现。

一方面，一些重要的经典数学中的定理无法在二阶算术中表示。在反推数学创立之初，弗雷德曼就1975 年就意识到反推数学并未覆盖经典数学中一些重要的研究领域，比如实数上的函数、巴纳赫空间（Banach Space）等（[4]）。另一例子是量规（Gauge）积分。该积分是勒贝格积分和黎曼积分的一种推广。量规积分提供了唯一接近费曼路径积分的形式化框架，与物理学的基础高度相关（[9]）。虽然量规积分在数学中非常重要，但其需要不连续函数和表亲引理（Cousin lemma），其中表亲引理涉及不可数的覆盖。而不可数的覆盖是无法在二阶的语言中表述的，这也意味着量规积分是超越二阶算术的，可能需要更高阶的语言。

另一方面，希尔伯特和伯奈斯在《数学基础》中的经典数学事实上是超越二阶算术的。二阶算术一般都认为可以追溯至《数学基础》中。但受到哥德尔不完全性定理的影响，大部分学者开始认为该论著的后期的形式系统已有一定的变化。希尔伯特和伯奈斯在后期的逻辑系统H 中已经开始涉及三阶参数与运算符（[14]），而二阶算术正是根据H 系统而来。事实上，桑德斯（S.Sanders）还进一步指出H的三阶运算符（epsilon）其实在希尔伯特指导的学生阿克曼（W.Acekerman）1924年的论文中对希尔伯特证明理论的概述中就出现了（[9]）。

辛普森在专著（[16]）中将二阶算术的源头归功于《数学基础》中的系统，而这一源头系统是超越二阶算术的。而随着反推数学研究领域的不断扩大，对不可数的部分数学也开始尝试使用“反推”方法来进行研究。在此基础上，自然的想法是去在找到更大的形式系统及其中的基底系统，来寻找反推不可数部分数学的可能性。

2.3 高阶反推数学

反推数学纲领的初衷是希望探讨“可数数学”，但“反推”这一基本方法无疑可以推广到不可数的数学部分。高阶反推数学就是尝试对经典数学中的不可数部分的一种尝试。该纲领由科伦巴赫（U.Kohlenbach）在2001 年提出（[6]）。简言之，科伦巴赫将二阶算术的语言扩展到所有的有穷类型，并将基底RCA0扩展为包括用于任意有穷类型功能的原始递归的版本RCA0ω，而该系统是RCA0的一个保守扩充。

高阶反推数学是把二阶语言扩充到更高阶的丰富语言Lω。二阶语言中，仅有自然数和自然数集，而Lω中还包含三阶、四阶……等对象，即自然数集合的集合、自然数集合的集合的集合……等。有穷类型的思想类似于哥德尔的T 系统。非形式而言，有穷类型包含0 以及任意两有穷类型对象之间的映射。特别地，可递归定义有穷类型符号1 为0 →0，n+1 为n →0。有穷类型有层次之分，0 为0层，ρ →τ 的层次为ρ 的层次加1 和τ 的层次中较大者。然后引入任意有穷类型ρ 的变量xρ，yρ……以及表达“两个层次为ρ 的类型对象相等”的二元谓词=ρ。其中，=0为自然数意义下的相等。而以ρ=(ρ1→0)为例，xρ和yρ相等就是指两者把任意ρ1类型的τ 映射后到0 层后的值相等，即xρ(τ)=0yρ(τ)。

基底RCA0ω包含以下六方面的公理10RCA0ω 的形式定义可参见[6]的第二节或者[10]的第2.1.2 节。：(1)关于常数0，0 层类型对象之间的小于关系、加法函数、乘法函数和等于函数的基本公理；(2)允许定义λ 抽象的K和S 组合子（combinators）的基础公理11K 和S 组合子是组合逻辑中的基本组合子，其中K(s,t)=s，S(r,s,t)=r(t)s(t)。直观而言，K 可视为类型常量组合子，对两个类型变量只返回第一个变量。S 可视为广义的合成组合子，先将第三个变量代入前两个变量后，再进行合成。；(3)递归常项R0的公理，该公理保证了对任意0 层m 和1 层f，R0可在0 层有穷类型对象上不断迭代；(4)外延公理，即如果任意两个ρ 类型的xρ和yρ相等（xρ=ρyρ），则两者在任意ρ →τ 类型的ϕρ→τ映射后的两个τ 类型的值也相等（ϕ(xρ)=τϕ(xρ)）；(5)Lω中无量化公式的归纳公理；(6)无量化公式的选择公理QF AC1,0。科伦巴赫证明了RCA0ω是二阶算术子系统RCA0的保守扩充。

除了RCA0外，其他“五大”子系统在高阶反推数学中都有对应的保守扩充12本段和下一段中涉及系统的形式定义可参见[9]中的第1.3 和2.4 节。。WKL0ω由费弗曼在归约论中提及，是指基底RCA0ω中加上WKL，即每个无穷二叉树都有一条路径。ACA0ω和则涉及两个不可构造的运算符的存在公理：µ2和S2。其中，µ2函数为费弗曼的µ函数。ACA0ω就是基底RCA0ω中加上µ2公理，该系统是ACA0关于公式的一个保守扩充。ATR0ω就是基底RCA0ω中加上ATR 公理，该系统是ATR0关于公式的一个保守扩充。而S2函数为苏斯林（Suslin）函数，直观而言，该公理可以决定一个公式是否成立。就是基底RCA0ω中加上S2公理，该系统是关于公式的一个保守扩充。

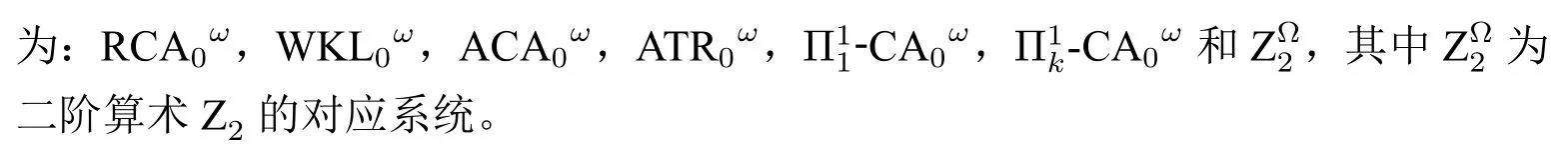
反推数学中，以RCA0为基底，可以找到众多与其他“五大”子系统等价的定理。高阶反推数学的情况类似，即以RCA0ω为基底，也能寻找其他四个对应系统的等价定理。例如：与ACA0ω等价的定理有（[12]）：

(1) 统一的波尔查诺–魏尔斯特拉斯定理，即存在函数F使得对任意X，若X是实数的有界序列，则该序列收敛到F(X)。

(2) 统一的一元拉姆齐定理，即存在函数Φ 使得对任意F，若F是N的一个有穷划分，则Φ(F)是F的一个无穷齐次集。

(3) 统一的k元拉姆齐定理，k为任意自然数；

(4) 存在函数Φ 使得对任意R，若R是一个可数的交换环，则Φ(R)是R的一个极大理想。

(1*) 存在函数Φ 使得对任意F，若F是树，则Φ(F)是F的完全核心（Kernel）。

(2*) 存在函数Φ 使得对任意F，若F是有不可数多条路径的树，则Φ(F)是F的非空的完全子树。

上述事实意味着高阶反推数学中，情况与二阶算术不太相同。例如，在二阶算术中，k元拉姆齐定理的强度是不太相同，而在ACA0ω的等价定理中(2)和(3)等价，统一的k元拉姆齐定理并没有区别。这并不是个例，与等价的定理(1*)是与等价的定理的统一版本，而(2*)却是与ATR0等价的定理的统一版本。由于反推数学考虑的是可数的数学对象，而高阶反推数学是不可数的，这两者的区别激发着一个自然问题的探讨，即经典数学究竟需要多大的无穷？

3 经典数学需要多大的无穷？

从归约论的角度来看，一方面，有穷归约指出部分的无穷数学S可以关于公式保守归约到PRA。公式涉及系统的一致性证明等有实质意义的语句。这意味者可有穷归约的系统S无法证明比PRA 更多的一致性断言。在辛普森看来：由于S中可证的有穷意义（finitistically meaningful）句子都在PRA 中可证，“S中的非有穷部分都可以在证明中‘剔除’，换言之，S仅仅是一个‘实用的虚构（convenient fictions）’”（[17]）。另一方面，高阶反推数学告诉我们：不可数无穷或更大的无穷可以归约的方式找到在更基本概念或框架，如可数无穷中的对应系统。这似乎意味着经典数学不需要多大的实无穷概念，通过归约的思想似乎可以逐渐对无穷进行“降维”：从不可数到可数，再从可数归约到有穷数学。

不过，从反推数学进一步研究发现：在处理某些高阶数学对象时，高阶反推数学是必需的，也就是说涉及到不可数无穷。对高阶反推数学的需求可以从两点来理解：二阶语言编码的局限性和不在常见系统中的定理。

第一点而言，在二阶算术中，通过编码可以对一些高阶的数学对象进行处理。例如：实数R 的子集、R 中的连续函数等。R 中的连续函数可以编码为二阶语言在完备的可分离度量空间中的五元谓词Φ(n,a,r,b,s)来进行定义（[16]，第85 页）。而且在假定WKL0成立的较弱系统中，二阶语言中的编码不改变与连续函数有关的定理的逻辑强度。但是对于其他一些高阶数学对象，如不连续的黎曼可积函数等，这一事实不再成立。黎曼积分中的阿泽拉（Arzela）收敛定理在二阶算术的编码中是在WKL0中可证的，但事实上，阿泽拉定理在高阶反推数学中，是在才可证，却在k为任意赋值的及这些系统的可数并构成的新系统中都是不可证的（[9]）。这表明：二阶语言的编码改变了这一定理的逻辑强度。这种强度的改变也提醒着：从二阶算术扩充到高阶算术，即从反推数学到高阶反推数学，并不是简单的一致推广，这种保守扩充是基于某些特定公式集的。直观而言，无法简单将不可数的情况归约到可数的情况，或者说，在这一归约的过程中一些性质可能会遗失。

第二点而言，在考虑如不连续的黎曼可积函数等不可编码的高阶对象时，高阶反推数学中也出现了一些不在“五大”子系统对应系统中的定理。阿泽拉收敛定理就是其中之一，而且事实上很难在一个较弱的系统中形式化。

不过，令人惊讶的是，桑德斯在近期发现：其中一部分定理可以通过ECF 翻译进行转化，从而与二阶算术中“五大”子系统对应（[13]）。直观而言，一个公式的ECF 翻译是指：该公式的类型为2 或更高的变量都由连续函数的可数表示代替。例如，对于海涅–博雷尔定理（HBU），即不可数的覆盖存在有限子覆盖。其对应的（HBU）ECF就是可数的覆盖都有有限子覆盖。桑德斯指出了利用ECF 翻译，将HBU、引导原则（bootstrap principle,BOOT）、Σ TR 和BOOT2转换的定理恰好对应二阶算术的“五大”子系统中的WKL0、ACA0、ATR0和其中，BOOT 定理来源于《数学基础》中的H 系统，是一种概括公理13BOOT 的形式化和更多介绍可参见[10]。BOOT 是指：任给一个二阶对象Y，存在自然数的子集X 使得n 是X 的元素当且仅当存在一阶函数f 使得Y(f,n)为零。虽然在ECF 翻译下，BOOT 对应于ACA0。但BOOT 是一种较强的原则，没有比∃3 公理更弱的概括公理能证明BOOT。，Σ TR 是ATR0加上BOOT 定理，BOOT2是指加上BOOT 定理。这种对应的转化被总结为：“当我们说A通过ECF 转换为B时，我们的意思是[A]ECF涉及一类连续对象，B立刻被认为适用于该对象……”（[14]）。此外，在这种ECF 翻译的转化下，其等价性的对应关系也保持不变。也就是说，两个等价的定理在转化后还是等价的。桑德斯将“由BOOT 及其同类组成的层次结构称为柏拉图层次结构（Plato hierarchy）”（[13]），而将上述转化的对应与等价事实称之为“柏拉图和哥德尔层次结构之间的联系”（[13]）。在桑德斯看来，这一联系为柏拉图的洞穴寓言提供了有力的例证。基于这一点，“柏拉图层次结构”这一称呼由此而得以命名。桑德斯基于其柏拉图主义而对这一证据给予了很高的评价，但显然的是，利用ECF 翻译的事实对柏拉图主义的论证是不太充分的。

但是利用ECF 解释，高阶算术部分可以规范地嵌入到二阶算术部分，这似乎意味着高阶算术的定理可以简化成二阶算术的形式。而从二阶算术推广到高阶算术时，高阶反推数学的例子意味着无法简单推广。不过，桑德斯近期在研究数学证明时还发现：“序列上的某些结果（可能是可数的）可以直接转换为关于网格（nets）的更为通用的结果”（[14]）。非形式而言，进过较少的修改，某些关于可数对象定理的证明可以得到其对应的不可数对象定理的证明。这意味着部分数学定理可以直观地推广到不可数的情况中去。

上述高阶反推数学的论证表明：对于特殊的高阶对象，不可数实无穷是必需的。但通过损耗的翻译，可将部分高阶算术简化为二阶算术。而且在某些特殊情况下，二阶算术和高阶算术中可直接转化。这意味经典数学对实无穷的需求事实上取决于实践数学中的“经典数学”包含哪些部分。当对经典数学的理解中不涉及R 中不连续函数等对象时，结合有穷归约中的“降维”，可能可数无穷，甚至希尔伯特意义上的有穷数学系统PRA 就足够了。而如果涉及R 中不连续函数等对象，显然不可数无穷则是必要的。利用归约论和高阶反推数学来加深对无穷的探讨将进一步为此问题提供更为准确的答案。

事实上，反推数学是从实用主义来寻找数学真理，结合“反推”方法的实用主义数学真理观将有助于这一问题的研究（[27]）。“经典数学”包含哪些无穷部分实际上基于我们对数学的认识与需求。换言之，无穷的需求取决于数学实践自身中数学的实用性。例如，那些不可达基数，如武丁基数等，对于非集合论学者而言都是十分陌生和难以理解的。自然，这些实无穷概念在证实其普及的实用性之前肯定不是必需的数学。但是，对大部分人而言，数学中的自然数、实数等都是所熟知的数学对象。基于此，实数这一实无穷可能是一个备选的回答。