高中数学复习课六环节教学模式及实施策略
河北省唐山市迁安市第四高级中学(迁安市第一中学西校区)黑丽丽
复习课是高中数学课的主要课型之一,是夯实双基,拓展知识,总结规律,培养解题能力的主战场。如何上好复习课,下面我从六环节教学模式解读利用向量解决三角形问题。在高考中,解三角形是重要题型,通常要和向量结合考查,今天我们就是要探索在我校推动的六环节教学模式下如何利用向量法探究三角形的中线、角平分线问题,抓住三角形“三线”及“四心”,能巧妙解决问题,并形成数学建模思想展开教学的。
一、导(情境导入)
复习课的导入要切入点准确,启发性强,“一针”即入本节课重点,迅速唤醒学生的思维,有情有境,情,就是利用老师的激情和对于问题深入理解和参悟去唤醒和激发学生的学习激情。境,就是教师要设计合理的境况,引发学生的思考,比如利用合理的考题或者是课本的习题设计情景,让学生感受到自己知识的不足,利用自己已经学过或掌握的知识不能很好的解决考题中的涉及本节课内容的问题,需要对知识进行再理解再认识才能解决问题,激发学生的学习兴趣和动力。然后才能高效的完成一节课的学习。
本节情景导入:在大屏幕上提出问题:三角形的“中线、角平分线”的向量表示是什么?
在三角形中,中线:
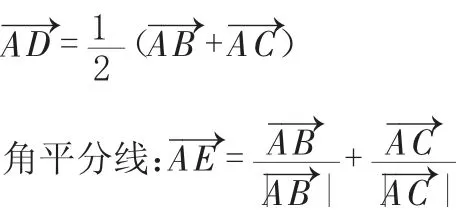
紧抓符号与图形,让学生深刻理解三角形的中线与角平分线的向量法表示。
二、标(目标展示)
即通过本节课学习一定要完成的任务和达到的要求。这个环节应该在情境导入的环节之后马上给出,使学生清楚地知道学习重点、难点,为下面几个环节确定好方向,增强教学的目的性,有的放矢。这个目标可以设计在课件和学生的预习案上,比如本节课复习的内容应当掌握的程度,学生应当掌握的技能与方法,寥寥几笔就可说明,不宜过长。
本节目标为:
1.通过向量法研究三角形的性质。
2.以三角形为研究对象,从向量角度对其性质再研究。
三、自(自学感知)
是在教师的指导下,学生带着问题,进行分析、理解、寻找重点、难点和发现其他问题的过程,是课堂教学“动静结合”中静的体现,是自主学习的环节,更是学生独立认知、思考的过程。这个环节依据复习内容的特点应该有这样几种处理方式:如果基础知识比较多,就可以设计一个预习案,将基础知识以填空的形式或问题的形式先发给学生,让学生课前预习,课前预习的预习案最好能收上来查看一遍,看学生的填写情况或回答情况,课上做到有针对性的讲解;如果基础知识比较少,就可以以填空或小问题的形式出现在学案,利用课上的时间进行自学,然后教师展示答案,学生进行对照,对不能明白的共性问题教师加以点拨。
本节自学感知:
问题探究:已知O是平面内一定点,A、B、C是平面上的不共线的三个点,动点P满足,且λ∈[0,+∞),则点P的轨迹一定通过△ABC的()。
A.内心B.外心C.重心D.垂心
变式:已知O是平面内一定点,A、B、C是平面上的不共线的三个点,动点P满足,且λ∈[0,+∞),则点P的轨迹一定通过△ABC的()。
A.内心B.外心C.重心D.垂心
此变式题恰巧就是对三角形角平分线的考查,角平分线的交点即为三角形的内心。
四、合(合作展评)
是学生之间释疑解惑的过程,是学习团队精神的体现,是学生在平等的基础上,互补、帮扶学习的有效途径。这个步骤除了生生合作,还要有师生合作,教师及时地对讨论的疑难问题进行启发、点拨,对各小组展示中存在的问题给予纠正,对发散思维的训练给予诱导、启发。这一环节是教学的中心环节,也是新课改理念的体现之处。在这里学生之间会有思想碰撞,教师和学生之间也会有思想碰撞。这里的展评,就可以小组展示并讲解,其他小组给予评价与补充。也可以是教师的讲解,最后师生达成共识,使知识得以升华。这样学生得到的知识才是自己的知识。这里最害怕的是走过场,不是真合作不是真探究。当然可以根据课的特点,有可探究的问题就探究合作,没有合适的问题就可以采用更合理的方式进行代替,不能千篇一律,最终的目标是为了让学生形成知识体系。
本节合作展评
例1在△ABC中,a,b,c分别是内角A、B、C所对的边,且满足
(1)求角B的值;
(2)学生会有不同做法,让学生展开思路,对比优劣。
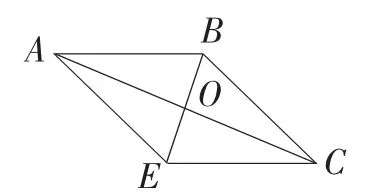
法一:补成平行四边形(中线)延长BO到E,使BO=OE,则四边形ABCE为平行四边形。
得a=1.
这是一种很不错的方法,紧抓向量加法的平行四边形法则。
法二:利用向量法表达三角形中线,即中线定理。
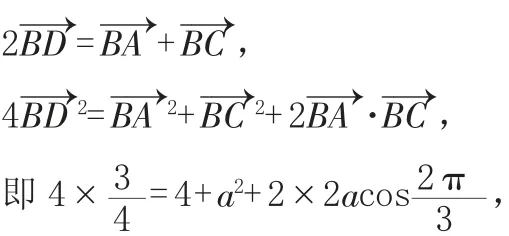
∴a2-2a+1=0,∴a=1.
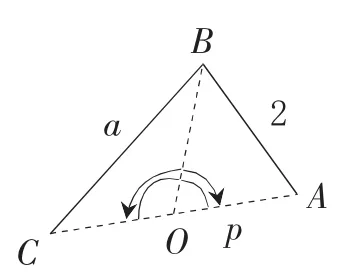
法三:由下图在△BOC中和△BOA中分别利用余弦定理解三角形,再由∠BOC+∠BOA=π,则cos∠BOC=-cos∠BOA,即可解出来,但计算量大,较麻烦。此方法学生想出来的较多,但大部分学生算不出来。教师要针对这种情况做出指导,指出这是一种重要方法,有时做题必须用这种思想。
练习1:△ABC内接于半径为R的圆,a,b,c分别是内角A、B、C所对的边,且2R(sin2B-sin2A)=(b-c)sinC,c=3.
(1)求∠A的值;
五、归(归纳拓展)
是对本节课的重点、难点问题的解决方法或易错、易混淆的地方归纳、总结、强调,而且通过强化训练对所学的知识、方法加以巩固。这个部分最好采用例题的方式进行完成,选定符合本节知识的例题进行知识点的总结和分析问题解决问题方法的升华。例题的选择一定要典型性和代表性,可以是模拟试题也可以是高考试题,最好是经过加工或改编的试题,功能性要强,一般是2~3个选择题或一个大题。主要是通过例题归纳分析问题的思路和解决问题的方法,目标是形成方法体系,把知识讲明白,让学生领悟透。
本节归纳拓展设置为:
例2已知在△ABC中,a,b,c分别是内角A、B、C所对的边,sinA=2sinC,2b=3c。
(1)求cosC;
分析:(1)由正弦定理和余弦定理易得出。(2)由角平分线性质:=2.
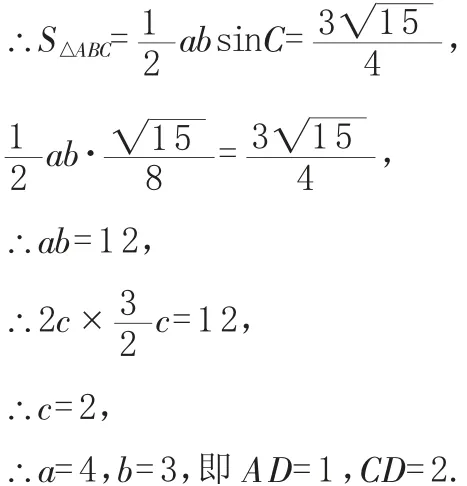

这类问题重点指导学生紧抓三角形角平分线的性质结合向量的模表达出来,使解题更加轻松。
六、测(达标检测)
是对本节课的学习内容进行测试,是检验课堂效率高低的重要一环,试题内容紧扣学习目标,要具有针对性、科学性,为评价的准确提供保证。这部分根据以上几个环节的时间来确定,如果以上都能在规定的时间完成的话,可以几个选择题或一个大题让学生体会学过的知识和方法,特别是例题所体现的方法的应用,让学生体会到学习方法前后解题的速度变化,体会到学习方法是有用的,学生才愿意学,才能达到教学的最佳境界。
本节达标检测设计为:
A.三边均不相等的三角形
B.直角三角形
C.等腰非等边三角形
D.等边三角形
2.在△ABC中,a,b,c分别是内角A、B、C所对的边,且满足2sinBcosA=sinA cosC+cosAsinC。
(1)求∠A的值;
(2)若b=2,c=1,D为BC的中点,求AD的长。
3.在△ABC中,D为BC上的点,AD平分∠BAC,△ABD面积是△ADC的2倍。
以上,以实例论述了六环节教学模式在数学复习课课堂上的具体应用及原理的剖析,教学环节为:导(情境导入)—标(目标展示)—自(自学感知)—合(合作展评)—归(归纳拓展)—测(达标检测),在实践中取得了良好的效果。总之,不同的教学策略会从不同角度来激发学生的学习欲望,使学生的学习潜能得到充分的挖掘,促进学生主动在课堂上分析问题、解决问题,实现学生学习能力的提高和个性的发展,进而实现有效学习和高效课堂。
——书写要点(三)

