独辟蹊径
——有心引力场天体运动的系统研究
周 游,俞潇潇
(华中师范大学 化学学院,湖北 武汉 430070)
由于天体运动都是曲线运动,其速度和加速度都是时刻改变的,所以难以求解速度和运行时间之间的解析解,而直接通过建立位移和速度的关系也是较为困难的,目前也未见报道[1-3]. 本文独辟蹊径地通过机械能守恒和角动量守恒分别巧妙地建立了有心力场运动的速度、时间和位置的关系,并对导出的椭圆轨道速度和时间公式用哈雷彗星进行实际检验.
众所周知,行星(绕行天体)绕恒星(中心天体)运动时,忽略它们和其它星体间的相互作用,绕行天体仅在中心天体万有引力作用下的运动轨迹只能是椭圆、抛物线、双曲线,且中心天体处在这3种曲线中的一个焦点上[4-6].
1 有心引力场的研究思路
由于引力属于保守力,所以绕行天体在运动过程中总机械能守恒,等于在该处的引力势能与动能之和.本文将利用守恒定律推导天体轨迹、轨道离心率和运行速度、运行时间之间的代数关系.
为了研究方便,我们以行星-太阳系统为具体的研究对象. 以行星近日点为直角坐标系原点,行星和太阳在近日点的距离为r,且太阳位于坐标系的x正半轴上;太阳质量为m1,行星质量为m2,行星轨道离心率为e.图1中的曲线为相同近日点和焦点的4种圆锥曲线轨道.
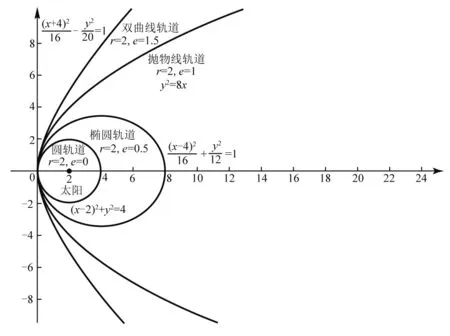
图1 以近日点为原点的圆锥曲线轨道
我们容易得到以近日点为坐标原点的圆锥曲线的方程和曲率半径(见表1). 同时,我们不妨设行星在近日点速度为v0,行星在运动时的投影横坐标为x.结合圆锥曲线顶点的曲率半径公式,对不同圆锥曲线轨道进行分类讨论.其关键在于速度的求解思路,因为椭圆、抛物线和双曲线轨道的速度是时刻改变的,直接方式难以求解.我们独辟蹊径地利用机械能守恒定律,其中引力势能只与距离有关,容易求解,而机械能和引力势能两者之差即得到动能,也就间接地获得了速度大小.

表1 近日点为直角坐标原点的圆锥曲线轨道方程和曲率半径
2 有心引力场的具体研究内容
2.1 机械能、速度和位置的关系
对于圆轨道而言,离心率e=0,行星绕行速率恒定,对于机械能E0和速度v00容易求解.
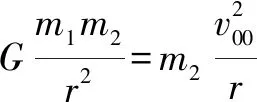
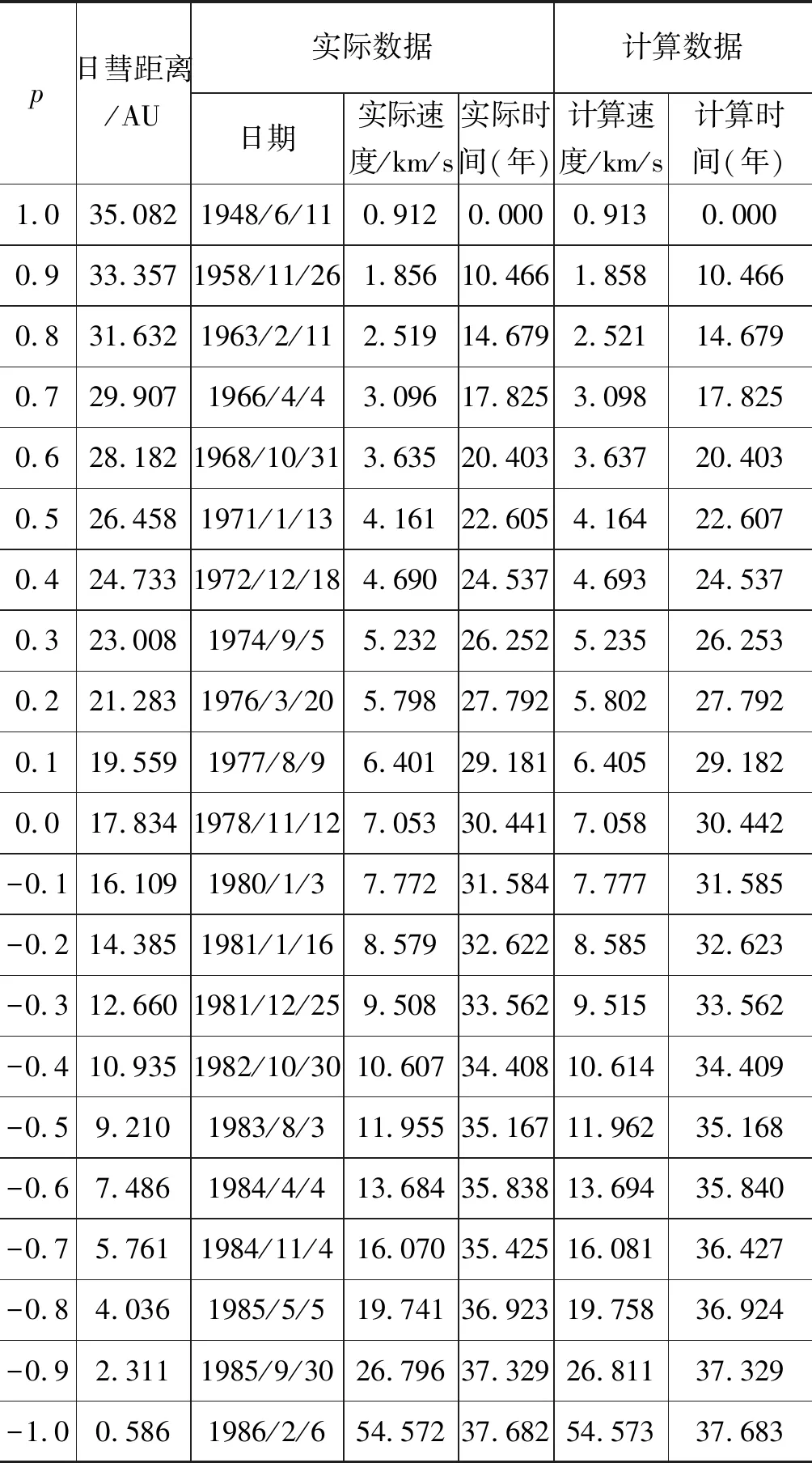
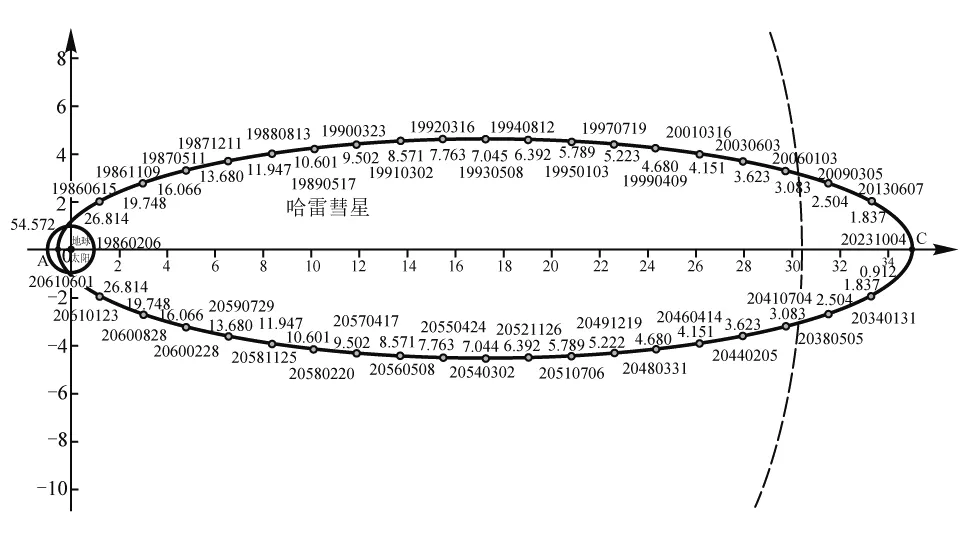
对于椭圆轨道,0 由 得 Ek1=E1-Ep1 即 得到 对于抛物线轨道,e=1,近日点的曲率半径ρ=2r,属于开放式轨道,速度时刻变化,但机械能也守恒.且轨道上任意位置行星和太阳距离为d=r+x.计算结果表明,当行星按照抛物线轨道运行很远时,最终行星速度趋于0. 由 得近日点速度大小 即 得 x→∞,最终速度v2f=0. 由 得近日点速度大小 即 得 x→∞,存在收尾速度,即 下面总结圆锥曲线轨道两天体距离、机械能、速度和位置的关系.在我们建立的坐标系下,可以发现它们的表达式高度统一,显示出有心力场运动的优美和谐! 顶点的曲率半径: ρ=r(1+e) 行星和太阳距离: d=r+ex 行星的近日点速度大小: 行星机械能: 行星角动量大小: 行星速度大小: 同理,也可以反过来断定.当中心天体质量和行星近日点位置确定时,行星近日点速度大小可以决定其轨迹. 因此对于特定的行星绕恒星系统,轨道上任意位置的速度大小唯一确定,且可得到其解析解.另外,由于行星、卫星、人造天体的运行轨迹都是椭圆,用椭圆轨道近日点速度v01、半长轴a和离心率e表示的速度公式更加具有实用性.将椭圆轨道中r=a(1-e)代入,最后得到的结果很对称. 速度和位置的关系已经完全解决,对于时间和位置能否建立关系呢?可以从开普勒第二、第三定律入手.首先引入面积速度h,开普勒第二定律描述了行星轨道的面积速度为定值,其本质就是角动量守恒.用椭圆轨道面积除以面积速度即可得到周期公式[9, 10].并且此部分的内容是将椭圆轨道的中心放在坐标原点,太阳在其x负半轴上,所涉及的坐标都设为x0. 根据角动量守恒定律,有 面积速度为 椭圆面积为 S=πab 则行星周期为 开普勒第三定律得证. 既然面积速度为常量,且以近日点为计时起点,扫过的面积除以面积速度即可得到绕行的天体运动到轨道上任意位置所需的时间,也就是将位置和时间联系起来了. 图2 椭圆轨道扫过的面积 关键在于求解在椭圆中扫过的面积,这部分面积等于椭圆部分面积和三角形面积之差(如图2所示).用定积分计算椭圆曲边形的面积,然后用面积除以面积速度即得运行时间. 以近日点为计时起点的时间即为 同理,容易得到以远日点为计时起点的时间: 上面得到了最终的运行时间和位置关系,其中-a≤x0≤a,发现几个特殊位置的时间完全符合实际情况(以近日点为计时起点). 运行时间和位置关系如下: 当x0=-a,则t=0. 哈雷彗星轨道是离心率很大的椭圆,这导致它在近日半程(-a≤x0≤0)和远日半程(0≤x0≤a)运动时间差异很大,用Stellarium0.18.3软件可以查询到哈雷彗星轨道参数如下:1986年2月6日到达近日点,1993年5月8日到达椭圆上顶点,2023年10月4日达到远日点.计算的两段时间比值和查询的实际数值十分吻合! 哈雷彗星轨道方程为 据前易得 计算得 实际是 如果将椭圆轨道的中心置于坐标原点,其速度公式会更加简洁对称,彻底解决了速度-位置、时间-位置的关系.而且可以进一步用真实的天体轨道验证其准确性. 任意位置速度大小公式为 任意位置时间公式: 近日点计时,有 远日点计时,有 最后,我们用哈雷彗星来验证公式的准确性和精确性,哈雷彗星的真实数据来源自天文软件Stellarium0.18.3. 我们选取了1948年远日点到1986年近日点的相关数据,并用我们的公式进行计算,发现速度和时间都和实际值吻合非常好(表2中展示了相关数据). 哈雷彗星轨道a=17.834 AU=2.667 95×1012m,e=0.967 1,实际周期T=75.367年 G=6.672 59×10-11N·m2/kg2, M=1.989×1030kg, r=0.586 AU=8.766 1×1010m 可求得 75.366年 表2 哈雷彗星的位置和速度、时间关系,实际值和计算值的对比 我们另外用Stellarium0.18.3的数据绘制了哈雷彗星1986年至2061年的轨道速度和时间图(如图3). 图3中哈雷彗星为顺时针方向从A点开始运行,横坐标位移梯度为0.1 a,对应每个点的速度单位为km/s,时间为年月日,灰色不完整的虚线轨道为海王星轨道. 图3 哈雷彗星轨道不同位置的时间、速度 本文独辟蹊径地利用机械能守恒简单地解决了有心力场下绕行天体的速度和位置的准确关系;通过面积速度解决了椭圆轨道运行时间和位置的准确关系. 并且还通过了哈雷彗星的轨道速度和运行时间进行实际验证,证明了公式的准确性和精确性. 本文系统解决的有心力场问题不仅存在于万有引力操控下的天体-中心天体运动,也存在于库仑力驱使下的电荷-中心电荷运动.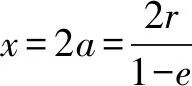
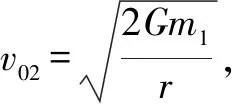
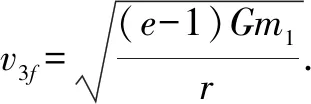
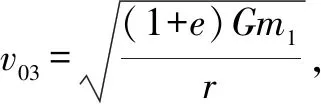
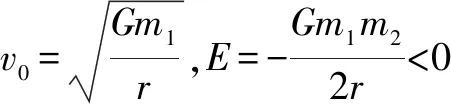
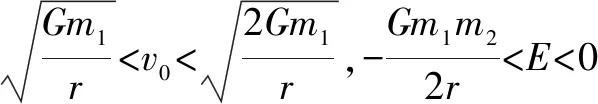
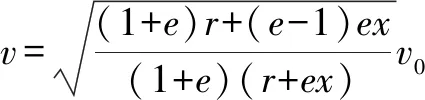
2.2 运行时间和位置的关系
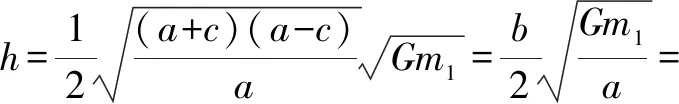
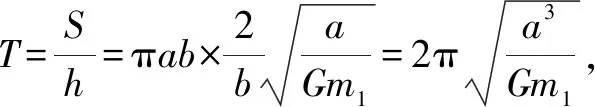
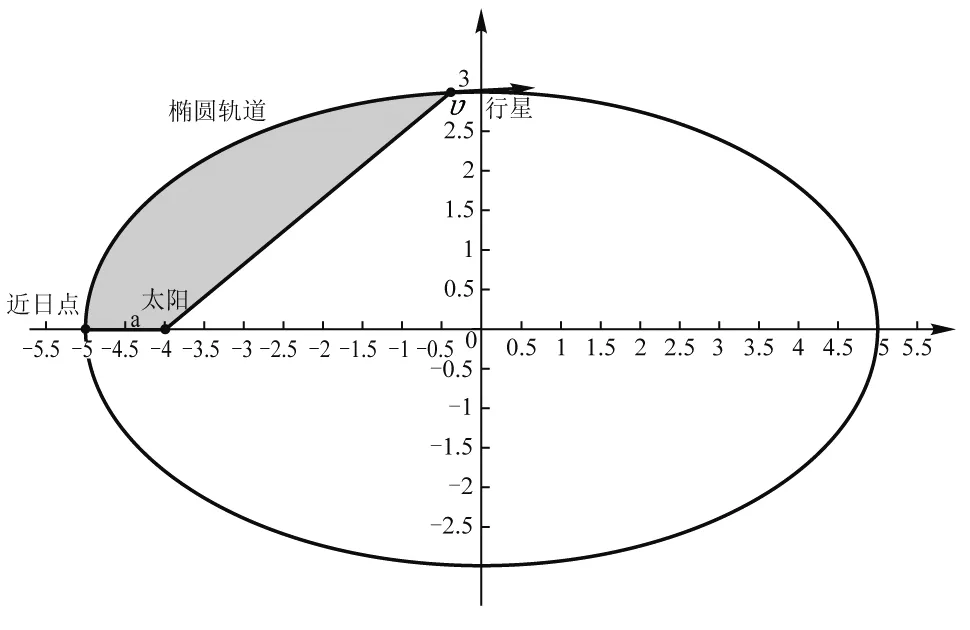
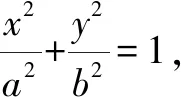
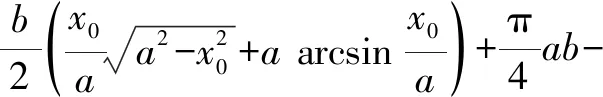
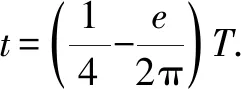
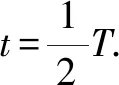

2.3 公式的总结和验证
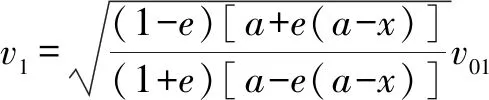

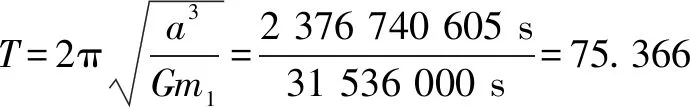
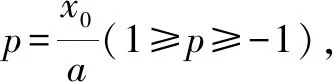

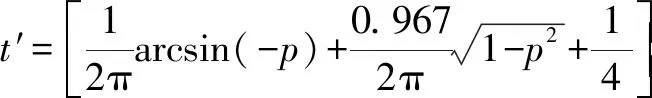
3 结论

