分层培养 显化隐性比较
——对一道初中物理比较题的探讨
周楠桦,吴 伟
南京师范大学教师教育学院,南京 210046
比较题是各地物理中考题中的常见题型。所谓的比较题是“比较某个物理量的大小或者判断某个物理量如何变化的一类问题”,其主要有两种类型。一类为横比较,即比较不同物体的同一物理量;另一类为纵比较,即比较同一物体在不同情况下的某物理量。而除了单纯的横比较、纵比较之外,还有二者的融合比较。本文选取了一道改编的中考物理模拟试题,它是一道横比较、纵比较、融合比较三者兼有的比较题,这类题近年来还在各地中考模拟中频繁出现,有一定的探讨价值。
1 例题及简析
1.1 例题
放在水平桌面上完全相同的两个烧杯中分别装有深度相同的甲、乙两种液体,把体积相同的两个实心小球A和B分别同时放入甲、乙两种液体中,小球静止时的情况如图1和图2所示,则下列说法中正确的是( )

图1 液体甲中的情况
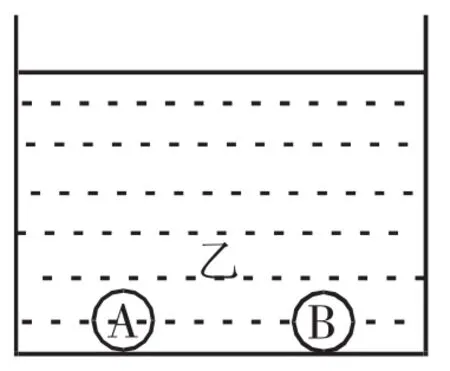
图2 液体乙中的情况
A.甲液体的密度大于乙液体的密度
B.乙液体中容器底对小球A的支持力大于对小球B的支持力
C.装甲液体的烧杯对桌面的压力变化量更大
D.装甲液体的烧杯底部受到的液体压强变化量更大
1.2 本题简析
选项A属于横比较,有两种解法:若运用物体的浮沉条件,则无需计算;若运用阿基米德原理与力的平衡,则需要简单计算,并运用比值比较法,关键式为
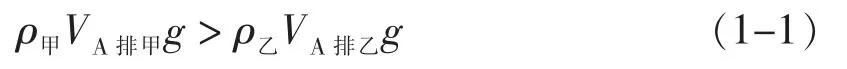
选项B属于横比较,解答时运用阿基米德原理与力的平衡,需要简单计算,并运用差值比较法得出结果,关键式为
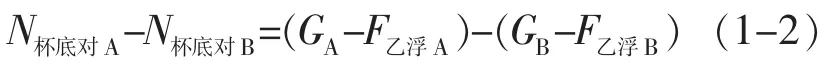
选项C属于融合比较,有两种解法:若运用内力与外力的知识,则无需计算;若运用力的平衡知识,则需要简单计算,并运用差值比较法。
选项D属于融合比较,有两种解法,都需要复杂计算。设烧杯底面积为S,小球体积为V,若运用液体压强公式,需用到中间值比较法,关键式为

若运用压强原始公式,需用到差值比较法,关键式为
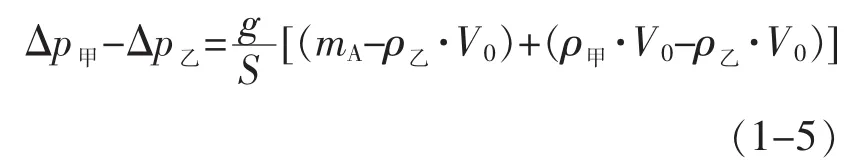
综上可得出表1,其中的“综合难度”是综合之前五方面的特征所得出的。
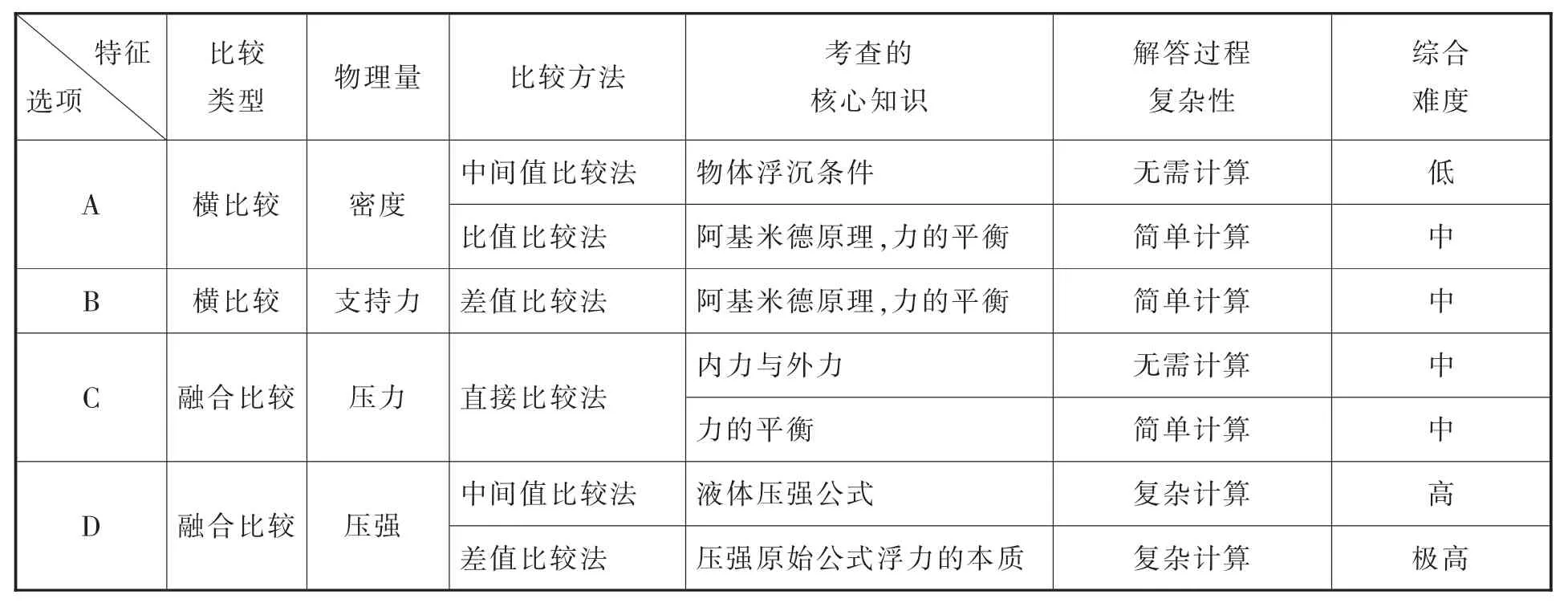
表1 各选项在六个方面的特征
显然,各选项解答过程复杂性与综合难度主要并不取决于比较类型与比较方法(如融合比较的选项C、运用比值比较法的选项A难度都不高),而更多取决于物理量的复杂性与所考查的知识难度(如运用压强原始公式的选项D解法二难度很高)。
2 对本题各选项、各解法的分层与教学建议
鉴于本题各选项、各解法在解答过程复杂性与综合难度两方面层次分明,因而在对本题进行教学时尤其要注意分层教学,可以将其分为五个层次,如表2所示。
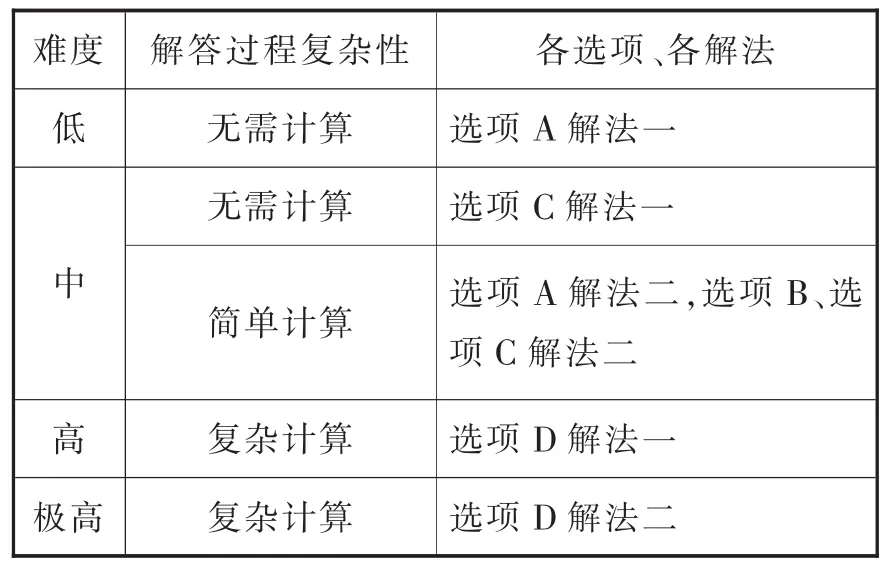
表2 按照综合难度与解答过程复杂性对比较题分层
如此分层后,中、低难度层次就囊括了无需计算、只需简单计算的A、B、C三个选项,要求占全班多数的中等水平学生在教学后能对其正确解答,也是集体教学的基本任务。
2.1 各层次的核心素养目标
根据《义务教育物理课程标准(2022年版)》中核心素养的“目标要求”,可对本题各层次的培养目标进行如下分析。
主要培养物理观念与科学思维:能将所学的浮力、密度等物理知识与实际情境联系起来,能从物理学视角观察、解释“小球A在液体甲中漂浮,在液体乙中沉底”的现象,能应用液体浮沉条件解决简单的实际问题;能对液体种类、小球浮沉情况进行分析并得出结论,具有初步的科学推理能力;能使用“盐水浮鸡蛋”之类简单、直接的证据表达自己的观点,具有初步的科学论证能力。
主要培养物理观念与科学思维:能将所学的二力平衡、牛顿第三定律以及延伸的内力和外力的关系等物理知识与实际情境联系起来,能从物理学视角解释两个烧杯所受支持力的异同。能对小球、液体、烧杯三者整体的受力情况进行分析并得出结论,具有初步的科学推理能力。
主要培养物理观念、科学思维、科学态度与责任:能将所学的阿基米德原理、二力平衡等物理知识与实际情境联系起来,能从物理学视角观察、解释液体甲、乙中的异同,解决简单的实际问题;能对小球、烧杯的受力情况进行分析并得出结论,具有初步的科学推理能力;乐于思考,具有探索自然的好奇心和求知欲,严谨认真,实事求是。
主要培养物理观念与科学思维:能将所学的阿基米德原理、液体压强公式等物理知识与实际情境联系起来,能从物理学视角观察、解释液体压强的变化;会用所学的“液柱”模型分析液体压强;能独立思考,用已知物理量表示液体甲、乙的密度,创新地用不等式、中间值比较法解决问题。
主要培养物理观念、科学思维、科学探究、科学态度与责任:能将所学的压强原始公式、浮力的本质等物理知识与实际情境联系起来,能从物理学视角解释液体压强的变化;能分析液体给小球的浮力、小球给液体的压力并得出结论,具有初步的科学推理能力;能独立思考,创新地用差值比较法解决问题;有科学探究的意识,能发现、提出问题,猜想“原始压强公式、液体压强公式与阿基米德原理之间的关系”,具有初步的观察能力和提出问题的能力;乐于思考,具有探索自然的好奇心和求知欲,有克服困难的信心和决心,严谨认真,实事求是。
2.2 各层次的分层教学建议
根据各层次不同的难度与所培养的物理学科核心素养的差异,提出分层教学建议。
2.2.1 “低难度-无需计算”层次的教学建议(选项A解法一)
该层次要求所有学生都能达到,教学重点在于调动学生有利于问题解决的直观经验。
“低难度-无需计算”层次有一个明显的特点,那就是无需科学规律,仅用一些适当的直观经验也可以解决问题。教师在教学时除了运用物体浮沉条件外,还可以退而求其次,先引导学生回顾教材中“盐水浮鸡蛋”的实验:在清水中原本沉底的鸡蛋,经过不断向水中加盐后,鸡蛋最终漂浮在水面上,这说明液体密度越大,物体浸入液体的体积越小(物体越容易“漂浮”)。学生有了这一直观经验,即可快速对选项A作出判断。
对于“低难度-无需计算”层次,教师对学困生的最低要求是运用直观经验解决问题,而在满足最低要求后,则应继续要求其掌握对应的科学规律。同时,教师应注意集体教学与个别教学的结合,如果学困生人数较少,可以课后进行个别教学,以节省课堂教学的时间。
2.2.2 “中难度-无需计算”层次的教学建议(选项C解法一)
该层次要求中等及以上水平的学生尽量达到。该层次并不多见,之所以在“无需计算”的情况下达到中难度,是因为运用了教材不作要求却与之紧密联系的“延伸知识”,教学重点也正是该“延伸知识”及其运用。
一般来说,不会出现只有运用延伸知识才能解决的题目。换言之,往往会有教材知识与之对应,它们分属于一个选项的两种解法。以本题选项C为例,它的解法一属于“中难度-无需计算”层次,解法二属于“中难度-简单计算”层次,解法一运用的延伸知识可以看作是解法二运用的教材知识的结论,因而在教学时可以先讲解法二,对多物体构成的系统做受力分析,在此基础上再讲解法一,即“内力与外力”。
2.2.3 “中难度-简单计算”层次的教学建议(选项A解法二,选项B、选项C解法二)
该层次要求中等及以上水平的学生都达到。该层次是比较题的主体层次,囊括了大部分选项与解法,教学重点是运用相关知识有条不紊、规范准确地解答问题。
以选项A解法二、选项B、选项C解法二为例,它们都应用了阿基米德原理、力的平衡,解题过程都是受力分析再比较力的大小,在中等及以上水平的学生能力范围内,因而教师应当向学生强调该层次的基础性,在教学时把它当作计算题,作出规范、准确的解题示范。
2.2.4 “高难度-复杂计算”层次的教学建议(选项D解法一)
该层次要求中等及以上水平的学生尽量达到,一般达到该层次时已足以正确解答本题。教学重点是以核心知识为解答之“锚”,“锚”前准备需要使用的各物理量,“锚”后对得出的表达式做数学处理。
以本题选项D解法一为例,它的“锚”就是液体压强公式,解答正是围绕其展开的。教学时,教师可以先引导学生明确所求的物理量是液体压强,据此写出液体压强公式(在公式所在的黑板位置上下方都留空),逆向思考“该公式需要用到什么物理量”,在公式上方求出密度、液体高度差的表达式,最后再在公式下方对两个压强差做数学处理。
2.2.5 “极高难度-复杂计算”层次的教学建议(选项D解法二)
该层次要求学有余力的学生尽量达到。该层次难度极高,很少出现,虽然考查的知识一般不超出书本,但却要求学生对各知识点融会贯通,甚至要进一步理解物理公式、物理规律的本质,而这也正是该层次的教学重点。
以本题选项D解法二为例,其解答要求理解浮力、压力、液体压强这三个物理量在逻辑上变化的先后顺序:首先,物体与液体开始接触,给液体一个向下的压力;接着,原本在物体下方的液体受到压力,被挤压到物体两边,形成液体高度差;根据液体压强公式,不同深度处的液体压强不同,与液体接触的物体表面各处受到不同的压强,而这些压强差最终在物体受力上就表现为浮力,这个浮力可以用阿基米德原理求得。
教师在进行教学时,要注重科学探究。首先引导学生回顾阿基米德原理、压强原始公式、浮力本质这些知识点,再提出对能否使用压强原始公式的问题,对各物理量之间的深层逻辑关系提出假设,接着画图呈现各阶段的现象(最好用自制动画),用物理规律解释物理现象,探究、总结各物理量之间的联系,最后逐步示范解答。
值得注意的是,“极高难度-复杂计算”层次对学生的物理观念、科学思维、科学探究能力要求都很高,一般只有极少数学生能够掌握,如果在集体教学中贸然展开,可能反而不利于大部分学生的理解,因而建议主要对学有余力的学生开展个别教学。
2.3 总结各层次的教学特点
由以上讨论,可总结各层次的教学特点,如表3所示。
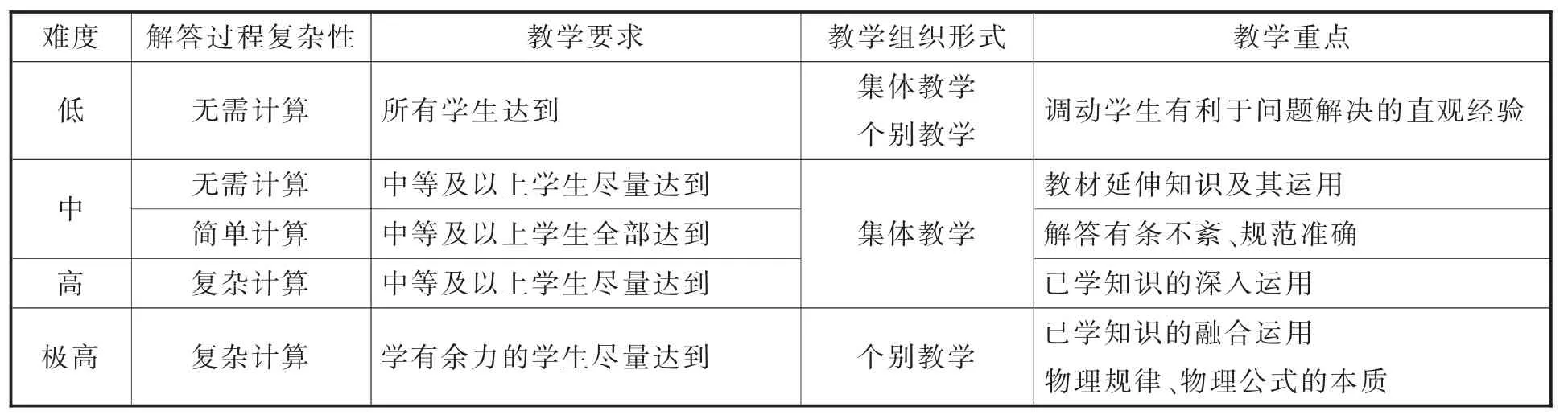
表3 本题各层次的教学特点
显然,除了“中难度-无需计算”与“极高难度-复杂计算”这两种不常见的层次之外,各选项综合难度与其解答过程复杂性高度相关:低难度-无需计算、中难度-简单计算、高难度-复杂计算。一般来说,这三个层次在选项中的个数为1:2:1,由此可以归纳比较题常见的“三层次”,如表4所示。

表4 比较题常见三层次的教学特点
3 显化“隐性比较”的教学建议
针对比较题,除了可以进行分层教学之外,还应注意如何根据题干中的“显性比较”进行分析,显化“隐性比较”。
题干中,有文本中的条件与图片中的现象这两类“显性比较”:文本中有6个“相同”条件——“烧杯同在水平桌面上”“烧杯完全相同”“液体深度相同”“小球体积相同”“小球都是实心的”“小球都是静止的”;1个“不同”条件——“甲、乙两种液体种类不同”;图片中有2个“不同”现象——“液体乙的高度比液体甲的更高”“液体甲中A漂浮,液体乙中A沉底”;图片中有1个“相同”现象——“液体甲、乙中小球B都沉底”。
3.1 补全隐性的“比较对象”
根据文本中的三个“显性比较”——“烧杯同在水平桌面上、烧杯完全相同、液体深度相同”,可以推理出一个“隐性比较”——“放入小球前,两烧杯的液体高度在同一水平线上”。这是一步非常简单的推理,但认识到这一点后画出示意图,就可以补全“放入小球前两烧杯的状态”这对比较对象,为之后的纵比较(选项C、D中融合比较的前半部分)做准备,从而大大提高比较的直观性,提高教学效果。
3.2 把握隐性的关键物理量的比较
在大量“相同”的前提条件下,两个烧杯中却呈现出种种“不同”现象,其根本原因就在于“液体密度不同”。液体密度是本题的关键物理量,液体密度的比较也是判断各对物理量大小的关键,但它是一个“隐性比较”,需要由题干中已知的“显性比较”——“液体种类不同”推理而来。“液体种类不同”是文本中唯一一个“不同”,但不同种类的液体可以在颜色、沸点等方面不同,并不单指“密度不同”。从笼统的“种类”推理到具体的物理量“密度”这一步是从实际问题向物理模型跨越的重要一步,需要学生有“对信息的有效性、客观性作出判断的意识”和“有初步的信息收集、分析概括能力”。
此外,“液体密度不同”这个“隐性比较”的显化还有另外两方面的依据。宏观方面,纵览本题可以发现其考查的核心是阿基米德原理,那么液体密度就是绕不开的关键;微观方面,本题选项A就是比较液体密度,其也是解答另外三个选项的必要条件。
4 总结
对于比较题教学,教师不仅可以着眼于各选项考查的物理知识,还可以将碎片化教学整合成多层次的体系,根据比较题各层次培养的核心素养目标及教学特点开展教学。除此之外,还应注意对“显性比较”的推理,对“隐性比较”的显化。

