多角度剖析问题 提升科学思维素养——一维弹性正碰的简化计算和启示

翟佑彬，栾 丽，李忠相

重庆市第一中学校，重庆 400030

在《普通高中物理课程标准（2017年版2020年修订）》中，提出了四个学科核心素养，其中“物理观念”是各素养的基础，代表知识的内化；“科学思维”与“科学探究”对应关键能力，“科学态度与责任”属于必备品格。其中，科学思维包括模型建构、科学推理、科学论证、质疑创新等要素，对应物理学科5大关键能力中的推理论证能力、模型建构能力、创新能力等。可见，提升学生的关键能力的核心在于科学思维素养的提升。多角度分析、多方法解决同一物理问题有利于训练学生思维的新颖性和灵活性，提升学生关键能力，下面以一维弹性正碰问题为例对此进行探讨。

一维弹性正碰是高中物理常规教学和物理竞赛活动中常见的物理过程，其求解过程通常较为复杂。为快速求解此问题，在实际教学中研究、总结出了六种不同的简化计算方法。

如图1所示，质量为m的弹性小球以初速度u运动，与另一质量为M、速度为u的小球在同一水平面上发生一维弹性正碰，求碰后两球的速度v和v。

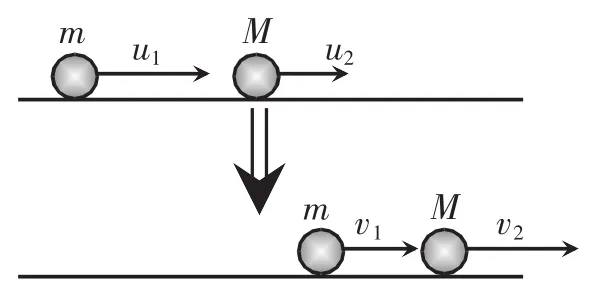
图1 碰撞过程示意图

1 直接消元法，特解指引简化求解思路

直接将一个方程的未知数表示出来，代入另一个方程消元。这种方法有时候容易因为形式过于复杂而使人迷失方向，如果有容易发现的特解指引，往往思路会更加明确。

碰撞前后，由于动量守恒和机械能守恒，分别有

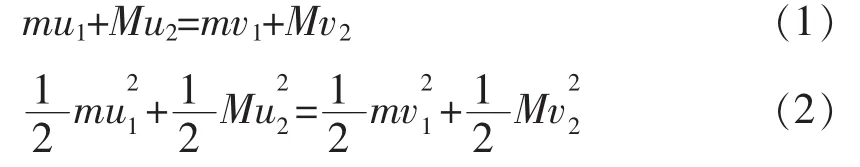
初学者第一次遇到这两个公式，第一反应是直接代入消元。但是尝试之后发现计算越来越复杂，便中途放弃，改用它法。事实上，直接消元未尝不可。 由（1）（2）式分别可得

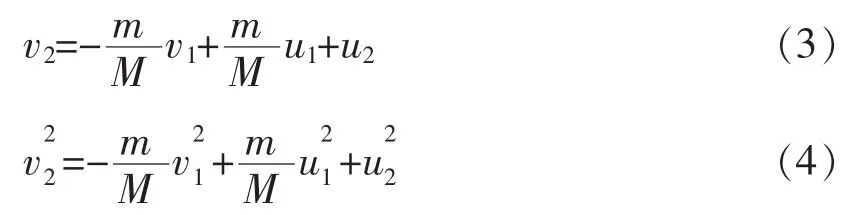
再将（3）式平方后与（4）式消掉 v，有

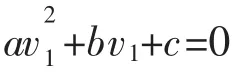
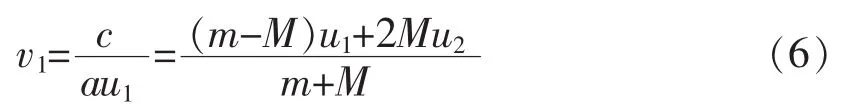
代入（3）式即可得到

此外，当我们注意到u应当是v的一个根，这就意味着（5）式一定包含（v-u）的因式，于是按此指引，也可将（5）式化简为

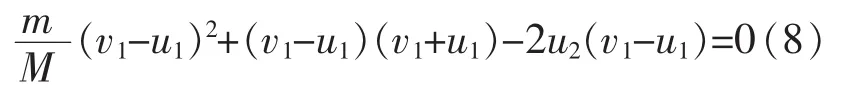
对于碰后状态，v≠u，可由此消掉（v-u）因式，实现对原表达式的降次，使之成为一次方程，后续求解这里略去。

可见，由物理规律发现特解，对化简复杂表达式有非常好的指引作用，这一思想在复杂运算中应用较多。

2 整体消元法，恢复系数替代能量方程

将多个方程中的一些表达式整体消元，可能让方程整体变得简洁。如果新的方程对应明确的物理含义，也可以越过整体消元这一步骤，直接按物理意义写出新方程。

对此问题，通常的简化求解方法是将（1）（2）式分别移项变形为

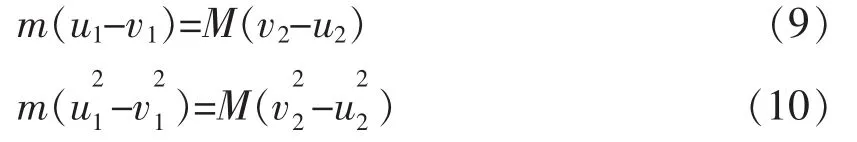
由于碰后 v≠u，v≠u，两式相除整体消元可得

再将（11）式和（1）式联立即可容易解出结果。事实上，（11）式正是弹性碰撞恢复系数为1的结果，即

所以，在弹性碰撞问题中，往往可以用恢复系数为1的表达式替代能量关系式，直接和动量关系构成一次方程组，问题求解大大简化。

3 质心参考系法，零动量要求速率反比于质量

质心系是一个非常特殊的参考系，有很多特别的性质，比如质心系是零动量系。合理利用这个特点，也可以简化运算。

在质心系下，系统的动量一定为零。由两个物体组成的系统，其速率必然和质量成反比。如图2所示，此问题中，碰后两小球一定有

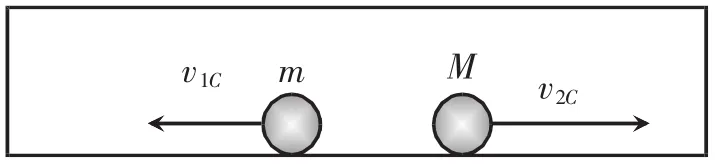
图2 碰后质心系

又因为弹性碰撞，碰后相互远离速率等于碰前相互靠近速率，有

由以上两式很容易写出

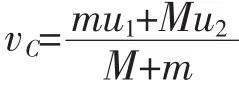
以上两式的结果均包含两项，各自的含义非常明确，通常可以做到直接写出结论，运算过程进一步简化。

4 转换参考系法，借用动碰静相关结论

如果以其中一个物体为参考系，就可以将问题转化为我们熟知的运动物体碰静止物体的模型，借用相关结论可以迅速找到结果。

如图3所示，如果选择被碰小球M碰前与之同速的惯性参考系，那么问题转化为m以（u-u）与静止的M发生弹性正碰，其结果是大家熟知的，即

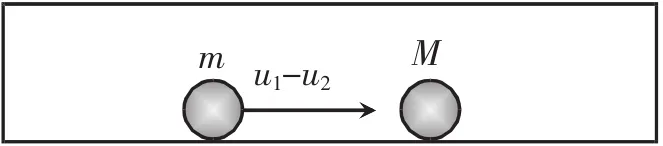
图3 碰前M参考系

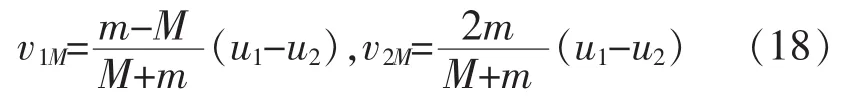
再加上该参考系的牵连速度u，可得

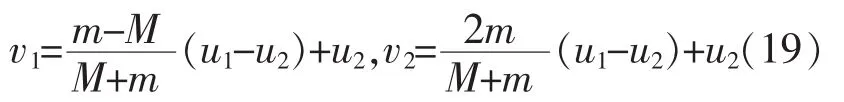
以上两式的结果也均包含两项，各自的含义同样非常明确，通常也可以做到直接写出结论，实际运算过程比质心参考系法更简洁。

要说明的是，这里选用的是与小球M碰前相对静止的那个惯性参考系，这个参考系在碰后依然具有牵连速度u，整个过程中参考系的牵连速度没有发生改变，故不必引入惯性力，动量和机械能守恒均得以保证。

5 叠加原理法，线性方程组的必然性质

如果一组方程都是线性方程，那么往往可以用叠加原理把多个因素分解成几个因素单独考虑，有效降低问题的复杂度。

此问题的结果可由（1）式和（11）式解出，这两个式子均为以速度为变量的线性方程。于是可以将此过程“分解”，将原碰撞过程视为m以速度u和静止的M弹性正碰（以下称为“碰撞I”），以及M以u和静止的m弹性正碰（以下称为“碰撞II”）的叠加，如图4所示。

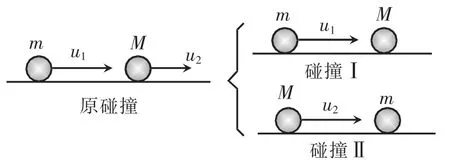
图4 碰撞叠加示意图

对于碰撞I，碰后两球速度分别为

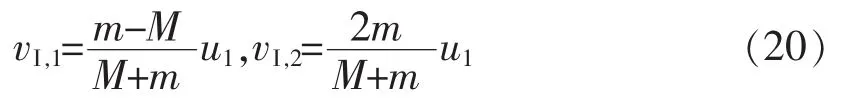
对于碰撞II，碰后两球速度分别为

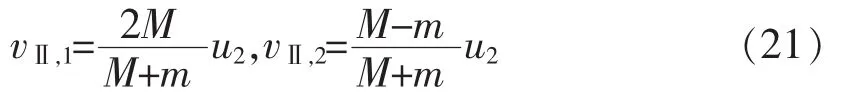
结果也相应叠加，即为原碰撞碰后两小球的速度

线性方程对应的叠加原理在线性电路求解过程中应用较多，但在力学中应用比较少。在这个问题中应用同样可以将计算过程简化到可以直接写出结论的程度。

6 共速中间态法，对称过程必有对称结论

从问题的对称性出发，往往能在复杂的关系中快速找到物理量之间的规律，从而为复杂问题快速找到简单解。

碰撞过程中，一定存在一个形变量最大的状态，此时二者共速，可称为共速态。由动量守恒定律

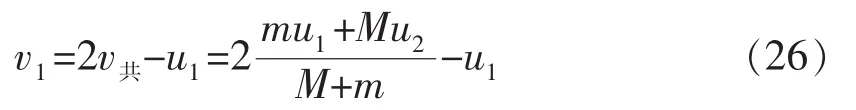
同理，M小球的初末速度平均值也正好是共速态的速度，即

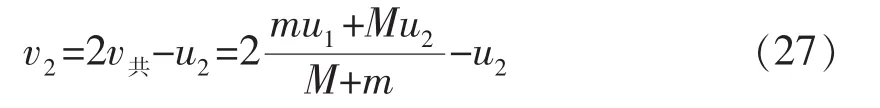
上述结果的形式也保留了两项，以使表达式的含义更清晰。使用这个方法的计算过程更加简洁。

上述六种方法是在教学过程中逐渐总结出的，本文给出的是一般情况的表达式计算和结果，如果有具体的数据，或质量倍数关系，或速度倍数关系，计算过程均会比本文的计算更简单，限于篇幅就不再一一举例验证。对于这六种方法，可以举出一些数据，用不同的方法验算，熟悉计算思路，对比计算的难易，挑选一两种自己最容易接受的方法熟练掌握。这几种方法的原理，有的比较好理解，有的比较抽象，在实际教学中要根据学生的情况进行筛选，切不可死记硬背，避免变成单纯地套用数学公式而忽略了对物理过程的分析和物理规律的理解。

物理思维的灵活性是指对某一具体思维过程来说，并没有固定的模式和步骤，能从多角度审视问题、全方位综合分析问题、采用多种方法解决问题。一维弹性正碰过程的求解，本就是动量与能量双守恒的二元二次方程组的求解。通过“特解指引简化求解”“恢复系数替代能量方程”“质心参考系法”“转换参考系借用动碰静法”“线性方程对应的叠加”“共速中间态对称法”六种简化办法，利用物理规律及结论指引数学方程组的求解，对拓宽学生视野、训练学生科学思维、提升学生关键能力具有积极的作用。