改进的增量式动静结合协同过滤方法

武 美，丁怡彤，赵建立+

1.山东科技大学 计算机科学与工程学院，山东 青岛 266590

2.东北林业大学 信息与计算机工程学院，哈尔滨 150040

随着科技的发展以及互联网的普及，用户可以在短时间内获得大量信息，但在这其中也包含了一大部分用户可能不感兴趣的信息，因此如何从海量的信息中快速对用户建模并为其推荐感兴趣的内容是本文要解决的主要问题。个性化推荐技术定位于目标用户的兴趣，从用户的历史浏览路径或操作信息中挖掘并识别出用户的兴趣所在，并主动向用户进行资源与信息的推荐。推荐技术的出现可以给用户节省出大量的时间与精力，而协同过滤是推荐系统所采用的最为重要的技术之一。其原理是根据相似用户的兴趣来推荐当前用户没有看过但是可能会感兴趣的信息，所基于的假设是：如果两个用户兴趣类似，那么很有可能当前用户会喜欢另一个用户所喜欢的内容。其中矩阵分解是处理协同过滤中较常用的方法，矩阵分解具有较高的准确性和扩展性，本文也采用矩阵分解的方法来进行评分的预测工作。在现实世界中，用户的行为累计往往在短时间内快速增长，推荐系统应能够适应这种变化，并在短时间内根据用户的实时数据更新推荐。因此，增量式设计在推荐系统中显得尤为重要。一旦推荐系统能够对这种数据爆炸做出快速的响应，相应的用户兴趣模型的构建就会更加灵活和具体，用户的忠诚度和满意度也会得到进一步的提高。本文的主要工作是在基于矩阵分解的基础上通过添加过滤机制对预测过程进行优化，以达到减小计算量、节省运算时间的目的，同时采取一种增量式静态的方法确保在减小时间消耗的同时保证一定的精度。

本文的主要贡献如下：

（1）将预测部分划分为增量部分和静态部分，保证精度的同时提高预测的效率。

（2）将训练数据按照一定标准划分为不同的区域，对不同区域采取不同的计算方法，有效提高计算效率。

（3）对数据的训练过程采取过滤机制，有效提高计算效率。

1 相关工作

在增量计算的之前相关研究中，Luo 等人提出了一种I-KNN（incremental K nearest neighborhood）模型，在Miranda 等人提出的RS-KNN（random subspace K nearest neighborhood）模型的基础上减少了存储复杂性，同时采用广义骰子系数保持了预测精度，但相应的计算复杂度增加。

Wang 等人提出了将聚类技术和非负矩阵分解结合的方法来进行评分的预测工作，通过一种快速聚类方法将聚类的个数作为矩阵的维度可以实时更新，避免设置的固定维度造成在数据量较小时造成的计算浪费，但是将聚类的簇数作为维度的定义缺乏可靠性，且跟随数据集的不同在计算效率方面差别较大。

Vinagre 等人提出了一种基于正反馈的快速增量矩阵分解方法，通过随机梯度下降的方法来训练模型，并在增量过程中通过直接用增量数据逐条训练模型来提高效率，但是随着增量数据的累积，这种方法后期精度缺失较大。

Luo 等人提出了IR（incremental and static combined RMF-based recommender）算法。此算法可以适应大量的新数据并且能做出较准确的预测，但是在新数据进入后的预测过程中，抽取数据花费的时长较长，在时间方面有待于进一步提高效率。

Sun 等人采用正则化矩阵分解IncRMF（incremental recommendation algorithm based on regularized matrix）的方法，此算法虽将运算时间控制在较短范围内，但是在精度方面损失较大。

2 算法介绍

2.1 基础矩阵分解算法介绍

传统的矩阵分解算法是利用降维技术将用户-物品评分矩阵分解为两个低阶的矩阵，通过对这两个低阶矩阵的连续优化来减小预测值和真实值之间的误差，无限逼近原始评分数据，来达到预测用户-物品评分矩阵中未知评分的目的。定义用户-物品评分矩阵为∈R，特征维度为，用户特征矩阵为∈R，物品特征矩阵为∈R，矩阵的分解公式如下：

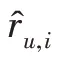
式中，e定义为真实值与预测值之间的误差，误差函数的公式如下：

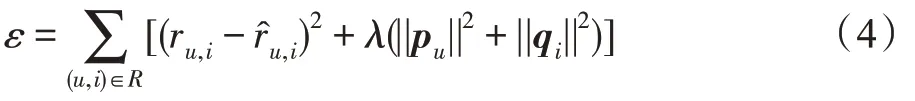
其中，||·||定义为标准欧几里德范数，代表正则化项，加入正则化项的目的是为了防止过度拟合所带来的误差。其中各参数的训练公式如下（p、q采用以下公式来进行更新）：

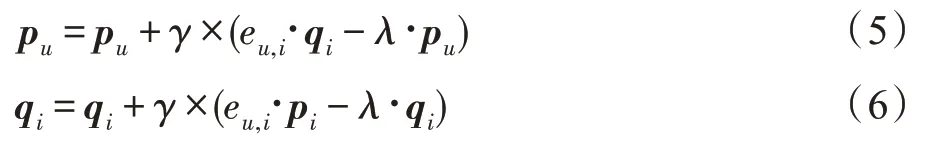
其中，代表学习的步长，其控制改变的速率，表示学习率。

2.2 增量式静态协同过滤推荐算法（Inc++算法）

本节基于IncRMF 算法提出了一种改进的增量式动静结合的协同过滤算法（improved incremental static combined collaborative filtering method，Inc++），该算法的目标是保证适应增量更新的效率要求且可以提供高度可靠的预测。下面将分四个小节介绍本文的算法。

在真实世界中，用户对物品的评分观念会受到周围环境或者自身性格改变的影响，不同性格的人群对相同的物品打分的标准也会有不同。例如：性格较乐观的用户通常对物品有较高的评分，性格较消极的用户通常对物品的打分较低。同时，物品本身也可能会受到广告效应等外界的影响从而导致评分发生改变。因此，考虑到外界因素的影响，在模型训练过程中融入了物品的偏置、用户的偏置以及全局偏置，分别定义为b、b、。其中，b为用户的偏执，是独立于物品的因素，表示的是某一特定用户的打分习惯，b为物品的偏执，是独立于用户兴趣的因素，表示某一特定物品得到的打分情况，为所有评分记录中的全局平均值，表示训练数据的总体情况。至此，模型中评分的预测公式为：

相应的用户偏执及物品偏执更新公式为：

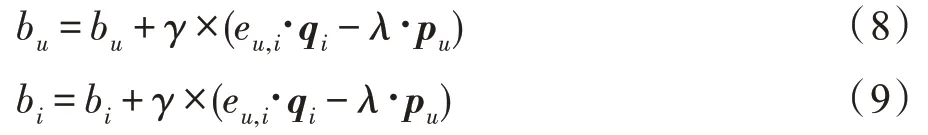
在数据更新过程中，随着每次增量数据的增加，用户和物品会在两个维度上增加，并在每次增量过程中，增量的用户数目和物品数目也会有所不同，为了可以在较短的时间内达到更新模型的目的，本文提出了分区域更新策略以更快计算用户特征和物品特征。如图1 所示，将新评分数据分为四个类别：A类评分，属于新用户、老物品的初始评分；B 类评分，属于老用户、新物品的初始评分；C 类评分，属于新用户、新物品的新评分；D 类评分，属于老用户、老物品的新评分。在初始训练阶段首先利用初始数据集进行训练，随着增量数据的不断加入，对增量数据进行单独训练，并非将所有的数据全部重新训练，相较于全部训练所有数据，此方法可以有效提高效率，节省时间。这里本文的增量策略将数据集中的用户集合划分为初始用户集合U和增量用户集合U，同样也将物品集合划分为初始物品集合I和增量物品集合I。其中：

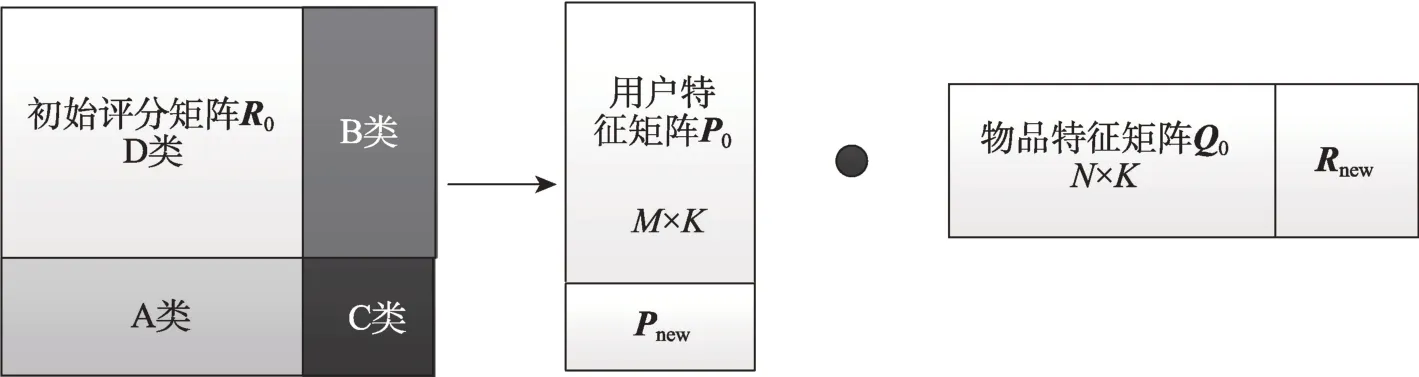
图1 分区域更新策略Fig.1 Regional update strategy

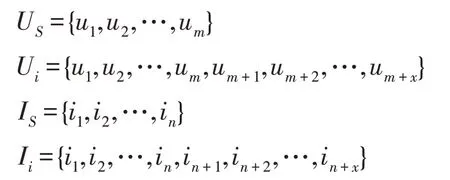
针对不同区域的新数据，在数据更新方面本文采用的更新策略也有所不同：

（1）当一个新评分属于A 类，即用户是新用户，在用户特征矩阵中添加新的特征向量p，并且利用前面的式（5）进行相应的训练。

（2）当一个新评分属于B 类，即用户是新物品，在物品特征矩阵中添加新的特征向量q，并且利用式（6）进行相应的训练。

（3）当一个新评分属于C 类，即用户是新用户且是新物品，分别在用户特征矩阵和物品特征矩阵中添加新的特征向量p和q，并且利用式（5）、式（6）进行相应的训练。

（4）当一个新评分属于D 类，即用户是老用户且是老物品，对其进行部分抽取得到相应的动态矩阵进行训练，具体的抽取过程在2.2.4 小节中进行介绍。

在对某一个用户或物品评分预测训练过程中，用户或物品的数据过于稀疏会导致数据预测的准确性降低，但评分的数据过多时，又会造成不必要的计算浪费。考虑到这点，本文在模型训练过程中，将用户和物品特征的最大训练次数设置了一定的阈值，定义为、。当某个用户或物品的训练次数到达阈值后，此用户或物品的相应特征便不再被训练，该阈值是一个超参数，由实验得到最优值，过滤机制的更多细节将在伪代码中进行介绍。

在迭代训练过程中，随着数据的实时进入，每个参数在训练过程中都会发生一定的改变，并且参数改变的影响是全局性的。在增量过程中，随着新数据的进入，为保证利用部分新数据来达到预测全局的目的，在提取动态评分矩阵时，针对不同的数据区域，采取不同的数据处理方法。首先对于新加入的评分，读取其相应的用户和物品id，在计算过程中通过初始评分矩阵上训练的用户和物品特征向量命名为p和q,在新数据进入过程中，抽取部分数据形成新的动态矩阵∈R，动态矩阵中的每一行代表一个新用户，每一列代表一个新物品。另外为了保证数据的相关性，将初始评分矩阵中和动态矩阵中有交叉的数据也放入动态矩阵中，这样在动态矩阵中，存在三种类型的数据：新加入的数据、初始评分数据、空值。在动态矩阵训练的用户和物品特征矩阵称之为p、q，在初始矩阵的用户和物品特征矩阵称之为p、q。提取动态矩阵如图2 所示。

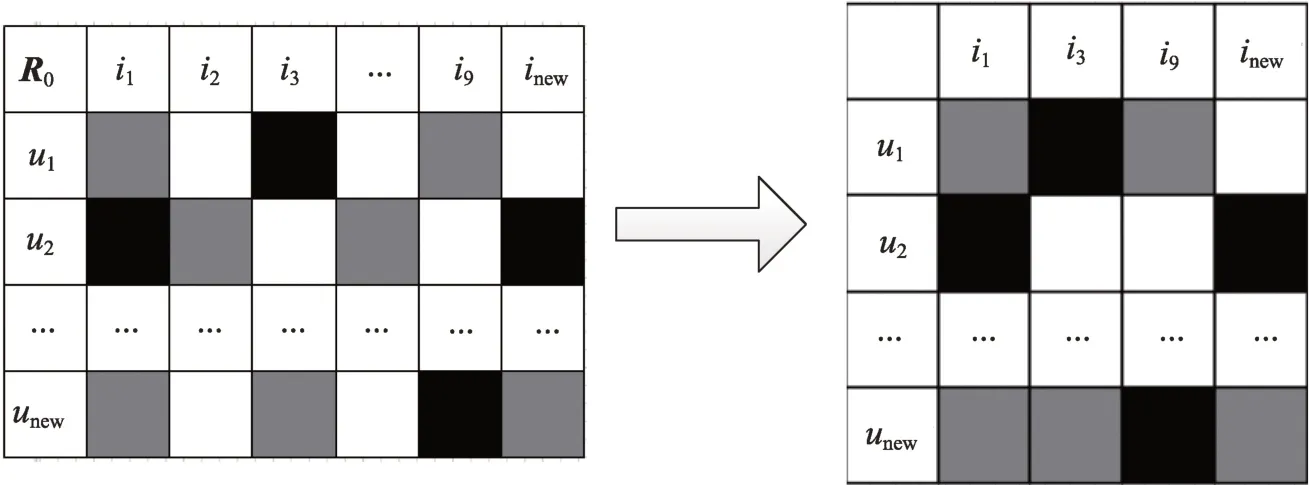
图2 提取动态矩阵Fig.2 Extracting dynamic matrix

对现有数据集中的有关数据进行提取之后，利用此矩阵进行数据训练，p、q、p、q训练公式如下：

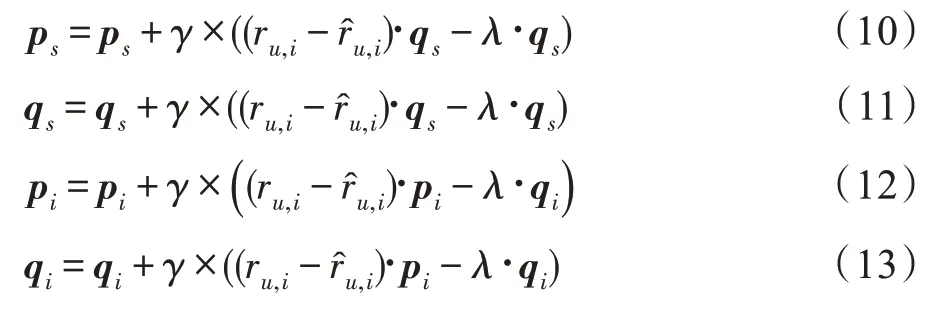
2.3 评分预测策略

本文将预测模块分为两部分，一个是初始训练的部分，一个是随着数据的进入的增量矩阵的预测部分，两部分评分预测公式为：

两个模块的结合预测权重由实验来确定。

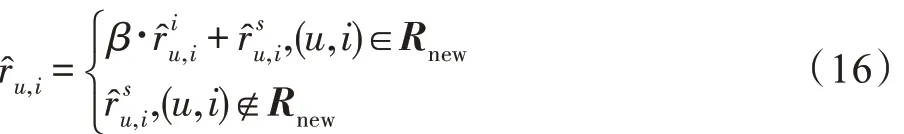
下面是Inc++算法的伪代码部分：

参数：、、_、_、、。

3 实验

3.1 实验数据集及设置

实验采用的数据集为Movielens-100K和Movielens-1M，其中Movielens-100K 包含943 个用户、1 682 个物品。Movielens-1M 包含6 040 个用户、3 952 个物品。将数据集乱序划分为三部分：初始数据集、增量数据集、测试集。初始数据集设置为整体数据的10%，测试集设置为整体数据的10%，增量数据集设置为整体数据的80%。用户和电影的特征维度设置为10，学习步长设置为0.02，学习率设置为0.3。Movielens-100K 数据集每次增量数据阈值设为500，Movielens-1M 数据集每次增量数据阈值为设为5 000，全局更新阈值设为50 000。评价标准为平方根误差，公式如下：

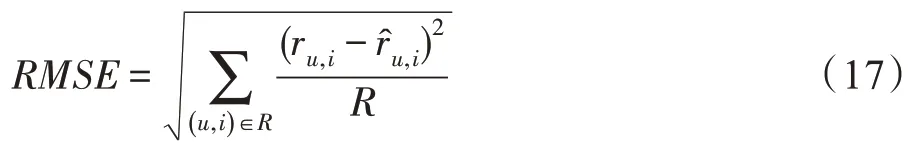
该算法将IR算法和IncRMF 算法的精度和时间值作为对比来进行对比实验。

本文的所有实验都是在同一硬件平台上进行的（Intel Core i5 CPU，8 GB 内存，Win10 64OS）。

3.2 实验结果及分析

不同的权重系数和用户、物品的更新阈值对实验结果的影响不同，为了突出主题，实验结果并没有在这里进行展示，经3 次随机实验测得当权重系数为0.4 和更新阈值为16 时RMSE 达到最优值，后续实验均在两者取最优值的情况下进行。

图3 和图4 分别显示了在数据集Movielens-100K和Movielens-1M 初始数据占10%的条件下RMSE 和时间对比实验结果。在两个数据集下，算法表现是相似的。首先在精度方面：从实验结果可看出，在初始阶段数据量较小时，Inc++算法具有良好的精度，这也表明该算法可以更好地适应冷启动过程。随着数据量的增加，IR算法和Inc++算法精度相差不大，精度差小于0.01，Inc 算法精度是表现最差的。但从时间方面可以看出，Inc 算法速度是最快的，Inc++算法比IR算法要快得多。

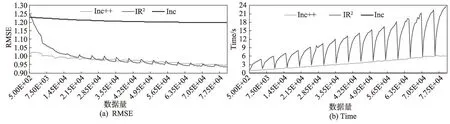
图3 RMSE 和Time对比（Movielens-100K）Fig.3 Comparison of RMSE and Time（Movielens-100K）

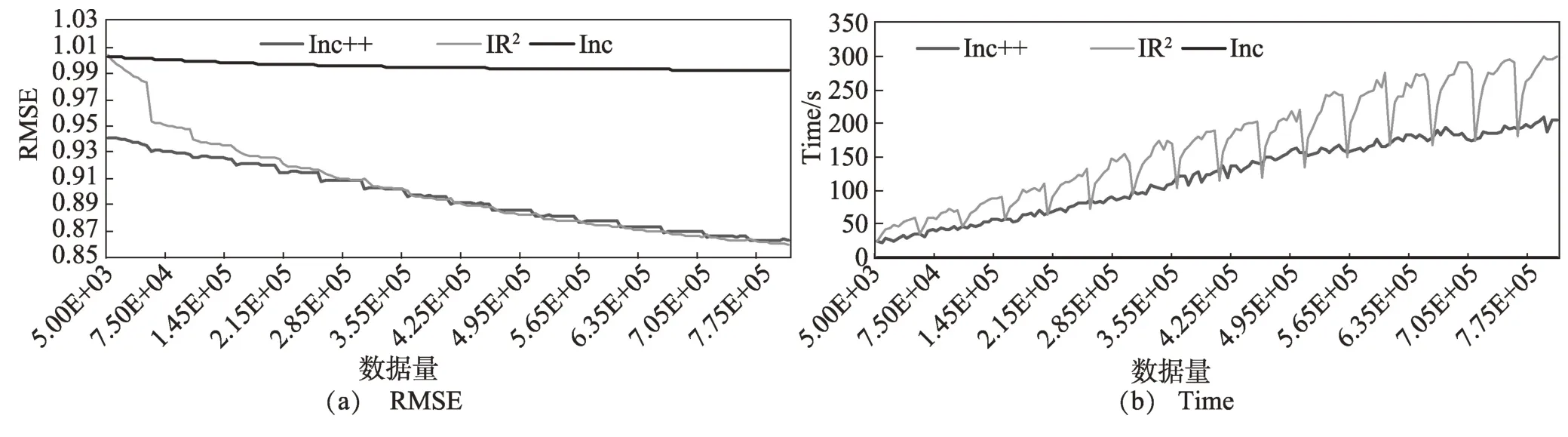
图4 RMSE 和Time对比（Movielens-1M）Fig.4 Comparison of RMSE and Time（Movielens-1M）

从实验结果综合分析可得：首先在精度方面，IR、Inc++这两个算法的精度高于Inc 算法，但在冷启动的情况下，Inc++算法能更好地发挥优势，较其他算法精度较高。其次在时间花销方面，Inc++算法在时间花销方面远远小于IR算法，相比于IR算法，Inc++由于每条新的特征训练都要达到拟合，在时间花销方面是较大的，Inc 算法只针对新的用户或新的物品，老用户、老物品不进行更新特征，因此精度的损失较大。Inc++集合了两个算法的优点，并且在训练过程中加入偏执信息，使得在时间方面比IR算法大大节省时间花销，但是相比Inc 算法精度又有了明显的提高，达到了较好的效果。

4 总结与展望

综合时间和精度两方面来说，Inc++算法表现最优。本研究的算法具有较好的准确度和实用性且总体时间花销较小，但是相比Inc 算法仍然在时间复杂度方面相差较明显。以后的工作方向将继续研究如何减少训练时间，提高算法训练的精度。其次，Inc++算法在数据量较小时表现优异，之后的研究也会针对冷启动这个问题继续深究。