构造直角三角形及其外接圆解决物理问题——从2022年全国乙卷理综第16题谈起

王栋然

(宁夏银川市第九中学)

高中物理习题常见以“圆形”为载体的情境,例如光滑圆轨道、半圆形玻璃砖等.巧妙利用圆形中蕴含的几何规律往往是行之有效的解题策略.在以“圆形”为情境载体的物理习题中,利用“直径所对应的圆周角为直角”这一规律来构造直角三角形是解决问题的常用方法.2022年全国乙卷理综第16题的解题方法就利用了该规律.

1 寻找距离关系

例1(2022年全国乙卷)固定于竖直平面内的光滑大圆环上套有一个小环,小环从大圆环顶端P点由静止开始自由下滑,在下滑过程中,小环的速率正比于( ).

A.它滑过的弧长

B.它下降的高度

C.它到P点的距离

D.它与P点连线扫过的面积

图1

解析本题考查的物理情境是竖直平面内的圆周运动,其依托的数学图形即为“圆形”.题目探究与小环速率成正比的物理量.本题是一道半定量问题,需要利用物理方程求解.求解小环的速率,应当选择动能定理.设小环下滑高度为h,则由动能定理得.可见,速率的平方与下降高度成正比.

那么速率与什么物理量成正比呢? 如图2所示,假设小环下滑到M点,作过P点的直径,交圆于另一点Q,设大圆环半径为R,则PQ＝2R.连 接MP、MQ,构 造Rt△MPQ,过M点作PQ的垂线,垂足为N.由题意得PN为下降高度h,PM为环到P点的距离d.

图2

因为△MPQ∽△NPM,所以

综上,在小球下滑过程中,小环的速率正比于它到P点的距离.答案为C.

2 探寻重力场中“等时圆”模型规律

高中物理中的“等时圆”模型的建立也利用了“直径所对应的圆周角为直角”这一规律.如图3-甲所示,A为竖直平面内的圆周顶点,B、C、D为圆周上的点,AE为直径.AB、AC、AD为三个光滑斜面.以AD为例进行研究,如图3-乙所示,设AD与AE间的夹角为α,连接DE,构造出Rt△ADE,则AD＝2Rcosα,物块在AD上由静止下滑时,有mgcosα＝ma,,与α无关,所以物块沿以A点为起点的光滑弦斜面下滑,时间相同.同理可证,在图3-丙中物体从光滑弦斜面DA、CA、BA下滑时间也是相等的.这就是重力场中的“等时圆”模型.在证明其等时性时需要构造直角三角形及其外接圆.

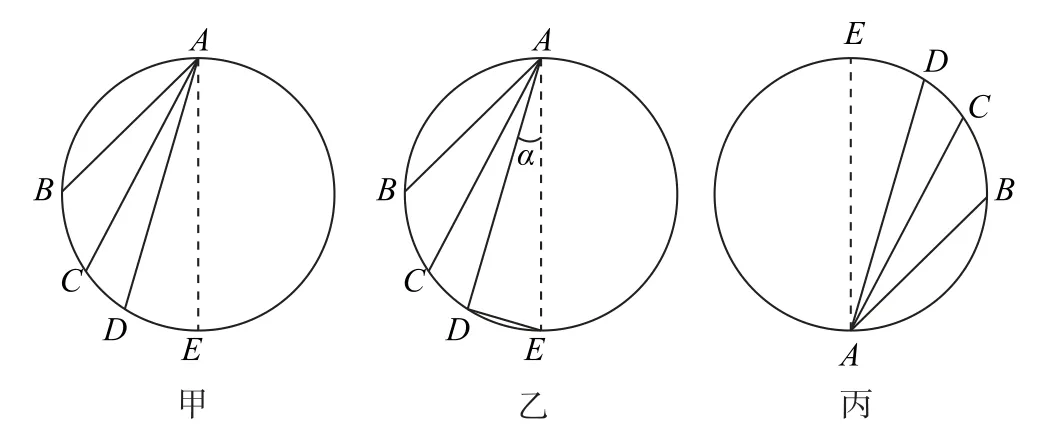
图3

例2如图4所示,AB和CD为两条光滑斜槽,它们各自的两个端点均分别位于半径为R和r的两个相切的圆上,且斜槽都通过切点P.设有一重物先后沿两个斜槽从静止出发,由A滑到B和由C滑到D,所用的时间分别为t1和t2,则t1与t2之比为( ).

图4

解析本题是“等时圆”模型的拓展与变形,可将“等时圆”模型的处理方法迁移过来.如图5 所示,选择AB斜槽展开研究,设过P点的直径分别交大、小圆于M、N点,AB与竖直方向夹角为α,连 接AM、BN,构 造Rt△AMP与Rt△BNP,则AB＝2Rcosα＋2rcosα,重物在AB槽由静止下滑时,有mgcosα＝ma,,联立解得,与α角无关,所以重物沿两个斜槽从静止出发下滑时间相等.答案为B.

图5

3 探寻惠更斯“等时圆”规律

如图6-甲所示,一束白光以入射角θ由空气射到半径为R的半圆形玻璃砖表面的A处,AB是半圆的直径,白光折射后色散的边界红光为AD,紫光为AC.选择红光进行研究,如图6-乙所示,连接BD,构造Rt△ADB,设红光的折射角为α,则红光的光程r＝AD＝2Rsinα,若玻璃砖对红光的折射率为n,根据折射定律有,红光在玻璃砖中的速度,光程r＝vt,联立解得.可见时间t是定值,与折射率无关,即色散后各色光到达玻璃砖圆弧面的时间相等.

图6

其实,上述结论也可用惠更斯原理证明(惠更斯原理:介质中任一波面上的各点,都可以看作发射子波的波源,其后任意时刻,这些子波在波前进方向的包络面就是新的波面).如图6-丙所示,过B点作A点入射光线的平行光线BB′,过A点作BB′垂线,垂足为M.由惠更斯原理可知,A与M点位于同一波面,介质中红光AD的D点与B点位于同一波面.紫光AC的C点也与B点处于同一波面,其他色光同理.所以无论是红光还是紫光或是其他色光,从A点传播到玻璃砖圆弧面的时间都等于白光在真空中从M点传播到B点的时间.我们将玻璃砖圆弧面所在的圆平面称为“惠更斯等时圆”.它的物理规律的探寻也同样需要构造三角形及其外接圆.

例3(2008年全国Ⅰ卷)一束由红、蓝两单色光组成的光线从一平板玻璃砖的上表面以入射角θ射入,穿过玻璃砖自下表面射出.已知该玻璃对红光的折射率为1.5,设红光与蓝光穿过玻璃砖所用的时间分别为t1和t2,则在θ从0°逐渐增大至90°的过程中( ).

A.t1始终大于t2

B.t1始终小于t2

C.t1先大于后小于t2

D.t1先小于后大于t2

解析本题如用解析法计算将非常复杂,但是利用惠更斯等时圆则可以巧妙解决.如图7所示,因为玻璃对红光的折射率为1.5,所以红光的最大折射角的正弦值,红光的最大折射角小于45°,蓝光的最大折射角必然小于45°.

如图7所示,构建惠更斯等时圆.从图中可见红光的实际光程小于与蓝光AL等时的光程AH,所以在平板玻璃砖中红光传播的时间始终小于蓝光传播的时间.答案为B.

图7

在以“圆形”为载体的物理情境中,“圆形”往往起着提供几何关系的作用,在解题时,不妨试着利用“直径所对应的圆周角是直角”这一规律,或许可以使解题更便捷.

(完)