基于深度学习的分布式光伏发电系统电压稳定性评估

吕晓洁

（中国国际工程咨询有限公司，北京 100048）

作为社会稳定发展的关键因素，电力系统的稳定关系到社会的发展。故准确评估电力系统的电压稳定性，对确保系统安全、提升电网经济效益等具有重要现实意义[1-2]。

该文以深度学习为技术支撑，设计分布式光伏发电系统电压稳定性评估方法。引入深度学习技术，建立系统运行状态特征量的映射关系，利用预训练与微调，不断更新模型参数，提升评估结果可靠性；合理设定光伏电池之间的距离，采用堆叠自动编码器，利于取得更完整且非冗余的数据特征，最终呈现精准的评估结果。

1 分布式光伏发电系统

1.1 分布式光伏发电系统结构

为实现分布式光伏发电系统电压稳定性评估，首先分析分布式光伏发电系统的结构。采用光伏电池组、汇流箱、微网逆变器等组件，构建分布式光伏发电系统[3]，如图1 所示。

将该系统中晶硅电池与薄膜电池光伏组件串联装于建筑物顶部，将接收的太阳辐射能量转换为电能；利用微网逆变器[4]实现直流电到交流电的转换，用户所用电能主要由交流配电装置提供。

假设研究区域位于φ纬度，且电能电池组阵列前排最高点与后排最低点之间相差高度为H，则设定光伏电池之间的距离为d[5-6]，如式（1）所示：

1.2 分布式光伏发电系统电压变化

为准确评估分布式光伏发电系统电压稳定性，基于发电系统接入低压配电网的等效电路，对发电系统电压变化原因进行深入探索。

已知并网点电压为U，并网点负荷为PL+jQL，配电网的等值电压与等值阻抗分别为Us、R+jX，光伏电源发出功率为P+jQ，接入配电网功率为Ps+jQs，根据光伏电源发出功率与接入配电网功率相关性[7]，得到：

若U0为并网点在发电系统并网之前的电压，则：

低压配电网与高压系统交互性较弱，网架较为简易，且免疫性相对偏低，无法进行带载调压，故导致低压配电网等值电压发生波动[8]。

光伏发电系统通过对配电网重载过程中电网的功率进行支持，缓解配电网产生的负荷压力，若配电网处于轻载阶段，发电系统呈高出力状态[9]，则发生过电压问题的概率较高。因此，采用式（4）描述因光伏接入而形成的并网点电压幅值ΔU。

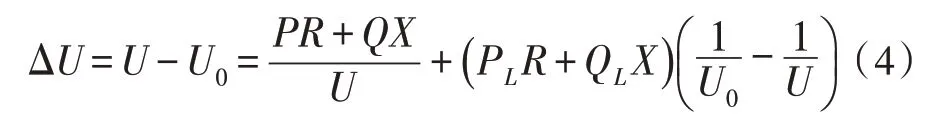
根据该近似式可以看出，配电网的接入是导致分布式光伏发电系统电压发生变化的主要诱因。

2 自动编码器下分布式光伏发电系统电压稳定性评估

2.1 电压稳定性评估模式

基于所建分布式光伏发电系统，通过特征提取与分类评估两个阶段，设计该系统电压稳定性评估模式，如图2 所示。

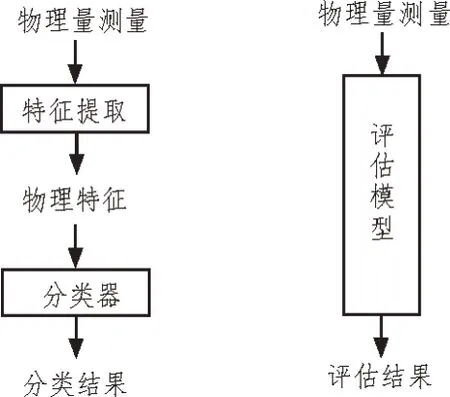
图2 电压稳定性评估模式

图2 中，左侧提取的特征组成部分通常为负荷水平、电压水平等物理量，可由光伏发电系统的物理量测量解得。

由于提取特征缺乏全面描述实际问题的能力，仅能体现发电系统的局部特征，在一定程度上限制了电压稳定性评估准确度，故需要整合特征提取与分类评估两个阶段，从根本上实现数据特征的自动挖掘与分类评估[10]。该评估模式令物理量测量与分类结果之间建立直接映射关系，确保信息的完整度。

2.2 基于堆叠自动编码器的深度学习算法

针对上述分析的分布式光伏发电系统结构，由于多种因素的干扰，导致系统电压发生一定变化。为了快速确定发电系统的电压，该文借助深度学习算法[11]对其稳定性进行评估。

深度学习算法中利用输入层、输出层以及隐含层构建图3 所示的自动编码器AE（Auto Encoder）。

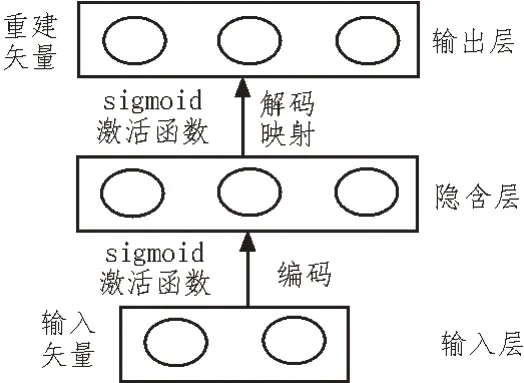
图3 自动编码器框架

该编码器是一个对称神经网络，采用编码与解码流程，最小化输入信息的重建偏差，取得最优隐层表征。通过该技术原理，将影响电力系统电压稳定性的参数进行最优隐层表征[12]，以确定电压系统的稳定性。

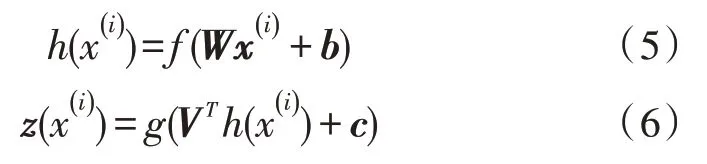
式中，sigmoid 激活函数分别用f、g表示。

当输入的电力系统电压参数重建偏差L(x，z)较小时，编码矩阵才具有初始信息特征，需要通过训练数据集搜寻自动编码器的最佳参数θ′，实现重建偏差L(x，z)最小化处理[13]，即：

训练集中隐藏层第j个神经元的激活水平由下列平均激活量界定[14]，即：

在上述分析基础上，采用稀疏性约束的目标函数，求解最优自动编码器参数，即求取分布式光伏发电系统电压干扰参数θ′，如式（9）所示：

式中，稀疏惩罚项权值为γ，隐藏层单元数量为HD。

以取得具备完整性的非冗余电压数据特征为目标，将自动编码器堆叠，形成深层神经网络模型，完成堆叠自动编码器架构。将编码器下层输出项设置为上层输入项，经堆叠得到关联电力系统电压的有效特征。

堆叠自动编码器数据预训练过程分别为预训练与微调，如图4 所示。

图4 堆叠自动编码器预训练图

当从下至上预训练一个l层的堆叠自动编码器时，需将训练样本作为输入项训练第一层，再将第k个隐藏层输出作为输入项训练第k+1 个隐藏层，完成各层预训练。对于编码矩阵W与偏置向量b，利用梯度下降法[15]进行循环计算，并通过下列方程式更新神经网络的第k层：

式中，学习率为ε。

基于底层量测数据r，利用设计堆叠自动编码器与softmax 回归层分类器，架构电压稳定性评估模型，如图5 所示。

图5 电压稳定性评估模型

该模型通过描述底层量测数据与稳定种类间的非线性映射关系，实现电压稳定性评估。利用模型基础部分（即堆叠自动编码器）分层表达分布式光伏发电系统信息，获得有效性特征，采用位于模型最上层的分类器，通过softmax 回归层划分和输出样本稳定种类[16]。假设样本存在n种稳定种类，则softmax回归层的隐含函数关系为：

式中，网络顶层下一层的输出矢量为x，该网络层与第一个、第二个输出单元的权值矢量分别为θ1、θ2。

在训练电压稳定性评估模型过程中，根据无标注训练数据集T1={r}1与有标注训练数据集完成相关训练参数的设定；利用T1进行堆叠自动编码器的预训练；采用T2按以下两个步骤微调模型参数：

2）利用梯度下降算法，从上至下对模型参数展开监督优化。

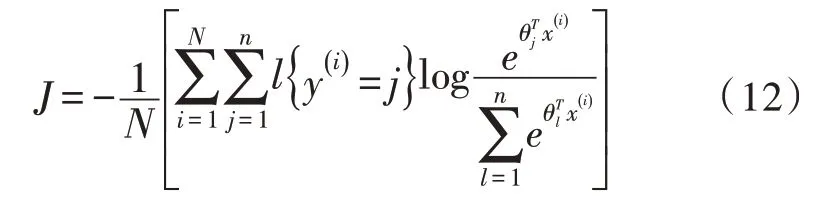
通过梯度下降算法寻优处理代价函数，权重随迭代更新，完成评估模型参数的微调，实现电压稳定性评估。

3 实验分析

3.1 实验环境

按照表1 所示配置参数搭建实验平台和训练样本数据集，进行实验分析。评估模型最优参数如表2所示。

表1 实验环境相关配置参数

表2 评估模型最优参数

在上述实验环境和参数设定下，该文为了验证分布式光伏发电系统电压稳定性，根据发电系统负荷母线电压实际变化情况以及电压稳定性评估模型对电压稳定性进行评估。

3.2 实验结果分析

令该文分布式光伏发电系统的运行负荷约等于额定电压，其光照强度为800 W/m2，温度为26 ℃，单相额定有功功率为0.22 MW，当发电系统进入平稳的运行状态，其负荷电压达218.3 V。通过降低光照强度、提升环境温度以及发生瞬时性单相接地短路的方式，验证评估模型的免疫性，发电系统负荷母线电压实际变化情况如图6 所示。电压稳定性评估模型仿真结果如图7 所示。

图6 发电系统负荷母线电压实际变化情况

图7 电压稳定性评估模型仿真结果

根据图6 中负荷电压实际情况可知，光照与温度因素均未导致发电系统的负荷母线发生电压失稳状况，电压较为稳定，而短路故障因素使母线电压迅速下跌，直到故障消失，电压未恢复至故障发生前水平，说明短路故障造成电压失稳；将实际电压情况与该文方法判据指数结果（见图7）作对比后可以看出，该文方法准确评估了分布式光伏发电系统的电压稳定状况，这是由于所提方法有效融合了特征提取与分类评估，利用基于无监督深度学习的堆叠自动编码器，挖掘出样本数据集的规律与特征，获取更完整且非冗余的数据特征。

4 结论

能耗与污染问题日益严峻，为大力落实可持续发展战略目标，发挥太阳能发电优势，分布式光伏发电系统逐渐演变成未来能源领域的重要角色之一。分布式光伏发电系统项目已初见雏形，其并网技术更是在与电网的有效结合中起着关键作用，但随之而来的电压波动成为需重点解决的问题。因此，该文结合深度学习技术，构建出一种分布式光伏发电系统电压稳定性评估方法。该方法通过对分布式光伏发电系统电压变化的分析，结合深度学习算法实现了其稳定性的评估，具有一定的可行性。