旋翼飞行器抗风扰控制器设计与风场环境建模

黄梦渊，王耀力，张祉怡，常 青

（1.太原理工大学信息与计算机学院，山西太原 030024；2.北京师范大学 人工智能学院，北京 100875）

无人机广泛应用在铁路检测[1-3]、快递包裹[4-5]等多个领域。室外风场存在会影响飞行器的飞行姿态和稳定控制性能。使用飞行器实物验证控制器抗风干扰效果时，容易出现失控，产生危险，增加飞行器研究成本。

国内外学者对相关内容进行了广泛研究。文献[6]采用LabVIEW 仿真软件来显示飞行器的飞行姿态，但无法模拟风场环境。文献[7-12]采用EKF滤波对风环境中的飞行器姿态进行实时估计，但抗风干扰能力差。

该文主要研究风场环境下的旋翼动力学模型；设计双自适应衰减扩展卡尔曼滤波算法(Dual Adaptive Fading Extended Kalman Filter，DAFEKF)来提高姿态数据的滤波精度，并结合PID 控制器来增强系统的抗风干扰能力；对室外风场环境进行分析，建立3D风场仿真模型，进一步验证系统的控制效果。

1 风场模型

在自然界中往往存在着多种类型的风，通常有平均风、风切变、紊流风、阵风等。但四旋翼飞行器在室外飞行时，通常作用在四旋翼上的主要是紊流风和阵风。对于紊流风，一般用Dryden 模型来产生紊流风。将高斯白噪声序列通过成形滤波器形成有色噪声序列，实现对大气紊流的建模。

Dryden 模型的时间频谱表示为[13]：

其中，σμ、σv、σω分别表示纵轴、横轴和竖轴方向的紊流强度，Lμ、Lv、Lω分别表示三轴方向的紊流尺度，v代表旋翼飞行器的飞行速度。由于旋翼飞行器一般都在低空飞行，则依据8785C 规定，紊流强度和紊流尺度可用以下公式得出[13]：

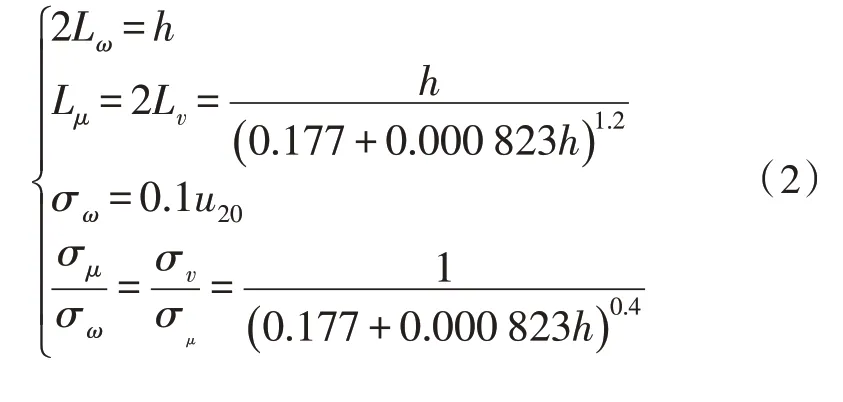
其中，h代表飞行器的飞行高度；u20代表高度为6.096 m 的风速大小。

将单位强度的白噪声序列通过一个强度为G(s)的成形滤波器，产生的输出序列的频谱函数为：

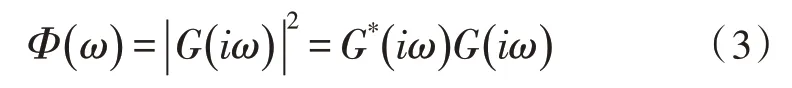
其中，*代表共轭。根据式（3）对式（1）进行分解，可以得到成形滤波器的传递函数为[13]:

离散突风是指在各个方向上出现忽大忽小的风，又称阵风。通常用半波离散突风模型表示[14]，如式（1）：

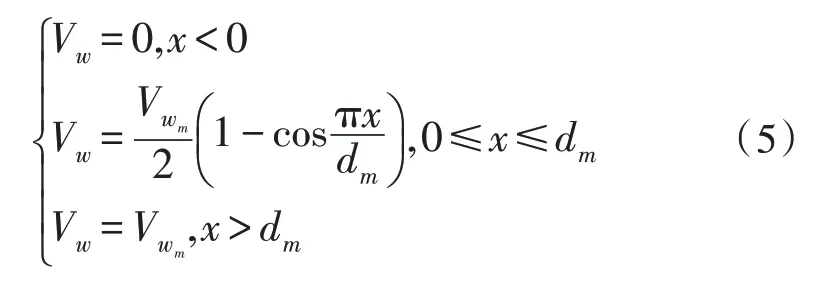
其中，dm为阵风尺度范围，为阵风峰值，x为距离阵风中心的距离。

将紊流风和阵风相结合可得到真实风场环境，如式（6）：

2 风场中的旋翼动力学模型

2.1 坐标系的建立

四旋翼飞行器在风场环境下进行动力学建模时，首先建立相应的坐标系。该文采取了惯性坐标系O3X3Y3Z3、机体坐标系O2X2Y2Z2、气流坐标系O1X1Y1Z1。X轴为四旋翼的飞行速度方向，Y轴由右手定则确定，Z轴垂直水平面向上。姿态角度θ、Ψ、φ为俯仰角、偏航角、滚转角。气流角α、β为仰角、侧滑角。

2.2 动力学建模

通过对四旋翼运动过程分析可知，四旋翼运动状态一般分为平移运动和转动运动。因此，采用Newton-Euler 法对风场环境下的四旋翼的平移运动和转动运动进行建模。

由空气动力学可知四旋翼所受风场阻力为[15]：

其中，CW为风场阻力系数，S为机身的有效面积，Vm为惯性坐标系下的风速大小。

因此，风场环境下四旋翼的平移运动和转动运动方程为：

其中，k为升力系数，kd为阻力，Ω为电机转速。

3 DAFEKF算法设计

在室外，由于风干扰因素的存在，要实现四旋翼的稳定飞行，就必须及时地获取飞行器的位置和姿态信息。通过IMU 获取的姿态数据具有大量噪声，而EKF 滤波具有除去噪声和对姿态进行实时估计的功能。但EKF 也存在缺陷，需要对其进行改进。

3.1 EKF算法

四旋翼飞行器的非线性系统[16]如式（10）：

其中，Xk和Zk分别代表系统状态量和观测量；f(·) 和h(·) 代表非线性函数；B为控制输入矩阵；wk-1和vk分别代表过程噪声和测量噪声。

根据EKF 理论可知，EKF 滤波算法[17]具体实现过程如下：

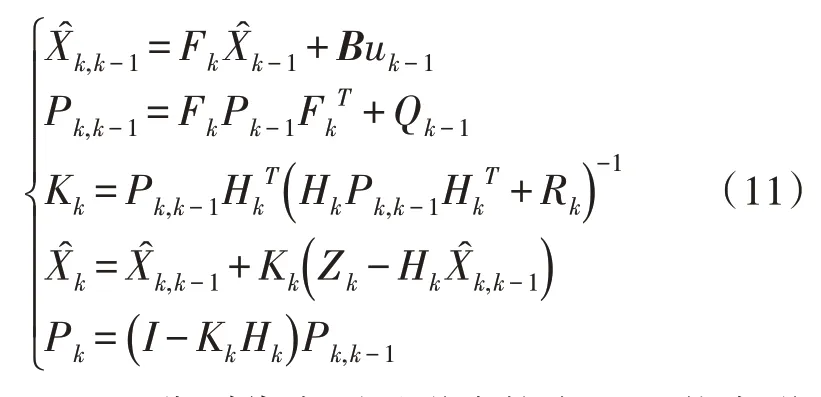
其中，R和Q分别代表测量噪声协方差和状态噪声协方差。

在扩展卡尔曼滤波算法中，不仅存在目前滤波数据对历史数据的过度依赖问题，而且R和Q通常为固定值。但是，四旋翼在室外飞行时，由于风场的影响，测量噪声和状态噪声通常并不是固定值，这使得EKF 算法的滤波精度变低，抗风干扰能力变差。因此，设计了DAFEKF 算法。

3.2 DAFEKF算法

DAFEKF 算法不仅设计了自适应衰减因子，利用该因子来减小历史数据对目前滤波数据的影响，同时，添加自适应因子来不断对当前的Q和R进行调整，改善滤波精度，提高抗风干扰能力。

由EKF 理论可知，采用新息序列来描述实际测量值与预测测量值之间的误差协方差[18]如式（12）：

对R提取的自适应因子为：

对Q提取的自适应因子为：

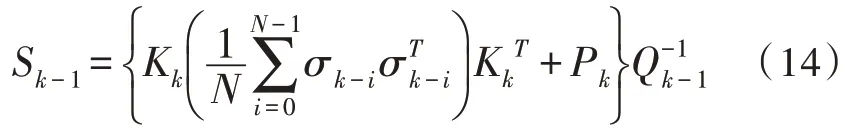
设计的自适应衰减因子λk如下：

4 算法验证与分析

该文分别对风场和风环境下的四旋翼动力学进行建模，设计了DAFEKF 滤波算法的状态估计器，并与PID 控制器相结合。将建立的风场模型应用到四旋翼系统，通过MATLAB/Simulink 对整个系统进行建模。

设置四旋翼飞行器的初始位置X=[0 0 0]，期望位置X=[6 6 15]，初始姿态角η=[0 0 0]，期望姿态角η=[0 0 0.5]，风速为5 m/s。将新设计的带有自适应因子的R和Q以及自适应衰减因子λk的PID-DAFEKF 控制系统与经典的R和Q为固定值的PID-EKF 控制系统，以及鲁棒性强的滑模控制系统对风场环境中四旋翼实现定点悬停的控制效果进行对比。设置时间为30 s，对比结果如图1 和图2所示。

图1 三轴位移输出曲线和三轴位移绝对误差值

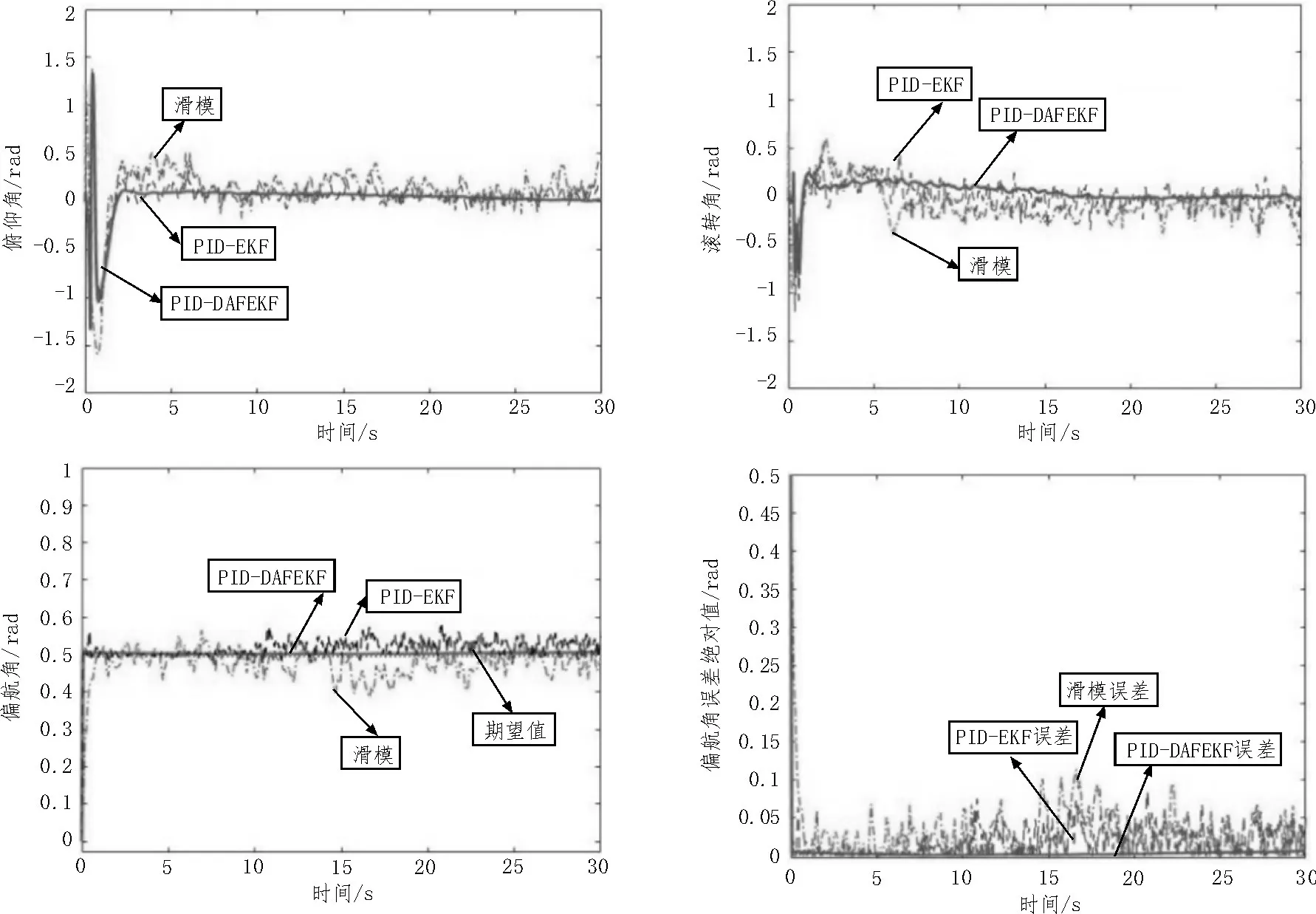
图2 姿态角输出曲线和偏航角误差绝对值

由图1 可知，在风场环境中，分别给四旋翼3 个方向设定期望值，并使用3 种不同的控制方式来实现四旋翼的定点悬停和抗风干扰控制。采用滑模控制算法后，三轴位移的最大绝对误差分别约为0.58 m、0.59 m、0.81 m。虽然滑模有较强的鲁棒性，但未对姿态数据进行估计。并且，由于风场的不断扰动，使得滑模产生的抖动比较大，抗风干扰能力差。采用PID-EKF 算法后，不仅对飞行器姿态进行实时估计，还对姿态数据进行滤波处理，使得三轴位移的最大绝对误差分别约为0.2 m、0.32 m、0.45 m。误差相对减小，响应速度变快。采用PID-DAFEKF 算法后，对测量噪声和状态噪声不断在线更新，并引入自适应衰减因子，减少当前滤波值对陈旧数据的过渡依赖，使得三轴位移的最大绝对误差分别约为0.05 m、0.06 m、0.06 m。提高了滤波精度，抗风干扰能力更强，使飞行器的悬停更加稳定，更加接近期望值。

由图2 可知，在风场环境中，设定期望偏航角为0.5 rad。采用滑模控制算法后，X轴和Y轴方向上的位移抖动性比较大，使得俯仰角和滚转角的波动比较大，飞行器稳定性差，同时，偏航角也产生了较大误差，最大绝对误差值约为0.12 rad。采用PID-EKF算法后，对飞行器的姿态进行估计，并对姿态数据进行了滤波处理，使得俯仰角和滚转角的波动减小，也使得偏航角的误差减小，最大误差绝对值约为0.1 rad。最后，采用新设计的PID-DAFEKF 算法后，对测量噪声和状态噪声不断在线更新，并引入自适应衰减因子，使得姿态估计更加准确，滤波效果更好，偏航角的输出更加接近期望值，最大绝对误差几乎为零。整体抗干扰能力好。位移与偏航角均方根误差统计如表1 所示。

表1 位移与偏航角均方根误差统计

由表1 可知，在风场环境下，采用滑模控制器后，位移与偏航角分别与期望值产生一定偏差。当使用PID-EKF 算法对飞行器姿态进行估计以及对姿态数据进行滤波后，使得RMSE 分别减少了49%、55.7%、49.2%、52.8%。通过新设计的PID-DAFEKF算法对EKF改进后，RMSE分别减少了81.2%、82.7%、84.6%、83.2%，其使飞行器的稳定性更好，抗风干扰能力更强。

5 平台仿真

在前面使用MATLAB/Simulink 对新设计算法的可行性进行验证，结果表明，该算法的抗风干扰效果好，为了进一步验证该算法的合理性、有效性和可视化四旋翼飞行器在风场环境中的稳定性，一般采用飞行器实物进行抗风干扰实验，但容易出现失控、坠机等现象，增加飞行器研究成本。因此，在开源仿真平台建立3D 风场环境模型来实现四旋翼在仿真平台的风环境中进行抗风干扰测试，代替使用四旋翼实物进行抗风干扰测试。实现四旋翼在风场中飞行姿态的可视化，降低飞行器研究成本。

5.1 3D风环境建模

该文采用Gazebo 三维动态仿真平台，模拟复杂的室内外环境、机器人和飞行器。根据前面建立的风场数学模型，在Gazebo 仿真平台的世界模型中建立风世界，将Gazebo 仿真平台中的空世界转变成风世界。并通过mavros 和mavlink 来实现Gazebo 仿真平台与飞控平台相连通。在Gazebo 仿真平台模拟的风环境中，使用编写的Ros 代码对四旋翼进行目标位置设置，为X=[6 6 15]，并利用飞控平台的外部控制模式来控制Gazebo 仿真平台中的四旋翼，实现定点悬停。使四旋翼飞行器在风场环境中的稳定性和飞行姿态可视化。在风世界模型中分别对X轴和Y轴方向设置风速为5 m/s 的风场。定点悬停流程图如图3 所示，在X轴和Y轴风场环境下的姿态角如图4 所示。

图3 定点悬停流程图

图4 风场环境中的姿态角

图3 流程图显示了通过Ros 代码实现Gazebo 中的四旋翼的定点悬停控制。

由图4 可知，在Gazebo 中首先引入沿X轴方向的风场，仿真平台中的四旋翼在俯仰方向产生倾斜，并不断抖动，俯仰角在0.15 rad 附近不断变化。然后引入沿Y轴方向的风场，仿真平台中的四旋翼在滚转方向产生倾斜，并不断抖动，滚转角在0.17 rad 附近不断变化。

5.2 轨迹跟踪

完成Gazebo 仿真平台中风世界的建立，并与飞控平台相连通之后，通过QGC 地面站设置航点位置及航点任务，进行航迹规划。在mission 模式下启动四旋翼飞行器，使四旋翼飞行器在风场环境中进行轨迹跟踪，结果如图5 所示。

图5 轨迹跟踪

在Gazebo仿真平台的风世界中，引入风速为5 m/s的风场，设置飞行高度为15 m，并启动仿真平台中的四旋翼在风场环境中进行航迹跟踪。分析飞行器的飞行日志，由图5 仿真结果可知，由于风场干扰，飞行器在3D 风场环境下的实际飞行轨迹与期望轨迹产生偏离。旋翼飞行器在俯仰方向和滚转方向产生倾斜并不断抖动；经过新设计的PID-DAFEKF 滤波算法处理后，在风场环境中，飞行器的实际飞行轨迹与期望飞行轨迹相吻合，轨迹跟踪结果精确，四旋翼飞行器在风场环境中能稳定飞行，具有良好的抗风干扰能力和跟踪效果。

6 结束语

根据四旋翼飞行器在室外飞行时所受的风场干扰，设计了PID 位置控制器与DAFEKF 滤波算法相结合的控制系统。在开源仿真平台中建立3D 风场环境模型，实现通过仿真平台中的风环境来验证抗风干扰算法的有效性。实验结果显示，设计的控制系统不仅具有很好的抗风干扰能力，而且开源仿真平台建立的3D 风场环境能很好模拟飞行器在室外飞行时所受到的风场干扰。