基于二维MUSIC 算法的干扰信号来向估计FPGA 实现

任婵婵，陈 静，陈耀辉，祝娇娇，刘盛典

（1.天津航天中为数据系统科技有限公司，天津 300462；2.航天恒星科技有限公司，北京 102209）

卫星导航信号的脆弱性使得导航接收设备极易受到人为和自然等干扰而无法正常工作。干扰信号来向估计能够快速地定位干扰信号入射角度，然后根据干扰位置自适应地改变方向图中的零陷方向，使导航抗干扰接收机在干扰方向形成零陷准确的抑制干扰[1]。文献[2]提出的扩展波达方向(Direction of Arrival，DOA）矩阵算法解决了线性阵列的窄带信号到达方向估计问题，该算法通过构造扩展DOA 矩阵的特征值与特征向量计算得到DOA 估计结果，所提方法性能优于传统的DOA 矩阵方法。文献[3]研究了一种基于联合奇异值分解(Joint Singular Value Decomposition，JSVD)的快速、鲁棒的互素阵列DOA估计方法。该方法首先根据互素阵列的几何形状，将互素数组等效地分为两个均匀的稀疏线性子数组。然后，利用JSVD 算法和均匀稀疏线性阵列的周期可重复性，每个子阵列可分别获得两组DOA，分析这两组DOA，可以根据互素数组的两个等效均匀稀疏线性子数组的互素属性，得到正确的DOA。文献[2]和文献[3]所提出的算法均用于信号来向估计，但算法的模型构造均较为复杂。文献[4]针对带有互质线性阵列的DOA 估计问题，提出了一种基于多重求根MUSIC 的DOA 改进算法，该算法充分利用信号空间和噪声空间，以较低的复杂度提高了角度估计精度。文献[5]针对复杂电磁环境下相干信号源的DOA 估计问题，研究了一种基于空间平滑的改进MUSIC 算法，分别给出了在不同快拍数和不同信噪比条件下，该算法与传统MUSIC 算法对相干信号的DOA 估计性能仿真，基于空间平滑改进的MUSIC 算法能有效改善对相干信号源的测量性能。文献[4]和文献[5]均是涉及一维角度的基于MUSIC 及其改进算法的信号来向估计问题。文献[6]在利用二维MUSIC 算法进行信号到达方向估计的过程中对算法进行了降维处理，提出的算法仅需一维搜索，就可以有效地避免二维MUSIC 算法的高计算量，但该算法不能估计信号数量。文献[7]将球形麦克风阵列应用于DOA 估计，构造了球谐函数与傅里叶级数之间的映射矩阵，然后利用傅里叶级数的范德蒙德结构得到了多项式求根方法，利用傅立叶级数的特征，可以构造两个根多项式，来分别估计方位角和俯仰角，所提出的方法将二维MUSIC 算法中的角度搜索转换为了两个一维角度求解。文献[6]和文献[7]对二维MUSIC 算法进行DOA 估计时做了降资源处理，但都只停留在理论研究阶段，均未进行实际应用的讨论。

该文以阵列信号抗干扰为背景，针对干扰信号的来向角度估计问题建立了二维MUSIC 算法模型。首先，给出二维MUSIC 算法的实现步骤，其次，推导了该算法中的特征值分解、空间谱计算和谱峰搜索模块的具体计算方式和流程，并给出了具体的FPGA实现方式。实验与仿真表明，所实现的算法能够预估干扰信号的个数和入射方向。

1 二维MUSIC算法

1.1 算法模型

空间中有远场信号入射到天线阵上，信源个数为K，二维入射角为(θk，φk)，k=1，2，…，K，其中，θk、φk分别代表第k个信源的俯仰角和方位角。则M个阵元接收到的信号可表示为:

其中，S为接收信号，N为接收噪声，A为导向矢量。

根据接收到的信号得到信号协方差矩阵为:

其中，L为快拍数。

对协方差矩阵进行特征值分解，得到特征值V矢量和特征向量矩阵D，对特征值V矢量中的元素进行由大到小的排序，设定合理阈值EV，V矢量中大于等于EV值的个数则为入射信号个数。

利用小于阈值EV的特征值对应的特征向量张成噪声子空间UN，根据如下公式构成空间谱函数:

设定合理阈值EN，对空间谱函数进行二维搜索，当P2D-MUSIC()θ，φ≥EN时，记录该谱峰的位置，根据谱峰的位置可估计入射信号的角度信息。

1.2 实现步骤

二维MUSIC 算法实现步骤如下：

1）根据接收信号求得信号的协方差矩阵，并对协方差矩阵进行特征值分解，分别得到特征值和特征向量；

2）设置合理阈值，根据特征值与阈值比较，特征值大于阈值的个数判定为入射信号的个数；

3）根据特征向量构造噪声子空间，根据导向矢量和噪声子空间得到空间谱函数；

4）设定阈值，对空间谱函数进行二维峰值搜索，根据谱峰可估计入射信号的角度。

2 算法FPGA实现

2.1 特征值分解

接收信号的协方差矩阵一般为复数Hermite 矩阵，M阶Hermite 矩阵Rxx可分解为:

其中，A为Rxx中的实数组成的矩阵，B为Rxx中的虚数组成的矩阵。Hermite 矩阵Rxx满足Rxx=RxxH，可得AT=A，BT=-B。设特征值为λ，对应的特征向量为U+iV，其中，U、V均为M阶的实数列向量，则有:

上式可写为:

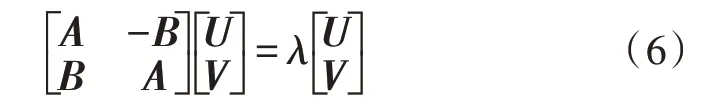
可见求复数协方差矩阵Rxx的特征值和特征向量问题可转化为求实数协方差矩阵的特征值和特征向量问题。

对实数协方差矩阵的特征值分解过程采用Jacobi 算法来实现，文献[8]对该部分内容进行了详细阐述，可查阅相关文章，这里不再赘述。

2.2 空间谱计算

将特征值分解模块得到的特征值和特征向量作为空间谱计算模块的输入，假设阵元数为M。空间谱计算处理流程如图1 所示。

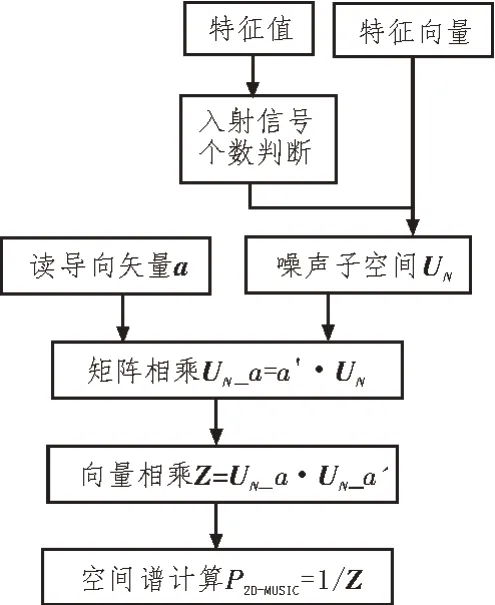
图1 空间谱计算处理流程

2.2.1 入射信号个数判断

接收信号的协方差矩阵经过特征值分解后得到特征值和特征向量。其中，特征值按照由大到小的顺序排序，所有特征值对应的特征向量组成M×M的矩阵，特征向量的顺序与特征值一一对应。设定合理阈值EV，将特征值向量中的元素依次与阈值EV进行比较，所得的特征值大于阈值的个数用J表示，并将该参数用于噪声子空间生成。

2.2.2 噪声子空间生成

噪声子空间模块接收到有效的特征向量后开始计数，将数据记为J，然后开始锁存特征向量，将锁存的M-J个特征向量生成噪声子空间UN，记为：

2.2.3 导向矢量读取

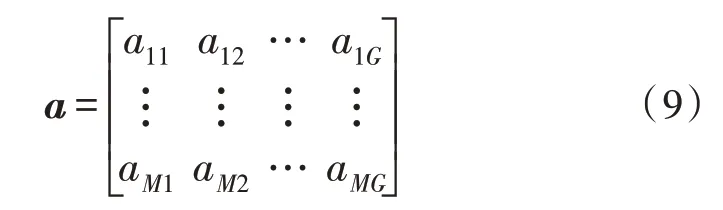
读取存储的第一频点归一化后的导向矢量a，导向矢量个数如式（8）所示：

其中，Po表示方位角精度，Pp表示俯仰角精度。因此，导向矢量a的维度为M×G，记为：

2.2.4 矩阵相乘

矩阵相乘模块完成噪声子空间UN和导向矢量a的乘法运算，对相乘的结果进行存储，相乘运算过程如下:

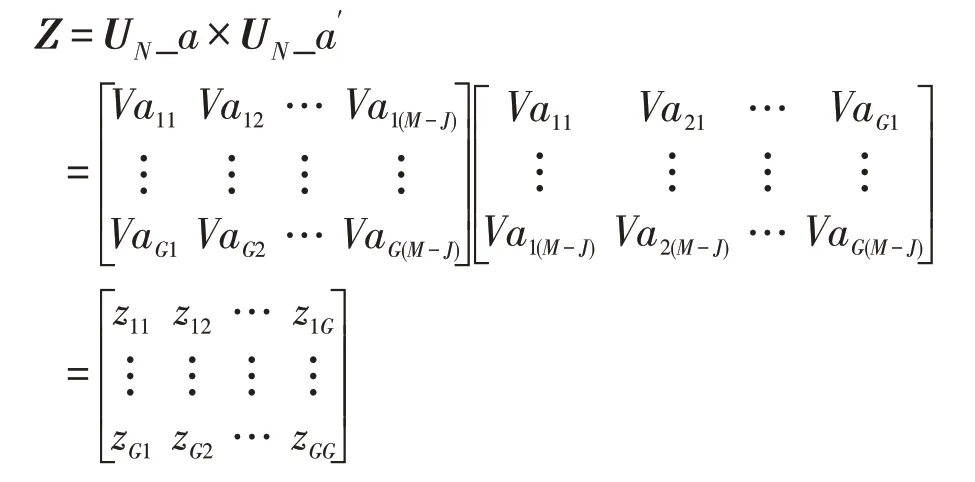
2.2.5 向量相乘

提取存储的矩阵相乘结果UN_a，对该结果进行向量相乘，相乘过程如下所示。

2.2.6 空间谱计算

空间谱计算主要是进行除法操作，其过程如下：

2.3 谱峰搜索

谱峰搜索模块主要完成对空间谱的峰值搜索，定位峰值位置，得到信号估计角度。谱峰搜索模块处理流程如图2 所示。

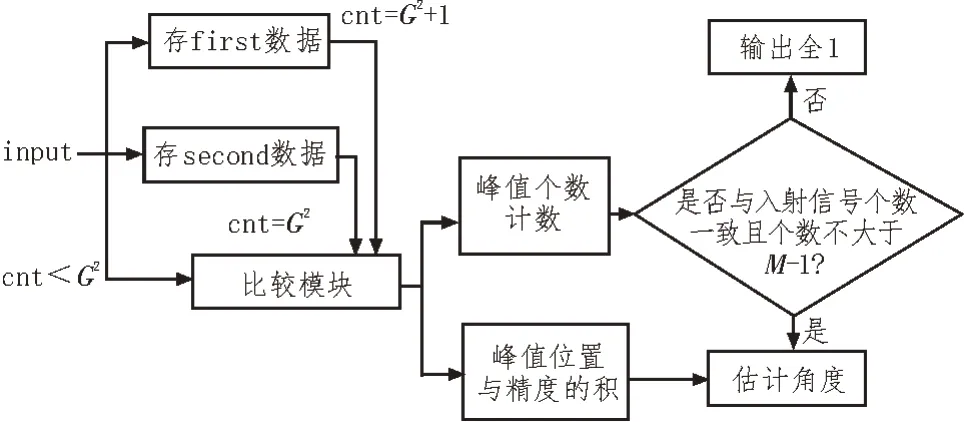
图2 谱峰搜索模块处理流程

首先，将谱峰值进行计数处理，并记录第一组和第二组谱峰数据；其次，当计数器小于G2时，将每相邻两个谱值进行比较，当计数器不满足上述条件时，将当前谱值与第一组和第二组谱值进行比较，再比较模块中谱值，同时与阈值EN进行比较，对满足条件的峰值个数进行计数并记录位置；最后，判别入射信号个数是否与空间谱计算模块中的入射信号个数估计一致且信号个数小于等于M-1，若不满足条件，输出全1；若满足条件，则根据谱峰位置和精度得到信号的来向估计。

3 仿真分析

首先，利用MATLAB 软件仿真MUSIC 算法对入射干扰信号来向和个数的估计性能；然后，验证MUSIC 算法在FPGA 上实现后的信号估计结果是否能实现干扰信号估计功能；最后，给出实际测试结果。仿真中，阵元数M=4，入射信号个数J=1，干信比为60 dB，入射信号俯仰角选择5°，方位角分别选择30°、90°、120°、180°，俯仰角精度Pp=5°，方位角精度Po=5°，为减小实际数据采集中的工作量，导向矢量计算中的数据均选择俯仰角为5°，因此暂不对俯仰角进行仿真分析。利用MATLAB 软件仿真的MUSIC 算法估计结果如图3 所示。

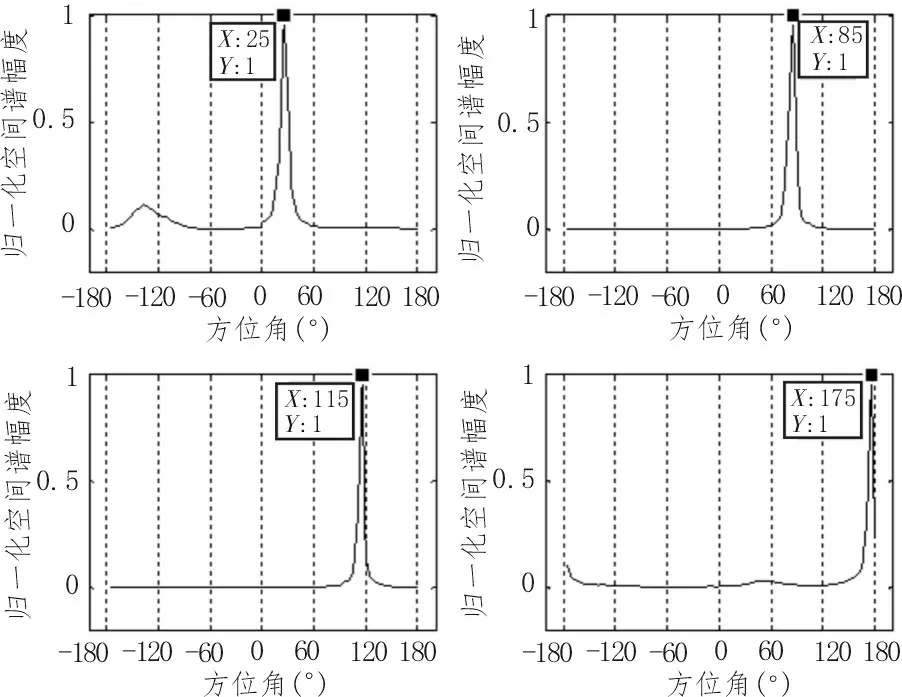
图3 MUSIC算法MATLAB仿真估计结果

从图3 可以看出，通过对MUSIC 算法的空间谱分析可知，估计的入射信号个数均为1，由于数据采集过程中存在误差，对应方位角为30°、90°、120°和180°的估计结果分别为25°、85°、115°、175°。通过测试可知，对干扰信号来向估计角度偏差小于等于10°时，对导航抗干扰的性能提升影响不大，因此，该估计结果引入的误差能够满足需求[9-12]。

为验证算法实现后的估计性能，图4 给出了空间谱计算模块实现后的仿真图，图5 给出了谱峰搜索模块实现后的仿真图。其中，阵元数M=4，入射信号个数J=1，干信比为50 dB，入射信号俯仰角选择5°，方位角为150°，俯仰角精度Pp=5°，方位角精度Po=5°。图4 中，dimen_act 表示阵元数设置；eig_data表示排序后的特征值；eig_vec 表示对应的特征向量；jump_num_cnt 表示估计的入射信号个数，从图中可知入射信号个数为1，估计准确；spec2peak_data 表示求得了空间谱值。图5 中，给出了入射信号角度估计结果，方位角估计结果为145°，算法在FPGA 上实现后能够实现角度估计功能。

图4 空间谱计算模块实现后仿真图

图5 谱峰搜索模块实现后仿真图

为验证MUSIC 算法在FPGA 上实现后的正确性和有效性，表1 给出了实际测试中的数据记录结果。测试中，分别设置干信比为50 dB 和100 dB。从表1 可以得出，实际测试中估计的干扰信号入射角度误差最大为5°，能够满足导航抗干扰算法中对预估角度的需求[13-16]。

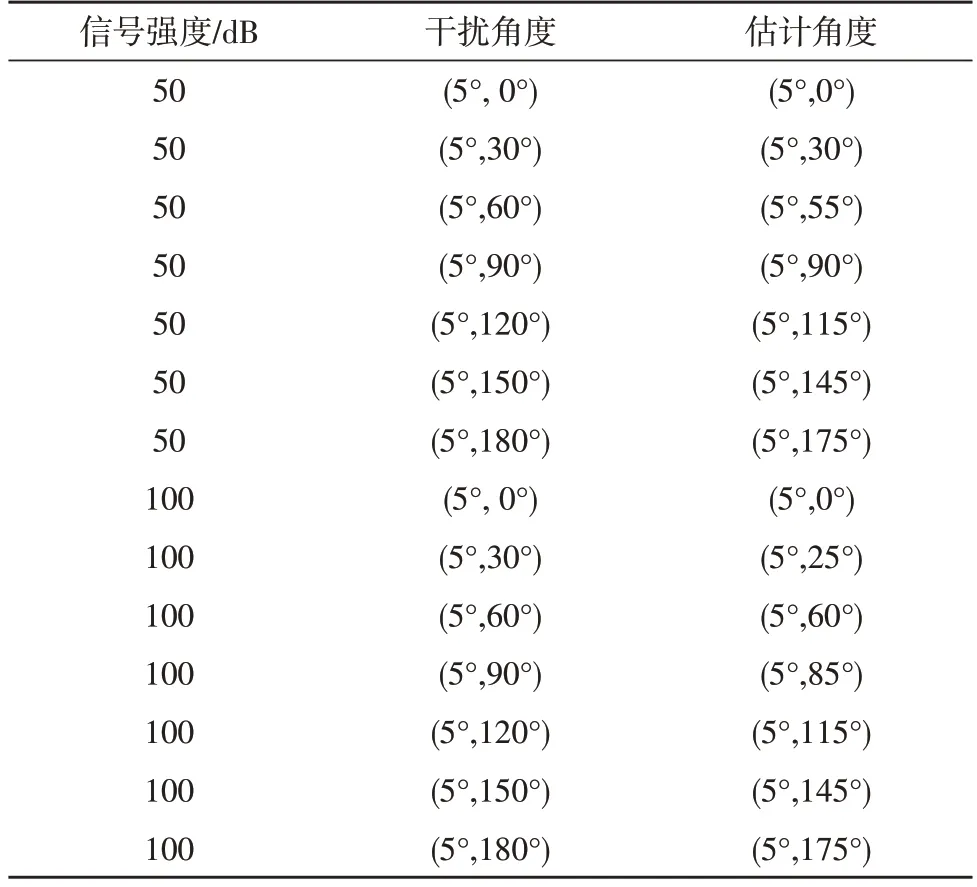
表1 实测数据记录结果

4 结论

信号来向估计对阵列信号处理中的抗干扰性能提升、敌方目标的精准打击与探测等多个方向都有重要的作用。在FPGA 上实现了二维MUSIC 算法，将信号来向估计技术从算法层面推广到应用层面。首先介绍了二维MUSIC 算法的算法模型和理论基础；其次给出了算法的实现步骤，根据实现步骤进行了算法的模块化划分；最后重点分析了特征值分解模块、空间谱计算模块和谱峰搜索模块的实现流程。仿真分析结果表明，所实现的二维MUSIC 算法能够准确估计入射干扰信号的个数，且对角度的估计在误差范围内。