城市轨道交通电力牵引动力负荷精准估计研究

路超，江海涛，孟昭明

（中车大连电力牵引研发中心有限公司，辽宁大连 116052）

当前，我国城市经济迅速发展，带动人口迅速增长，私家车数量逐年增加，同时，轨道交通的拥挤问题也随之产生[1]。为有效缓解车辆的拥堵问题，需要改善车辆的电力牵引问题，避免发生交通事故[2]。电力牵引供电系统是负责城市轨道安全运行的关键[3]。目前，使用的基于最小二乘多项式的电力牵引动力负荷精准估计方法，按照最小二乘多项式将谐波分量进行分类处理，由此得到训练集和测试集，用于负荷预测[4]；使用的基于贝塔函数的电力牵引动力负荷精准估计方法，结合馈线电流概率密度函数，判定城市轨道交通电力牵引动力负荷估计结果是否精准[5]。使用上述这两种方法仅从数据样本角度出发，一旦受到外界因素干扰，就会导致估计结果与实际测试结果存在一定差距。基于此，提出了城市轨道交通电力牵引动力负荷精准估计研究方法。

1 牵引系统结构

城市轨道交通电力牵引系统结构简图如图1所示。

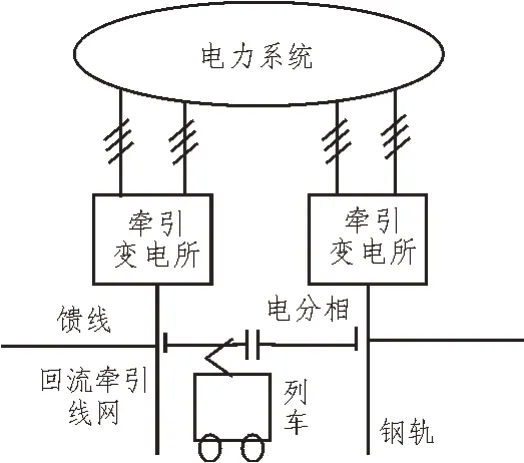
图1 电力牵引系统结构简图

从图1中可以看出，牵引车负责向系统提供电力，通过牵引网实现三相电压转换，从而牵引车辆行驶[6]。

2 电力牵引力动力负荷精准估计流程

电力牵引力动力负荷精准估计流程如图2所示。

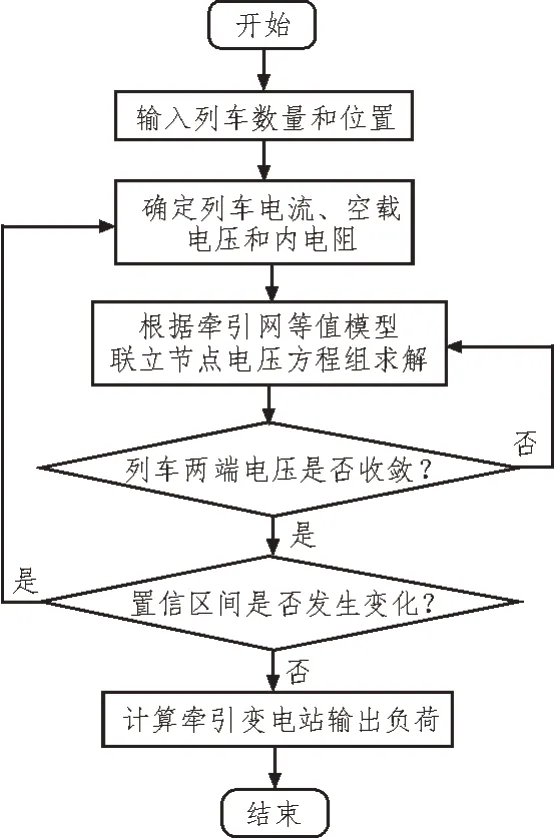
图2 电力牵引力动力负荷精准估计流程

2.1 列车合力计算

运用牵引力力学模型[7]，确定某一时段列车的数量、位置及负荷大小，在整流装置投入使用一段时间后，设置列车接触网初始电压[8]。

在城市轨道交通列车行驶过程中，作用在列车上的总合力为F，计算公式为：

式（1）中，F1表示牵引力，F2表示列车行驶阻力，F3表示列车制动力[9]。

列车总阻力包括基本阻力和附加阻力两种，其中，基本阻力包括列车自身阻力和空气阻力，这与列车行驶速度有关[10]；附加阻力指的是路面凹凸不平带来的阻力，在计算时，这些实际的附加阻力通常都转化为坡道阻力[11]。

2.2 列车运行阶段及工况分析

列车在加速、减速或匀速时，其运动可由合力来决定[12]。斜坡有一定阻力时，复合速度被称为平衡速度，不管斜坡的高度如何，列车在牵引或空转时，其速度往往保持平衡[13]。列车运行示意图如图3 所示。

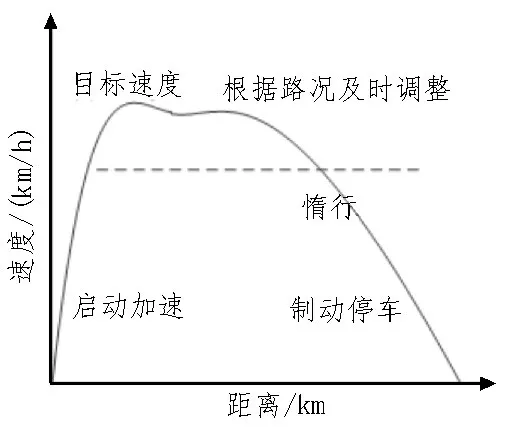
图3 列车运行过程示意图

由图3 可知，列车运行时长期受到行驶阻力的影响，牵引力和制动力随着行驶时间变化而发生改变[14]。因此，将列车运行过程中受到的力分为以下几种：

1）当列车行驶过程中，列车处于牵引工况时，列车受到的力的计算公式为：

2）当列车行驶过程中，列车处于惰行工况时，列车受到的力的计算公式为：

3）当列车行驶过程中，列车处于制动工况时，列车受到的力的计算公式为：

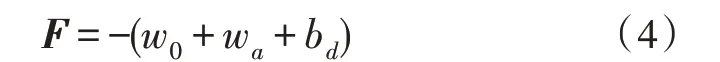
上述公式中，f表示列车单位牵引力[15]；w0表示单位阻力；wa表示坡道阻力；bd表示单位制动力。

2.3 牵引网模型构建

因为牵引电流并不是全部从运行轨道流回牵引变电所，而是由地面流回轨道和牵引变电所，因此，地漏电阻对等效电阻计算有很大影响[16]。基于均匀传输线原理，每条线路采用精确的等效二次电路，对轨道上、下两个方向进行严格地模拟。因上、下行走轨道间平均直线距离短，且测量数据不容易获取，故上、下行走轨道也可合并成一条直线用于一般工程计算，如图4 所示。

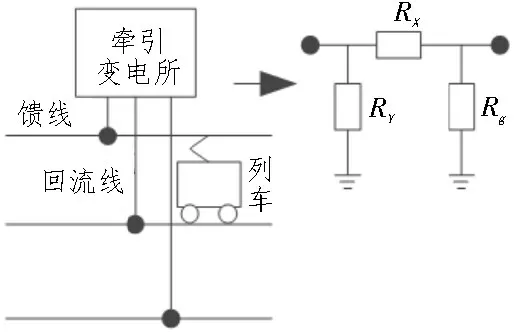
图4 牵引网模型

由图4 可知，轨道对地过渡等效电阻可通过轨道和大地之间产生的杂散电流和轨道电势得到，如式（5）所示：

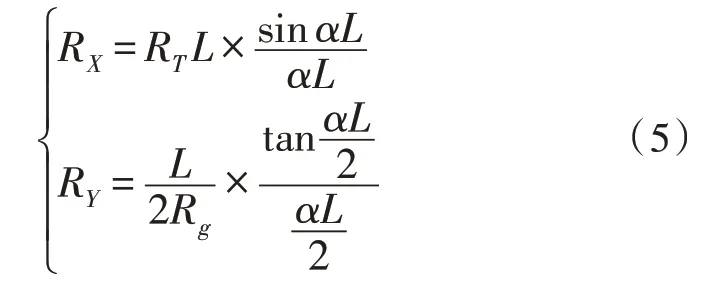
式（5）中，RX表示主线上的电路电阻；RY表示支路上的电路电阻；RT表示轨道单位电阻；Rg表示轨道的泄露电阻；α表示列车运行参数；L表示轨道长度。

2.4 动力负荷判断

通过构造节点导纳矩阵，建立节点电压方程，然后对各节点注入电压进行计算，以此判定列车两端电压是否达到设定的收敛精度，设注入节点电压为，判断依据为：

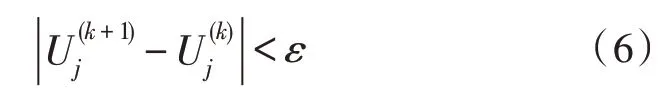
式（6）中，ε是收敛精度，若收敛则停止计算，若不收敛则调整注入节点电压，直至收敛为止。通过判断和计算整流机组接收电流的工作区间，使电压、电流在符合工作条件的电力牵引动力下达到最优解。

因为受测变电站的负荷功率不同于新线路，不能直接用已有线路建立的模型来预测未知牵引变电站的负荷功率，而是要根据变电站的平均等效负荷功率来预测，将样机的功率范围扩展到未知变电站。输入新建线路牵引变电所的负荷功率Pt如下：

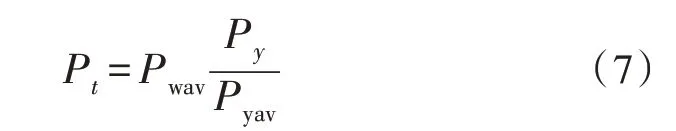
式（7）中，Pt、Py分别表示未知和已知的牵引负荷功率；Pwav、Pyav分别表示未知和已知的牵引负荷平均功率。

以牵引动力负荷Pt为输入值，给定置信度E在区间[0，1]之间，电流谐波概率分布满足如下公式：

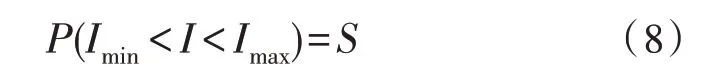
由式（8）可知，在[Imin，Imax]范围内，选择合适牵引动力负荷Pt对应的谐波电流值为估计结果，由此完成动力负荷精准估计。

3 实 验

使用MATLAB 软件作为验证城市轨道交通电力牵引动力负荷精准估计研究合理性的实验工具，方便实验分析。

3.1 实验项目分析

以某市的地铁1号线为例，该地铁通过DC1 500 V方式供电，是一种集中供电手段。通过估计1 号线高峰时期的单向客流量最大值约为3.55 万人。使用6 辆固定编组的列车，统计每列列车上的载客数量为1 550 人。地铁1 号线全长为35.50 km，全线共设置30 座。地铁1 号线近、中、远期情况，如表1 所示。

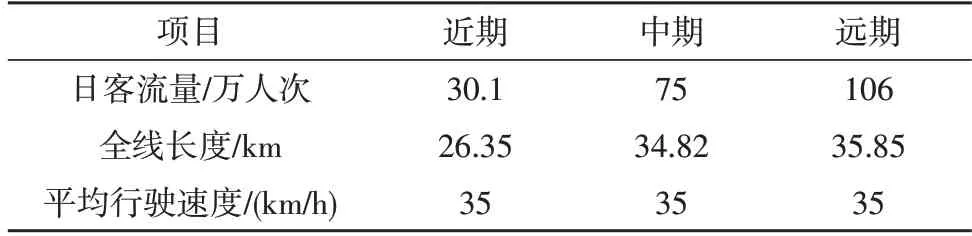
表1 地铁1号线近、中、远期情况

结合上述统计数据，分析电力牵引动力负荷各个特征电流向量。

3.2 实验结果与分析

分别使用基于最小二乘多项式、贝塔函数和所研究估计方法的电力牵引动力负荷精准估计方法对比分析日负荷预测精准度，对比结果如图5 所示。

由图5（a）可知，在时刻为8:00 时，牵引日负荷达到首个高峰值为4×104kW。在时刻为11:30 时，牵引日负荷达到第二个高峰值为3.8×104kW。在时刻为14:30时，牵引日负荷达到第三个高峰值为3×104kW。在时刻为18:30 时，牵引日负荷达到第四个高峰值为3.7×104kW。使用所研究的方法与日负荷预测轨迹一致，误差为0，使用基于最小二乘多项式、贝塔函数和所研究估计方法与实际日负荷预测结果不一致，最大误差均为2.2×104kW。

由图5（b）可知，在时刻为8:00 时，牵引日负荷达到首个高峰值为11.5×104kW。在时刻为12:00时，牵引日负荷达到第二个高峰值为9×104kW。在时刻为17:00 时，牵引日负荷达到第三个高峰值为9.5×104kW。使用所研究的方法与日负荷预测轨迹一致，误差为0，使用基于最小二乘多项式、贝塔函数和所研究估计方法与实际日负荷预测结果不一致，最大误差分别为1×104kW 和1.2×104kW。

由图5（c）可知，在时刻为8:00 时，牵引日负荷达到首个高峰值为11.5×104kW。在时刻为12:00时，牵引日负荷达到第二个高峰值为9×104kW。在时刻为18:30时，牵引日负荷达到第三个高峰值为11×104kW。使用所研究的方法与日负荷预测轨迹基本一致，但存在一定误差，最大相差0.3×104kW。使用基于最小二乘多项式、贝塔函数和所研究估计方法与实际日负荷预测结果不一致，最大误差分别为2×104kW和2.5×104kW。

4 结束语

文中提出的城市轨道交通电力牵引动力负荷精准估计方法的研究，为新线路的设计、供电和电网评估发挥了重要的作用。但仍存在不足之处，需要进一步改进和拓展。在今后的实际工程中，对于不同的牵引负荷边界条件的选择，可根据不同城市线路所处的地理位置、列车类型、车次、速度等条件，进一步改进边界条件的选择，区分样本空间中不同的边界条件，从而更准确地预测新的负荷模型曲线。