基于复杂缝网模拟的页岩气水平井立体开发效果评价新方法——以四川盆地南部地区龙马溪组页岩气为例

王军磊 贾爱林 位云生 王建君 黄小青 李 林 于 伟

1.中国石油勘探开发研究院 2.中国石油浙江油田公司 3.得克萨斯大学奥斯汀分校

0 引言

页岩气是一种通过大规模体积改造获得工业产能的特殊气藏类型。合理的井位部署和水力压裂方案能够有效提高页岩气的开发效果[1]，国内外页岩气开发者通常采用理论模拟和现场试验等手段论证合理井距和井网模式。“小井距、密井网”已成为北美各页岩气田主流的开发方式，但同层内部署井距过小可能导致严重的压窜风险和强烈的井间干扰[2]，而部署立体井网却能够有效提高平面间和层段间的地质储量动用程度，同时缓解压裂、生产过程中的井间应力阴影及压力干扰。因此，立体井网研究近年来受到了越来越多的关注[3-5]。

页岩气井网井距模式研究的核心问题是平衡好井网井距与体积压裂的匹配关系。美国二叠系盆地井网加密过程中，大量实践表明母井生产将引起压力波及范围内地应力的方位角及数值大小发生不同程度变化，直接影响加密井的部署[6-8]。四维应力场模拟广泛用于研究Eagle Ford页岩中母井泄压对子井压裂效果的影响，根据地应力的时空演化结果确定子井加密时机及加密井距[9]。地质力学模型模拟也成功应用于Marcellus页岩中的井间应力干扰效应分析，通过建立井距与单井压裂规模之间的关系图版，根据邻井间裂缝重叠率确定最优井距[10]。在设计立体井网时，井间干扰识别模型能够模拟三维空间中的压力（应力）干扰，通过量化井间干扰程度，进而确定合理的平面及纵向井距[11]。根据二叠系下部母井生产后的压力场，更新上部地层非均质应力场，利用压裂模型模拟上部加密井的裂缝延伸，以此论证不同立体井网模式下的气井生产动态[12]。

相较于美国采用的“滚动开发”模式，中国川南页岩气通常采用一次性井网整体部署方式开采，为了确保一次性部署的可靠性，不同学者基于地质—工程—经济一体化的流程，采用不同模拟手段来优化页岩气的水平井距[13-16]。值得注意的是，美国二叠系盆地多层立体井网纵向错开距离较大，上、下部水平井靶体间距普遍超过25 m，对缝高模拟精度要求不高[14]，而川南页岩气目前有效动用层位更薄，上、下部水平井纵向交错空间有限[17]。研究表明川南地区的人工裂缝横截面呈现“星”形特征[18-19]，部署“W”形上、下两层交错井网具有可行性。在昭通地区开展的页岩气小井距错层开发先导性试验也取得了较好的开发效果，但模拟研究所使用的非结构化网格难以表征地层三维空间流动和天然裂缝影响，无法准确模拟纵向上的井间干扰[20-21]。

综上所述，如何合理表征三维人工裂缝形态及延伸范围、模拟压后复杂缝网产能特征是论证立体井网开发效果的关键。笔者利用压裂模型充分考虑了天然裂缝对人工裂缝延伸的影响，将激活的天然裂缝与人工裂缝共同构成复杂裂缝网络，利用嵌入式离散裂缝模型模拟三维缝网生产动态，从纵向水平井靶体优选、平面井距优化等两个维度来评价立体交错井网开发效果；结合人工智能历史拟合，以动态数据为约束获得有效缝网参数，建立立体井距与裂缝的配置关系，为页岩气藏（井）产能的高效评价和开发技术政策优化提供有力技术支撑。

1 模拟方法

笔者使用压裂模型模拟岩石变形、缝内流体流动和水力裂缝延伸等过程，该模型基于拟三维原理，缝长延伸采用位移不连续法[22]，缝高延伸采用非平衡裂缝高度模型计算[23]。人工裂缝与激活的天然裂缝构成压后复杂缝网，使用嵌入式离散裂缝模型模拟复杂缝网流动过程[24]。

1.1 裂缝长度模拟

使用位移不连续法对裂缝进行边界元离散。弹性区域内各个点处的应力等于区域内所有点处发生的位移不连续影响线性叠加（即应力阴影效应），则第i个边界元上的正应力、切应力满足下式：

式中σn表示正应力，MPa；σs表示切应力，MPa；Nf表示单元数量，无量纲；Ds表示剪切位移不连续量，m；Dn表示法向位移不连续量，m；Cns、Cnn、Css、Csn表示弹性影响系数矩阵；Gij表示考虑有限缝高的Olson三维修正因子[25]，其计算如下：

式中hf表示裂缝高度，m；dij表示第i个与第j个微元距离，m；α、β表示经验常数，α=1，β=2.3。

由于裂缝宽度（wf）远远小于裂缝长度，可忽略压裂液沿裂缝宽度方向的流动，仅考虑压裂液沿裂缝扩展方向上的一维流动。随着压裂液注入，缝内流体压力、裂缝宽度和裂缝尖端应力强度因子不断增加，当裂缝尖端处岩石变形达到临界点时，裂缝开启并且沿特定方向继续延伸。根据线性弹性断裂力学，当开启型裂缝尖端应力强度因子（KI）等于岩石断裂韧性（KIC）时，裂缝即发生开启。裂缝延伸方向（θ）遵循最大圆周应力准则，满足下式：

式中KII表示滑移型应力强度因子。

KI和KII分别是关于裂缝尖端处的剪切、法向方向位移不连续量与杨氏模量、泊松比的函数，可以通过Olson公式获得[25]。将岩石变形和缝内流体流动的控制方程在相同的边界元网格上离散，在每一个时间步中，增加新的计算单元，使用牛顿迭代法求解非线性方程组，以确定新增单元的长度和延伸方向。裂缝的延伸过程即为新增单元的过程。

当存在天然裂缝时，水力裂缝与天然裂缝将产生相互作用。根据水力裂缝与天然裂缝相交处的最大拉应力与天然裂缝面的正应力、剪应力以及岩石抗张强度之间的关系，可以判别裂缝扩展路径，共3种典型模式[26]：①水力裂缝未穿过天然裂缝，沿天然裂缝转向延伸；②水力裂缝穿过天然裂缝，天然裂缝部分开启；③水力裂缝穿过天然裂缝，且沿天然裂缝转向延伸。水力裂缝能否穿过天然裂缝可根据非正交判别图版，基于正交判别准则，当考虑界面处内聚力后判别准则可修正为[27]：

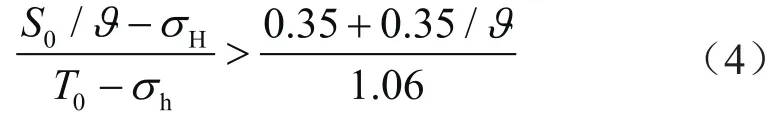
式中S0表示界面内聚力，MPa；表示摩擦系数，定义为两表面间摩擦力与作用在表面上的垂直应力的比值，对于多数岩石该值介于0.1～0.9；T0表示岩石抗拉强度，MPa；σH表示最大水平主应力，MPa；σh表示最小水平主应力，MPa。

当水力裂缝未与天然裂缝相交时，天然裂缝能否开启取决于人工裂缝内流体压力、最大（最小）水平主应力及天然裂缝夹角，其关系为[28]：

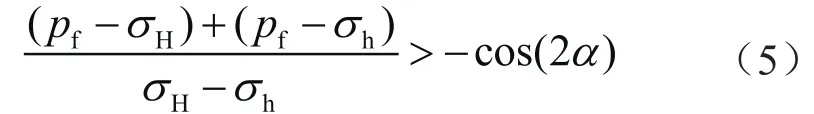
式中pf表示裂缝内的流体压力，MPa；α表示天然裂缝方位角与最大水平主应力之间的夹角，(°)。

根据上述裂缝扩展原理，使用复杂缝网压裂模拟器（UFM）[23]，模拟二维条件下考虑天然裂缝的人工裂缝延伸规律。其中天然裂缝设定为两组随机均匀正交分布的裂缝系统，其他模型参数包括地质力学性质参数、地应力参数和压裂泵入参数等（表1）。

表1 页岩储层基础地质及压裂施工参数表

研究表明除岩石力学参数外，水平主应力差是影响水力裂缝在天然裂缝内延伸的最主要因素，图1模拟了天然裂缝与人工裂缝45°夹角下主应力差对人工裂缝延伸的影响（图中粉红色线条表示水平井筒）。当地应力差较小时（图1-a），初期主裂缝内流体压力较高，满足裂缝扩展路径模式③，随着缝内压力迅速降低，满足裂缝扩展路径模式②，人工裂缝更易沿天然裂缝延展；每段中各簇裂缝形态差异性较大，缝网宽度和增产改造面积较大，带长较短，形成更为复杂的裂缝网络。当地应力差较大时（图1-b），满足裂缝扩展路径模式②，人工裂缝不易弯曲，易形成直缝，并且每段中各簇裂缝长、短差异性较小，天然裂缝被激活形成分支裂缝，与主裂缝组成复杂缝网；激活的天然裂缝在较小范围内达到最大主应力方向，缝内压力递减较快，带长方向延伸较远，裂缝向外扩展较难，形成的缝网带宽较小。

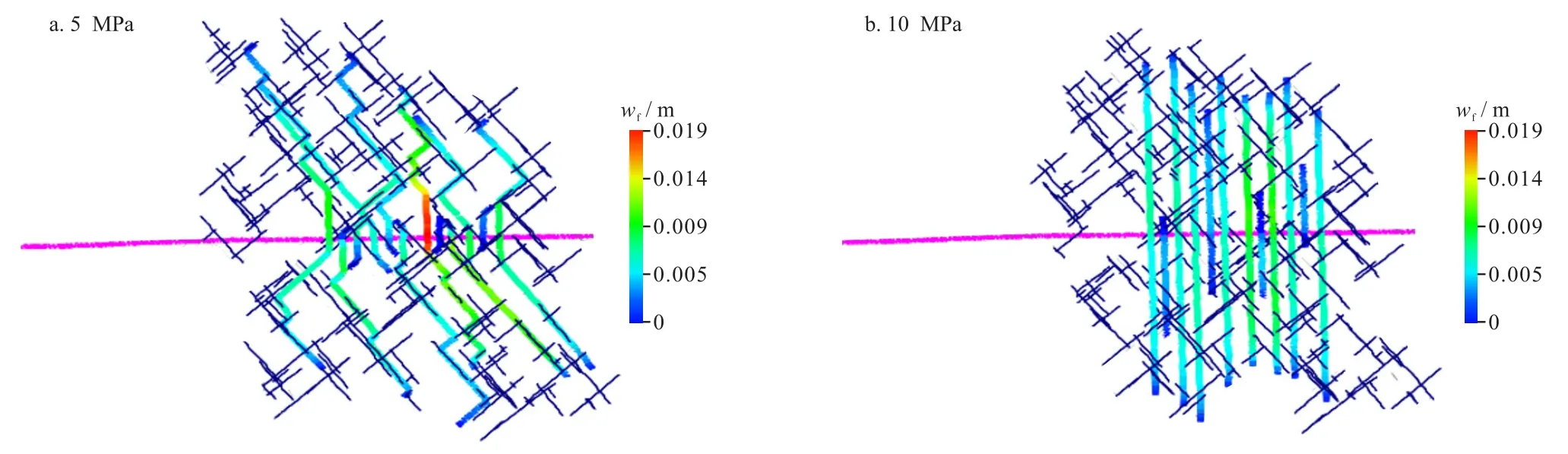
图1 不同地应力差缝网模拟结果图

1.2 裂缝高度模拟

在多地层模型中，裂缝高度取决于地应力、界面力学属性、断裂韧度、压裂液滤失、岩石力学属性（包括杨氏模量、剪切模量、泊松比、抗拉强度）等因素。其中，地应力是控制裂缝高度最重要的因素，其值越大，裂缝高度越小；界面力学性质越弱，裂缝高度越易保持不变；高断裂韧度能够控制裂缝高度的增加，但断裂韧度只在裂缝高度较小时发挥作用；较高的杨氏模量能够降低裂缝宽度、增加压降，进而形成较小的裂缝高度；压裂液滤失率较高将引起缝内流体压力降低，阻碍裂缝高度增加。

当裂缝高度模型不考虑垂直方向上的流体流动和压力梯度影响时，该模型本质上是多地层裂缝平衡高度力学模型。裂缝高度与裂缝上尖端强度因子（KI-）、下尖端强度因子（KI+）之间的关系满足下式[23]：

式中hf表示裂缝高度，m；pnet表示净压力，MPa；σi表示第i层地应力，MPa；hi表示从裂缝尖端到第i层地层顶部的高度，m；n表示裂缝高度穿透的地层数量。其中，净压力（pnet）满足下式：

式中σn表示地层顶部地应力，MPa；hcp表示参考深度，一般选射孔段深度，m；pcp表示参考深度处裂缝内的流体压力，MPa；ρf表示流体黏度，mPa·s。

当考虑裂缝高度方向上的压力梯度时，该模型改进非平衡高度模型。需要强调的是这种模型仅适用于含有单个裂缝前缘且起裂点位于最低应力层的情况，更为复杂的裂缝高度模拟可参考本文参考文献[29]。

1.3 缝网生产动态模拟

在天然裂缝基础上，通过压裂模拟在裂缝长度和裂缝高度方向上获得了三维人工裂缝形态，基于正交网格，采用自主研发的嵌入式离散裂缝模型（EDFM）处理复杂的裂缝网络[24]。EDFM原理在于：①根据裂缝与正交网格的分布特征，裂缝被网格分解为一系列的裂缝元并产生相应的虚拟网格作为裂缝计算域，实际物理域被分解为两套网格系统；②虚拟网格通过非邻近连接对（NNC）与实际网格和其他虚拟网格耦合，裂缝通过有效井筒连接系数（WIf）与井筒耦合。EDFM技术核心在于NNC的计算，主要用于处理物理模型上相邻但在计算域上不相邻网格之间的流量交换。

非邻近连接对之间通过传导率连接，网格之间的流体流速（q）满足下式：

式中λ1表示流体流度，m2/(Pa·s)；TNNC表示传导率，m2；Δp表示压力差，MPa。

非邻近网格连接对的传导率（TNNC）计算通式为：

式中kNNC表示连接渗透率，mD，当裂缝与基质间连接时，kNNC表示基质渗透率；当裂缝与裂缝连接时，kNNC表示裂缝平均渗透率；ANNC表示连接对之间的接触面积，m2；dNNC表示连接对之间的距离，m，当裂缝与基质间连接时，dNNC表示基质块到裂缝面的平均距离；当裂缝与裂缝连接时，dNNC表示裂缝元之间的法向距离。

在人工裂缝形成过程中，裂缝延伸的同时裂缝宽度形成且保持较高的渗透率。在生产过程中，随着裂缝有效应力增加，支撑剂发生破碎、溶蚀、嵌入等作用，裂缝渗透率递减，但残余颗粒具有一定渗流能力，最终裂缝保持恒定的最小裂缝渗透率（kf,min），其满足下式[30]：

式中γf表示裂缝应力敏感参数，MPa-1，其值介于10-8～10-6MPa-1；kf,i表示原始地层压力下裂缝渗透率，mD。此外，模型还考虑了吸附气解吸、人工裂缝内气水两相渗流等机理，相应内容可参考文献[31]。

以图1所形成的复杂缝网为对象，利用EDFM技术模拟其产能动态。气藏采用三维单孔单渗数值模型，地层尺寸为1 700 m×800 m×20 m，地层渗透率为8.85×10-5mD，孔隙度为6.28%，含水饱和度为35%，原始地层压力为42.5 MPa，水平井长度为1 500 m，井底采用2.5 MPa恒压生产。模型包括3种尺度空间（基质、天然裂缝和人工裂缝），基质系统采用规则正交网格，裂缝系统（天然裂缝+人工裂缝）使用EDFM产生的虚拟网格描述，通过非邻近网格连接对的传导率计算考虑各类孔隙间的流体传递特征。图2展示了高、低应力差条件下的缝网累计产气量（Gp）。

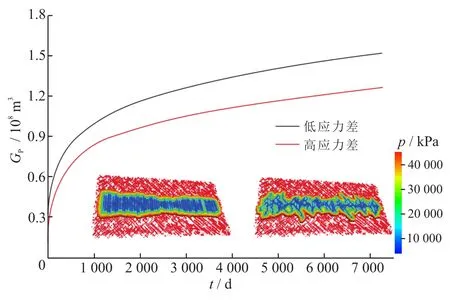
图2 高、低应力差条件下形成缝网的产能模拟结果对比图

对比高、低应力差条件下的生产动态曲线及泄流体积可知，在低应力差条件下，缝网与地层具有更大的接触面积，缝网交错且导流能力分布较为均匀，导致缝网覆盖区域内压力下降程度相对较小，压力场更为均匀，累计产气量始终较高。在高应力差条件下，缝网复杂程度较低，主裂缝沿最大水平主应力方向近似平行分布，裂缝间压降较大，同时裂缝内高导流能力主要集中在近井筒区域，靠近主裂缝尖端区域导流能力较低，裂缝整体导流能力不均匀，导致裂缝产能较低。至此，形成集合人工裂缝延伸和产能模拟的模拟方法，用以评价立体井网开发效果。

2 基于三维裂缝模型的立体井网模型

页岩气井产能取决于地质因素和工程因素两大类，包括储层品质（如TOC、优质储层厚度、压力系数、天然裂缝、脆性指数等）、钻井品质（如水平井靶体及钻遇率、水平井钻井设计、井筒完整性等）、完井品质（如压裂参数设计）和开发品质（如压后焖井、返排和生产制度等）[32]。其中，储层品质是先天条件因素，决定了页岩气储层的“质量”“数量”和“能量”；而钻井品质、完井品质和开发品质是后天努力因素，共同决定了页岩气储量的“动用量”。“质量+数量+能量”是开发对象的条件，“动用量”是开发设计的目标。在后天努力因素的领域内，页岩气开发过程中面临4大优化难题，即部署阶段的井距优化、钻井阶段的水平井靶体优选、完井阶段的压裂方案优化和投产阶段的生产制度优化。以上问题相互关联且具有继承性。从开发设计角度看，立体井网部署是解决以上难题的基础[33]，即通过优选水平井靶体和井距，提高层间、井间储量动用率，通过优选压裂方案和生产制度方案提高单井可采储量。

立体井网部署首先优选水平井靶体层位，进而分别在不同层位内优化水平井距、设计单井压裂方案和生产制度，最终形成整体开发效果最佳的立体开发井网。

2.1 水平井靶体优选

基于川南龙马溪组页岩气开发评价井的测井解释成果，建立三维地质模型和地质力学模型。模型尺寸为2 560 m×800 m×30.85 m，平面网格尺寸为10 m×10 m，纵向网格介于0.60～3.37 m，水平井方位为NE10.00°，最小主应力方向为NE11.91°，水平井方位与最小主应力方向基本保持一致。平面属性假定为二维均质，纵向按地质特征共分为5个小层（0～4号），根据各小层属性差异共细分为30个网格，各小层主要地质参数如表2所示。

表2 三维地质模型纵向各小层主要地质参数表

模型中的工程品质参数包括最大水平主应力（σH）、最小水平主应力（σh）、泊松比（ν）、杨氏模量（E）等，储层品质因素包括孔隙度（φ）、渗透率（km）、地层压力（p）、含气饱和度（sg）等，工程品质和储层品质参数纵向分布如图3所示。

图3 工程品质和储层品质参数纵向分布图

以单级压裂段为例，采用表1中泵注程序利用压裂模型模拟水平井靶体位于不同层位时形成的人工裂缝形态，压裂模拟如图4所示。设定裂缝宽度大于阈值（0.05 mm）的区域为支撑裂缝分布区域（图中红色区域），相应统计结果如表3所示。从表3可知，裂缝体积从大到小依次为3号、4号、1号、2号、0号，结合压裂模拟三维结果（图4），纵向上水平井靶体位于0～4号任一层段时水力裂缝均能上、下穿透整个目的层位，考虑到裂缝宽度在裂缝高度方向上与起裂点的对应关系，支撑裂缝区域集中在水力裂缝下部。

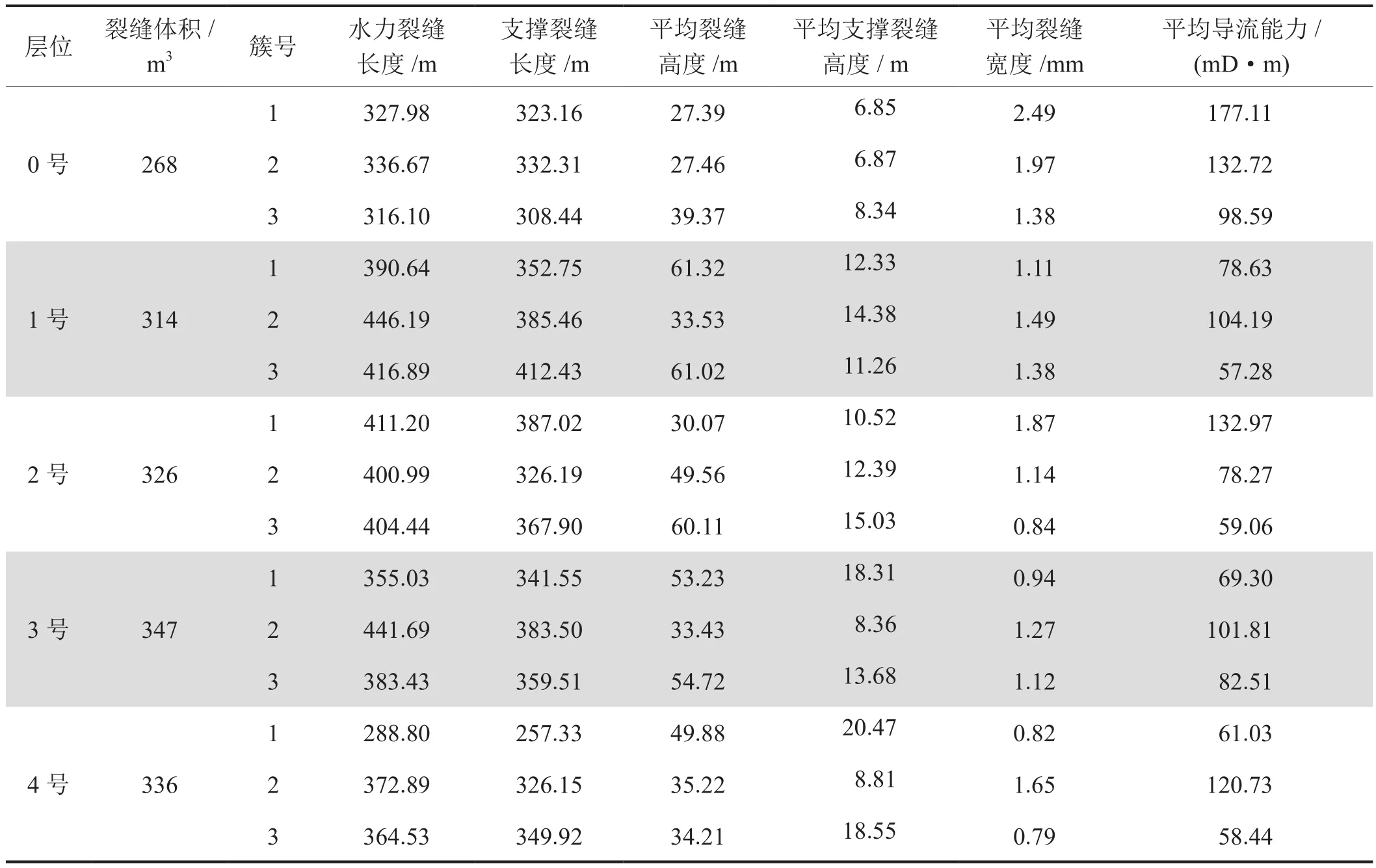
表3 不同靶体位置下人工裂缝扩展模拟结果对比表

图4 靶体位于不同层位时三维裂缝延伸模拟图

根据三维裂缝形态模拟裂缝产能特征，由各小层储层品质与裂缝导流能力共同决定。高导流能力意味着流入程度高于流出程度，流体在裂缝内压降幅度小，有利于裂缝产能发挥；低导流能力意味着流出程度更高，流体在裂缝内流动发生显著的压降，不利于裂缝产能发挥。

设定井底恒定压力2.5 MPa开井生产，模拟靶体不同层位下的单段裂缝生产动态（图5）。笔者定义生产时间为20年后的最终可采储量（EUR）为压后产能，由高到低依次为1号、2号、3号、4号、0号，其特征为：①靶体位于1号小层时，裂缝高度主要覆盖1～3号小层，对应地层的单储系数较高，孔渗性较好，同时裂缝与地层接触面积较大，缝内导流能力较高，充分发挥了相应层段的储量基础和裂缝导流能力，因此，裂缝EUR最高、累计产量上升幅度最快（前3年累计产量占比EUR约为72%）；②靶体位于0号小层时，由于支撑裂缝高度过小，有效动用层段仅为0～1号小层，虽然裂缝导流能力较高，但受制于有限的储量基础，单段EUR最低；③靶体位于4号小层时，有效动用层段为3号小层、4号小层及2号小层上部，裂缝体积较大，裂缝导流能力低，表现为早期累计产量增长幅度较小，前3年累计产量占比EUR约为38%，动用层位厚度较大，但对应层段的孔渗性较差，导致裂缝EUR较低；④靶体位于2号小层时，与靶体位于1号小层相比，形成的裂缝体积较大，但裂缝高度更大、裂缝宽度更小，导致裂缝导流能力略有降低，对应的EUR值比1号小层靶体的EUR值低；⑤靶体位于3号小层时，改造效果与动用层位与靶体位于4号小层类似，呈现相似的动态特征。

图5 靶体位于不同层位时三维裂缝产能模拟结果图

2.2 立体井网模式

根据靶体位于不同层位所形成的支撑裂缝高度，结合对应的裂缝产能，在确保足够纵向空间以避免裂缝高度压窜的前提下，立体井网靶体分别部署在1号小层和4号小层，同时平面上邻井采用交错布缝，最大限度避免压窜，部署模式如图6所示。通过部署两层水平井，纵向储量控制程度大幅度增加。

图6 立体井网部署模式图

以3口井为例，中间井部署在4号小层，两侧井部署在1号小层。图7模拟了平面投影井距介于250～400 m的单井产能，井距小于等于300 m时，井间开始发生显著干扰。当井距为300 m时，靶体位于1号小层的水平井井间干扰强度较低，而靶体位于4号小层水平井在生产后期已发生较为显著的井间干扰，原因在于：①同一层位内水平井尚未产生干扰，同层内对应井距为600 m，如图7-a所示，靶体位于1号小层两口水平井独立生产，无显著压力连通；②上、下两套水平井通过3号小层内产生纵向上干扰，靶体位于4号小层的三维裂缝，导流能力低于靶体位于1号小层的裂缝，导致其在地层内的导流能力不足，井间干扰对其产能影响程度更大。当井距为200 m时，下部水平井（靶体位于1号小层）也开始发生显著的井间干扰，主要来自于同一层位内水平井之间的压力干扰，同时上层水平井产能下降幅度进一步增加。

图7 立体井网中水平井生产动态模拟图

为了突出立体部署相对于同层部署在井距设计中的优势，设计两种对比模式，即同层模式（靶体全部位于1号层位）和立体模式（靶体交错位于1号和4号层位）。横向地层距离800 m分别设置1～4口井（对应井距分别为800 m、400 m、266 m、200 m），考虑天然裂缝影响。

同层模式（图8）：当井距大于等于400 m时，井间几乎无干扰，单井全生命周期产能几乎不受干扰影响，区块采收率（EOR）随井距减小呈线性增加；当井距小于400 m时，井间存在显著干扰，单井产能受抑制，表现为区块采收率增加幅度逐渐降低；当井距继续降低时，井间裂缝出现压窜，井间干扰急剧增加，当裂缝完全连通时，继续减小井距对提高区块采收率无显著作用。从纵向动用程度上分析，靶体位于1号小层时，裂缝高度主要控制1～3号小层，根据裂缝截面形态，其对下部地层控制作用更为显著，而在上部地层中裂缝截面变小，加之纵向渗透率极低，上部层位储量难以动用。

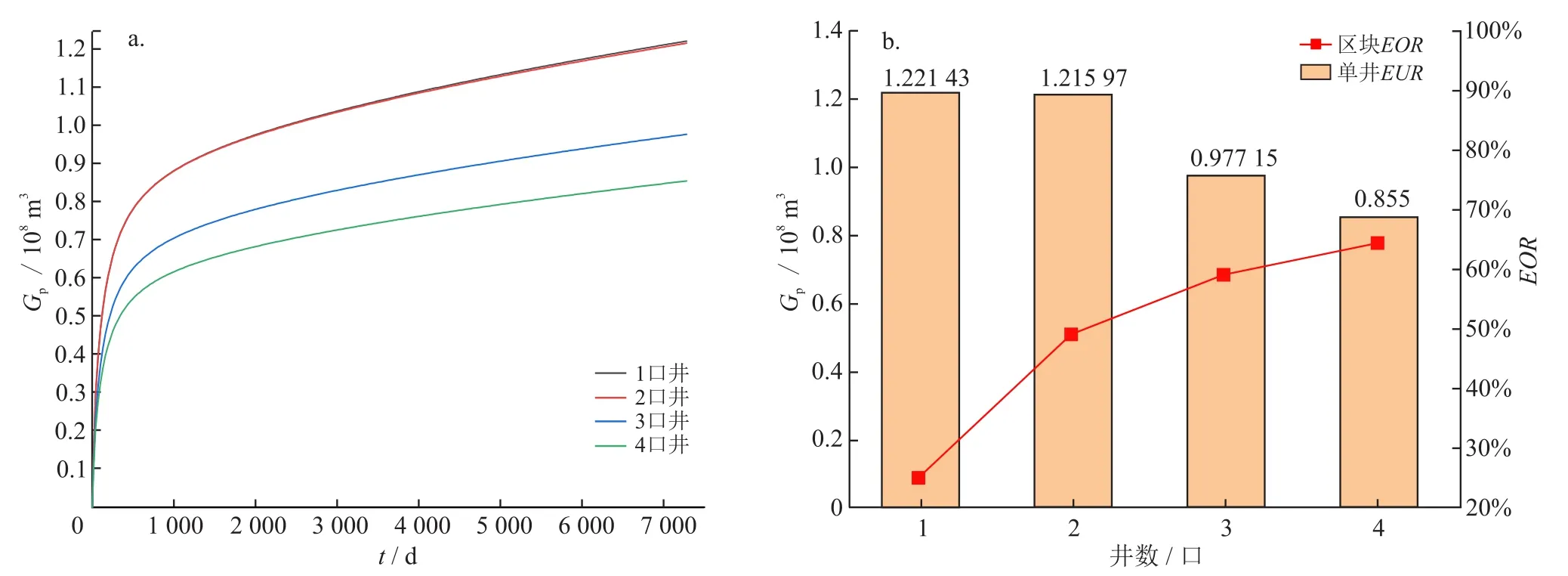
图8 同层模式下井距对单井EUR及EOR的影响图

立体模式（图9）：以3口井为例（井距为266 m），图9对比了同层模式与交错模式下的单井EUR和区块EUR。

图9 立体井网对单井EUR影响图

定义单井产能井间干扰率（或产能损耗率）为：

式中EURsingle表示单井独立生产时的单井EUR；EURmultiple表示多井生产时的单井EUR。

图9-a为同层模式下靶体分别位于1号和4号小层时的单井生产动态曲线，其中靶体位于1号小层时井间干扰率（19.9%）明显高于靶体位于4号小层的井间干扰率（9.9%），主要原因在于前者主力动用层段的地层孔渗性好于后者，良好的地层传导效率增加了井间干扰程度，这与压力波传播距离规律一致。图9-b中井网变换为交错部署，通过水平井靶体层位调整，上、下部水平井的井间干扰率均发生了明显下降（图9-b中下部井的井间干扰率9.9%降为5.2%，上部井的井间干扰率19.9%降为15.5%），强度较弱的纵向干扰一定程度上缓解了同层部署时的平面井间干扰。图9-c为不同部署模式下的区块EUR对比。相比其他两种模式，靶体均位于4号小层时，虽然井间干扰程度较低，但受制于上部单井EUR规模，区块EUR整体仍然较低；而交错部署模式，通过部署1口产能较低的上部井，有效缓解了井间干扰，区块EUR反而略高于靶体均位于1号小层的同层模式。

图10进一步对比了更小的井距条件下同层模式（靶体均位于1号小层）与立体模式的产能结果。井距减小意味着同一区块内可部署井数增加，区块EUR将逐渐提高，但增长幅度逐渐降低；立体交错模式通过提高纵向控制范围，合理规避同层间、纵向间干扰，将上、下部储层联合动用，随着井距减小，该模式相对于同层部署的趋势更为明显，区块EUR提升幅度在266 m井距下为1.37%，在200 m井距下提升到6.51%。

图10 不同模式下井距对区块EUR的影响图

3 实例分析

3.1 立体井网开发效果

选取昭通某页岩气立体开发平台进行实例分析，建立三维地质力学模型、三维地质模型和天然裂缝模型，根据泵注参数，借助压裂模拟模型模拟人工裂缝（图11）。该平台共设计3口井，其中井2位于中间，设计靶体在4号小层，其余2口井靶体在1号小层，平面投影井距介于275～305 m，主要的钻井及压裂参数如表4所示。实钻监测表明轨迹控制较好，纵向上靶体错开超过12 m，基本实现小井距立体开发，满足设计要求。

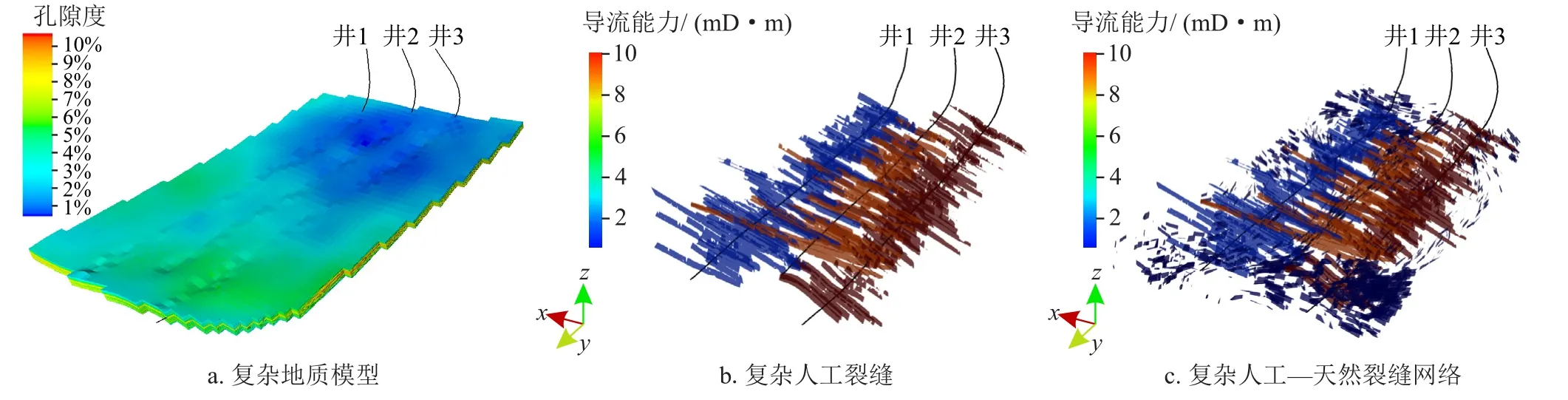
图11 三维地质模型及人工—天然裂缝模型图

表4 试验井组各井主要施工参数表

建立嵌入式离散裂缝模型对3口井同时生产进行模拟。基于蒙特卡洛—马尔科夫机器学习算法，利用神经网络训练获得代理模型，形成智能算法驱动自动历史拟合技术[34]，实现了高效、精确评估复杂裂缝系统的有效性（包括有效裂缝高度、裂缝长度、导流能力）。算例采用多井同步自动历史拟合，分别以井底压力数据作为各井的输入条件，共进行8步自动迭代，全局误差设定小于4.5%，从中优选出65套历史拟合解，拟合效果如图12所示（以井1为例）。

图12 历史拟合解与实测数据的对比图

以人工裂缝延伸模拟结果（裂缝长度、裂缝高度、导流能力）作为初始待拟合参数，历史拟合过程中假定裂缝参数等比例变化，校正后的人工裂缝参数统计结果如图13所示：井1平均支撑裂缝高度为17.18 m，平均支撑裂缝长度为267 m，平均导流能力为75 mD·m；井3平均支撑裂缝高度为22.77 m，平均支撑裂缝长度为198.87 m，平均导流能力为125 mD·m；靶体位于上部的井2平均支撑裂缝高度为30.13 m，平均支撑裂缝长度为298.78 m，平均导流能力为136 mD·m。

图13 校正后的人工裂缝参数统计图

对校正后的复杂裂缝网络进行产能模拟（图14）。图14-a为3口井同步生产时的累计产气量曲线，井1～井3的单井EUR分别为8 011×104m3、6 599×104m3、7 311×104m3。相对于井3，井1靶体位于下部层位，对应层位的产能潜力较大，虽然裂缝导流能力较低，但水平段较长，压裂级数较多，保证了缝网与地层的接触面积，有足够大的缝网接触面积，从而保证了水平井的产能。中间的井2位于上部地层，储量基础和地层孔渗性均较差，加之井2与邻井发生较大规模压窜，而邻井产能又较高，增加了井2受干扰的程度，导致其气井产能明显低于其他2口井，对应的单井产能井间干扰率也最高（图14-b），干扰率比邻井高8%左右。

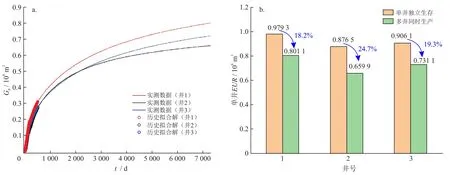
图14 立体井网产能模拟结果图

整体来看，该井组采收率达到27.5%，较周围采用400 m井距的开发井组采收率提高了5%～10%，立体错层开发取得较好的开发效果。图15显示了第1年的压力场，除了个别压裂段，在平面和纵向上井间均发生了较为显著的压窜，说明存在较为严重的裂缝重叠，即使采用交错部署的模式也导致在很短的时间内井间发生相互干扰，制约了气井产能的发挥，证明了目前水平井设计和压裂工艺条件下，压裂规模（裂缝高度、裂缝长度）过大，井距与压裂缝不匹配。

图15 井间干扰下的压力场图

3.2 人工裂缝与井距匹配关系

在目前井距和压裂规模条件下，重新设计压裂方案，模拟结果如图16所示。由图16可以看出，优化各井裂缝长度明显减小，靶体位于上部的井2（绿色）与其余2口井间的压窜程度降低。重新统计各井（支撑）裂缝模拟结果，其中井1裂缝为156簇，平均支撑裂缝高度为14.20 m，平均支撑裂缝长度为201.09 m，平均导流能力为125 mD·m；井3裂缝为58簇，平均支撑裂缝高度为15.78 m，平均支撑裂缝长度为178.87 m，平均导流能力为305 mD·m；井2裂缝为32簇，平均支撑裂缝高度为16.33 m，平均支撑裂缝长度为212.70 m，平均导流能力为167 mD·m。在控制裂缝长度、裂缝高度的基础上，通过增加裂缝段数，保证了缝网与地层的接触面积，同时大概率避免了平面和纵向上的井间压窜，也增加了缝网内的导流能力。

图16 压裂方案优化前后人工裂缝分布图

图17为压裂优化方案后的区块生产动态。图17-a中，当气井单独生产时，由于缝网产能指数得到了提高，优化后的3口井单井EUR较原方案分别增加了14.7%、3.7%和7.6%；当3口井同时投产时，单井井间干扰率较原方案显著下降，区块累计产气量较原方案增加了0.49×108m3。图17-b显示了第1年末的井组压力场，表明井间未发生大面积压窜，井间干扰程度得到了较好控制，井组开发效果良好。

图17 优化方案下区块生产动态模拟图

对优化前后方案中3口井的人工裂缝长度做统计分析，取累计概率（CDF）80%～90%对应值作为合理井距区间。人工裂缝长度概率及累计概率如图18所示，从图18可以看出，原方案中合理井距介于375～455 m，远高于实际约300 m的井距（对应累计概率约为60%），这意味超过40%的裂缝超过井距发生压窜；优化方案对应的合理井距介于280～320 m，与实际井距相符，其较好的开发效果也证实了压裂设计与井距匹配性。由此可知，通过平衡裂缝、地层接触面积、井间干扰、裂缝与地层流入流出动态关系能够保证井组开发效果。

图18 人工裂缝长度概率及累计概率图

3.3 压裂—井距优化建议

川南地区储层分布与美国不同，美国二叠系盆地中多套层系纵向间距较大（超过100 m），而且层系间经常存在阻碍裂缝延伸的硬地层[35]，因此，不同层系井组间发生纵向裂缝干扰的几率很低[36]，这也是美国能够实施立体加密井网的前提条件。相比之下，川南地区目前开发优质页岩层段为同一层系（主要集中在五峰组—龙一1亚段），厚度介于20～35 m[17]，受裂缝高度延伸和支撑剂沉降影响，单套井网难以控制整个优质层段。

当部署上、下两套井网时，考虑到有限的纵向空间，遵循纵向错层、减小井距、控制靶体钻遇率的原则，贯彻拉链式压裂（形成平面交错裂缝）、细分切割（增加段数、簇数）、大规模压裂（提高加砂强度、用液强度）相结合的压裂设计理念，追求“多裂缝、短缝长、低缝高、高导流”的造缝效果，在立体储量联合动用前提下尽量降低上、下井组间压窜的可能性。同时生产过程中应采用单井全程控压生产制度[30,37]，在保持裂缝长效开启的同时，提供气井生产驱动力，提高单井可采储量，最终实现提高立体井网的开发效果。

4 结论

1）目标地层内不同层位内的水平井靶体均具有裂缝延伸和产能潜力，同层部署时井网难以动用整个纵向储量，立体部署能够大幅度提高整体储量动用程度。

2）部署立体井网时，通过调整水平井靶体层位，一定程度上缓解同层部署时的强井间干扰，在小井距条件下立体井网开发效果更好。

3）建立合理井距与人工裂缝匹配模式，在确保缝网与地层接触面积基本稳定的基础上，通过提高缝网内部导流能力进一步提高立体井网开发效果。

4）川南地区适宜采用错层开发的小井距模式，上、下两套井网分别部署于1号层位和层位4号层位，辅以平面交错布缝和纵向靶体交错部署的模式，形成“短缝长、低缝高”的造缝效果，井组采收率预计可提高5%～10%。