牵引齿轮裂纹对机车齿轮箱箱体振动影响的仿真分析*

许思思, 黄冠华

(1.中车工业研究院有限公司，北京 100070； 2.成都西交金测智能科技有限公司，四川 成都 610037)

0 引 言

近些年，状态修成为铁路领域热门研究课题，被应用部门高度重视。在状态修的实施过程，部件的日常状态是维修决策的重要参考[1]。重载机车由于运行载荷大，运行环境恶劣，因而传动系统部件的失效和故障时有发生，在这些故障中，齿轮裂纹故障是常见的故障之一[2-4]。机车齿轮通常封闭在齿轮箱里面，齿轮箱与构架进行弹性悬挂连接，因而检测的方式手段具有局限性，难以掌握齿轮的状态。尤其裂纹的萌生发展过程往往难以发觉，具有很强的隐蔽性。因此，研究齿轮系统故障状态与齿轮箱的振动关联性对于齿轮传动系统的状态监测具有重要的实际意义。

齿轮系统是常见的机械系统，对于齿轮系统动力学，众多学者已进行了大量的研究[5]，其中包含了齿轮裂纹故障下动力学性能研究在内的众多成果[6-7]，这些研究的主要对象基本都是针对齿轮系统自身。对于机车这样移动的、复杂的和强激励环境下的系统，现有的研究考虑的都是齿轮正常啮合情况下的振动响应研究[8-9]，齿轮裂纹故障下对箱体振动影响的研究较少。

笔者基于仿真技术，首先通过有限元法获取齿轮系统在无裂纹和裂纹故障下的时变啮合刚度，然后将得到的齿轮啮合刚度导入齿轮动力学模型，得到车轴和齿轮箱的等效支撑力。最后通过多体动力学软件SIMPACK提供的表达式接口进行联合仿真，实现齿轮裂纹状态下的齿轮箱箱体的振动影响分析。

1 齿轮系统有限元模型

鉴于目前齿轮传动系统动力学模型研究已经较为成熟，文中的研究重点是得到齿轮裂纹时的变化啮合刚度。通过三维造型软件建立齿轮实体模型，再导入至有限元工具ANSYS中，进行仿真分析计算。为了提高计算效率，只保留少部分轮齿。在图1中，左边大齿轮是从动轮，右边小齿轮为主动轮，大小齿轮分别施加转矩和约束。图1是建立好的机车齿轮副有限元模型，网格划分后，共得到62 080个单元，241 375个节点。齿轮材料参数见表1。

图1 齿轮副有限元模型

表1 齿轮具体材料参数

2 啮合刚度计算

通过仿真求出齿轮轴转角，进而可求出齿轮啮合刚度。齿轮啮合刚度计算公式为：

k=T/(Δθr2)

式中：T为齿轮轴转矩；Δθ为齿轮轴转角；r为轴半径。

为了得到齿轮裂纹工况下齿轮啮合刚度曲线，基于上述有限元模型，在牵引主动齿轮根附近分别设置宽1 mm深2 mm、宽1 mm深4 mm和宽1 mm深6 mm裂纹并进行有限元分析，从动齿轮保持正常，具体设置示意图如图2所示，得到不同工况下的啮合刚度曲线如图3所示。

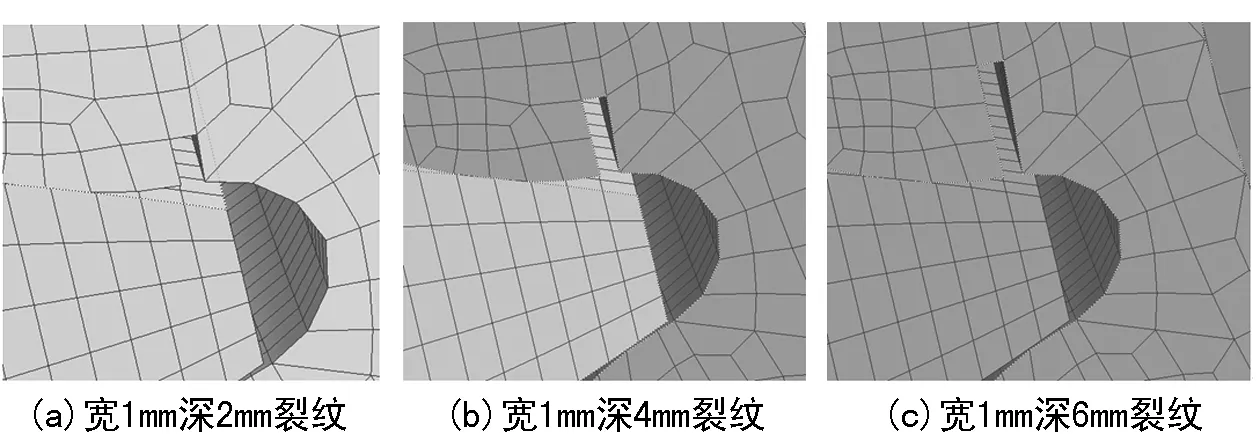
图2 齿轮不同裂纹深度

图3 牵引齿轮正常和不同裂纹状态下齿轮啮合刚度

3 机车动力学模型

以C0-C0电力机车动力转向架为研究对象。利用多体动力学软件SIMPACK，首先建立机车斜齿轮传动系统模型。裂纹引起的齿轮间的啮合刚度和相互作用通过前述的分析中进行导入，可视化模型如图4所示。与此同时，整车动力学模型还包括电机、轴箱、构架和车体，整车动力学可视化模型如图5所示。

图4 齿轮传动系统模型

图5 机车整车动力学模型

4 分析计算

为了获取箱体在主动轮裂纹下的振动性能，利用上述建立的整车动力学模型进行仿真，设置仿真条件扭矩为3 000 N·m，车辆运行速度80 km/h，牵引齿轮裂纹深度(0 mm、2 mm、4 mm、6 mm)。

通过动力学仿真获取主动轮裂纹不同深度状态下箱体的振动加速度时域信号，如图6所示。

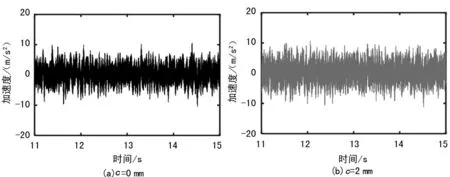
图6 不同裂纹深度下箱体垂向加速度时域图

可以看出，当主动轮出现裂纹时，箱体的垂向振动加速度时域曲线出现一定程度的变化，当裂纹深度c=6 mm时，箱体的振动加速度冲击增大，幅值也有所增加，然而小裂纹情况下不容易直接捕捉箱体的振动响应变化。

为了进一步获取主动轮裂纹作用下箱体的振动特征，基于上述数据，计算时域统计指标，主要包括有量纲统计指标和无量纲统计指标。箱体振动加速度有量纲统计指标见表2。可以发现，随着主动轮裂纹深度的增大，有量纲指标有一定程度的增大。当裂纹深度c=4 mm时，平均幅值、方根幅值、标准差、有效值、峰峰值分别增加10.88%、7.62%、15.52%、15.52%、49.66%。当裂纹深度c=6 mm时，上述五个指标分别增加了41.54%、36.02%、50.02%、50.01%、78.11%。

表2 有量纲统计指标 m/s2

箱体振动加速度数据无量纲统计指标见表3。当齿轮出现裂纹时，部分无量纲统计指标均一定程度的增加。当裂纹深度c=4 mm时，与正常齿轮振动加速度相比，峭度指标、峰值指标、脉冲指标、波形指标、裕度指标分别增加21.44%、35.46%、41.12%、4.18%、45.40%，但偏度指标增加不明显。裂纹深度c=6 mm时，上述五个指标分别增加34.28%、19.91%、27.09%、5.99%、32.25%，但偏度指标增加不明显。通过以上分析可知，当主动齿轮出现裂纹时，有量纲统计指标和无量纲统计指标均有所增加，选择合适的统计指标可以在一定程度上反映主动轮存在裂纹时所引起的箱体的失效特征。

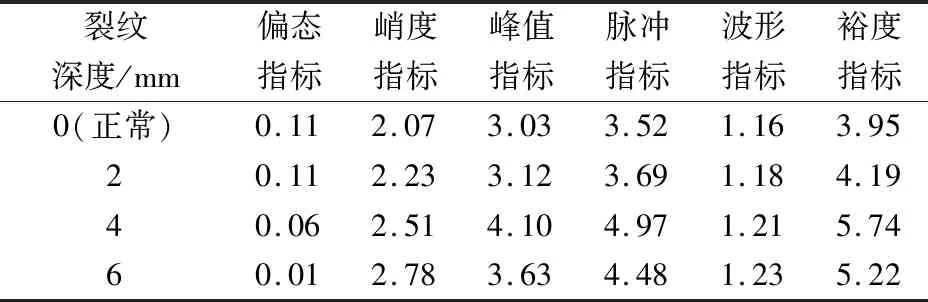
表3 无量纲指标

为了进一步分析主动轮裂纹状态下箱体的振动特征，对前面获取的加速度时间历程曲线进行频域分析，采用快速傅里叶变换方法，得到了主动轮裂纹故障下箱体的振动加速度频谱结果，不同裂纹深度下的频谱如图7所示。可以发现，所有工况中均出现了593.9 Hz的啮合频率。另外，出现了由轨道不平顺引起的低频成分。频谱图的局部放大图如图8所示。

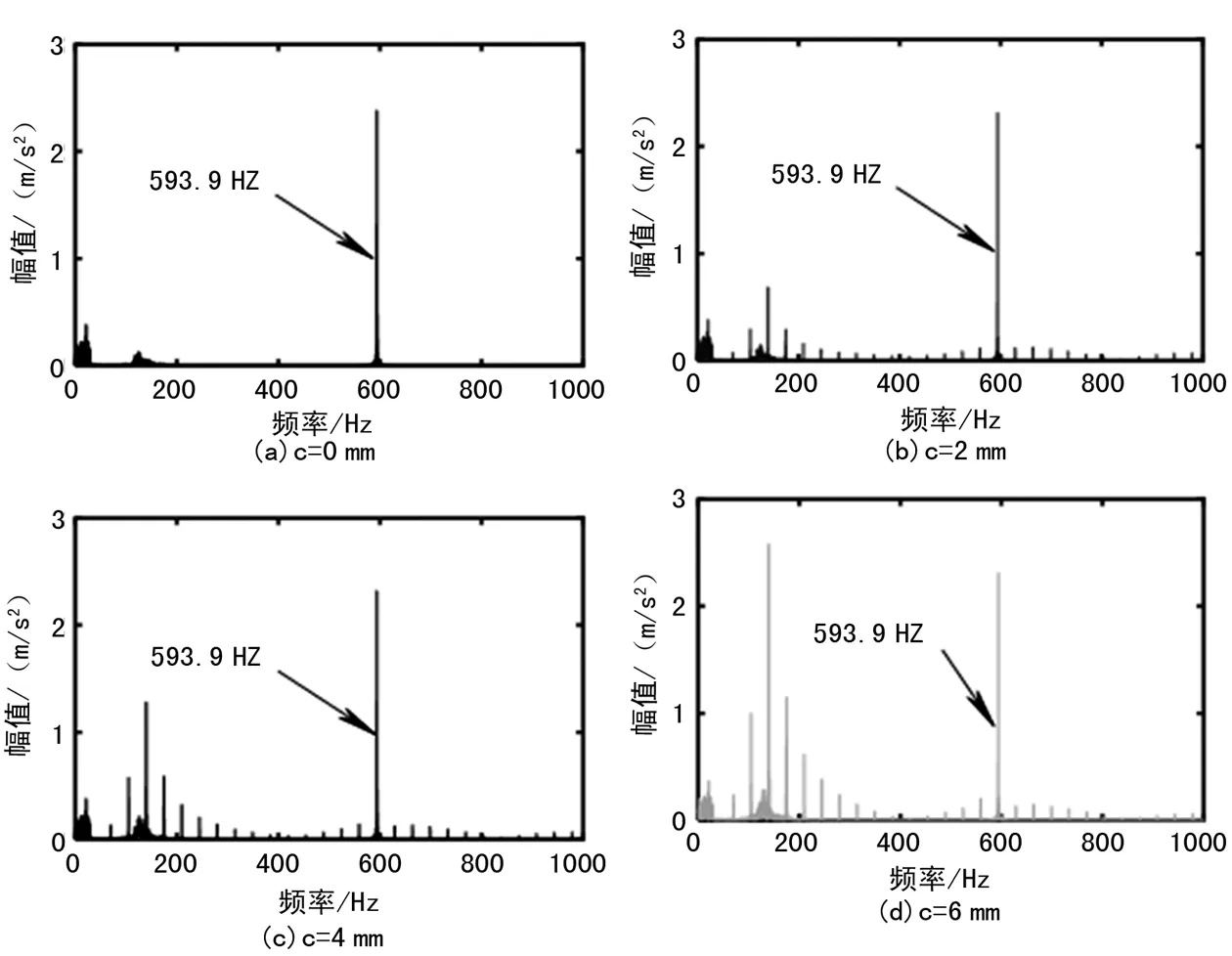
图7 不同裂纹深度下箱体垂向加速度频域图

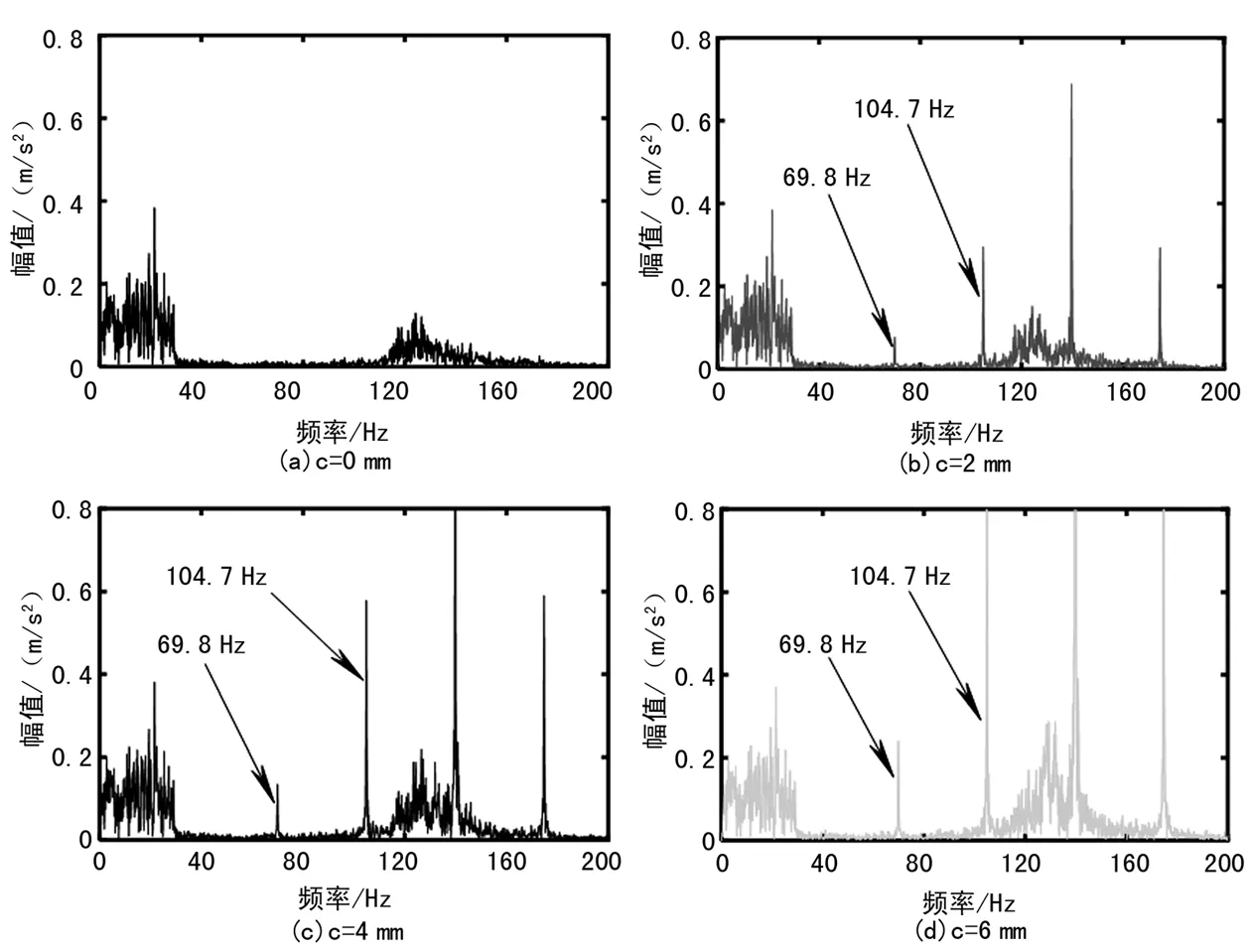
图8 频谱图的局部放大图

可以看出，当主动轮出现裂纹时，振动加速度频谱图同时出现转频34.9 Hz及其倍频。在进行故障诊断时，需要对箱体的频率成分进行详细分析，以推断齿轮系统是否发生故障。

5 结 论

通过建立的考虑牵引齿轮裂纹的齿轮系统模型和机车整车动力学模型，分析了正常工况和牵引齿轮裂纹工况下齿轮箱箱体的振动响应变化，得到以下结论。

(1) 发生齿轮断裂故障时，齿轮箱箱体的振动加速度响应增加，增加的幅值和裂纹的大小相关。裂纹深度小于4 mm时，增加的幅度并不明显，裂纹深度为4 mm时，有效值和峰值的增幅分别达15.52%和49.66%，裂纹深度为6 mm时，有效值和峰值的增幅达50.01%和78.11%。无量纲指标中的峭度指标、峰值指标、脉冲指标、波形指标、裕度指标也有明显增加。

(2) 轮齿正常啮合时，啮合频率是齿轮箱箱体响应频谱中的主频，发生齿轮裂纹故障时，牵引齿轮的转频及其倍频，齿轮啮合频率，箱体的悬挂频率在频谱的主频中都能明显地被观察到。

(3) 在机车智能运维状态监测中，可以通过监测齿轮箱箱体的振动响应来分析特征频率，进而判断是否发生齿轮裂纹的故障，为车辆的安全状态检测提供有效建议。