弹性边界下局部涂覆约束阻尼梁的振动特性研究*

林 丽,谢宇航

(大连交通大学 机车车辆工程学院，辽宁 大连 116028)

0 引 言

振动现象广泛存在于人们的生产生活中，振动与噪声能够影响结构的安全性、耐久性、舒适度以及人体的健康，因此结构的减振降噪已成为研究的热点问题[1]。粘弹性材料应用于减振、降噪技术已经有几十年的发展历史，由于它在减振降噪方面表现出的良好效果，因此受到了广泛重视。但是粘弹性材料的弹性模量都比较小，通常要比常见金属弹性材料要低四个数量级以上，所以一般不能单独成为工程中的结构材料，而是将它粘附在需要作减振降噪处理的机械结构或工程结构构件上，常用措施是在粘弹性材料上面再附加一层弹性材料(称为约束层)，一起构造约束阻尼结构[2]。粘弹性材料由高分子聚合物组成，它有较高的耗能模量，能在相当宽的频带内抑制振动和噪声。当粘弹性层随基本结构一起产生弯曲振动而使粘弹性层产生拉压变形时，在粘弹阻尼材料内部会产生剪切应变，从而将振动能转变为热能耗散掉。而约束层的加入会增大粘弹性层的剪切变形从而耗散更多的振动能量[3-4]。对于梁结构，很适合用约束阻尼结构的方式来进行减振降噪处理，如果约束层的材料为普通弹性材料(一般为金属)，则这种夹层梁结构被称为被动约束层阻尼(PCLD)梁[5]。

由于考虑到阻尼材料成本、重量和耗能效率，同时也为了增强工程实用性，因此，只有部分基础结构被PCLD覆盖的地方使用阻尼处理显然更实用。关于局部约束阻尼的研究最早可追溯到1968年，由Nokes和Nelson给出了有关解决部分覆盖的约束阻尼梁问题的研究[6]。1988年，Lall等人[7]探讨了部分覆盖夹层粱对固有频率与损耗因子的影响。Ravi等[8]应用模态叠加法研究了两端固定的局部或全部敷设自由阻尼层和约束阻尼层梁的动态响应。石慧荣[9]针对局部敷设被动约束阻尼简支梁进行力学分析。

从文献中不难看出这些研究大都基于经典边界，即简支、固支、自由边界以及他们的组合。但是由于实际的梁结构边界约束条件相对复杂，导致梁结构的阻尼特性及其对结构振动特性的预测与实际性能存在一定的差距。因此，笔者基于一阶剪切变形理论的基础上，提出了一种简单、便捷、有效的评估弹性边界下局部涂覆约束阻尼梁振动特性的分析模型。并通过文中计算结果与现有公开文献数据和有限元计算结果进行对比，验证文中方法的正确性和可靠性。并对涂覆率对减振性能的影响进行讨论。

1 理论与方法

1.1 基本假设

为了便于计算分析，提出下列基本假设条件。

(1) 基梁和约束层按Timoshenko梁处理。

(2) 不考虑垂直于板面方向的压缩变形，认为基层、阻尼层、约束层有相同的挠度函数。

(4) 忽略各层转动惯量的影响。

(5) 粘弹性层仅在线粘弹性范围内讨论。

(6) 各层材料之间完美粘贴，层间无相对滑移。

1.2 模型介绍

局部涂敷被动约束阻尼(PCLD)梁结构如图1所示。其中，基梁长度为L，宽度为B。以基梁左端中点为原点建立坐标系OXZ，基梁、粘弹性层和约束层的位移可表示为：ui(x,z,t)，wi(x,z,t)；截面转角为：φi(x,z,t),(i=b,v,c)。坐标归一化η=x/L。

图1 局部涂敷PCLD梁结构示意图

基于一阶剪切变形理论，轴向位移u和横向位移w可表示为：

(1)

式中：ui和w分别是梁域中任意点沿x和z方向的位移；ui,0被定义为在中间表面的位移。根据上述位移场，结构应变位移关系表示为：

(2)

则应力应变关系表示为：

(3)

式中：κi为剪切系数，对于矩形截面梁，由以下公式表示：

(4)

式中：μ为泊松比。

对于粘弹性材料，其位移场可通过基梁和约束层的位移表示出来。图2为各层变形示意图，由位移连续性条件，对于截面1和2，可分别得到如下等式：

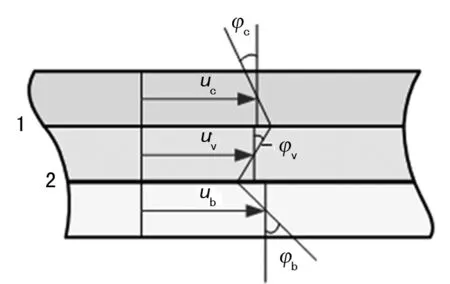
图2 层间位移连续性条件

(5)

式中：hb,hv,hc分别为基梁、粘弹性层和约束层的厚度，由上式可以解得：

(6)

基梁的应变能和动能为：

(7)

约束层的应变能和动能为：

(8)

阻尼层应变能和动能：

(9)

文中通过引入边界弹簧技术来模拟一般弹性边界条件，因此在计算时要将储存在这些弹簧中的弹性势能考虑在内。此处针对满铺情况，考虑在三层结构上都加弹簧，若为局部涂覆PCLD梁，边界弹簧应仅施加到基梁上，此时只需考虑式中的前两项：

(10)

外力作用的虚功为：

(11)

1.3 容许函数

在瑞利-里茨方法中，选择合适的容许函数是至关重要的，因为容许函数的选择决定了精度和收敛性解决方案的重要性。在这里选用正交多项式，正交多项式形式的纵向模态函数可表示为：

(12)

1.4 动力学方程

根据得到的能量表达式和容许函数，构建拉格朗日量：

L=T-U=(Tb+Tv+Tc)-(Uε,b+Uε,v+

Uε,c+Usp)

(13)

带入拉格朗日方程：

(14)

可得到动力学方程：

多数黄瓜品种在8～11 h的短日照条件下生长良好。适宜的温度是保证黄瓜生长的基础与前提，黄瓜喜温暖，不耐寒冷，最适宜地温为20～25℃，最低为15℃左右。黄瓜喜欢潮湿的环境，栽培过程中要求保持水分充足，适宜土壤湿度为60～90%，适宜的空气相对湿度为60～90%，光照充足条件下可以适时提升土壤湿度。另外，黄瓜喜肥而不耐肥，要求结合黄瓜生长状态选择施肥，宜选择富含有机质的肥沃土壤。同时合理控制土壤的pH值，通常pH值控制在6.5为宜，以保证黄瓜健康生长。

(15)

其中：

q={(qub)T,(qφb)T,(quc)T,(qφc)T,(qw)T}T

(16)

1.4.1 固有特性求解

令公式(15)右侧为0，设q=q0eiωt，得到特征值方程：

(-ω2M+K)q0=0

(17)

(18)

1.4.2 谐响应求解

在施加横向定频点激励的情况下，式中的fw(η,t)可表示为：

(19)

式中：η*为激励点位置；Ω为激励频率。

则此时广义力的虚功为：

=ejΩtδw(η*,t)

(20)

广义力：

(21)

(22)

(23)

2 数值分析

2.1 模型验证

为了验证文中方法的正确性，引入一个算例[10]，将文中的计算方法、算例文献计算结果和基于有限元分析的计算结果进行数据对比。算例中材料和结构参数如表1所列。

表1 PCLD梁结构的材料和结构参数

文中通过引入边界弹簧技术来模拟复杂边界条件，通过对边界弹簧的刚度赋予适当的值，可以很容易地实现经常遇到的各种边界条件。除了经典边界外文中又考虑了四种复杂边界条件，分别用符号E1、E2、E3和E4表示。表2所列给出了经典边界和弹性边界的相应弹簧刚度值。

表2 不同边界条件下对应的弹簧刚度值

表3和表4分别列出了本方法对固支-自由边界的PCLD梁结构前6阶固有频率和损耗因子的预测结果及算例文献计算结果和基于有限元分析的计算结果的数据对比。为了确保结果的可靠性，分别对粘弹性材料损耗因子取值0.1和1.5两种情况下的结果进行对比。通过对比分析发现，采用文中方法所得的计算结果与相关文献吻合度十分良好。因此证明了文中方法具有良好的预测精度。通过本小节的研究也证明了该方法具备处理弹性边界局部涂覆约束阻尼梁振动特性的能力。

表3 C-F边界PCLD梁固有频率对比

表4 C-F边界PCLD梁损耗因子计算值对比

2.2 参数化研究

为了探究涂覆率对减振性能的影响，以固支-自由边界的PCLD梁为研究对象，其材料和结构参数如表1所示。激励点设置在x=L/2处，分别求出涂覆率为50%，75%，100%时，在x=L处w方向位移幅频曲线。敷设形式采取按以梁中点对称敷设，简谐力载荷振幅为1 N，频率在1～800 Hz范围内变化。

综合图3～5可以观察到，减振效果总是随着PCLD梁涂覆长度的增加而增加。但是，当涂覆长度增加到一定程度后，进一步增加覆盖面积则会降低减振效果。也进一步说明了，局部涂覆的PCLD梁更具有实际工程意义。

图3 50%涂覆率的PCLD梁位移幅频

3 结 论

(1) 文中在能量法的基础上推导了局部涂覆约束阻尼梁振的运动控制方程，并采用假设模态法求解。通过模型验证，证明了该方法具有良好的收敛特性和计算精度。

(2) 当边界条件发生变化时，仅仅修改边界参数即可，而不需要重新推导；同时，通过对x1,x2赋予不同的值可以轻松改变涂覆的位置和面积，总体而言该模型简洁又高效。

(3) 减振效果随着涂覆率先增大后减小，也说明了局部约束阻尼结构可以减轻构件质量，达到更好的减振效果，降低了成本，应用灵活。