基于低秩稀疏分解的采煤机轴承复合故障分离

包从望，江伟，郭灏，刘永志

（六盘水师范学院矿业与机械工程学院，贵州 六盘水 553000）

采煤机作为煤矿生产的关键设备，其工作条件恶劣，运行过程中存在诸多不可控因素，受变速、变载的复杂冲击载荷影响常出现轴承破损故障，从而诱导采煤机其余关键部件受损，甚至可能引起人员伤亡事故。随着深部煤层智能开采装备的发展，对采煤机轴承故障的智能诊断提出更具挑战性的要求，研究恶劣工况下采掘装备的故障智能辨识，实现故障实时监测与预警，是智能开采的突破方向之一。采煤机截割部的轴承是关键的传动支撑部件，受信号混叠的影响，难于从混合信号中提取轴承的故障信号，为此采煤机轴承复合故障的有效分离，是实现轴承运行状态监测的前提［1］。

盲源分离方法可在源信号未知及混合成分未知的情况下将源信号分离，随数字信号处理技术的发展，目前已成为有用信息提取的主要途径之一。王奉涛等［2］将振动信号进行经验模态分解（empirical mode decomposition，EMD）后，以峭度等指标作为信号重组依据，利用核主成分分析提取流行成分，并在快速独立成分分析（fast independent component analysis，Fast-ICA）算法下实现源信号的还原。郝尚清等［3］将信噪比的最大值作为目标函数，进行盲源分离，进一步提取采煤机摇臂轴承的故障特征。Zhen等［4］基于稀疏编码技术，利用分层聚类方法获取混合矩阵估计，最后通过求解一序列最小二乘问题，实现源信号的分离。朱将涛等［5］引入广义时间窗重构空间矩阵，并将其奇异值进行动态聚类，利用自适应Parafac方法实现采油机轴承故障的盲源分离。李国正［6］基于稀疏策略算法，结合支持向量机（support vector machine，SVM）构造了高纬估计混淆矩阵，实现基于能量法的盲源分离模型。低秩稀疏分解理论由Donoho等［7］提出，可滤除干扰噪声后提取信号中的微弱信号。陈礼顺等［8］依据观测信号中的干扰和特征信息的奇异值分布建立奇异值低秩稀疏先验，基于广义块的模型求解框架实现了锥齿轮的故障诊断。Wei等［9］采用分裂增广拉格朗日收缩算法实现稀疏表示，基于最优小波原子实现齿轮箱故障特征的提取。Zhi等［10］利用基于均值的奇异值分解提取复杂信号的潜在成分，利用稀疏表示实现背景噪声的抑制，从而提取行星齿轮的故障特征信息。

为实现采煤机轴承复合故障的快速、高效诊断，本文提出一种基于低秩稀疏分解的采煤机复合故障分离方法。首先，利用低秩稀疏分解将混合信号分解为低秩组分和稀疏组分，通过Fast-ICA从低秩组分中分离出特征较明显的故障信息；其次，应用EMD将稀疏组分解为多通道内涵模态函数，并进一步提取微弱的故障信息，从而实现复合故障的分离。

1 理论基础

1.1 低秩与稀疏分解

低秩稀疏分解的实质是将具有一定相关性的信号矩阵转换为低秩矩阵和稀疏矩阵，表达式如下：

式中：D为被分解的轴承振动信号矩阵；A为分解后的低秩矩阵；E为稀疏矩阵。

其求解的过程为一个凸优化的过程，表达式如下：

式中：λ为非负权重参数；r(A)为矩阵的秩函数；||E||0为矩阵的泛数，即秩函数的凸包。

利用矩阵的l0范数对稀疏性进行约束，将式（2）转换为凸优化的求解模型，表达式如下：

利用增广拉格朗日函数求解该优化问题，其函数表达式如下：

式中：Y为拉格朗日乘子，初始值取为0；c为正则化系数；μ为大于0的惩罚系数，初始值取2/3；·为信号矩阵的内积；||·||F为F范数。

低秩和稀疏分解优化的收敛条件如下：

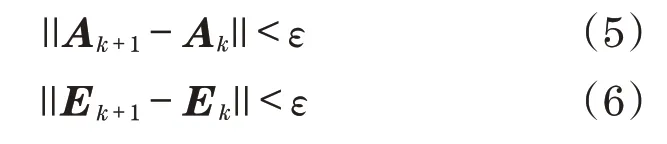
式中：ε为收敛精度。

输入观测轴承观测矩阵D，其求解步骤如下：

步骤1初始化式（4）中的参数；

步骤2根据式（5）、式（6）分别判定低秩部分和稀疏部分是否收敛，若收敛，则直接输出结果，若不收敛，则进入到步骤3；

步骤3对式（D-Ek+Yk/μk）进行奇异值分解，结果分别为U、S、V；

步骤4进一步计算Ak+1、Ek+1、Yk+1：

步骤5更新惩罚系数μk+1=ρμk，k=k+1，返回至步骤2，满足收敛条件，则输出；

输出A、E。

1.2 Fast-ICA盲源分离算法

为实现轴承的复合故障诊断，采用盲源分离方法实现轴承多源故障信号的分离。在众多盲源分离理论中，独立主成分分析（independent component analysis，ICA）因其基于信息准则的优化和统计学的代数算法，具有良好的收敛效果和收敛速度，备受关注。

将M个源信号表述为x（t）=［x1（t），x2（t），…，xM（t）］，N个测量信号表述为y（t）=［y1（t），y2（t），…，yN（t）］。将M个源信号混合后利用传感检测获得N个观测信号，对应的关系式如下：

式中：A为未知的混合矩阵。

ICA方法的宗旨就是将N个观测信号分离为M个源信号，设还原后的信号为Y（t）=［Y1（t），Y2（t），…，Yn（t）］，则关系式如下：

式中：Y为源信号的近似估计；W为分离矩阵。

在ICA算法中，Fast-ICA以批量处理的方式进行寻优迭代，迭代过程中每次都有大量样本进行计算，收敛速度优于其他ICA算法。其计算步骤如下：

步骤1信号预处理。信号中心化，即将信号矢量减去均值，此时的均值变为0；白化处理，去除信号间的相关性，简化独立成分的提取过程，提高收敛性，白化后得到v。

步骤2选择需要的独立分量个数m，设定迭代次数和具有单位范数的初始权矢量wp，其计算式如下：

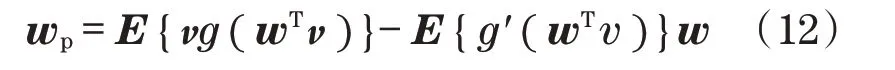
式中：g为非线性函数，其计算式如下：

步骤3更新wp后将其标准化为wp=wp/||wp||，判断是否收敛，若不收敛，则返回步骤2。

2 基于低秩与稀疏组分轴承复合故障分离方法

信号经低秩和稀疏分解后得到低秩组分和稀疏组分，从低秩组分中可获取故障信号的结构特征，稀疏组分中不仅包含干扰信息，还包括部分被干扰噪声淹没、不易被Fast-ICA提取的故障信息。基于此，结合低秩稀疏分解和盲源分离方法实现轴承的复合故障分离，如图1所示。

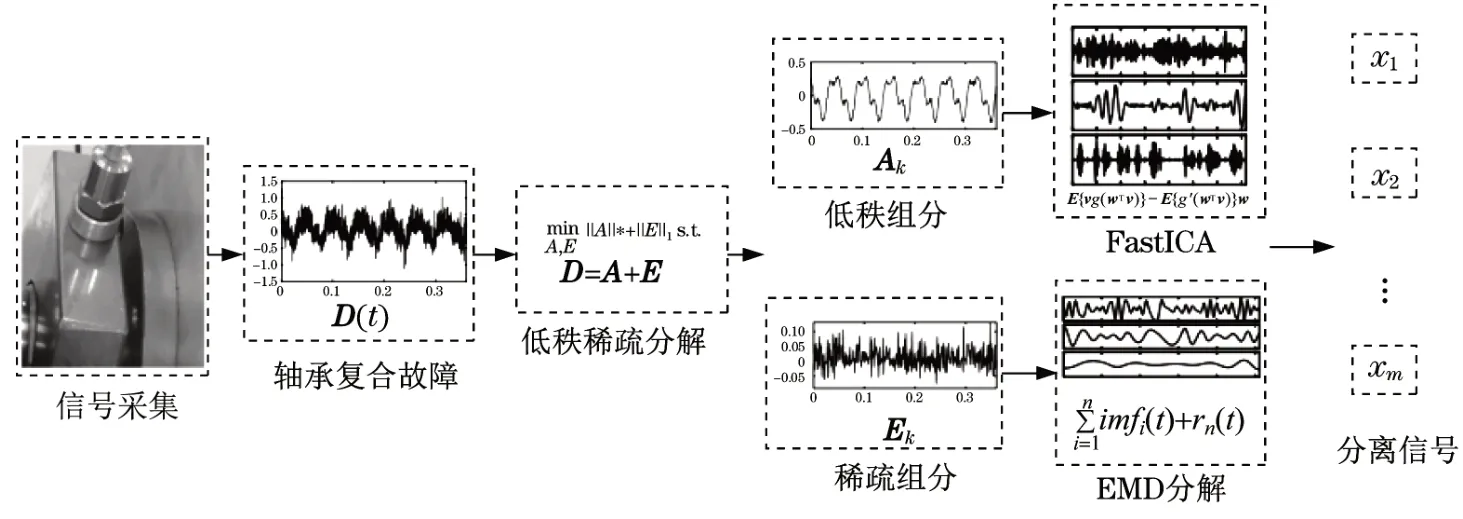
图1 基于低秩稀疏分解的故障分离方法Fig.1 Fault separation method based on low-rank sparse decomposition

具体步骤如下：

步骤1将各个观测信号作低秩稀疏分解后，获得低秩组分Ak和稀疏组分Ek；

步骤2利用Fast-ICA将低秩组分Ak分离为一组源信号x1（t），x2（t），…，xi（t）；

步骤3为进一步将稀疏组分中的干扰信息与故障信息分开，以增加有利于识别的故障特征，利用EMD分解将稀疏组分分解为频率成分不同的内涵模态函数，并将其作为另一组源信号xi+1（t），xi+2（t），…，xm（t）。

3 数据集仿真与应用

根据轴承故障位置，可将轴承故障分为轴承外圈故障、轴承内圈故障和滚动体故障。为验证算法的有效性，基于凯斯西储大学的轴承故障信号，分别验证只有一种故障和存在两种故障状态时的诊断效果，其中，验证单一故障的目的为检验混合故障诊断模型是否会出现误判。

选取型号为NTN6205的深沟球轴承，当滚动体故障直径为0.7112 mm、故障深度为3.81 mm、驱动电机功率为735.5 W、转速为1772 r/min、采样频率为12 kHz时，对应的时域波形中能明显地看出存在周期振动信号。

对时域信号作低秩稀疏分解后得到低秩组分和稀疏组分，时域波形如图2所示。从仿真图中可知，低秩组分包含了明显的故障信息，稀疏组分中存在一定故障特征频率，且包含了噪声干扰，因此周期振动的显著程度不如低秩组分，有待进一步作分解。

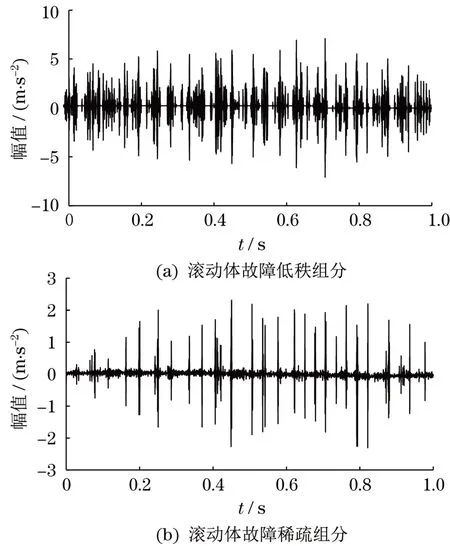
图2 滚动体故障时低秩组分和稀疏组分时域图Fig.2 Time domain diagrams of low-rank and sparse components under rolling failure

将低秩组分输入到Fast-ICA中，将其分离为源信号之一，如图3所示，分离后的信号存在更为明显的故障特征。利用快速傅里叶变换将其转换为时频特征，如图4所示，2个分离的源信号中明显的故障频率分别为139.30、137.20，均与滚动体故障频率139.05 Hz接近。除此之外，还分别包含30.60、29.80 Hz的特征频率，与转动轴的基本频率接近。

图3 滚动体故障时低秩组分分离结果Fig.3 Results of low-rank component separation during rolling failure

图4 滚动体故障时低秩组分分离结果频谱图Fig.4 Spectrum diagram of low rank component separation results under rolling failure

为进一步挖掘稀疏组分中所涵盖的故障信息，将稀疏组分作EMD分解，得到各个内涵模态分量如图5所示。各分量中包含明显的周期振动信息，为进一步提取故障频谱信息，采用傅里叶变换求解各分量的频域特征如图6所示。由稀疏组分的IMF分量频域特征可知，IMF0中主要频率成分为138.4 Hz，与滚动体故障对比后发现该方法可以进一步有效提取滚动体重微弱的故障信息。其余IMF分量中存在一定的明显故障信息，但随着阶次的上升，幅值呈下降趋势，故可将其舍去。

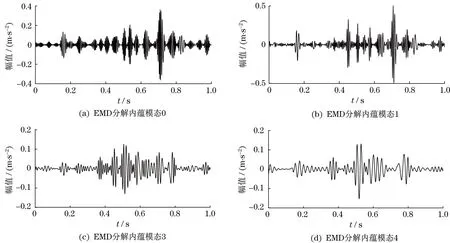
图5 滚动体故障时稀疏组分EMD分解结果Fig.5 Results of sparse component EMD decomposition under rolling failure

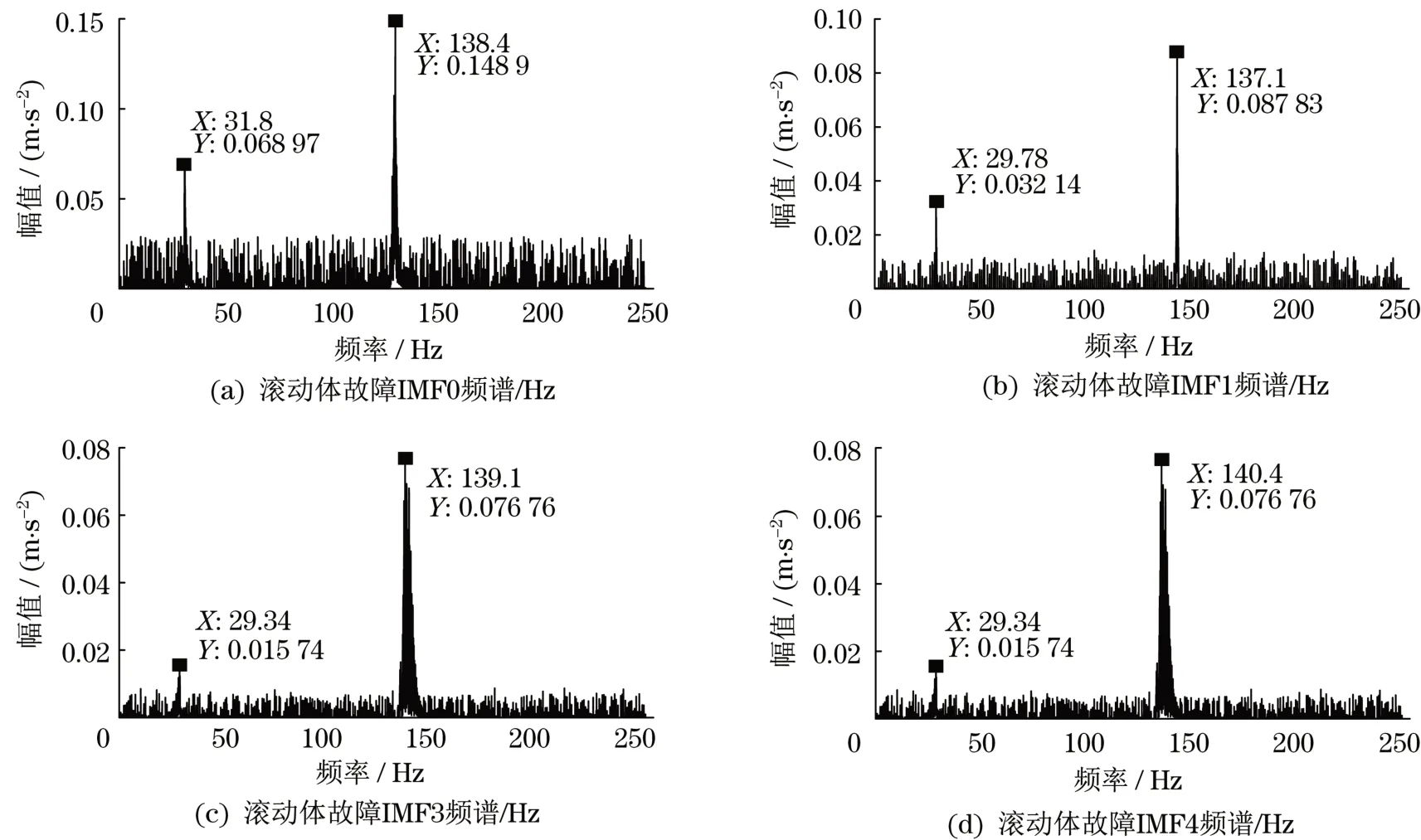
图6 滚动体故障时稀疏组分IMF频谱Fig.6 The IMF spectrum is sparse when the rolling body fails

为验证轴承存在复合故障时的诊断效果，举例轴承既有滚动体故障，又有外圈故障时的诊断。分别取驱动端和风扇端的轴承故障信号作为复合故障信息，两端轴承型号分别为SKF6205和SKF6203，故障类型分别为滚动体故障和外圈故障，故障直径为0.3556 mm，深度为0.2794 mm，转速均为1750 r/min，估算外圈故障频率为89.1 Hz，滚动体故障频率为137.5 Hz。将两种故障信号进行叠加混合后作为复合故障分离的目标信号，比较混合前后的故障信息发现，当同时存在滚动体故障和外圈故障时，滚动体故障信息基本被外圈故障覆盖，难以显现。

基于所提方法，对混合信号进行低秩稀疏分解，并将低秩组分分离为源信号后对其进行频谱分析，得到低秩组分分离信号的频谱信息如图7所示，包含了3类明显频谱31.79、89.38、138.90 Hz，分别对应转轴频率外圈故障频率和滚动体故障频率，但滚动体故障特征明显低于外圈故障信息，容易被噪声淹没。为保证实际诊断过程中该故障信息不会丢失，对稀疏组分作EMD分解，得到IMF0的频谱信息如图8所示，IMF分量包含了滚动体故障和外圈故障的频率分别为91.15 Hz和137.00 Hz，与计算值接近，进一步验证信号中包含两种故障信息。

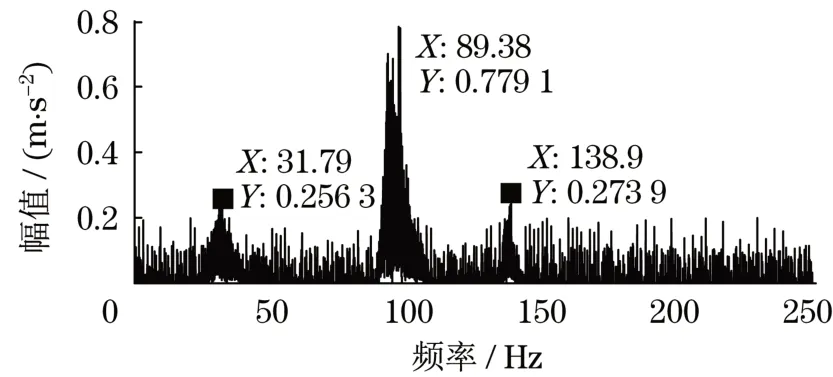
图7 低秩组分频谱图Fig.7 Spectrum diagram of low-rank components

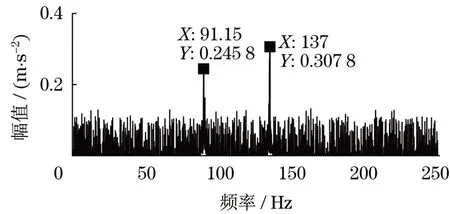
图8 稀疏组分频谱图Fig.8 Spectrum diagram of sparse components

4 实例应用

数据集仿真中的混合信号只是将两种故障信号相加，而采煤机在运行过程中可能会出现同一个轴承上同时存在两种故障，为验证所提方法的有效性和通用性，实验过程中采用NU202轴承进行现场实验验证，轴承的结构参数见表1。在实验中设定轴承内圈故障和滚动体故障，其故障尺寸均直径为0.4 mm，深度为0.5 mm。轴承外圈故意频率fo，轴承内圈故意频率fi，滚动体故意频率fr计算式为

表1 轴承结构参数Tab.1 Bearing structural parameters

式中：Z为滚子数量；d为滚子直径；D为节圆直径；fR为轴旋转频率；α为接触角。

设转轴频率为20 Hz，根据式（16）～式（18）计算轴承外圈、内圈和滚动体的故障特征频率分别如下：88.0、132.0、105.6 Hz。结合采煤机截割部的运行状况，当碰到坚硬的岩石时，截割力矩可能会迅速上升且转速降低，搭建采煤机轴承故障模拟实验台如图9所示，通过磁力加载器模拟采煤机截割部的截割过程，包含固定的截割力矩和随机性的冲击信号。

图9 截割部轴承故障实验台Fig.9 Bearing failure test bench at cutting part

采用TensorFlow搭建采煤机截割部轴承故障诊断系统。在轴承座上安装加速度振动传感器，调整变频电机的输出转速为1000 r/min，稳定载荷为400 N·m，同时随机加载600 N·m的冲击载荷。基础振动信号中蕴含着不同程度故障信号，为验证低秩稀疏下的复合故障提取效果，对信号进行低秩稀疏分解，得到低秩和稀疏组分。将低秩组分输入到Fast-ICA中，对低秩组分进行分离，得到其中一组分离信号的频谱如图10所示，其冲击频率分别为107.5、134.1 Hz。分别对应滚动体故障和内圈故障，可见分离信号能较好的将内圈故障分离，但滚动体故障偏微弱，容易被淹没而导致漏诊断。

图10 实验台低秩组分频谱图Fig.10 Spectrum diagram of low-rank components in the laboratory

利用EMD分解将稀疏组分分解为各个频率层次的内涵模态，各分量中均包含明显的周期振动特征。为进一步验证分量中是否包含轴承其余故障，取第一阶分量做频谱分析，其频谱结果如图11所示。从频谱图中可知，存在与轴承外圈故障和轴承滚动体故障频率接近的频率信息107.0 Hz和139.4 Hz，可据此进一步判断轴承外圈和滚动体均发生了故障，从而实现复合故障诊断。

图11 稀疏组分内涵模态的频谱信息Fig.11 Sparse components contain modal spectral information

5 结语

通过低秩稀疏分解，利用Fast-ICA将低秩组分分离为源信号，从源信号的频率冲击可以看出分离信号中可将各类混合故障反映出，但部分故障类型特征信息较弱。为进一步增强提取故障信息较微弱的故障类型，将稀疏组分分解为各频段的内涵模态成分，其频谱中可明显观测到微弱故障类型，克服了低秩组分中部分故障信息不明显的缺点，从而实现采煤机轴承故障的复合诊断。该方法能很好地实现采煤机轴承多源故障分离，可较精确地辨识多源轴承故障类型，为实现复合故障诊断提供方法指导。