单晶材料微磨削表面粗糙度模型预测与优化

孙杨，于联周，巩亚东

（1.沈阳城市建设学院机械工程学院，辽宁 沈阳 110167；2.东北大学机械工程与自动化学院，辽宁 沈阳 110819）

随着我国航空事业的快速发展，对航空产品所应用的材料和制造精度的要求越来越高，而航空发动机在高温环境下工作的特殊性，无论对在零件的制造工艺质量，还是高温环境下的稳定性都提出了更高的高求［1］。一些单晶材料应运而生，与多晶材料相比，镍基单晶材料具有耐高温、抗氧化和热疲劳性能优越等特点，而微磨削作为微加工的最后一道工序，可使工件表面获得良好的粗糙度，在制造精度上能达到微米级，不仅可以实现产品微小型的制作，而且可以获得质量更好的表面。由于微磨削要考虑到磨棒直径与磨削深度接近同数量级这一因素，这使微磨削与传统磨削在磨削机理上有不同之处。针对新兴材料与加工方法的不同，对单晶材料的微磨削表面粗糙度的预测不能再应用过往的传统预测模型，应建立单晶材料自身所具有的预测模型。因此，建立单晶材料微磨削表面粗糙度预测模型对实际应用具有重要的意义。

目前，国内外对材料加工表面粗糙度预测的研究取得了许多成果。上海交通大学李成锋［2］建立介观尺度铣削表面形貌预测模型，得到铣削表面质量与主轴转速和单齿进给率之间没有交互关系，而是单调变化。Lacalle等［3］研究了直径为100 μm微磨棒对硬钢微磨削，得到随着磨粒尺寸减小到1 μm，最终得到表面粗糙度为47 nm。Tsai等［4］研究了铣削薄板类零件，建立周铣削表面尺寸误差模型。

在所查阅的研究资料中，很少有针对单晶材料的微尺度磨削表面粗糙度的预测，并且对预测模型的研究单一，并未将多种方法相结合而获得优化的预测模型。综上所述，本文先应用响应曲面法对单晶材料微磨削表面粗糙度建立预测模型，并分析磨削用量之间的交互关系，再结合BP神经网络加以优化，使预测模型更加准确，达到良好的应用效果。

1 实验条件

微尺度磨削机床选用JX-1A型精密机床；磨棒选用磨粒为500#、磨头直径为0.9 mm；检测仪器选用法国STIL公司生产的MICROMEASURE三维轮廓仪；实验材料选用镍基单晶高温合金DD98，如图1所示。

2 响应曲面法预测模型实验

响应曲面法是综合数学、统计分析原理和试验设计来研究影响因子与输出响应结果之间的一种数学模式，根据各学科试验所需，设计出符合响应曲面法的一套实验，得到预测期望的响应值和因子水平［5］。

响应曲面法由实验设计、模型拟合和过程优化三方面组成。在实验设计方面，首先应选择适合的实验方法，通过该实验获得的数据才能可靠并有效；再通过1阶或2阶函数模型的拟合，获得较好的响应曲面近似函数。从几何学角度进行分析，为了使响应输出变量Y达到最优的各影响因子组合，应进一步了解各个因子对响应输出变量Y的影响过程和影响趋势，故选用二阶响应曲面模型函数。

实验设计方法有中心复合设计和Box-Behnken设计。因为中心复合设计具有序贯性、较高的柔性、高效性等特点［6］，且在粗糙度中某一处的极值对实验来说至关重要，而Box-Behnken设计是不需要关注某些极值处响应的情形，因此本实验选用中心复合设计。

2.1 实验方案与结果分析

2.1.1 实验方案

在该实验预测中选用外切中心复合设计，即基于正交可旋转中心复合设计方案，安排20组实验，微磨削工艺参数分别为主轴转速n、磨削深度ap、进给速度fm，分别用变量x1、x2、x3表示，Zj代表编码，见表1。

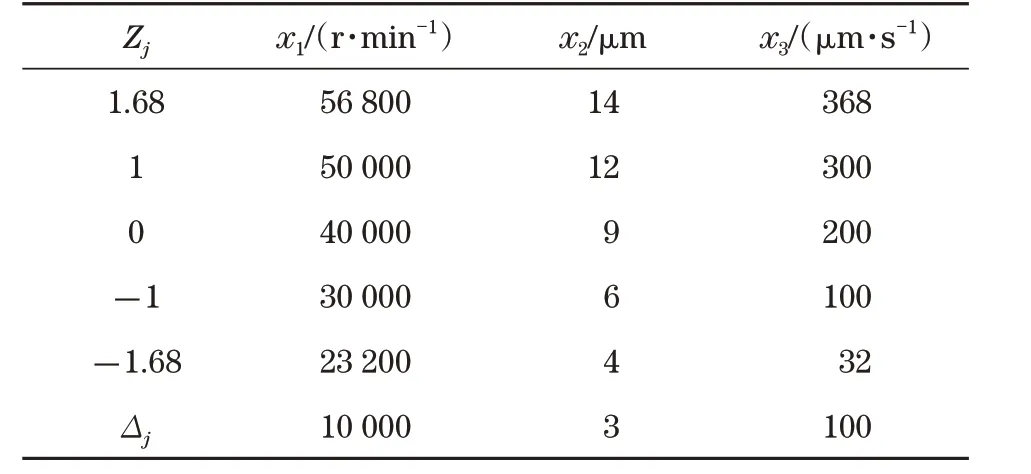
表1 因素水平编码表Tab.1 Coding of factors

2.1.2 函数模型选择

选用二阶响应曲面模型函数，用Design Expert软件对实验数据进行计算。

由于在响应曲面法中，响应值与自变量之间的函数关系未知。首先应建立起输入因子与输出响应值两者之间的函数关系，通过响应曲面法得到预测系统的响应值y，输入对应的变量。该系统有3个影响因子，分别为Z1、Z2、Z3。响应函数ε未知，代表系统误差，是一种统计意义上的误差，通常假设均值为0，那么二阶模型函数可以写成

得到的函数方程为

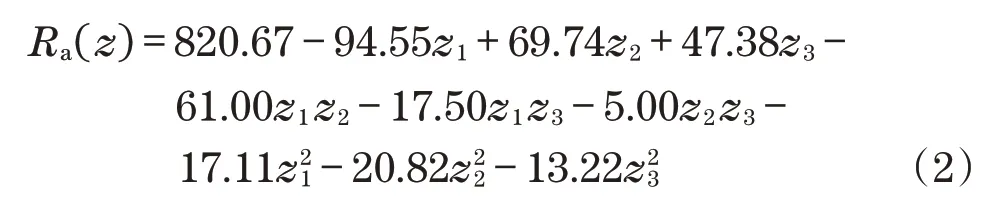
2.1.3 模型方差和F检验

对式（3）进行方差分析和回归模型F检验，可以判断方程的显著性，结果见表2。

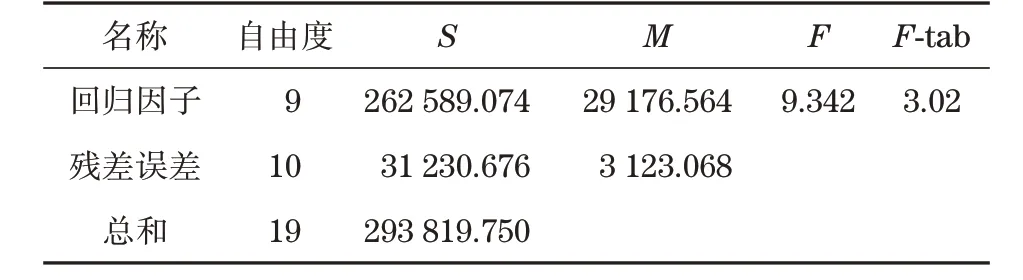
表2 回归方程显著性检验Tab.2 Significant test of regression eqution

表2中，S为平方和，M为均方差。表中所得的F值为9.342，由数查阅F分布值F-tab=F0.05（9，10）=3.02，因为9.342＞3.02，可知该预测模型显著性明显，可信度较高。

2.1.4 结果分析

将预测的表面粗糙度模型函数进行拟合，得到响应曲面和等高线图，各磨削参数对表面粗糙度的影响如下：

（1）主轴转速和磨削深度对Ra的影响。由图2可知，主轴转速和磨削深度对表面粗糙度的影响。当进给速度为零水平（fm=200 μm/s）时，从响应曲面图2（b）可以看出［7］，随着主轴转速的提高，表面粗糙度值减小；随着磨削深度的减小，表面粗糙度值也减小。从等高线曲线图2（a）可知，主轴转速和磨削深度对表面粗糙度影响的趋势，其中Ra的等值线沿着磨削深度方向的坐标轴的密集程度大于沿着主轴转速方向的坐标轴的密集程度，这种密集程度代表Ra随着该轴所代表的因素的变化率，因此主轴转速对表面粗糙度的影响较大。从曲面图也可观察出主轴转速与磨削深度的交互关系，4个顶点的数值分别为540、790、730、960 nm，当主轴转速由50000 r/min降低到30000 r/min，且磨削深度为6 μm时，其表面粗糙度值增大了250 nm，磨削深度为12 μm时，表面粗糙度值增大了230 nm；当磨削深度由6 μm增加到12 μm，且主轴转速为30000 r/min时，其表面粗糙度值由增大了170 nm，主轴转速为50000 r/min时，表面粗糙度值增大了190 nm。从彼此之间增加的数值可以看出，主轴转速与磨削深度之间的交互作用不是很强，说明主轴转速与磨削深度在影响磨削表面粗糙度方面只有轻微的影响关系。并且当主轴转速接近50000 r/min，磨削深度接近6 μm时，其表面粗糙度较好。

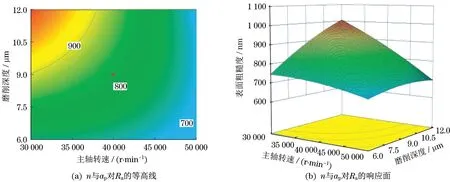
图2 n与ap对Ra的等高线、响应面Fig.2 Contour，response surface of n and ap to Ra

（2）主轴转速和进给速度对Ra的影响。图3为磨削深度取零水平（ap=9 μm）时的响应曲面图和等高线图。从响应曲面图3（b）可知，表面粗糙度值随主轴转速的提高、进给速度的降低而减小。在等高线图3（a）中可知，进给速度对表面粗糙度的影响大于主轴转速的影响。从曲面图也可观察出主轴转速与进给速度的交互关系，4个顶点的数值分别为680、710、770、1000 nm，当 主 轴 转 速 由30000 r/min提高到50000 r/min，且进给速度为100 μm/s时，其表面粗糙度值增大了60 nm，进给速度为300 μm/s时，表面粗糙度值增大320 nm了；当进给速度由100 μm/s增加到300 μm/s，且主轴转速为30000 r/min时，其表面粗糙度值增大了230 nm，主轴转速为50000 r/min时，表面粗糙度值增大了30 nm。从彼此之间增加的数值可以看出，主轴转速与进给速度之间的交互作用很强，说明主轴转速与进给速度在影响磨削表面粗糙度方面有较强的相互影响关系。当主轴转速接近50000 r/min，进给速度接近100 μm/s时，可以取得较好的表面粗糙度。

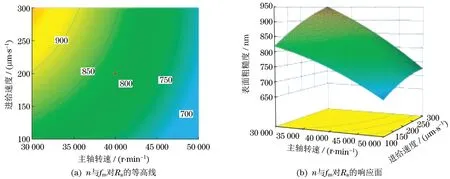
图3 n与fm对Ra的等高线、响应面Fig.3 Contour，response surface of n and fm to Ra

（3）磨削深度和进给速度对Ra的影响。如图4所示，表示的为主轴转速取零水平（n=40000 r/min）时的响应曲面图和等高线图。从响应曲面图4（b）中可以看出，随着磨削深度的减小和进给速度的降低，表面粗糙度值也随之减小，即被加工表面形貌更好。从等高线图4（a）中可知，进给速度对表面粗糙度的影响大于磨削深度的影响。从曲面图也可观察出磨削深度与进给速度的交互关系，4个顶点的数值分别为670、780、800、900，当磨削深度由6 μm增大到12 μm，且进给速度为100 μm/s时，其表面粗糙度值增大了120 nm，进给速度为300 μm/s时，表面粗糙度值增大了130 nm；当进给速度由100 μm/s增加到300 μm/s，且磨削深度为6 μm时，其表面粗糙度值由增大了110 nm，磨削深度为12 μm时，表面粗糙度值增大了100 nm。从彼此之间增加的数值可知，磨削深度与进给速度之间的交互作用不是很强，说明磨削深度与进给速度在影响磨削表面粗糙度方面只有轻微的相互影响关系。当磨削深度接近6 μm时，进给速度接近100 μm时，可获得较好的表面粗糙度。

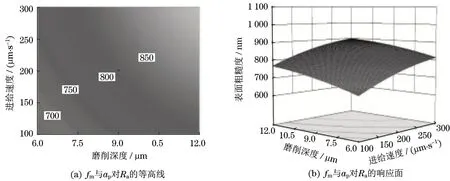
图4 fm与ap对Ra的等高线、响应面Fig.4 Contour，response surface of fm and ap to Ra

为了更加精确地预测主轴转速、磨削深度和进给速度对DD98表面粗糙度的影响，同时使所获得的预测模型更具有优化性，需对响应曲面法得到的预测模型进一步优化，采用BP神经网络算法对其进行优化。

3 BP神经网络优化预测模型实验

3.1 优化方案

只考虑主轴转速、磨削深度和进给速度3个因素对表面粗糙度的影响，因此输入层节点为3个，输出层节点数为1。该模型的拓扑结构为［3-11-1］，隐层的传递函数选用双曲正切S型函数（tansig），输出层选用线性传递函数（purelin）。

3.2 训练样本数据

设计16组三因素四水平的正交实验方案，将其前14组数据做为建模所用，以获得做为BP神经网络数据中的目标值，第15、16组通过响应曲面预测模型获得，见表3。

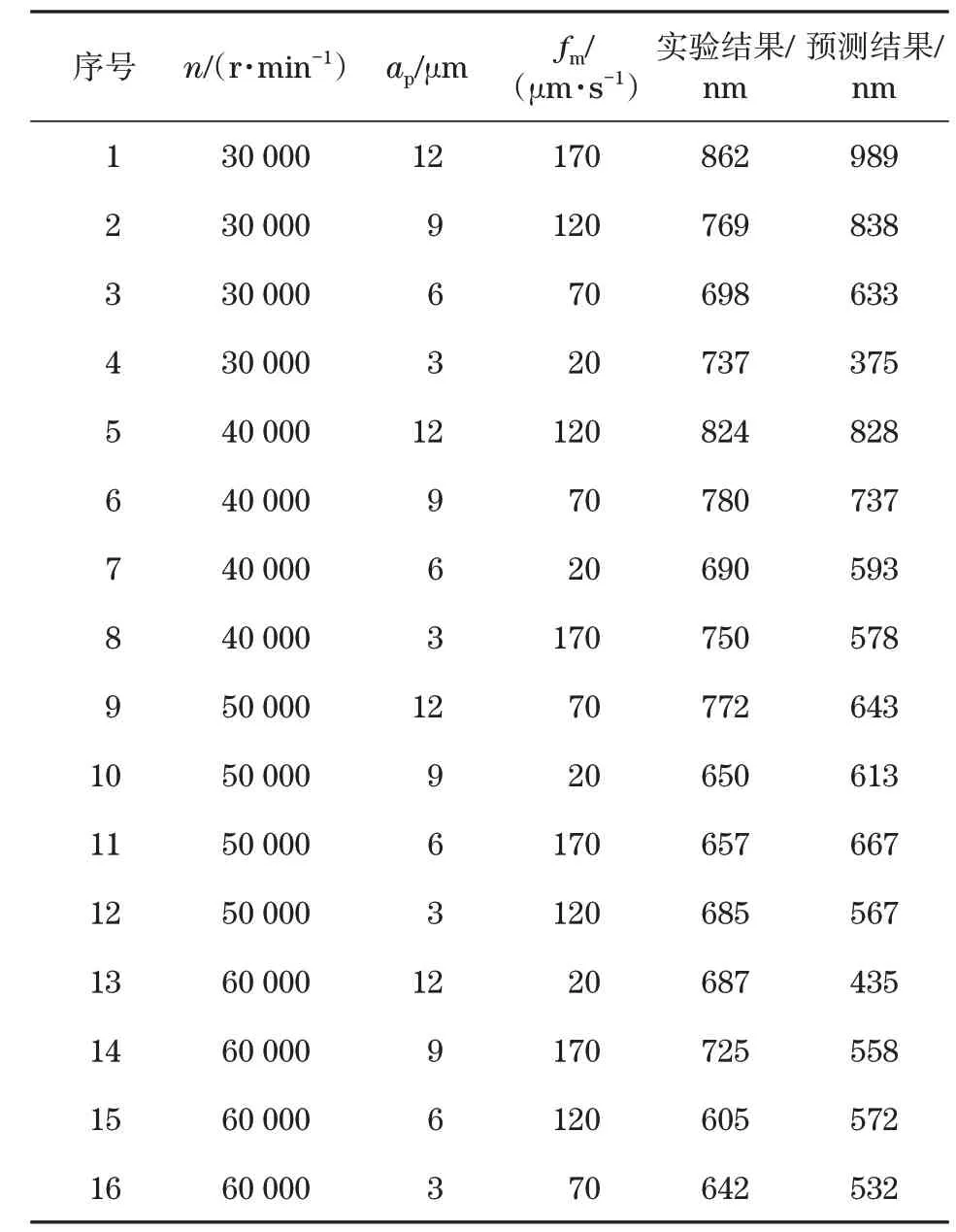
表3 正交实验实验值与预测值Tab.3 The experimental value and predictive value of orthogonal experiment

本网络选用trainlm算法为训练函数［8］，并确定学习率为0.007，最大训练次数1000，均方误差0.001，训练最长时间为1000 s。

3.3 预测结果分步

图5为BP神经网络进一步对响应曲面法得到的回归方程进行优化的情况。由于要求训练精度为0.001，由图5（a）可以看出当训练达到47步时，其精度已经达到要求训练精度。如图5（b），实验中得到的实际表面粗糙度值与预测模型拟合之后的数据进行对比，可见两者数据的拟合曲线几乎处于重合状态。由图5（c）误差曲线图可说明模型的优越性，最大相对误差为0.62%，相对误差精度处于很小的状态，与实际情况符合程度很大。

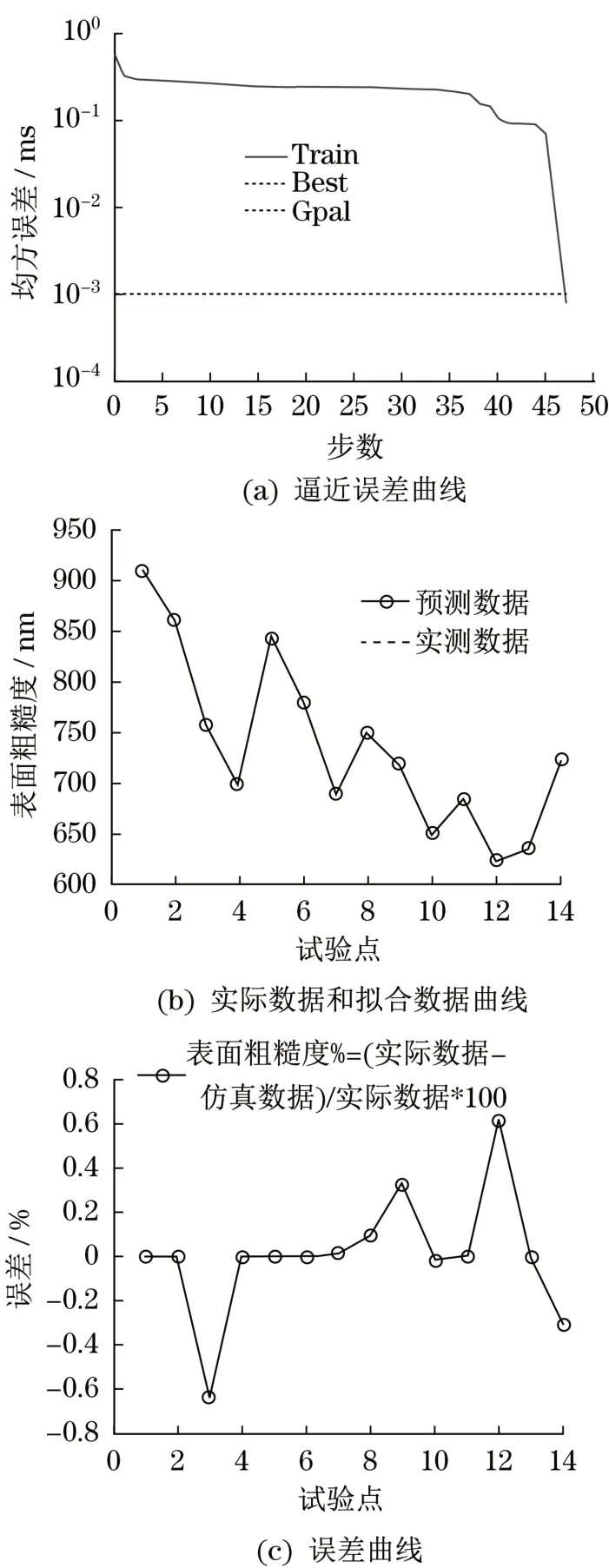
图5 BP神经网络优化结果Fig.5 The optimization results of BP neural network

3.4 模型对比验证

为了验证优化模型的准确性和实际应用性，在磨削用量预测范围内通过实验得到实验值，结合响应曲面法预测模型公式和BP神经网络优化模型分别得到相对误差值，验证结果见表4。

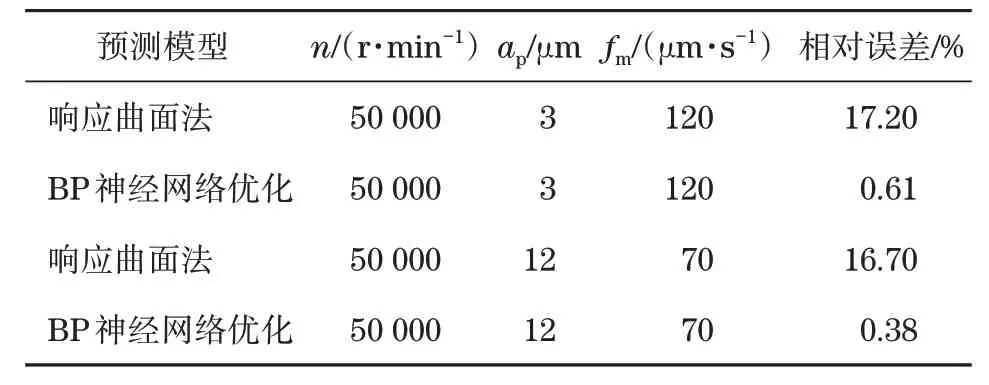
表4 预测模型相对误差对比Tab.4 Relative error comparison of predictive model

由表4可知，在磨削参数相同的情况下，应用响应曲面法得到的相对误差大小分别为17.2%和16.7%，而BP神经网络优化后得到的相对误差大小分别为0.61%和0.38%。通过对比发现，应用BP神经网络优化后的预测值明显接近实验真实值。因此，由实验证实此优化模型可以作为预测单晶DD98在受主轴转速（n）、磨削深度（ap）和进给速度（fm）3个因素对磨削表面粗糙度影响的模型。

4 结语

通过响应曲面法实验，初步建立镍基单晶高温合金DD98微尺度磨削表面粗糙度预测模型，同时得到磨削用量对表面粗糙度的影响规律，表面粗糙度随主轴转速的提高、磨削深度的减小和进给速度的降低而减小。在磨削用量对表面粗糙度影响的交互关系中，得到主轴转速与进给速度在影响表面粗糙度方面有较强的相互作用关系，而主轴转速与磨削深度、磨削深度与进给速度在影响表面粗糙度方面只有轻微的相互关系。应用BP神经网络对响应曲面法获得的预测模型进一步优化，通过验证实验对比响应曲面法预测模型与优化模型所得的相对误差大小，得到该优化模型的相对误差值接近0.61%和0.38%，在表面质量为微米级的精度上，其预测值与真实值几乎接近。因此，此优化模型具有更好的实际应用性。