基于Matlab与CoppeliaSim联合仿真的高空作业车机械臂路径规划研究
杨铁滨,茅烁,王海滨,于宗辰,张育铭
(东北林业大学工程技术学院,黑龙江 哈尔滨 150040)
随着人们对城市绿化的重视,以及避免道路两侧枯腐树枝断裂掉落而导致安全事故发生,需要大量使用高空作业车来对高处树枝树干进行修剪工作。现在高空修枝的作业方式都是工作人员站在高空作业车平台上进行操作,工作过程中地存在安全隐患,工作效率低。在我国,每年都会因为产品设计本身存在的问题或机械操作的不规范造成一些安全事故。所以,要从根本上减少或杜绝人员伤亡事故,提高修枝工作效率,避免城市交通阻塞,就要用机械代替人力进行操作,从而实现高安全性、高效率的高空作业[1]。
路径规划一直是空间机械臂的重点研究方向之一,它旨在机械臂工作空间中找到一条从初始点到目标点且不与障碍物发生碰撞的最短路径[2]。目前,国内外学者对路径规划问题已获得了一些研究成果。路径规划方法大致可以分为2种:①是传统的路径规划方法,如人工势场法、A*算法、RRT算法等[3];②是与智能算法相结合的路径规划方法,如遗传算法、蚁群算法(ant clony optimization,ACO)、基于视觉的智能算法等[4]。在上述算法中,ACO具有很强的局部寻优能力,本文选择ACO对机械臂进行路径进行规划研究[5]。
CoppeliaSim能够方便地实现多刚体系统的运动学及动力学仿真,Matlab具有强大的计算功能,并可以方便地构建控制系统[6]。利用这2个软件建立机械臂的联合仿真系统,既可以对机械臂的运动学及动力学进行仿真分析,又可以搭建机械臂的控制系统,通过交互式联合仿真,可以有效地提高机械臂的性能,为实际物理样机的研制提供技术依据[7]。
1 基于ACO的三维路径规划算法
三维路径规划指在已知三维地图中,规划出一条从出发点到目标点满足某项指标最优,并且避开了所有三维障碍物的三维最优路径[8]。一般三维路径规划算法存在计算过程复杂、信息存储量大、难以直接进行全局规划等问题。ACO具有分布计算、群体智能等特点,在路径规划算法中有较大优势。
1.1 算法流程与Matlab程序
基于ACO的三维路径规划算法流程如图1所示。基于ACO的三维路径规划算法主要包含4个函数:①启发值函数,该函数主要用于计算可视区域内各点的启发值;②适应度计算函数,该函数主要用于计算每条路径上的适应度值;③路径搜索函数,该函数采用ACO根据信息素和启发值,搜索出从出发点到终点的三维路径;④主函数,该函数主要用于ACO的全局寻优,通过迭代寻找全局最优解。
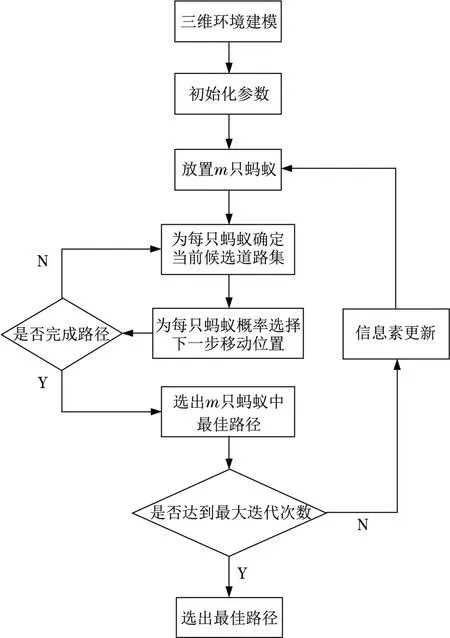
图1 三维路径规划算法Fig.1 Three dimensional path planning algorithm
1.2 仿真结果
采用ACO进行三维路径规划,为展示算法的精度,便于宏观判断,规划范围为200 m×200 m×200 m的城市街区,其中X、Y、Z轴方向每个节点的间距为50 m。路径起点在规划空间的序号为[11050],终点在规划空间的序号为[214150]。算法的基本设置为种群规模为100只,算法迭代200次,路径规划结果如图2所示。
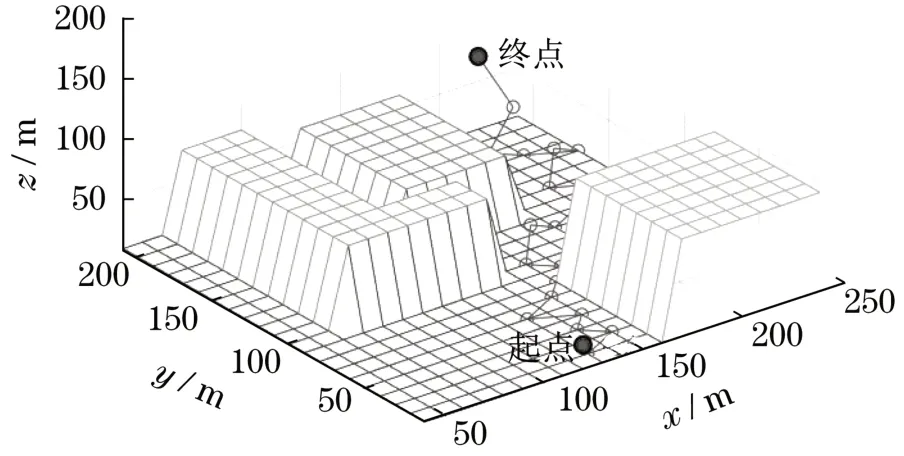
图2 仿真结果Fig.2 Path planning results
2 虚拟样机机械系统
2.1 机械臂三维模型的建立
CoppeliaSim具有很强的机械臂运动学仿真能力,但很难精确建立复杂的三维实体模型[9]。因此,利用SolidWorks建立了高空修枝工作装置的实体模型。设计的机械臂具有4个关节,能实现4自由度的回转运动。机械臂三维模型如图3所示。
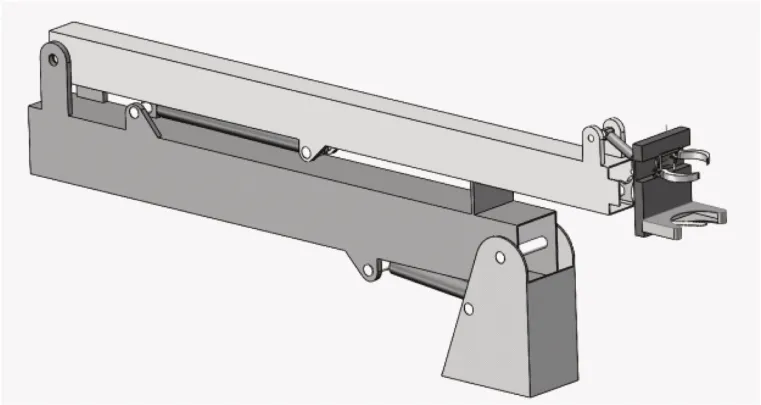
图3 机械臂三维模型Fig.3 Three dimensional model of manipulator
2.2 机械臂运动仿真系统的建立
机械臂运动学仿真需要在CoppeliaSim中进行,因此需要将SolidWorks中建立的三维模型导入到CoppeliaSim中。其方法是将SolidWorks中的文件保存为STL格式,然后导入到CoppeliaSim中[10]。在CoppeliaSim中,对导入的每个零部件进行编辑,定义其材料、质量、转动惯量等相关属性,从而使虚拟样机与实际物理样机具有相同或者相近的物理特性,以便更好地模拟实际系统。然后对机械臂添加转动副约束,定义约束后的机械臂模型如图4所示。

图4 定义约束后的机械臂模型Fig.4 Manipulator model after defining constraints
3 联合仿真系统
联合仿真的核心是输入变量与输出变量数据的实时交换。使用CoppeliaSim的逆运动学求解器(IK)模块,可以根据机械臂末端执行器的位置,自动逆向求解出机械臂各关节的绝对位置和绝对角度,进行机械臂在笛卡尔空间的运动控制。在Matlab中利用Simulink仿真模块搭建联合仿真控制系统,将ACO三维路径规划输出的路径点和机械臂的初始点作为输入变量,机械臂的绝对位置和各关节的绝对角度作为输出变量,进行机械臂的控制,从而实现机械系统与控制系统的联合仿真。
3.1 CoppeliaSim模型
在CoppeliaSim中进行联合仿真时输入变量的设置,如图5所示。
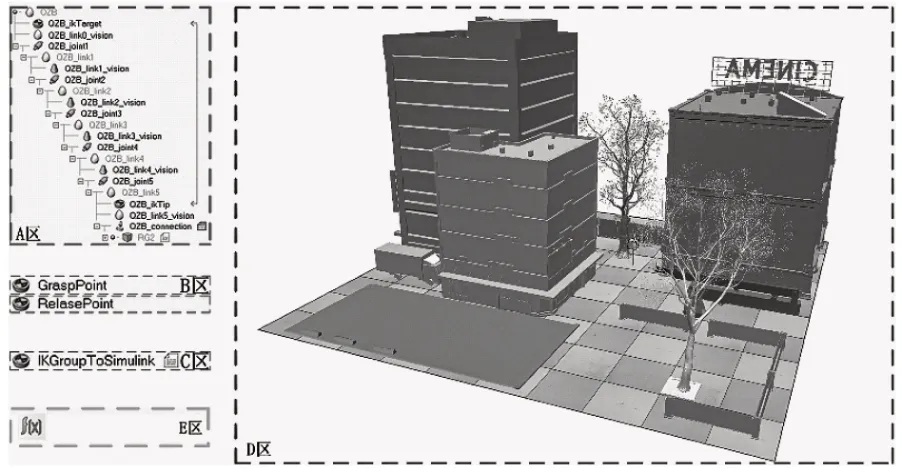
图5 仿真场景模型Fig.5 Simulation scene model
图中,如A区所示,在CoppeliaSim中建立机械臂连接关系模型树;如B区所示,在CoppeliaSim中通过使用dummy点来进行笛卡尔空间的辅助定位,进而在控制机械臂时确定修枝和放置枝桠时的绝对位置;如C区所示,通过设置IK Group To Simulink,获取CoppeliaSim自带的逆运动学计算工具,方便在Simulink中进行控制;如D区所示,在CoppeliaSim中搭建仿真所需的街道环境,使仿真更接近于真实场景;如E区所示,设置CoppeliaSim中的IK计算模块,使其应用于所需机械臂的计算,并依次设置机械臂的每个关节,通过Simulink控制机械臂的关节位置。
3.2 Simulink模型
在Simulink中搭建联合仿真时的接口、输入、输出及控制模块,如图6所示。
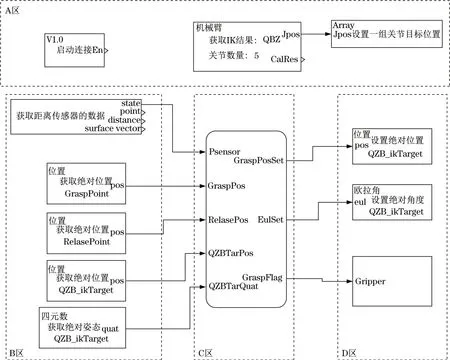
图6 Simulink模型Fig.6 Simulink model
图中,A区为Simulink与CoppeliaSim联合仿真的接口模块;B区为输入变量,获取机械臂运动过程中末端执行器的绝对位置和绝对姿态;D区为输出变量,输出机械臂运动所需的绝对位置和绝对角度;C区为Stateflow模块,通过编写的流程动态,实现联合仿真时从输入变量到输出变量的转变。
3.3 联合仿真控制系统
联合仿真控制系统主要通过Simulink模型中的Stateflow模块实现。通过编写的流程动态代码,实现联合仿真时从输入变量到输出变量的转变。流程动态如图7所示。
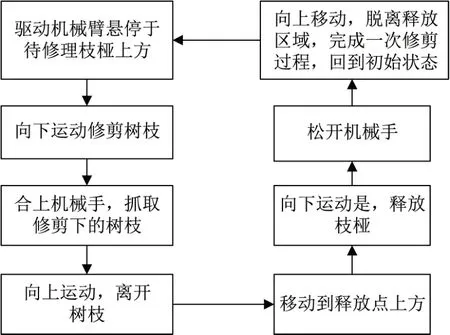
图7 Stateflow流程动态Fig.7 Stateflow process dynamic diagram
4 仿真结果讨论
为了对机械臂联合仿真系统的性能进行验证,以末端执行器为例,分别测试了末端执行器运动到待修剪枝桠处X、Y、Z坐标位置变化,如图8~图10所示。
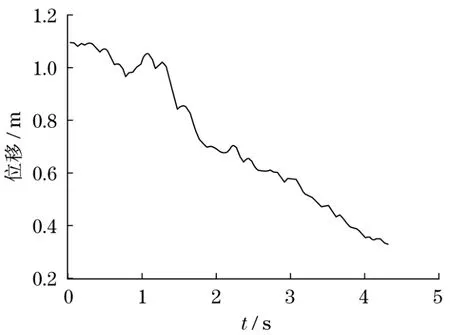
图8 末端执行器在X方向上的坐标位置Fig.8 Coordinate position of end effector in X direction
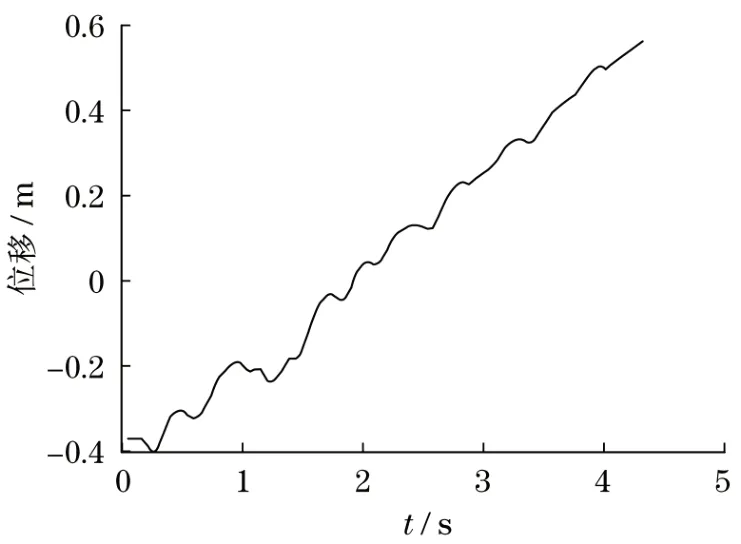
图9 末端执行器在Y方向上的坐标位置Fig.9 Coordinate position of end effector in Y direction
通过联合仿真分析可知,末端执行器在较短的时间内,可以由初始位置上升,并稳定地达到目标位置。CoppeliaSim的仿真过程证明,机械臂末端执行器由初始位置迅速到达指令给定位置,并在该位置保持不变,具有较好的轨迹跟踪性能。
在末端执行器X、Y、Z坐标位置变化曲线中,仿真实验在刚开始时,会有较大的波动,其主要原因是现有机械臂控制系统受自身重力影响起动惰性较大,但幅度对路径规划影响不大,系统很快达到收敛。
5 结语
本文开发的虚拟仿真设计方法,在避免推导繁琐的运动学方程的情况下,实现高空作业车机械臂的路径规划仿真设计,降低了机械臂开发成本的同时,节省了迭代设计时间。通过应用Solidworks、Matlab、CoppeliaSim建立了高空作业车机械臂模型,并通过基于ACO的三维路径规划算法计算出机械臂末端执行器运动轨迹,建立了联合仿真控制系统。通过仿真实验验证了机械臂系统的可行性。所采用的设计分析方法,为机械臂路径规划研究提供了一种新的途径。本文提出的虚拟设计和仿真技术还可以为高空作业车操作员提供操作和培训指导,在降低操作难度的同时,更能大大提高生产作业效率。

