基于ESO的起重机刚架结构离散拓扑优化研究
张氢,颜廷鹏,霍佳雨,孙远韬,秦仙蓉
(同济大学机械与能源工程学院,上海 201804)
随着超巴拿马型集装箱运输船舶的发展,集装箱运输船舶的宽度急剧增加,3E+型超大型岸边集装箱起重机(岸桥)也被开发出来。新型岸桥朝着超大型、高速和智能化方向发展,对金属结构的轻量化提出了迫切要求。金属结构作为岸桥的主要承力部件,其合理布局方式是首要关键。岸桥的开发阶段传统上采用类比法设计,依赖于工程师的工程经验,新机型的总体设计方案很多是直接沿用现有机型,在总体布局上还缺乏创新。
离散体结构拓扑优化的研究对象主要是刚架、桁架结构,对于岸桥、起重机等的金属结构优化有着较好的应用前景。陶义等[1]基于仿生设计的思想,以塔式起重机臂架为优化对象,以王莲叶脉为仿生原型对象,基于模糊相似理论对比了塔式起重机臂架同王莲叶脉的相似度,分析总结了王莲叶脉生长的拓扑构型规律,提出了一种新型的塔式起重机臂架设计方案,改变臂架腹杆的布置方式,减少了臂架腹杆的数量,同时减少了制造过程中的焊接次数。焦洪宇等[2]针对塔式起重机臂架采用连续体拓扑优化和骨架提取的桁架结构优化设计方法进行腹杆布局优化。刘炜等[3]采用ANSYS软件集成的变密度法连续体拓扑优化技术对岸桥门框斜撑进行优化设计,以抗风振要求作为主要设计条件,得到了3种斜撑的布置方案。李旲等[4]结合模糊推理和神经网络,根据已有桁架结构的构成机理,对桁架拓扑结构进行抽象化数字提取,并依此推导出新的桁架结构基结构形式,以桁架结构重量为优化目标函数,建立了桁架结构智能布局优化系统。刘红艳等[5]基于拟满应力的思想,提出了一种改进的遗传算法,对结构中的杆件编码,并应用遗传算法求解了刚架结构拓扑优化问题,在此基础上应用拟满应力算法实现截面尺寸优化,改进算法搜索方向更加明确,计算速度更快。
在岸桥结构中,采用离散体拓扑优化技术进行门框斜撑布局的研究较少。本文首先基于渐进结构优化思想[6],以结构应变能为优化目标,将传统连续体单元的自变量的连续变化,离散化为给定设计域内基结构的杆件的增删,研究对于基结构进行离散单元退化操作(单向删减)实现给定刚架结构拓扑优化的算法;然后应用离散单元退化策略(单向删减)实现给定参数岸桥的门框基结构斜撑拓扑优化,实现斜撑的合理布局。
1 基于ESO的拓扑优化数学模型
将基于渐进结构优化(ESO)算法的离散体拓扑优化应用到岸桥中,考虑优化目标函数与变量灵敏度的定义。采用结构刚度为优化目标函数可以满足岸桥使用过程中的变形不超过设定值,在大跨度岸桥结构优化应用中是主要控制指标。ESO拓扑优化过程中的设计量删减与单元灵敏度有关,本文应用差分法定义离散变量的灵敏度。
1.1 体积约束下的结构刚度优化模型
岸桥工作时,按照金属结构设计规范,不希望发生较大变形。刚度表征是结构抵抗外力变形的能力。工程中结构优化设计经常选择结构的刚度作为优化目标函数。结构的应变能是外力作用在结构上所做的功,结构的应变能和结构的刚度呈倒数关系。结构的应变能越小,结构在外力作用下的变形越小,结构的刚度越强。针对结构刚度拓扑优化问题,以保留结构体积为约束条件,结构的刚度最大,即结构的应变能最小为目标函数,提出了刚度拓扑优化问题的数学模型:

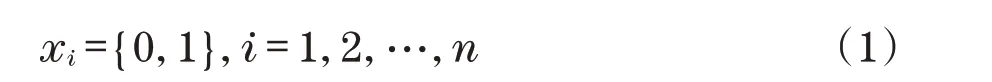
式中:{P}为作用在结构上的载荷列阵向量;{U}为节点的位移列阵向量;c({x})为结构的整体应变能;Vi为第i个单元的体积;V0为结构的初始体积;β为结构约束的体积分数;xi为第i个单元设计变量的取值,xi=0为第i个单元删除,xi=1为第i个单元保留。
1.2 离散单元灵敏度的计算
离散拓扑优化无法做到像连续体那样通过对设计变量求导单元对结构刚度的灵敏度值,但可以利用差分法求得,整体应变能如下:

在有限元分析中,结构的静态特性如下:

保证载荷向量列阵不变,对结构单元进行增删操作:
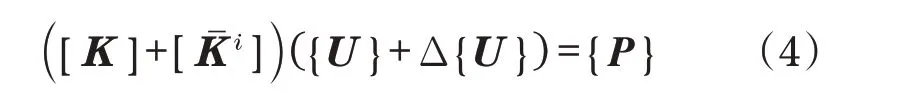
式中:[]为对第i号单元扩维了的刚度矩阵;Δ{U}为整体结构位移列阵的变化量。
将式(4)减去式(3)并略去高阶无穷小量,得

将式(5)代入式(2)得
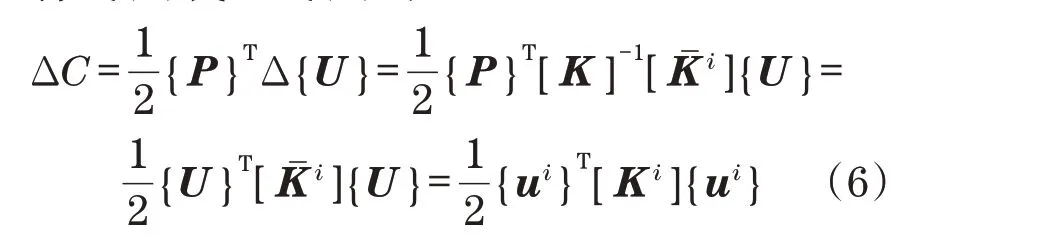
式中:[Ki]为第i号单元的刚度矩阵;{ui}为第i号单元的位移向量。
第i号单元对于应变能的灵敏度为
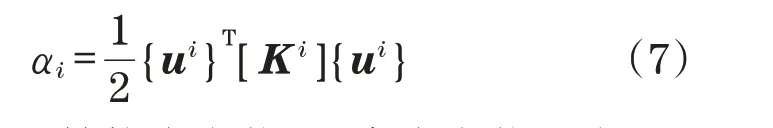
目标函数是结构应变能,要求应变能要小,所以在进行单元增删操作时,单元对于结构刚度变化的灵敏度成为考量的重要指标。
2 应用于岸桥的离散体拓扑优化策略
2.1 基于ESO离散体拓扑优化
给定的设计域基结构如图1所示,有如下参数:初始节点、成长节点、进化杆件、待进化杆件、退化杆件、待退化杆件。
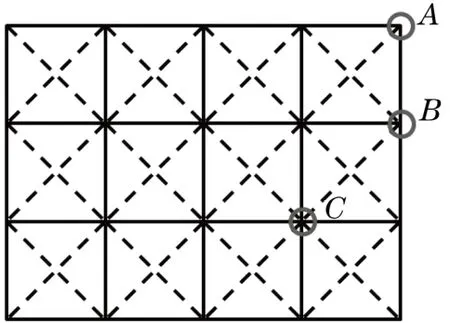
图1 节点类型Fig.1 Schematic diagram of node type
结构中的节点按照所处位置的不同,可分为角节点、边节点和自由节点。图1中:A节点为角节点,只有一个待进化杆件与之相连;B节点为边节点,有3个待进化杆件与之相连;C节点为自由节点,有8个待进化杆件与之相连。节点在结构中所处的位置的不同,当该节点被选中成为成长节点时,同节点相连的待进化杆件数目也不同,待进化的杆件的数目越多,当前迭代步中,结构进化方向的可能性就越多,当前迭代步的搜索能力越强。结构中的成长节点数量会随着优化迭代增多,这表明搜索能力随着优化过程不断增强。
2.2 基于退化策略的离散体拓扑优化
结构中存在的杆件过多,势必会存在对结构刚度贡献较小的杆件,造成材料的浪费。从结构中不断删除刚度贡献较小的杆件,保留对结构刚度贡献较大的杆件,可以节省材料,减轻结构的重量,充分发挥材料的力学性能。
虽然向结构中增添斜撑,可以有效提升结构的刚度,但是结构中的斜撑并不是越多越好,部分斜撑对于结构刚度贡献较小,将这些杆件删除后,结构的应变能增删幅度很小,即认为这些杆件在结构中的作用较小。每次优化迭代时,选择杆件中单元灵敏度最小的杆件作为结构中待退化的杆件,将这些杆件从结构中删除,结构的应变能增长幅度最小。重复上述筛选和删除杆件的操作,直到结构中待退化的杆件对结构刚度贡献较大,这部分杆件在结构中起到重要作用,不再从结构中删除杆件,优化达到收敛。
基于退化策略实现离散体的杆系结构拓扑优化,拓扑优化流程如图2所示,基本步骤如下:
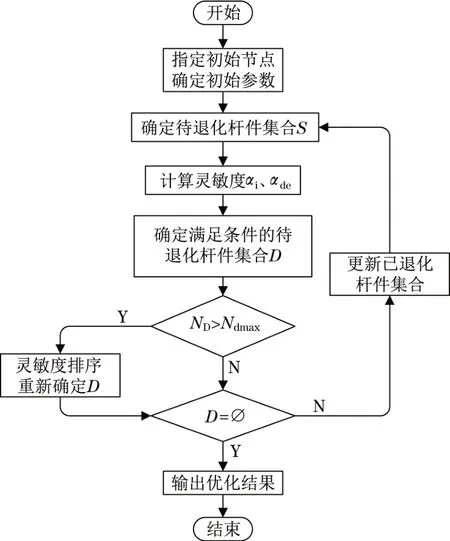
图2 基于退化策略的拓扑优化流程Fig.2 Topology optimization flow chart based on degradation strategy
步骤1确定杆系结构的初始结构、基结构,给定退化基准率βd、单次优化最大退化单元数Ndmax。
步骤2根据已退化杆件集合,更新待退化杆件的集合S。
步骤3进行结构有限元分析,并计算单元的灵敏度αi。
步骤4计算退化杆件的单元灵敏度标准为

式中:αde为退化杆件的单元灵敏度标准;αave为已退化杆件的单元灵敏度平均值。
步骤5确定当前迭代步中满足退化要求的待退化杆件集合D。
步骤6判断D中的单元数量ND是否大于Ndmax。如果是,根据单元灵敏度的大小对待退化杆件进行排序,重新确定待退化杆件集合D,转入步骤7;如果否,直接转入步骤7。
步骤7判断是否满足迭代终止要求,即D为空,结构中不存在满足退化条件的杆件。如果是,优化过程终止,输出结果;如果否,更新已进化杆件集合,并转入步骤2,继续优化。
3 离散体拓扑优化策略在岸桥中的应用
本例采取的岸桥模型尺寸为前伸距76.0 m,后伸距32.0 m,轨距30.0 m,基距20.6 m,额定起质量61 t,吊具质量19 t,小车质量30 t,起升/下降速度为满载150 m/min,空载75 m/min,小车额定运行速度300 m/min。计算岸桥工况时按竖向荷载与横向荷载施加于不同位置来确定不同工况。岸桥门框属于门式刚架结构,无支撑的岸桥门框水平刚度较弱,在岸桥门框间布置杆件,可以加强结构的刚度,门框基结构如图4所示,其中会存在大量的冗余杆件,导致材料的浪费。基于退化策略的拓扑优化方法能够保留结构中贡献较大的杆件,得到比较简洁的斜撑杆布置方案,易于在实际工程上实现,故采用基于退化策略的拓扑优化方法对岸桥模型进行拓扑优化。各构件单元类型见表1。

表1 各构件单元类型Tab.1 Element type of each component
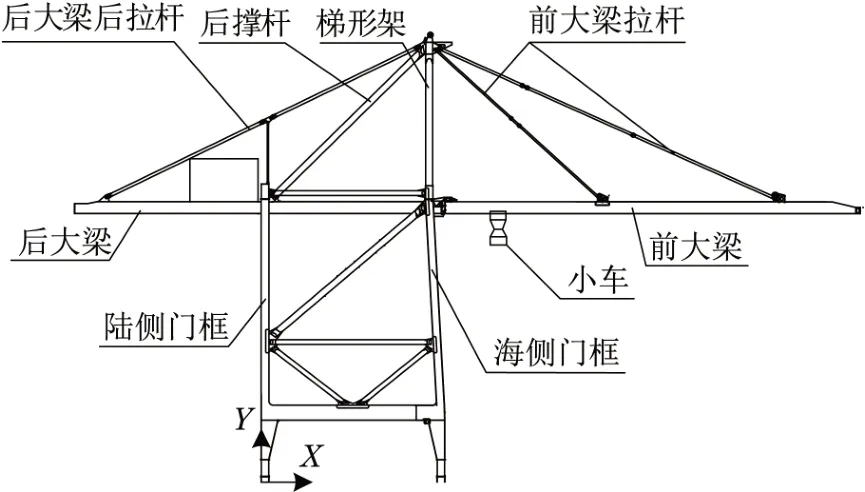
图3 岸桥结构Fig.3 Structural diagram of container crane

图4 岸桥模型的基结构Fig.4 Ground structure of container crane
岸桥门框中所有杆件之间及所有杆件与同侧立柱、陆侧立柱之间的节点均为刚性连接,初始结构中所有杆件的截面均为圆环形,外径D1=0.52 m,内径d1=0.50 m,材料弹性模量E=2.1×1011Pa,泊松比ν=0.3,岸桥工况及其参数选择见表2,岸桥模型的基结构如图4所示。

表2 岸桥工况及其参数选择Tab.2 Working conditions and parameter selection of shore bridge
对于前3种工况,应用退化策略得到的结构形式相差不大,优化结果如图5所示,显示海陆侧门框间保留的杆件形成2根比较长的对角撑杆,呈X型布置。工况4门框优化过程如图6所示,最终结构显示海陆侧门框间保留的杆件形成两根比较长的对角撑杆,呈X型布置,同时在陆侧门框立柱与海陆侧联系上横梁夹角处保留有杆件,这根杆件同陆侧门框立柱、海陆侧联系上横梁共同构成了一个三角形,能够对这个夹角起到加强作用。各优化结果见表3。
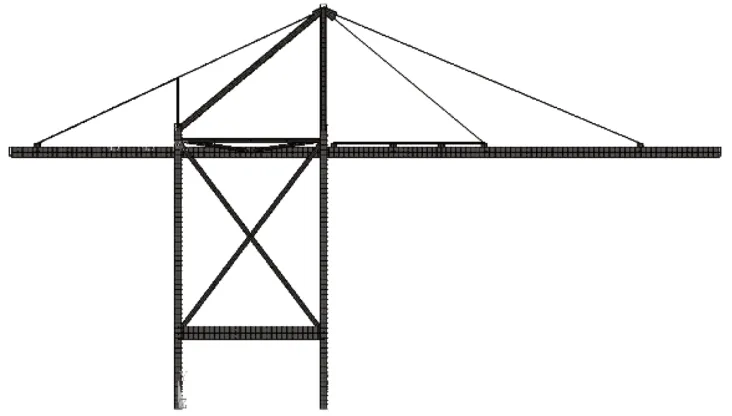
图5 工况1、2、3岸桥拓扑优化后结构Fig.5 Topology optimization structure of shore bridge under working conditions 1,2 and 3
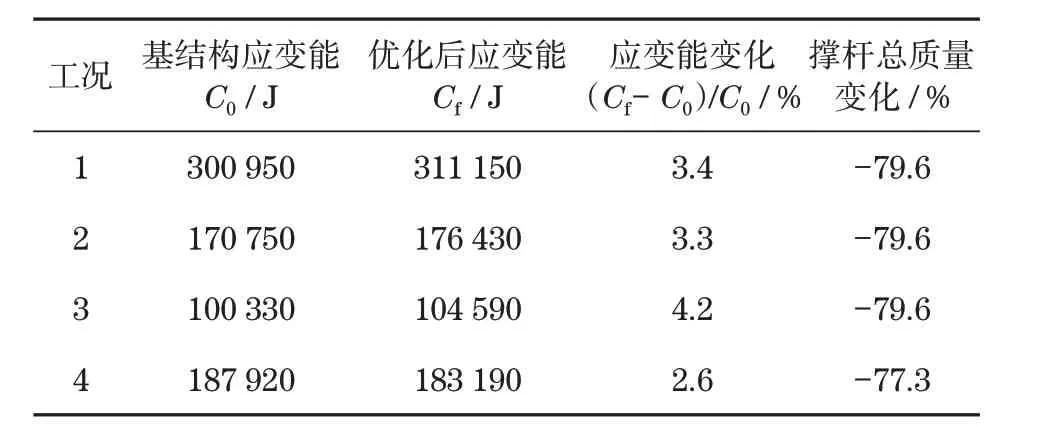
表3 各个工况优化结果Tab.3 Optimization results of each working condition
初始结构中冗余的杆件被去除,节省了大量的材料。采用基于退化策略的拓扑优化方法能够有效去除对结构刚度贡献较小的杆件,保留对结构刚度贡献较大的杆件。工况4岸桥拓扑优化过程如图6所示,4个工况结构应变能变化曲线如图7所示。

图6 工况4岸桥拓扑优化过程Fig.6 Topology optimization structure of shore bridge under working conditions 4
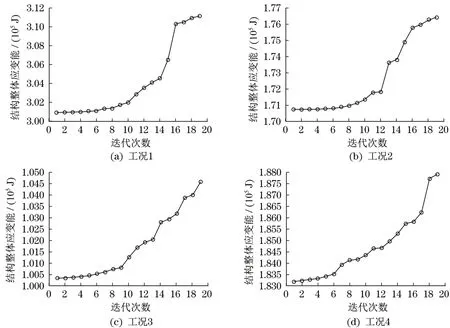
图7 结构应变能变化曲线Fig.7 Curves of structural strain energy
4 结语
基于经典的ESO拓扑优化理论,对于给定结构先预设由离散杆件构成的基结构,然后应用渐进结构优化技术中的单元退化算法,通过有限元分析逐步删减基结构中的对结构刚度贡献较小的杆件,逐步迭代,达到杆件布局较优的目的。基于退化策略的拓扑优化方法,在4种典型工况下,对岸桥模型进行拓扑优化,对结构刚度贡献较小的杆件实现逐步退化,充分发挥杆件材料的力学性能,进而实现拓扑优化的目的。结果显示,4种典型工况下岸桥模型拓扑优化结果类似,都由2根比较长的撑杆呈X型对角布置。岸桥结构的应变能有微小增加,但是优化后的结构比初始基结构的质量大大减小,达到了基于离散体拓扑优化技术实现优化的目的。

