利用风险管理指数设计定量项目室内质量控制方案的应用
张 裕,余启华,任碧琼
湖南省第二人民医院/湖南省临床检验中心,湖南长沙 410007
临床实验室质量控制(QC)理论的最新趋势强调了实验室应评估室内质量控制策略的有效性,以最大程度地减少因检测过程中的不稳定性而产生的错误结果,导致不恰当的临床决策和医疗行动对患者造成伤害的风险。美国临床和实验室标准化研究所(CLSI)已发布的指南CLSI EP23-A[1]和CLSI C24-Ed4[2]反映了这一趋势。C24-Ed4紧密结合了EP23-A中提出的风险管理的概念和原理,提出一种名为“MaxE(Nuf)”的患者风险参数,即存在未检出的失控状态时,最终报告的错误(不正确或不可接受的)患者结果数量相较在控状态下的最大增加量。在设计QC策略时,考虑将MaxE(Nuf)控制在一定数量以下[3]。需注意的是此方法只控制了报告错误结果的数量,MaxE(Nuf)仅是患者风险中伤害概率的度量[4],但这与患者风险不同,依据风险管理指南,患者风险还应取决于检验程序发生失控的频率以及报告错误的患者结果导致不恰当的医疗决策或行动而导致患者伤害的可能性[5]。为此,C24-Ed4文件制定委员会主席Parvin提出了一个新指标——风险管理指数(RMI)[6],即报告的错误结果对患者伤害的预期概率与可接受的患者伤害概率之比,来确定患者伤害风险是否得到有效控制,并开发出配套的风险防控软件,但该软件不能免费使用,现有的文献中也没有简单的工具可以计算。本研究旨在梳理RMI计算原理,通过使用常见的办公软件Excel编辑函数,利用实例计算风险管理指数水平,并绘制示意图,在一定程度上帮助实验室进行基于RMI的统计质量控制策略设计。
1 RMI的概念及原理
EP23描述了一种针对实验室质量控制的风险管理方法,该方法旨在识别实验室中所有可能的故障模式,对已识别的故障模式进行风险排序(见图1),然后制定策略预防风险发生或降低至可接受的水平。该图提供了一个模型,可用于关联实验室的检测活动如何产生患者伤害风险。首先,在实验室的测量过程中可能会出现失控的情况,失控的状况将增加产生错误患者结果的可能性。如果报告错误的患者结果,则可能对患者造成危险情况。最后,错误结果导致不恰当的临床决策和危险医学措施,从而对患者造成伤害[7]。

图1 产生患者伤害的序列事件
Parvin提出的RMI数以EP23风险模型为基础,分析产生患者伤害的一系列因素,转化为可量化的患者伤害相关参数(见图2),然后计算出存在不同程度失控系统误差时患者伤害预期概率PH(SE),以生成RMI。若患者伤害预期概率(PredictedPH)小于或等于可接受的患者伤害概率(AcceptablePH),即RMI≤1,则实验室的质量控制策略已将患者风险降低至可接受的水平。若RMI>1,则需要设计新的质控策略。PH(SE)与RMI计算公式[6]分别为:PH(SE) ={PE(0) + E(Nuf(SE))/(MPBF+ANPed(SE))}×Ph|u RMI=PredictedPH/AcceptablePHPE(0)是指检测系统处于在控状态时产生错误结果的概率。MPBF是检测系统平均失控周期内报告的患者结果数。E[Nuf(SE)]是已报告的错误患者结果数量。ANPed(SE)是从失控状态开始到被检出之间处理的患者样本平均数。E[Nuf(SE)]/[MPBF+ANPed(SE)]是指发生失控误差而导致错误患者结果概率的增加。PE(0)+E[Nuf(SE)]/[MPBF+ANPed(SE)]是指在控和失控状态期间出现错误结果的总概率。Ph|u是指报告的错误结果导致的不当医疗决策或医学措施而导致患者伤害的概率评估。PredictedPH是指不同失控误差大小时,平均患者伤害预期概率。AcceptablePH是指最大的可接受的患者伤害概率。

图2 产生患者伤害的序列事件及患者伤害预期概率相关参数
2 利用RMI设计室内质控方案的实际操作
根据上述公式以及各参数的定义,可以利用Excel编辑函数进行计算。PE(0)等于在控状态时检测结果超出质量要求范围的概率,基于检测系统的偏移(Bias)和不精密度(CV)以及允许总误差(TEa)要求来计算,见文献[8]。MPBF等于测试系统平均失控周期(天)乘以每天分析物的平均患者结果数。E[Nuf(SE)]等于发生不同大小系统误差时的E(Nuf)值,ANPed(SE) 等于发生不同大小系统误差时的ANPed值,基于检测系统的Bias和CV,使用的QC规则,QC频率或批长度以及TEa要求来计算,见文献[8]。Ph|u来源于专家观点,文献报道或临床医生意见[4,6]。Predicted PH来源于PH(SE),是指±2TEa范围内PH(SE)的定积分,即发生±2TEa范围失控误差大小时,平均患者伤害预期概率,可按定积分原理以一定系统误差大小间隔(如1.0%或0.5%)计算PH(SE)值后再求均值。AcceptablePH需分析检测项目危险严重度,利用风险可接受性矩阵和患者伤害类别概率矩阵,确定最大可接受伤害概率。计算RMI所需相关参数、英文简称、计算公式及Excel函数见表1。

表1 利用Excel计算风险管理指数所需参数及公式

续表1 利用Excel计算风险管理指数所需参数及公式
以血清葡糖糖为例,实验室的QC方案为采用2个浓度水平质控物、质控规则为13s,TEa为10.0%,Bias为0.0%,CV为2.5%,计划的QC之间患者样本的数量(批长度)E(NB)为100。每天的标本量为100,检测系统平均失控周期为30天。根据Parvin的评估,血清葡糖糖因错误结果导致不适当的医疗决策或行动而导致患者伤害的概率为50.0%,Ph|u设定为0.5;因不适当的医疗决策或行动对患者的危害严重程度为“微小”等级。根据表2风险可接受矩阵,危害严重度等级中的“微小”等级一列,最大可接受的发生概率等级为“偶尔”。然后根据表3患者伤害类别概率的矩阵,“偶尔”等级的发生概率为0.000 01~0.000 1,上限为0.000 1。据此得出最大可接受的患者伤害概率(AcceptablePH)为0.000 1。参照表1的计算公式,在第4列“/”输入上述对应的参数,在SE(%)处按一定间隔输入不同的系统误差大小(本例从-2TEa至2TEa,间隔0.5%),P1为发生误差后质控规则的误差检出概率,因单规则与多规则功效的计算公式不同,单规则P1计算公式见文献[8-9],多规则P1计算公式见文献[10],并按SE(%)间隔计算出不同系统误差大小时的P1。上述参数的取值确定后,根据表1 Excel函数公式搭配Excel自动填充功能计算得出RMI值。

表2 风险可接受性矩阵(EP23)
表3 患者伤害类别概率矩阵(ISO 14971)
按该项目当前的质控方案,其RMI值为2.31,见表4。患者风险在现有质控策略下不可控,需设计新的质控策略。新的方案二采用了更加严格的质控规则13s/22s/R4s,在该方案下的RMI值下降至1.38,但仍未达到RMI≤1的目标,因此需再次设计新的质控策略。方案三在沿用13s/22s/R4s规则的情况下,将批长度缩短至之前的一半,即50个标本做一次QC,此方案下的RMI值降至0.89,达到了预期目标,意味着实验室当前的质控策略已将患者风险降低至可接受水平。3种方案相关数据见表4和图4。

表4 基于风险管理指数的室内质量控制方案设计示例
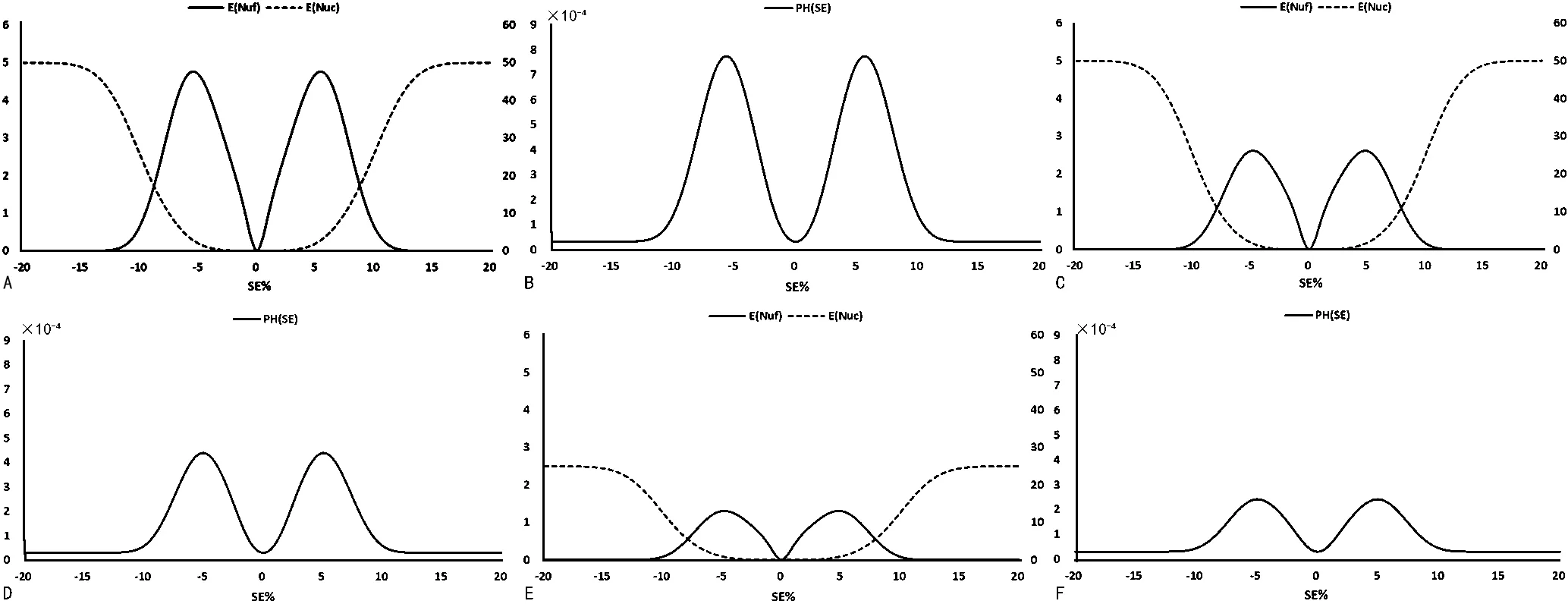
图4 不同误差状态下E(Nuf)与E(Nuc)、PH(SE)示意图注:方案一为A、B;方案二为C、D;方案三为E、F;E(Nuf)参照左侧纵坐标;E(Nuc)参照右侧纵坐标。
通过表4的数据还可以发现,检测系统处于在控状态时的患者伤害预期概率PH(0)是一个恒定的数值,在控状态时PH(SE)的计算公式为PH(0)={PE(0)+E[Nuf(0)]/[MPBF+ANPed(0)]}×Ph|u,因为没有发生系统误差而导致的错误结果数的增加,此时E(Nuf)值为0,因此PH(0)=PE(0)×Ph|u,PE(0)为检测结果超出均值±4s的概率,值为0.633 4×10-4,乘以Ph|u后即为PH(0)值。当发生很大系统误差时,实验室只需1次QC即可检出误差状态,鉴于括号式(限定区间)QC方式,产生的错误报告均可纠正,因此发出错误报告的数量为0[8],故PH(SE)曲线两边逐渐趋于平坦至PH(0)值,见图4。E(Nuf)的图形与PH(SE)的图形外观基本一致,随着质控方案越来越严格,E(Nuf)的图形波峰越来越低矮,E(Nuf)在没有发生误差时值为0,随着系统误差的增大,E(Nuf)由最初的逐渐上升,到一定数量后,也就是达到Max E(Nuf)后,开始逐渐下降,最终又接近于0,可见PH(SE)值与E(Nuf)值直接相关。E(Nuc)值随着发生系统误差的增大,由0逐渐增大,直到达到最大值E(N0)。
此外,3种方案的MaxE(Nuf)随着质控方案越来越严格,其值也越来越低。根据以往的研究[11-13],在设计基于参数MaxE(Nuf)的质控方案时,需将MaxE(Nuf)值控制在1以下,但是基于RMI的质量控制策略,MaxE(Nuf)值是否小于1并不是一个必要的条件,如方案三,尽管MaxE(Nuf)值为1.31,但该方案的RMI值为0.89,已满足风险管理要求。缘于RMI包含了产生患者伤害的全过程因素,牵涉到更多的参数,因此,亦有可能发生MaxE(Nuf)值已小于1,RMI值不一定小于1的情况。
3 小 结
CLSI C24-Ed4明确了实验室质量控制的主要目标是降低由错误检验结果导致的患者风险。实验室的质量控制策略旨在确保即使发生测试系统故障,由于报告的错误结果而导致患者伤害的风险也可以保持在可接受的水平。RMI可将实验室质控策略与患者伤害严重程度联系起来,确定患者伤害风险是否得到有效控制。但预测RMI所需的一些参数,例如检测系统平均失控周期,错误报告的结果导致不适当的医疗决策或行动的可能性,以及因不适当的决策或行动导致的患者伤害的严重性需要主观估计。这些估计值可能会有不同的意见,对其中任何一个的更改都会改变所计算出的PH(SE)和RMI值[6],因此需要权威机构来统一这些标准[4]。Excel作为常用的办公软件,不仅可以计算常用质控规则的功效,帮助实验室进行个性化室内质控设计;还可以计算E(Nuf)值,辅助设计批长度;其功能也已满足评估风险管理指数RMI的需要。随着风险管理意识的深入,实验室可利用上述方法评估RMI,完善质控策略,将患者伤害的风险降低到可接受水平。

