高填方工程工后沉降演化规律研究综述
柴玉卿,郑双飞,李 旭,杜战军,李 帅,刘 雪,丁心香
(1.河南省交通规划设计研究院股份有限公司,河南 郑州 450052;2.北京交通大学城市地下工程教育部重点实验室,北京 100044)
0 引 言
随着我国经济社会的迅速发展,国家对基础交通设施的建设愈发重视。在丘陵沟壑地区进行高速公路、机场、土石坝建设施工时,为满足建设高程和平顺性需求,经常需要采用高填方工程,该类工程主要具有以下几个特点。①填方体工程量大、施工期长[1]。在丘陵地区的高填方工程中,为满足高度需要,通常需要高填深挖,体量巨大。这不仅需要对施工时的压实度进行严格把控,也需要对分层填筑时的分层厚度进行更为细致的划分,因而造成施工期大幅度延长。对于底部填方体而言,施工期延长意味着加载时间的延长,填方体施工过程相当于分期加载,因此在分析时需考虑上部填方体自重荷载的递增[2]。②工后沉降变形控制难。施工完成时填方体最底层与顶部落差可达数十米甚至数百米,填方体自重荷载大。在自重与外部荷载作用下,不同高度处的围压及应力水平等存在巨大差异。在工后沉降逐渐完成的十余年内,荷载作用下发生的蠕变与干湿循环作用下的湿陷等不确定因素,造成工后长期沉降难以准确计算与控制[3]。③地质情况复杂。在某些地质情况复杂的丘陵地区,当存在软土地基时,高填方路段的沉降包含原软土地基的沉降以及填方体的沉降两部分[4-5]。由于上部填方体自重大造成上覆荷载大,因此需要对原软土地基进行处理,保证其承载力和稳定性[6-7]。当软土地基厚度较小时,可选择浅层换填,或者直接挖除表面软土层至稳定基岩。
综上所述,由于高填方工程的上述特点,极易出现沉降变形,对工程的安全性和服役性都造成不利影响,并且增加了后期的运营维护难度。本文针对高填方工程主要存在的工后沉降难以计算、预测和控制的问题进行调研,进而总结其工后沉降机理、变形规律、主控因素、沉降预测模型和工后沉降控制措施。
1 高填方工程工后沉降控制要求
高填方工程普遍应用于公路、机场、土石坝、地基基础、边坡等领域,不同行业中的高填方工程定义和沉降控制要求不同,存在一定的差异。对于高填方工程的定义与适用范围,在公路工程和地基基础工程中,《公路路基施工技术规范》(JTG/T 3610—2019)[8]与《高填方地基技术规范》(GB 51254—2017)[9]均将高填方工程定义为填筑高度超过20 m的工程;而在机场建设中,《民用机场高填方工程技术规范》的适用范围为填筑高度小于160 m的机场,但对于填筑高度下限并未在条文中进行明确规定。然而,该规范的制定主要针对山区新建机场,并且后附的条文说明中所列的新建机场填筑高度均超过20 m,因此实际依然将20 m作为适用该规范的下限值。在土石坝建设工程中,对高程和平顺性要求较低,因此现行的《碾压式土石坝设计规范》(SL 274—2020)[10]中将高坝定义为超过70 m的土石坝。
以上规范对高填方的定义仅考虑了填筑高度,刘创明等[11]认为在常年积水地带使用细粒土填筑的路基工程超6 m,或其他地带的路基填筑高度超18 m(土质)或20 m(石质)时,均应定义为高填方工程。该定义方法更为全面,综合考虑了地基种类,填筑材料等实际工况。
对于工后沉降控制要求,在公路工程中,现行规范《公路路基设计规范》(JTGD 30—2015)[12]中对不同路段的15年容许工后沉降要求在100~500 mm之间(表1);在机场建设工程中,现行规范《民用机场岩土工程设计规范》(MH/T 5027—2013)[13]中对机场设计使用年限内的工后沉降和差异沉降略大,在200~400 mm之间(表2);在土石坝建设工程中,土石坝工后沉降的要求与坝体高度成正比,即坝体高度越大,允许的工后沉降越大。根据《碾压式土石坝设计规范》(SL 274—2020)[10],为防止沉降过大,坝顶需预留沉降超高,其中土质防渗坝体超高值为坝体设计高度的1%。 对于100 m高的土石坝,工后沉降容许值为1 000 mm,由此可以看出公路高填方工程的工后沉降控制要求最高,土石坝最低。

表1 公路高填方路基15年容许工后沉降要求Table 1 15 years allowable post-constructionsettlement requirements 单位:mm

表2 机场填方工程工后沉降与差异沉降控制要求Table 2 Post-construction settlement anddifferential settlement
另外,现行规范应用时还有一些不确定的问题,如在公路高填方工程相关现行规范中,虽然规定了工后限定时间内的具体沉降值,但由于无法对工程进行长期持续监测,需应用工后沉降公式来预测最终沉降值,但规范并未给出计算公式;此外,规范未给出工后沉降达到最终值的稳定标准,如15~20年内工后沉降未必达到最终值,填方体依然可能会继续发生较大的沉降,因此工后沉降的预测尤为重要。
2 高填方工程工后沉降案例分析
表3为对高填方工程案例的总结,包括高填方路基、机场、堆石坝等领域,涉及的土体类型包括软土及粗粒土填料。不同工程的填土类型、填方体高度、填方体上部荷载、工后沉降控制措施不同,造成其工后沉降最终值与沉降速率有很大差异[14]。另外,施工过程中的施工速率、填料压实度以及防排水措施等都会对工后沉降造成影响[15]。
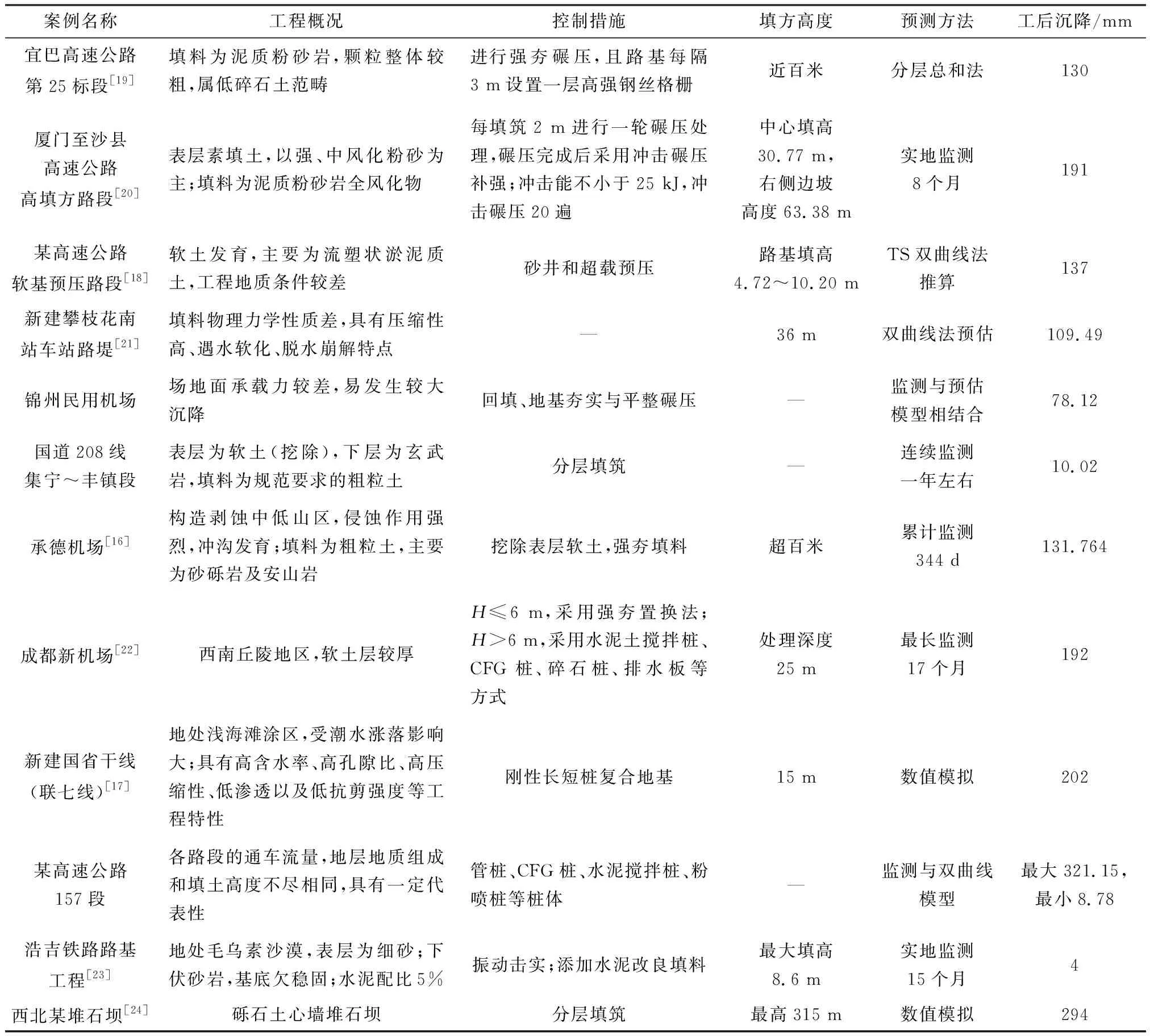
表3 高填方工程案例Table 3 Cases of high fill engineering
一般认为填方体高度是工后沉降的主控因素,图1为各工程案例的沉降稳定值随填方体高度变化情况。由图1可知,沉降量和填方高度并没有明显的正相关关系,这说明填方工程的施工质量和控制措施对工后沉降影响较大。良好的填方工程,即使填筑高度很高,但是沉降并不大,例如承德机场[16]工程填方近百米,沉降只有130 mm。但如果工程措施采取不当则会导致大幅沉降,例如联七线填筑高度仅15 m[17],其长期工后沉降达到了202 mm。
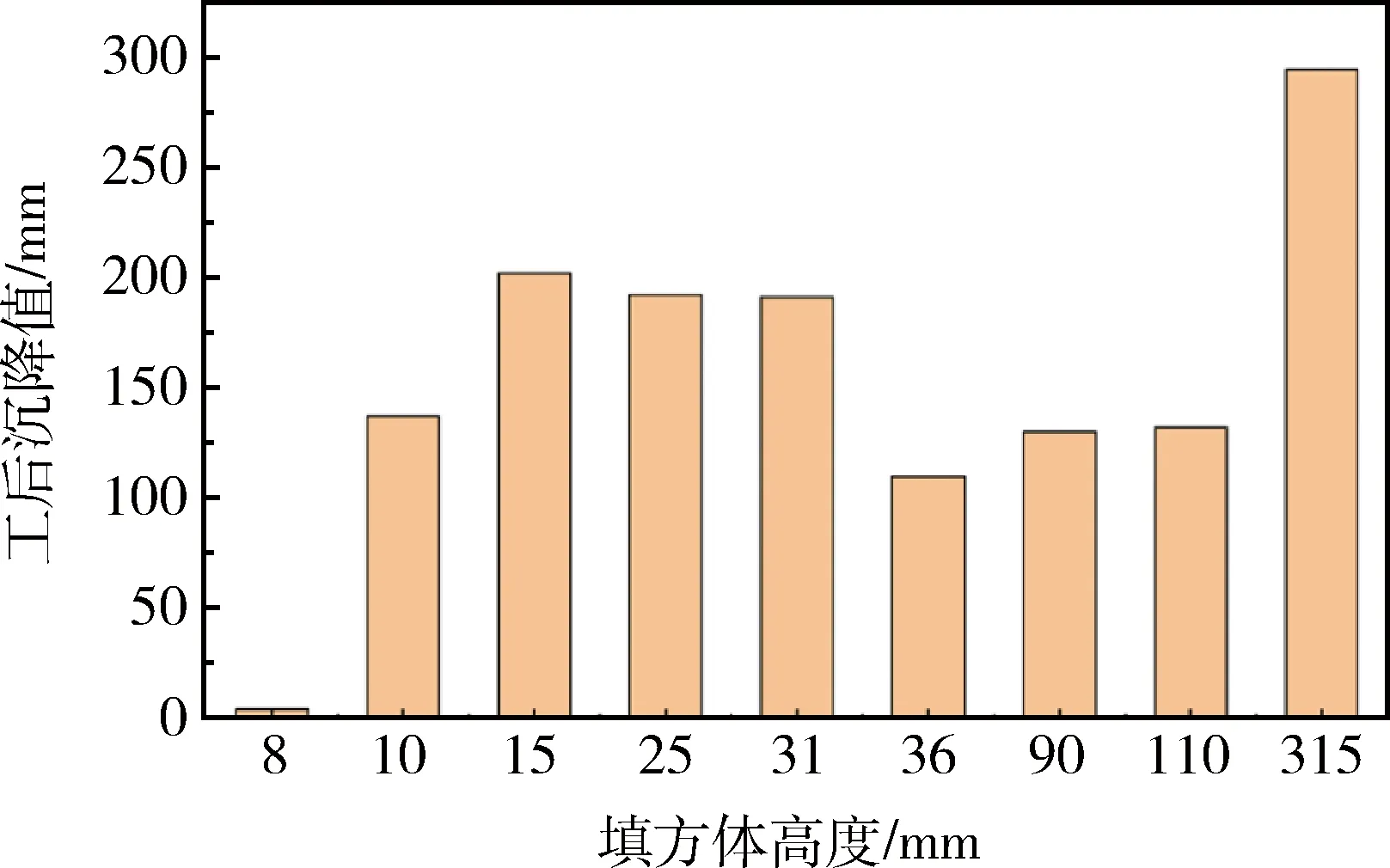
图1 不同填方高度工后沉降变化情况Fig.1 Post-construction settlement changesof different fill heights(资料来源:文献[16]~文献[24])
另外,以上案例的调研结果表明,影响工后沉降最主要的因素是土体类型。图2为上述案例中不同土体类型条件下各工点每米沉降量的计算结果。由图2可知,软土地基工点每米产生的沉降值远大于岩质填料工点的沉降值,其中某高速公路软基预压路段[18]每米沉降接近14 mm。在实际施工中,若高填方路段施工前的地表存在软土层,会严重影响工后沉降的稳定值,因此当软土层厚度较小时,应尽可能挖除。
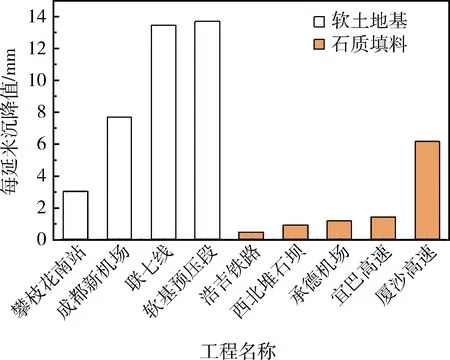
图2 不同土类型工后沉降变化情况Fig.2 Post-construction settlement changesof different soil types(资料来源:文献[16]~文献[24])
3 高填方工程工后沉降机理与诱因
高填方工后沉降可以概括为荷载作用下产生的蠕变沉降、干湿循环产生的湿陷性沉降、细粒土排水产生的固结沉降、掺合料失水产生的干缩沉降[2,25-26],可用式(1)表示。
S=Sc+Sw+Si+Sd
(1)
式中:S为总沉降;Sc为荷载作用下产生的蠕变沉降;Sw为干湿循环产生的湿陷性沉降;Si为细粒土排水产生的固结沉降;Sd为掺合料失水产生的干缩沉降。由于高填方工程的土体类型不同,式(1)中4个部分的贡献不同,其中粗粒土以Sc、Sw为主;而细粒土以Si、Sd为主。
3.1 粗粒土高填方工程工后沉降机理
粗粒土填料所含黏性成分少,内部孔隙通常较大,这意味着排水固结沉降在较短时间内即可完成[2]。因此,对于粗粒土填料,其长期工后沉降主要由Sc和Sw两部分组成,可表示为式(2)。
S=Sc+Sw
(2)
首先,粗粒土在上部荷载作用下发生颗粒破碎,破碎之后产生的细粒沿着新生成的大孔隙移动,同时引起应力重分布,产生常规蠕变沉降。其次,工后十余年中,晴雨循环、河水反复升降所引起的干湿循环,季节变化、昼夜更替所引起的温度循环等外部因素产生湿陷沉降。王海俊等[25]认为由干湿循环造成的湿陷性沉降是工后沉降最主要的组成部分,经过河水或雨水的反复浸润,导致土体颗粒接触面的抗剪强度降低,打破原有的颗粒平衡,引起剪切破坏,从而诱发较大湿陷沉降。
3.2 细粒土高填方工程工后沉降机理
对于细粒土填料,其长期工后沉降主要由Si组成,即式(3)。
S=Si
(3)
软土类型的土体,颗粒之间孔隙小,所含黏性成分较多,使得排水固结沉降延续时间较长。当土体饱和时,在上部荷载作用下,将产生超静孔隙水压力。 施工完成后,随着孔隙水缓慢排出,超静孔隙水压力逐渐消散,孔隙体积逐渐减小,进而产生固结沉降。
另外,当细粒土填料的强度不符合规范要求时,需添加掺合料(如水泥、沥青等)对填料土体进行改良。填料所在的环境发生变化时,掺合料中的水分蒸发过多,失水干燥,会引起其体积收缩甚至开裂,从而产生干缩沉降[26]。因此,对于细粒改良土,其高填方工后沉降以干缩沉降为主。
4 高填方工程工后沉降预测方法
高填方工程的工后长期沉降观测成本高、周期长。因此,对高填方工程的工后沉降进行计算和预测非常重要,也是目前研究的重点内容。目前高填方工程工后沉降的计算和预测方法,主要包括以下几个类型。
4.1 细粒土高填方工程工后沉降计算理论模型
对于软土而言,目前计算饱和土体在荷载作用下固结沉降的理论较为完善,以太沙基固结理论为基础,通过理论推导,可以得到工程中实用的简便计算方法。现行规范《建筑地基基础设计规范》(GB 50007—2011)[27]中,基于一维压缩理论给出了分层总和法的简化计算公式见式(4)。
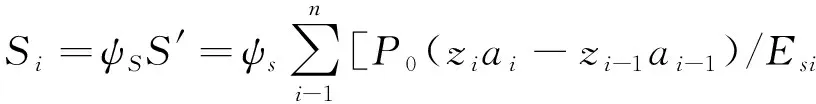
(4)
式中:ψs为沉降计算经验系数;S′为分层总和法计算的地基沉降量;n为划分的土层数;P0为基底附加应力;Es为压缩模量;zi为第i层至基底距离;ai为第i层平均附加应力系数。
式(4)的方法沉降计算结果受沉降计算经验系数取值的影响很大,实际应用的时候,经常会存在较大的误差。为此,魏汝龙[28]曾提出一种基于EC-p曲线的地基沉降计算方法。ε-p曲线近似于双曲线,因此ε/p-p曲线可以近似看作直线,ε/p即为ε-p曲线的割线模量(EC),该直线方程见式(5)。
EC=E0+mp
(5)
将式(5)代入沉降计算公式,即可得最终公式,见式(6)。
Si=(P2/EC1-P1/EC1)ΔH=
E0ΔPΔH/[(E0+mP1)(E0+mP2)]
(6)
式中:m为EC-p曲线的斜率;E0为初始模量;ΔH为土体高。
魏汝龙[28]提出的上述割线模量法虽然与分层总和法所需试验数据相同,但计算误差相对较小。此后,丁洲祥等[29]从压缩变形机理着手,对割线模量法进行了改进,在进行计算时引入了修正系数α,计算见式(7)。
a=(1+eA)/(1+e0)
(7)
式中:eA为A点孔隙比;e0为初始孔隙比。
将式(7)带入沉降计算公式中可得式(8)。
Si′=Si/α
(8)
式中,Si′为改进后的沉降值。
该方法不再将ε-p曲线近似看作双曲线,计算结果比改进前更精确。
4.2 粗粒土高填方工程工后沉降估算经验模型
对于粗粒土填料工程,尚缺少相关的理论计算模型。为此,实际工程中多采用工程类比法,通过借鉴其他高填方工程(如某些已完工的堆石坝、机场、路基等)的经验公式来预测工后沉降。此类方法主要基于前期的现场实测数据或室内模型试验数据进行[30-31],数据越详实测量周期越长,则预测结果越趋于精确[32]。此类方法在堆石坝设计中应用较多,其中具有代表性的工作如下所述。
1) 傅志安[33]认为在河谷形状近似情况下,可采用式(9)类比。
S2=(H2/H1)2×(E1/E2)×S1
(9)
式中:S2为未建大坝的沉降预测值;S1为已建大坝的沉降观测值;E2为未建大坝的变形模量;E1为已建大坝的变形模量;H2为未建大坝的坝高;H1为已建大坝的坝高。该公式计算简单,使用方便,但仅考虑了坝高与坝体材料的变形模量,并未考虑河流水位、时间等的影响。
2) 顾慰慈[34]将堆石坝总沉降分为施工期沉降与运用期沉降。根据哥以奇坝等8座堆石坝的沉降观测值,得到施工期沉降预测近似公式见式(10)。
S0=0.149 6H1.646
(10)
式中:S0为施工期沉降;H为堆石坝高度。该公式的施工期沉降预测值仅与坝体高度有关,且仅仅适用于碾压法及振动碾压法施工的堆石坝,有一定的局限性。此外,对于运行期沉降,顾慰慈根据国外63座堆石坝的实测沉降资料,采用回归分析方法进行研究,得到沉降计算经验公式见式(11)。
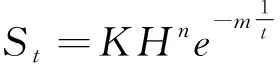
(11)
式中:St为堆石坝运行t年后的沉降量;H为坝高;t为自堆石坝开始运行时算起的年数;K、n、m为系数,与坝型有关。式(11)为回归分析之后得到的指数型函数,考虑了坝高、坝型以及时间等影响,分析因素较为全面。
3) 闫生存等[35]认为高面板堆石坝施工时通常分多期进行浇筑,蓄水高度与浇筑进程同步进行,故对下部填筑体而言,填筑高度与水压处于动态变化之中,预测沉降量时需考虑这部分分量,并通过统计分析提出式(12)。
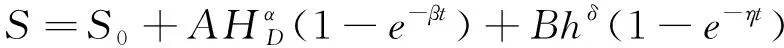
(12)
式中:S0为漏测沉降量;HD为填筑高度;h为水压分量;t为时间;A、B、α、β、δ、η为统计参数。式(12)考虑的因素较为全面,但需要应用已有成功施工经验与大量实测数据进行统计分析,且计算过程较为复杂。
RAKSIRI等[36]认为堆石坝沉降与坝体形状有关,并根据工程经验提出经验公式见式(13)和式(14)。
S=a-b×cSβ
(13)
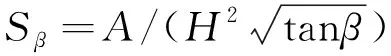
(14)
式中:A为混凝土面板面积;H为坝体高度;β为坝坡仰角;a、b和c为常数且分别取值为16.49、28.45和0.42。
4.3 高填方工程工后沉降数值模拟计算方法
随着计算机技术的发展,以固结理论为基础的有限元软件应运而生,如Midas软件、Plaxis3D软件、Comsol软件等。相比于现场监测,借助这些有限元软件可以开展高填方工程工后沉降的数值模拟计算[37-43]。这类方法对计算细粒土排水产生的固结沉降Si较为成熟可靠,但是需借助室内试验测得建立模型所需的参数,参数的准确性对数值模拟的准确性至关重要。
近年来,该方法在蠕变计算方面也取得了一定的突破[44]。姚仰平等[45]推导出了高填方工程蠕变沉降实用本构模型,可用于蠕变问题的有限元计算。该模型将填方体与原地基看作一个整体,简化边界条件,忽略侧向变形,在考虑时间效应的UH模型中引入弹性压缩线,可得最终计算模型见式(15)。
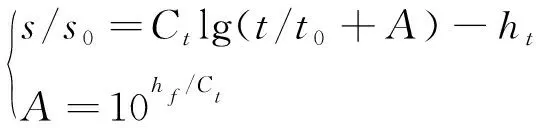
(15)
式中:S0为单位蠕变量,S0=1 mm;hf为无量纲参数,反映土体超固结程度;Ct为无量纲参数,反应蠕变速度;A为过渡参数;t为蠕变时间;t0为无量纲参数,t0=1 d。该模型成功应用于承德机场工后沉降计算分析,预测结果与实测值吻合良好。
针对式(1)有另外两项变形,即干湿循环产生的湿陷性沉降Sw和填料失水产生的干缩沉降Sd,目前数值模拟计算方法尚缺少成熟的方法,未能在高填方工程获得成功应用,是未来值得努力的方向,主要的问题是缺少相应的本构模型和实验数据。
4.4 基于回归分析和人工智能的高填方工程工后沉降预测
根据已测得的短期监测数据进行曲线拟合,以预测长期工后沉降,简单直观且方便实用。 在高填方工程的工后沉降监测方面,随着科技的进步,监测方式也日新月异,例如EMADALI等[46]使用TerraSAR-X聚光雷达影像分析了伊朗某堆石坝的工后沉降变形。
常用的方法有幂函数法、Asaoka法、指数法、双曲线法、对数法等[47-50]。SIMES等[51]对巴西某垃圾填埋场进行沉降预测时,借助流变模型与双曲线模型计算最终沉降值。通过对比沉降实测值发现,这两种模型均明显低估了沉降值,准确性不高。魏道凯等[52]基于武汉天河机场高速公路的实测数据,对比分析了双曲线法、指数法和Asaoka法三种方法,发现指数法精度最高。刘兵[53]在同一工程案例中将曲线拟合法及FLAC3D数值模拟法进行对比分析,得出指数法误差最小的结论。
近年来,人工智能预测模型发展迅速,也在高填方工程的工后沉降预测上取得了一些突破,代表性的工作主要有以下几个模型。
1) 灰色理论预测模型。王禄洲等[54]在进行昔格达层高填方路基沉降预测时,分别使用了曲线拟合法和灰色系统法。预测结果表明,这两种方法与实测数据拟合良好,可为类似工程提供借鉴。有学者基于太原市太行路阎家峰路段的高填方路段实测资料,运用灰色理论建立均值GM(1,1)模型,对施工期沉降和工后沉降分别进行预测。结果表明,该模型特别适用于对工后沉降的长时间预测。冯国建[55]进行沉降预测时使用灰色理论,建立不等时距残差GM(1,1)模型和灰色Verhulst模型两种模型,对沉降进行预测并对结果进行比较。结果表明,两种预测曲线与实测数据曲线吻合良好。
2) 神经网络预测模型。KIM等[56]建立了预测堆石坝坝顶相对沉降的神经网络模型,该模型使用来自7个国家的30个工程的监测数据库,能够较好地预测不同工况下的堆石坝工后沉降。然而高填方路基的工后沉降受到多因素的综合影响,且变形持续时间长,预测结果与十余年后的实际工后沉降仍存在一定偏差。人工智能预测模型在这方面虽然具有较强的潜力,但是受制于目前的数据积累水平,人工智能预测模型尚未超越传统方法所能获得的精度,要想继续发展人工智能预测模型必须做好长期观测、数据收集、数据库建设等工作。
5 高填方工程工后沉降控制措施
为了减少高填方工程的工后沉降变形,需要采取针对性的施工工艺,必要时还需对软土填料进行处理。目前,施工中最常用的变形控制方法主要包括以下几种。
1) 做好防排水设施。工后沉降的产生与土体中的含水量关系密切,防排水措施对于减小工后沉降尤为重要。工程中需要采用坡面防水与填方体排水相结合的水分控制技术,保持粗粒土路基填料的干燥。目前,施工技术较为成熟且常用的防水、排水措施包括以下几方面。①坡面防水以阻止地表水入渗为主,配合盲沟、急流槽、截水沟以及地表排水管道系统等排水设施[57-60]。吴羊[60]提出一种新型水分控制技术,即利用毛细阻滞覆盖层,来防止地表水下渗,如图3所示。该技术基于非饱和土渗流理论,采用细粒土上覆于粗粒土形成毛细阻隔带,通过粗粒土、细粒土之间的基质吸力差阻滞地表水的入渗。对于堆石坝的防水排水,宽级配砾质土目前已较为常用。 史新等[61]通过试验研究认为细粒含量30%~40%时,其防水效果最佳。
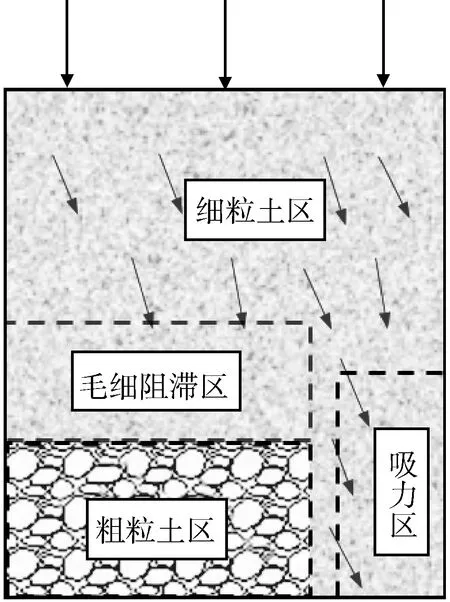
图3 毛细阻滞覆盖层Fig.3 Capillary blocking coating
②为保持粗粒土填料干燥,需进行填方体内部排水。工程中一般使用水平砂垫层以及竖向的排水结构。此外,也可采用一种新型排水材料(即毛细透排水管)。这是近年我国台湾技术人员开发的一种新型排水材料,其排水通道横截面形如字母“Ω”,不仅能主动排水,还能有效防止土颗粒流失[62-64]。延安新区位于黄土丘陵沟壑区,经常会遇到高填方工程,地质情况复杂,且由于黄土的湿陷性,需严格控制地下水以及地表水入渗的影响。基于此类复杂工况下的高填方工程,有学者提出“三面二体一水”控制论。该控制理论紧紧围绕易发生工后沉降的六个敏感要素,即填筑体顶面、侧临空面、填挖交接面(三面),填筑体、原地基体(二体),地下水与地表水及其相互转化(一水),如图4所示。在实际施工中,对这六个关键部位的施工质量进行严格控制,则整个复合系统的工后沉降便可得到有效控制。
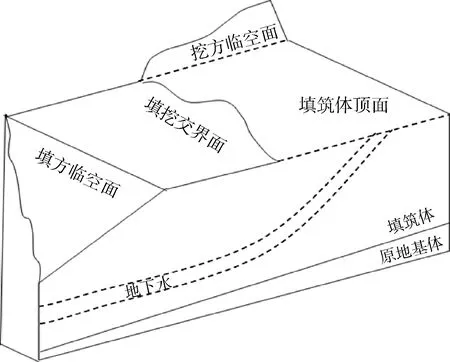
图4 “三面二体一水”示意图Fig.4 Schematic diagram of “three sides,two bodies and one water”
2) 细致进行土体压实工作,减少土体压缩性。填方体压缩性越大,其工后沉降越多,由于高填方工程上覆荷载较大,因此对压实工作提出了更高的要求。常用方法有分层填筑法、自然固结法、冲击碾压补强法、真空预压法等[65-66]。提高施工期的验收标准,严格控制施工期沉降措施才是能从根本上解决问题。如果在运营期出现工后沉降过大的问题,可以采取换填土法、布设土工格栅法、灌浆法等[67-69]等方法进行补救。
3) 必要时需对软土填料进行处理。当高填方路段存在软土地基时,需对软土地基进行加固处理,以保证原地基的承载能力。当软土层厚度较小时,可进行直接换填或挖除[70];当软土层较厚时,常用处理方法有强夯补强法、强夯置换法、CFG桩、碎石桩法、真空预压法、超载预压法等[71-76]。在沿海地区,软土层通常较厚,受海水潮汐引起的干湿循环影响大,且力学性质较差,通常需要高桩加固地基,例如荷兰的Reeuwijk沿海公路路基[77]。
6 结 语
随着高填方路基、机场、堆石坝等工程的大量修筑,施工技术趋于成熟,为此后高填方工程的修建积累了大量经验。如果采取合理的措施,可以将高填方工程的工后沉降控制到容许范围之内。但是如果低估工后沉降的严重性,未采取针对性措施,高填方工程的工后沉降将非常可观,影响到构筑物的安全运行。
对于高填方工程,土体类型是影响其工后沉降的主控因素。对于细粒土高填方工程而言,沉降变形主要来源于固结变形和干缩变形。目前,对于固结变形已有较成熟的计算理论和方法,但是对于干缩变形尚缺少相应的计算理论和方法,是未来努力的重点。对于粗粒土高填方工程而言,变形主要来源于蠕变变形和湿陷变形。其中,蠕变变形计算近年取得了突破,但是对于湿陷变形,目前尚缺少合理的计算模型和方法,是有待攻克的一个难题。另外,在高填方工程工后沉降预测方面,近年经验方法和人工智能方法都取得了长足的进步,积累了一定的数据和经验。其中人工智能方法在高填方工程工后沉降预测方法具有较大的潜力,但是面临着数据积累不足的问题,模型潜力无法充分发挥和挖掘的困难。

