内蒙古东乌旗地区激发极化法精细化反演方法研究

潘北斗

(1.中国冶金地质总局 第一地质勘查院,燕郊 065201；2.中国冶金地质总局 矿产资源研究院，北京 101300)

0 引言

内蒙古东乌旗地区主要有斑岩型、侵染型矿床的钼矿，热液脉状、热液蚀变型矿床的银铅锌矿，矽卡岩型矿床的铁锌矿等[1-2]。找矿标志几乎都是金属硫化物，而金属硫化物较之于围岩有较强的激电效应[3-4]。2001年至今第一地质勘查院在东乌旗地区开展了大量的激电工作。在阿尔哈达、迪彦钦阿木和花脑特等矿区取得了较好的找矿成果,而在其他矿区没有突破性找矿成果，其主要原因之一是物探工作的多样性、反演解释的多解性和反演精度的不稳定性造成的[5-7]。依据本次研究工作目标和工作内容，综合研究区的具体情况，确定本次研究工作技术路线。研究利用相关资料、通过软件进行数值分析，推导出激电异常相对于目标体真实空间位置的偏移量(Δa)与目标体埋深(h0)、测量极距(AN)之间的关系，对模型加以修改，并找出影响模型的相关因素定量分析，通过实际运用对其可行性和实用效果加以客观评价，结合本区情况提出下一步找矿方向。项目研究的总体技术路线见图1。

1 激发极化法反演问题

地球物理反演是通过地球物理异常的分布特征确定地质体的赋存状态，即在数学基础上，通过实际观测值使其与模型理论值达到最大限度的拟合，以此来求解地球物理模型。

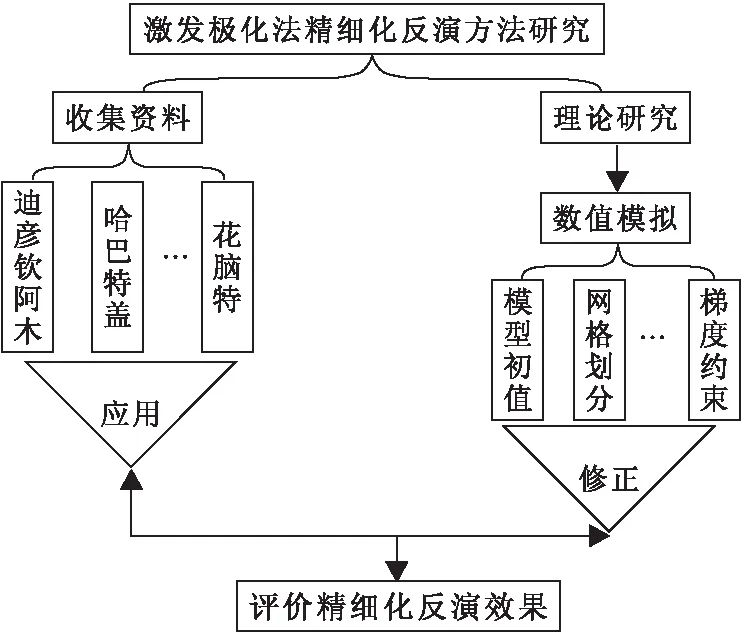
图1 技术路线图Fig.1 Technology roadmap

1.1 广义线性反演

通常把地球物理反演问题用一个泛涵方程组表示，其离散化后取得一些非线性方程组，但是地球物理数据是有限的，地球物理的解通常具有多解性，此时只能使用某种可接受的解估计，该方法称为广义反演方法，利用泰勒级数展开的形式形成的方程组反演方法都称为广义线性反演[8]。

1.2 时间域激发极化原理

时间域激电法作为电法勘探的重要分支，广泛应用在资源勘查中，通过人工场向地下以脉冲直流供电，并以一种装置的形式对地下电流的分布规律和激发效应进行观测研究，通过反演得出异常体的埋深、产状和位置等，从而查明矿产资源赋存状态和地下地质体情况[9-10]。

1.3 激发极化法的数值模拟

随着电子计算技术的飞速发展，为电场的数值模拟提供了技术支撑，使之得以实现。目前，国内、外已经有一些学者和单位，广泛地将数值模拟技术应用于研究激电异常，用来对稳定电流场作数值模拟的方法主要采用有限单元法和有限差分法。其中有限差分法一般适用于小规模模拟计算，而有限单元法通常用于大型模型分析。

在激电法模拟中，利用有限单元法求解地电断面为真电阻率和有效电阻率分布时的稳定电流场，再依据等效电阻率法计算激电异常[11]。

1.4 最小二乘约束反演方法

地球物理反演是非线性的，病态的，反演解释存在多解性以及非唯一性。目前比较成功的做法是将光滑约束、先验信息等加入反演算法中，建立基于某种约束的最小二乘反演算法。

非线性问题线性化，并引入光滑约束和已知先验信息，构造出最小二乘反演目标函数为式(1)[12-13]。

ψ=‖Wd(δd-Aδm)‖2+

‖Wm(m-m0+δm)‖2

(1)

式中：‖Wd(δd-Aδm)‖2为常规的最小二乘法;‖Wm(m-m0+δm)‖2为先验信息项。其中，δd为数据残差矢量，其值为实测数据对数值与模型正演计算数据对数值之差；m为预测模型向量，其值为模型参数的对数值；m0为基本模型向量，其值为模型参数的对数值；A为偏导数矩阵；Wd为观测数据加权矩阵。Wm为称模型加权矩阵。目标函数式对δm求导，并令其等于零,解线性方程组便可得模型参数带约束条件时的最小二乘反演结果。

2 精细化模型反演研究

由于激电测量受体积效应的影响，激电异常往往是各种异常的叠加反应，随着极距的增大，探测成果中叠加的上部异常信息越多，反演解释难度随之增大。精细化反演处理的目的是通过反演将深部的叠加异常信息分离开来，从而获得异常源的有效信息。精细化反演的特征是力求同时使观测数据与计算数据间的差值、背景与反演模拟参数间的差值以及反演模拟粗糙度最小化，通常利用均方根误差准则量度数值的拟合性，偏离先前模拟的距离以及模拟粗糙度。设计如图2和图3所示的简单模型来进行激电测深精细化反演模拟。

图2 电阻率模型Fig.2 Resistivity model

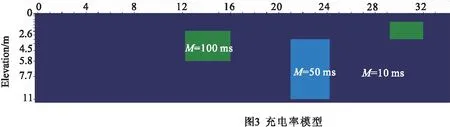
图3 充电率模型Fig.3 Charging rate model

2.1 有限元网格的选择

2.1.1 初始模型层数

一般来讲，当保持网格内单元格大小不变情况下，网格越大越好；反之保持网格不变情况下，单元格越小越好，这两种情况下都会增加大量的计算工作量。为了解决精度和工作量之间的矛盾，往往采用非均匀网格，即网格中心单元小、节点密，边界单元大、节点稀，由中心到边缘单元逐渐放大。优点是在保证了网格有足够的大小前提下，又保证地电断面的复杂部位位于网格中心，从而满足求解要求。反演实践中通常会给定一组初始模型作为拟合初值，假定为层状地电结构，从表层向深部层厚依次增加，增加比例在1.01～1.5之间，首层厚度一般设置为0.3电极距，保证模拟深度不小于实际探测深度。

反演采用了10层(图4)、20层(图5)、30层(图6)模型进行拟合。从反演结果看，10层模型反演结果比较粗糙，尤其是下部控制稀疏，已经形成拖拽现象，造成异常放大，显然不足以拟合观测数据，20层与30层模型反演结果区别不大，由此可以推定，20层模型已经完全可以拟合观测数据。

图4 10层模型的反演结果Fig.4 Inversion results of 10-layer model(a)电阻率模型;(b)充电率模型

图5 20层模型的反演结果Fig.5 Inversion results of 20-layer model(a)电阻率模型;(b)充电率模型

图6 30层模型的反演结果Fig.6 Inversion results of 30-layer model(a)电阻率模型;(b)充电率模型

2.1.2 网格密度

网格密度增大会提高计算精度，但会增加计算规模，所以在工作中要综合这两个因素考虑。网格较少时，在计算时间增加不大的情况下，通过增加网格数量提高计算精度提高。当网格密度增加到一定程度后，再继续增加时精度提高很小，网格密度应增加到计算结果在误差允许范围以内便可。在网格密度上分别采用了等倍电极距(510个模块)图7，0.5倍电极距(1 020个模块)图8和0.25倍电极距(2 040个模块)图9进行反演，从反演结果看，等倍电极距的横向分辨率不够，造成了异常横向拉长，低充电率区域被掩盖，0.5倍电极距和0.25倍电极距在异常显示上并没有较大形变，但是0.25倍电极距断面图引入了许多虚假细节，反演结果不够光滑，这是过拟合地反映。

图7 等电极距划分510个模块的反演Fig.7 Inversion results of 510 modules divided by equidistant electrodes(a)电阻率模型;(b)充电率模型

图8 0.5电极距划分1 020个模块的反演Fig.8 Inversion results of 1 020 modules divided by 0.5 electrode spacing(a)电阻率模型;(b)充电率模型

图9 0.25电极距划分2 040个模块的反演结果Fig.9 Inversion results of 2 040 modules divided by 0.25 electrode spacing(a)电阻率模型;(b)充电率模型

2.2 平滑度约束

平滑度约束是反演模型的重要参数，拟合观测数据和维持平滑度变化是反演过程当中同时需要考虑的。如果一个新模型非常平滑，但其计算数据不能与野外数据很好拟合，则这个反演是失败的，然而一味追求数据拟合度则会使得模型断面失去趋势性，过多的虚假异常往往会掩盖了目标异常。这时候可试用一定范围的模拟约束权值进行反演，改变数据拟合与维持平滑模拟间的折中，直到用较低的模拟约束权产生对观测数据的完美拟合，要避免过高约束形成的粗糙模型和过低约束形成的过拟合现象。

反演采用了0.1(图10)、1(图11)和10(图12)作为平滑约束因子。从反演结果来看:0.1的反演结果几乎没有平滑约束，数据有很大的灵活性，结果形成类一维地电结构，二维约束缺失；平滑因子为10的结果过多地模糊了细节异常，两个水平的异常体不能分辨，显然对于精细化反演来讲是背道而驰的，平滑因子为1的结果则显示了较好的平滑折中，达到了精细反演的目的。

图10 无平滑约束的反演结果(平滑因子0.1)Fig.10 Inversion results without smoothing constraints (smoothing factor 0.1)(a)电阻率模型;(b)充电率模型

图11 适度平滑约束的反演结果(平滑因子1)Fig.11 Inversion results of moderate smoothing constraints (smoothing factor 1)(a)电阻率模型;(b)充电率模型

图12 过度平滑约束的反演结果(平滑因子10)Fig.12 Inversion results of excessive smoothing constraints (smoothing factor 10)(a)电阻率模型;(b)充电率模型

图13 5次迭代的反演结果Fig.13 The inversion results of 5 iterations(a)电阻率模型;(b)充电率模型

图14 20次迭代的反演结果Fig.14 Inversion results of 20 iterations(a)电阻率模型;(b)充电率模型

2.3 收敛标准

收敛标准是影响反演结果的主要因素，主要指标是最小残差，通常以百分比来衡量。如果残差大于10%即可认为反演的可信度较低，百分比通常是越小越好。但是这将需要较长的反演时间，最好地反演是能在最小残差和观测数据拟合约束间找到平衡。这需要在反演迭代次数，最小步长和最小残差上的多次试验，以找到合理的拟合模型，从而改善反演结果。

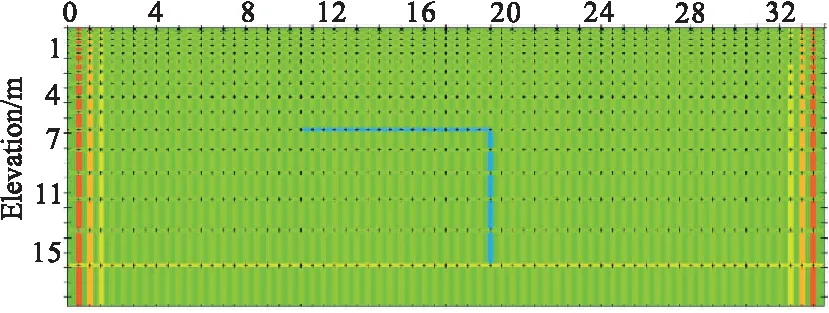
图15 梯度约束控制图Fig.15 Gradient constrained control chart

反演实践中迭代3次以上即可以得到拟合模型的大致轮廓，随着迭代次数的增加，反演精度有明显提高。图13、图14中使用1%残差和1.5%步长分别迭代5次与20次的结果，图13所示5次迭代的模型虽然显示了主要异常，但是分辨率很低，模型粗糙，迭代20次的结果较完美的还原了原始模型，可见多次迭代可以有效改善迭代效果。

2.4 梯度约束

在某些已知地质条件的情况下，初步反演之后，在明显高对比度接触带的模型断面区域，引入梯度约束来切断平滑度约束是有益的。尤其在取得了钻孔资料后，有必要在钻孔部位约束反演，这可以大大减少反演的多解性，在一些导电覆盖区则必须进行梯度约束来抵制低阻屏蔽的影响。初步反演能给出浅部信息的良好指示，但是平滑度约束与电法体积效应的作用可能模糊深部特征。因此在数据灵敏度降低的深部切断平滑度约束，然后重新反演可改善深部特征的分辨力，这可使得基岩或者接触带类型的激电异常变得更加明显。

鉴于低阻的拖拽效应，笔者在低阻下方和高低阻接触带部位编辑梯度约束。从图16可以看出，低阻和高低阻接触部位得到了很好的约束，准确地反映了原始模型的结构，反演效果良好。

图16 带梯度约束的反演结果Fig.16 Inversion results with gradient constraints(a)电阻率模型;(b)充电率模型

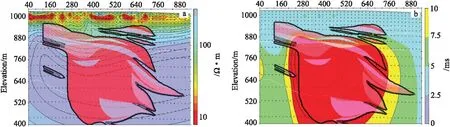
图17 69线反演结果Fig.17 Inversion results of 69 lin(a)电阻率;(b)充电率

3 精细化反演

3.1 迪彦钦阿木激电测深精细化反演

根据已知资料，选取较有代表性的69线激电测深工作来研究。由钻孔资料得知，ZK6904和ZK6903钻孔见矿位置围岩主要为凝灰岩和安山岩等。由图17可以看出，69线地电结构比较简单，浅部激电等值线比较平缓，视电阻率偏低，与第四系埋深较厚有关；深部特征比较明显，其中视电阻率在剖面两侧较高，中间相对低。充电率在形态上呈现“桃”状形态，测线大号方向衰减较快，异常体中间稍有凹陷，与已控制的矿体比较，反演充电率和矿(化)体吻合很好，矿体细节形态也有显现，精细化反演效果良好。

从图18可以看出， 21线地电结构比较复杂，第四系埋深较浅，深部横向上高低阻相间，形态复杂，充电率向大小号方向放射，底部有凹陷和已控制矿体对比，总体形态吻合，但是已控制矿体形态异常复杂，矿体多呈细脉状，反演断面对细节的显示有限，说明精细化反演对于复杂断面的反演仍然有待提高。

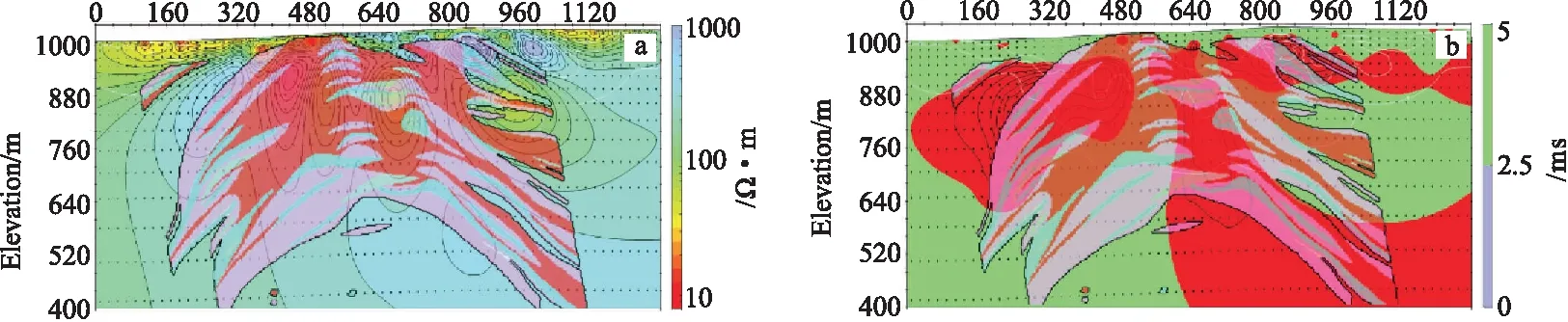
图18 21线反演结果Fig.18 Inversion results of 21 line(a)电阻率;(b)充电率

3.2 哈巴特盖激电测深精细化反演

2014年哈巴特盖工区共完成激电测深剖面6条，其中在19线进行了工程验证。在19线点号920处施工钻孔，孔深为400.70 m，全孔共分4层，地层上部主要为安格尔音乌拉组角岩化砂岩，9.20 m～54.85 m为氧化带，岩心几处破碎较强，具褐铁矿化，54.85 m～302.90 m为砂岩原生带，多处云英岩脉穿插，厚度为0.3 m～8 m不等。与原岩接触面中轴夹角为30°～50°。下部302.90 m～400.70 m为花岗岩体，中粗粒至细粒不等。

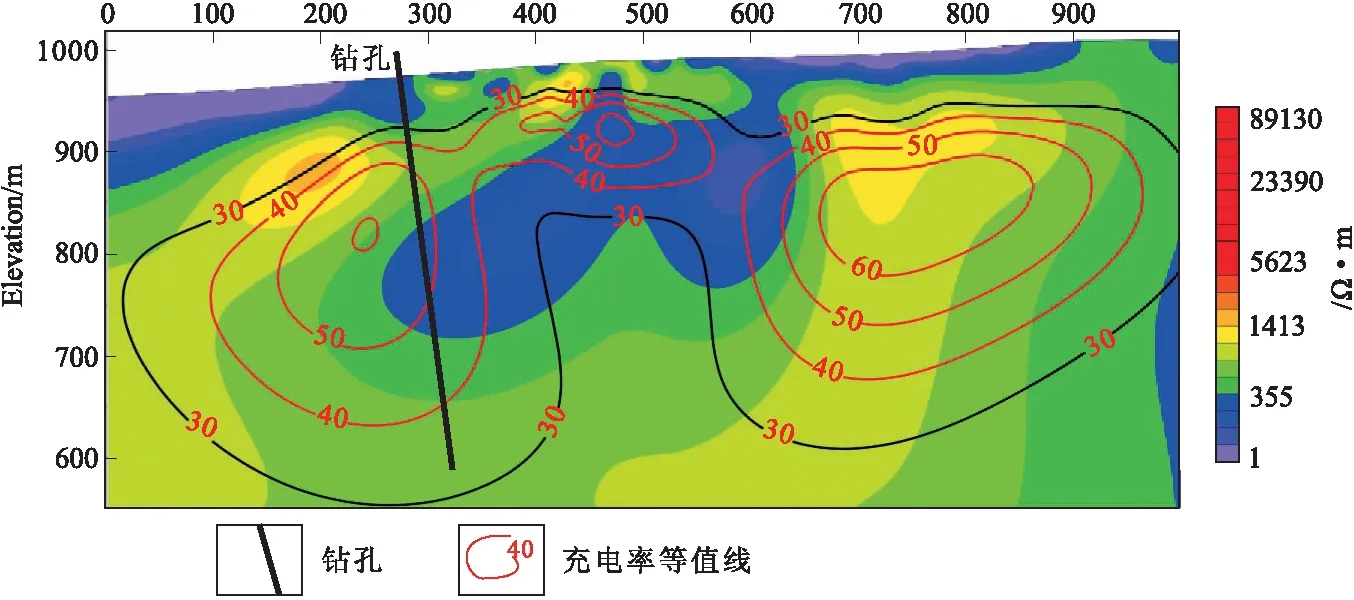
图19 19线反演结果Fig.19 Inversion results of 19 line

在已有钻孔资料的基础上，对原有数据进行了精细化重新反演，从图20可以看出，中部的低阻凹陷有了较大的变化，且充电率形态有了细节反映，新断面也与已知钻孔吻合，可见精细化反演对本条测线有较大地改善。

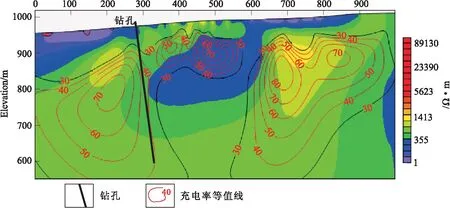
图20 19线精细化反演结果Fig.20 Refined inversion results of 19 line

4 结果与讨论

4.1 精细化反演选择

1)网格选择。在划分网格时一般采用非均匀网格，网格的中心部分单元小，节点密，边界单元大，节点稀，由中心到边缘单元逐渐放大，初始模型层数建议一般不少于16层，过少的层数会使拟合模型非常粗糙，然而过多的层数对精细化反演改善并不大，且反演消耗将会指数增加，甚至产生假异常，横向上最少要保持半极距分辨力以上的网格数量才能保证拟合的准确度。

2)平滑度选择。平滑过高会导致计算数据不能与野外数据很好拟合，最终形成简单粗糙的模型，较低的平滑度会提高数据拟合度，但同时引入噪声与假异常，通常需要在这两者之间选择折中。

3)收敛标准。收敛标准以数据拟合误差作为评价，在平滑度保证的前提下拟合误差越小越好，但是误差设置过小可能会造成模型不收敛，在设置误差门槛的过程中迭代次数和搜索步长是两个关键参数，实践证明搜索步长维持在1%，迭代次数在5次以上，大多数情况下模型拟合残差会小于5%，而且迭代次数在20次以上会对反演结果有一定改善，更多的迭代会消耗大量资源，且改善效果不明显。

4)梯度约束。在已知地质条件的情况下，或者断面内有钻孔资料后，引入梯度约束的效果是明显的。另外一种情况是在一些导电覆盖区进行梯度约束来抵制低阻屏蔽的影响。在初步反演之后，在明显梯度带部位编辑梯度约束重新反演，能更好地修正反演结果，可使接触带类型的激电异常变得更加明显。

4.2 关于过拟合

1)进行精细化反演之前，物探数据的预处理显得尤为重要，如果反演数据存在较多噪音干扰，这将使精细化工作变得异常困难，更有可能反演出假异常，数据的前期滤波就变得重要了。

2)目前的反演软件通常以不等边四边形作为网格划分，在进行反演时充分考虑数据灵敏度和分辨率宽度，可以提供合理的网格划分思路，一味追求细分网格不仅会使反演开销成倍增长，而且会使得噪声和假异常泛滥，这种过拟合现象对反演弊大于利。

3)平滑度对反演的控制异常重要，追求数据拟合度往往形成过拟合反演模型，从而淹没主要异常，使反演结果变得难以分辨。

5 结论

笔者分别从有限元网格、平滑度约束、收敛标准、梯度约束等几方面研究，对精细化反演做了深入探索，主要得出以下结论。

1)网格划分时一般采用非均匀网格，即网格的中心部分单元小，节点密，边界单元大，节点稀，由中心到边缘单元逐渐放大；平滑度不宜过高也不宜太低，通常需要在两者之间选择折中；在平滑度保证的前提下拟合误差越小越好，但误差设置不能过小，以免造成模型不收敛。

2)在已知地质条件的情况下，引入梯度约束能够明显提高反演精度。

3)复杂的地电结构仍然是困扰反演精度的主要因素，后续研究将针对这些问题进行改进。