基于能量传递规律的油茶树冠层振动参数优化与试验

伍德林 赵恩龙 姜 山 王韦韦 袁嘉豪 王 奎

(安徽农业大学工学院， 合肥 230036)

0 引言

油茶是我国特有的油料作物，近年来我国油茶产业发展迅猛，种植面积达到4.364 53×106hm2，茶油产量达到6.7×104t[1-3]。随着我国机械化的快速发展，高强度的农业劳作逐渐被机器取代，林果的收获作业正处在从人工到半机械、机械化的演变过程中[4-6]。振动方式已被证明是林果机械化收获作业的有效手段[7-10]；因此，针对不同树种的受迫响应以及能量传递规律的研究尤为重要。

HE等[11]利用机械振动器对选取的甜樱桃树的枝条进行振动，在能量传递的过程中分析各响应区的动能变化。SOLA-GUIRADO等[12]通过测量橄榄树上多个点的加速度，分析不同高度对树体振动的影响。DU等[13]对甜樱桃树进行激振试验，研究发现距离激振点位置越远的树枝位移响应越大，能量传递效率与树体结构有关，横向分枝较少的树体从激励位置至末端的能量传递效率较高。李斌等[14]利用一种动-定梳排组合式采摘机构进行了荔枝采摘试验，对树枝的能量传递特性进行了研究。当作用位置接近位于树冠外侧位置上的侧枝时，传递至最末端树枝上的振动能量利用的效率更高。但其结果具有局限性，其他类型作用机构对树体的影响有待进一步研究。LNG等[15-16]建立了一种二自由度的果树模型分析樱桃树的动能响应。该模型的计算结果与实际测试结果吻合较好。刘晓雯等[17]为研究苹果振动采收最佳频率，基于伯努利梁建立了树枝动力学模型，采用有限元法得到不同激励下树枝的响应，发现枝条在振动下具有不相关性，频率越高，能量的传递效率越高。魏庭鹏等[18]将海棠树的树干与树枝的模型简化为两个自由度的质量刚度阻尼模型，并建立运动方程，通过Matlab对方程进行仿真，并通过试验验证，得到了使得果实下落的最佳振动频率为1.72、4.18、7.72 Hz，载荷的增加使得加速度响应幅值逐渐增加。

综上所述，学者们已经对一些果树进行能量传递特性的研究。但是在振动采摘过程中，不同种类树的能量传递特性存在较大差异。本文以油茶树为研究对象，建立树枝质量-弹簧-阻尼动力学模型；以不同激振参数作为输入，通过Matlab软件对运动方程进行仿真，分析油茶树各级枝间的能量传递规律，并确定油茶树冠层振动采摘油茶果的振动方法；利用Design-Expert 11.0.4 软件设计仿真试验，并对振动参数进行优化；通过田间试验对冠层振动采摘油茶果过程中油茶树能量传递规律进一步研究，并对仿真分析结果进行验证，通过采摘效果证明从能量传递角度优化振动参数方法的有效性。

1 油茶树枝动力学模型建立

果树的物理性质比较复杂,枝条是一个复杂的、连续的、非线性的柔性系统，系统运动的幅度与所受的外载荷成非线性关系[19]。现有研究表明利用质量-弹簧-阻尼模型研究树木的动力学特性比较符合实际[20]。利用线性模型对非线性的枝条进行离散表达，进而研究果树枝干的动力学特性。

1.1 质量-弹簧-阻尼模型建立

树木主要以单轴和合轴(Y型)的分枝方式生长，这与生长环境之间存在复杂的联系[21]。油茶树的分枝方式多数以合轴的方式生长，因此本文以Y型油茶树为研究对象，如图1a所示，图中1～16为加速度传感器的安装位置。建立包含1个主干、2个一级侧枝和2个二级侧枝的5自由度振动等效动力学模型，如图1b所示。

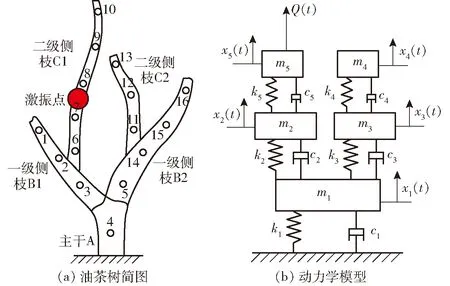
图1 油茶树枝动力学模型Fig.1 Dynamics models of Camellia oleifera

将油茶树的主干和各级分枝简化为质量块在弹簧和阻尼约束下的5自由度系统，油茶树枝在采摘装置作用下的运动被简化为等效模型在激振力Q(t)作用下的运动。令油茶树主干A、一级侧枝B1、B2、二级侧枝C1、C2离开平衡位置的位移分别为x1(t)、x2(t)、x3(t)、x4(t)、x5(t)。

当油茶树受迫振动时，对于主干A的响应可以视为一级侧枝B1、B2的作用效果；即两个质量分别为m2、m3，刚度分别为k2、k3和阻尼系数分别为c2、c3的系统对质量为m1、刚度为k1和阻尼系数为c1的作用。根据力的平衡条件并整理有

(1)

对于一级侧枝B1的响应可以视为二级侧枝C1和主干A的作用效果；即两个质量分别为m5、m1，刚度分别为k5、k1和阻尼系数分别为c5、c1的系统对质量为m2、刚度为k2和阻尼系数为c2的作用。根据力的平衡条件并整理有

(2)

对于一级侧枝B2的响应可以视为二级侧枝C2和主干A的作用效果；即两个质量分别为m4、m1，刚度分别为k4、k1和阻尼系数分别为c4、c1的系统对质量为m3、刚度为k3和阻尼系数为c3的作用。根据力的平衡条件并整理有

(3)

对于二级侧枝C2的响应可以视为一级侧枝B2的作用效果；即一个质量为m3，刚度为k3和阻尼系数为c3的系统对质量为m4、刚度为k4和阻尼系数为c4的作用。根据力的平衡条件并整理有

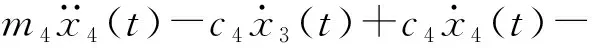
(4)

对于二级侧枝C1的响应可以视为一级侧枝B1和激振力Q(t)的作用效果；即一个质量为m2，刚度为k2和阻尼系数为c2与外部激振力Q(t)的系统对质量为m5、刚度为k5和阻尼系数为c5的作用。根据力的平衡条件并整理有

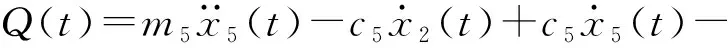
(5)

将油茶树主干以及各级枝受迫振动的运动学方程(1)～(5)整理，写成矩阵的形式为

(6)

其中

式中x——位移矩阵M——质量矩阵

F——作用力矩阵

C——阻尼系数矩阵K——刚度矩阵

1.2 动力学模型等效参数确定

阻尼比是一个与结构相关的物理量，并不代表材料性能参数[22]。然而，对于大多数材料，相似尺寸和结构的试件测得的阻尼比接近[23]。

在样本树上选取适当的位置布置加速度传感器，拉动棉绳使树枝产生一定的位移，随后迅速释放棉绳。利用KDDASP型仪器对动态信号进行采集，在样本树上重复进行3次试验，选取衰减曲线较为清晰的一组进行分析。各级枝衰减曲线如图2所示。

图2 各测点衰减曲线Fig.2 Attenuation curves of each measuring point

利用对数衰减法求出油茶树各级枝的阻尼比，计算式为

(7)

其中

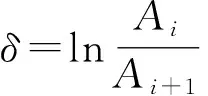
(8)

式中Ai——同方向相邻前一个振幅，mm

Ai+1——同方向相邻后一个振幅，mm

δ——对数衰减率

ξ——阻尼比

通过式(7)、(8)计算得出油茶树主干A，一级侧枝B1、B2和二级侧枝C1、C2的阻尼比分别为0.408 3、0.134 3、0.061 4、0.091 4、0.080 1。

通过试验测得的动态加速度信号，利用FRF频响函数分析得到激励力与主干、一级侧枝、二级侧枝之间的频响函数如图3所示，各级树枝上都存在较多的固有频率，本文只对频率35 Hz内的情况进行研究。

图3 油茶树各级枝频响函数Fig.3 Frequency response functions of all branches of Camellia oleifera

由图3可知，主干的前5阶固有频率分别是0.97、2.98、5.35、7.81、9.77 Hz。一级侧枝前5阶固有频率分别是0.97、2.98、8.79、12.7、14.65 Hz。二级侧枝前5阶固有频率分别是0.97、2.98、4.88、6.84、8.47 Hz。可以发现，果树上不同级别树枝的低阶固有频率有相同也有不同，从分析的结果来看，主干、一级侧枝、二级侧枝的相同固有频率为0.97、2.98 Hz。

油茶果冠层振动式采摘中，在树体的共振频率下作业，树枝的响应更为理想。作业时需要一级侧枝和二级侧枝产生共振来提高树枝上的振动能量，从而更有利于果实的脱落。在振动采摘过程中振动响应较大，所以在计算过程中选择固有频率为2.98 Hz。对选取的样本油茶树生物性状进行测量，获得油树枝的直径d和长度l平均值。

等效质量m为

(9)

式中ρ——油茶树密度，取950 kg/m3[24]

等效刚度k为

(10)

式中ω0——油茶树固有频率，取2.98 Hz

等效阻尼系数c为

(11)

利用本课题组研发制作的“树冠振动式油茶果采收机”作为激振装置，其工作原理是曲柄-连杆-滑块机构[25]。所以等效激振力F为

F=M0ω2rsin(ωt)

(12)

(13)

式中M0——激振装置质量，取5 kg

ω——角速度，rad/s

r——曲柄半径，mm

t——工作时间，sf——激振频率，Hz

对30个随机样本进行测量计算，得到油茶树等效模型所确定的各等效参数如表1所示。

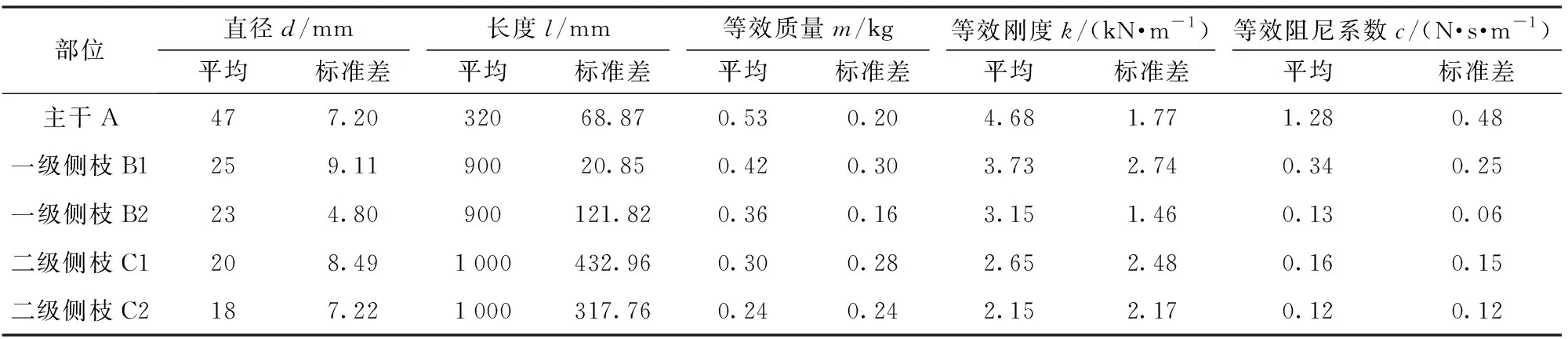
表1 油茶树等效参数Tab.1 Equivalent parameters of Camellia oleifera

2 仿真分析

利用动能衡量油茶树各级枝上的能量，对不同级树枝上动能进行测量计算，进而研究能量的变化规律。采用Matlab软件中的Simulink模块的子系统封装技术[26]，建立油茶果树等效模型的运动微分方程如图4所示。

图4 运动微分方程仿真框图Fig.4 Block diagrams of motion differential equation simulation

子控制系统与封装系统的通讯连接通过图中标注的数字实现，即相同数字相互连通。图中的1～10号端口分别为各子控制系统的输入端，11～20号端口分别为各子控制系统的输出端，0号端口为激振力的输入端。图4a～4e为油茶树主干及各级枝的质量弹簧阻尼模型的微分运动方程，图4f为系统封装图。

利用Subsystem模块分别建立5自由度油茶树质量-弹簧-阻尼系统的各子系统。包括油茶树主干A，一级侧枝B1、B2和二级侧枝C1、C2。将等效参数通过Gain模块带入到各子系统。在子系统中使用Integrator模块进行积分运算，将一次、二次积分所得的速度和位移输出到子系统外，输出的速度和位移作为输入通过Gain模块以及Adds模块根据动力学方程连接到相应的子系统中；对子系统输出的位移使用Derivative模块进行两次微分运算得到各子系统的加速度，通过Scope模块显示加速度的变化曲线，利用Math Function模块对子系统的速度进行平方运算，连接等效质量作为增益的Gain模块进行各模块的动能计算，将其都连接至一个Scope模块显示各级枝的动能变换曲线。通过To Workspace模块将数据输出到工作空间。将不同频率不同振幅下的等效力作为输入进行动力学仿真。

2.1 各级枝间能量传递规律

根据前期研究，选择采摘效果相对较好、能量传递规律明显的振动参数组合进行能量传递规律分析。以频率为5 Hz、振幅为60 mm时的等效激振力作为输入，仿真时间为5 s，得到各级枝条的动能变化曲线如图5所示。

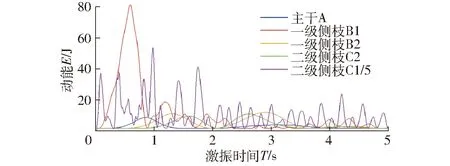
图5 油茶树各级枝的动能变化曲线Fig.5 Kinetic energy change of branches of Camellia oleifera branches

由图5可知，激振力所作用的二级侧枝C1的动能平均值最大，其次是一级侧枝B1，主干A的动能平均值最小。其原因可能是油茶树主干与根部相连接，振动趋势受大地的阻力作用较大。二级侧枝C1到一级侧枝B1的能量下降了52.65%，从一级侧枝B1到油茶树主干A的能量下降了74.33%，从一级侧枝B1传递到B2时能量下降26.02%，从一级侧枝B2传递到二级侧枝C2的能量下降45.49%，能量由二级侧枝C1传递到二级侧枝C2的过程中，能量损失80.9%。

通过对比油茶树主干以及各级侧枝达到动能峰值的时间可知，激振力所作用的二级侧枝C1首先达到动能峰值，其次是一级侧枝B1，随后是主干A，接着是一级侧枝B2，最后是二级侧枝C2；因此，从激振位置沿着传递路径，油茶树主干及各级枝的动能峰值出现的时间具有滞后性。

2.2 仿真试验

为了分析不同振动参数采用冠层振动方式对油茶树主干及各级枝能量传递特性的影响，选择油茶树二级侧枝C1的激振时间、激振频率和振幅为试验因素。由于能量传递过程中损失严重，为了在振动采摘过程中获得较高油茶果采收率，能量传递最后一级侧枝的能量尽可能多。因此，以油茶树主干以及各级枝的动能E为评价指标。利用Design-Expert 11.0.4软件进行试验方案设计，共进行17组，取振动过程中动能平均值作为试验结果。经过前期预试验以及课题组相关研究成果[27-28]，选定各试验因素编码如表2所示。

表2 试验因素编码Tab.2 Test factors and level coding

2.2.1仿真试验结果

仿真试验结果如表3所示，X、Y、Z为因素编码值。

表3 仿真试验设计方案与结果Tab.3 Simulation test design scheme and results

2.2.2方差分析与回归方程建立

利用Design-Expert 11.0.4软件对油茶树各枝动能的仿真试验结果进行方差分析，结果如表4所示。

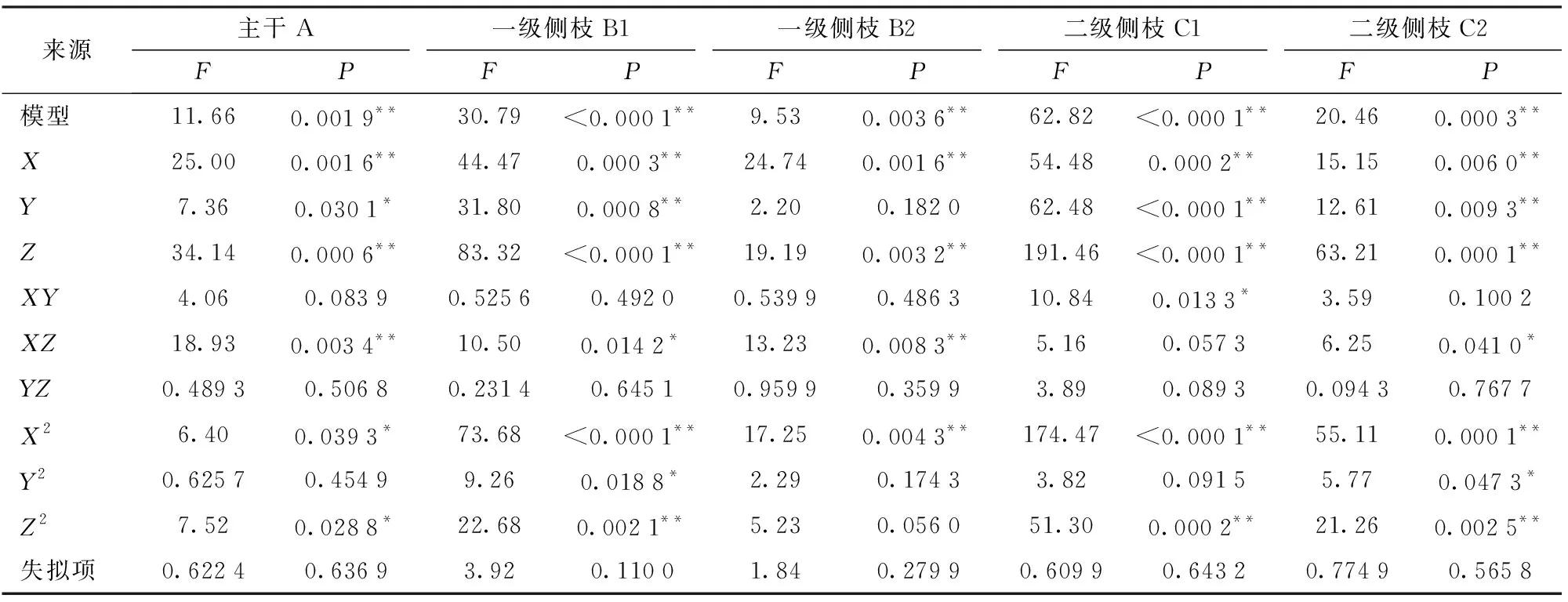
表4 仿真试验结果方差分析Tab.4 Analysis of variance of simulation test results

方差分析结果表明，油茶树主干A的多项式回归方程模型的P为0.001 9，小于0.01，说明回归模型极其显著；失拟项的P为0.636 9，大于0.05，说明回归模型比较稳定；模型决定系数R2为0.937 4，说明该模型可以反映93.74%的响应值变化；表明得到的多项式回归方程模型拟合程度较高，拟合效果较好。X、Z和XZ项对回归模型的影响极其显著；Y、X2和Z2项对回归模型的影响显著；XY、YZ和Y2项对回归模型的影响不显著。油茶树主干A与激振时间、激振频率、振幅之间的二次多项式回归方程为

EA=2.40-1.15X+0.62Y+1.34Z-0.66XY-
1.42XZ-0.23YZ+0.80X2-0.25Y2+0.87Z2

(14)

油茶树一级侧枝B1的多项式回归方程的P<0.000 1，小于0.01，说明回归模型极其显著；失拟项的P为0.110 0，大于0.05，说明回归模型比较稳定；模型决定系数R2为0.975 4，说明该模型可以反映97.54%的响应值变化；表明得到的多项式回归模型拟合程度较高，拟合效果较好。X、Y、Z、X2和Z2项对回归模型的影响极其显著；XZ和Y2项对回归模型的影响显著；XY和YZ项对回归模型的影响不显著。油茶树二级侧枝B1与激振时间、激振频率、振幅之间的二次多项式回归方程为

EB1=8.43-3.53X+2.98Y+4.83Z-0.54XY-
2.43XZ+0.36YZ+6.26X2-2.22Y2+3.47Z2

(15)

油茶树一级侧枝B2的多项式回归方程的P为0.003 6，小于0.01，说明回归模型极其显著；失拟项的P为0.279 9，大于0.05，说明回归模型比较稳定；模型决定系数R2为0.924 5，说明该模型可以反映92.45%的响应值变化；表明得到的多项式回归方程模型拟合程度较高，拟合效果较好。X、Z、XZ和X2项对回归模型的影响极其显著；Y、XY、YZ、Y2和Z2对回归模型的影响不显著。油茶树二级侧枝B2与激振时间、激振频率、振幅之间的二次多项式回归方程为

EB2=5.57-3.55X+1.06Y+3.13Z-0.74XY-
0.68XZ-0.99YZ+4.09X2-1.49Y2+2.25Z2

(16)

油茶树二级侧枝C1的多项式回归方程的P<0.000 1,小于0.01，说明回归模型极其显著；失拟项的P为0.643 2,大于0.05，说明回归模型比较稳定；模型决定系数R2为0.987 8，说明该模型可以反映98.78%的响应值变化；表明得到的多项式回归方程模型拟合程度较高，拟合效果较好。X、Y、Z、X2和Z2对回归模型的影响极其显著；XY项对回归模型的影响显著；XZ和YZ项对回归模型的影响不显著。油茶树二级侧枝C1与激振时间、激振频率、振幅之间的二次多项式回归方程为

EC1=14.61-3.73X+3.99Y+6.99Z+2.36XY-
1.63XZ+1.41YZ+9.21X2-1.36Y2+4.99Z2

(17)

油茶树二级侧枝C2的多项式回归方程的P为0.000 3，小于0.01，说明回归模型极其显著；失拟项的P为0.565 8，大于0.05，说明回归模型比较稳定；模型决定系数R2为0.963 4，说明该模型可以反映96.34%的响应值变化；表明得到的多项式回归方程模型拟合程度较高，拟合效果较好。X、Y、Z、XZ、X2、Y2和Z2对回归模型的影响极其显著；XY和YZ项对回归模型的影响不显著。油茶树二级侧枝C2与激振时间、激振频率、振幅之间的二次多项式回归方程为

EC2=2.41-0.94X+0.86Y+1.92Z+0.65XY-
0.86XZ+0.11YZ+2.47X2-0.80Y2+1.54Z2

(18)

2.2.3响应面分析

根据方差分析可知，激振时间和振幅之间的交互作用对油茶树主干A，一级侧枝B1、B2和二级侧枝C2的能量变化是显著的，激振时间和激振频率之间的交互作用对油茶树二级侧枝C1的能量变化是显著的，因此利用响应面分析法对交互作用显著项进行分析，固定一个试验因素处于零水平，研究其余两个因素之间的交互作用响应，响应曲面如图6所示。

图6 各因素交互作用影响多油茶树枝动能的响应曲面Fig.6 Response surfaces of tree kinetic energy of Camellia oleifera under interaction of various factors

当激振频率为7 Hz时，激振时间和振幅的交互作用对油茶树主干A、一级侧枝B1、B2和二级侧枝C2动能的响应曲面如图6a～6c、6e所示。油茶树主干A的动能与激振时间呈负相关，与振幅呈正相关趋势；一级侧枝B1的动能与振幅呈正相关，随着激振时间的增大呈先降低后升高的趋势；当激振时间为5～10 s时，一级侧枝B2的动能与振幅呈正相关，当激振时间为10～15 s时，一级侧枝B2和二级侧枝C2的动能随着振幅的增大呈先降低后升高的趋势；当振幅为50～60 mm时，一级侧枝B2的动能随着激振时间的增大呈先降低后升高的趋势，当振幅为60～70 mm时，一级侧枝B2的动能与激振时间呈负相关；当振幅为60 mm时，激振时间和激振频率的交互作用对油茶树二级侧枝C1动能的响应曲面如图6d所示。油茶树二级侧枝C1的动能与激振频率呈正相关，随激振频率的增大而增加，随着激振时间的增加呈先降低后增加的趋势。油茶树各级枝的平均动能随着激振时间的延长而减小，随着振幅的增大而增大，与激振频率的变化动能响应不明显。

2.2.4参数优化

根据上述试验结果分析，不同的振动参数对油茶树的能量传递规律具有较大的影响，为获得冠层振动采摘油茶果的最优工作参数，利用Design-Expert 11.0.4软件的优化模块进行优化求解。由于油茶树各级枝间的能量传递损失严重，所以对一棵油茶树进行2～3次振动采摘的效果最佳。油茶树主干上基本没有油茶果，所以设置优化目标函数为油茶树一级侧枝B1、二级侧枝C1动能最大，主干A的动能最小。又二级侧枝油茶果实略多于一级侧枝，故设定二级侧枝C1的权重为0.5，一级侧枝B1的权重为0.4，油茶树主干A的权重为0.1。设置目标函数为

(19)

对目标函数优化求解得到油茶果冠层振动采摘的最优工作参数组合为：振动时间7.14 s、振动频率7.18 Hz、振幅52.41 mm，在此参数组合下油茶树主干A的动能为2.95 J；一级侧枝B1、B2的动能分别为15.09、9.64 J；二级侧枝C1、C2的动能分别为23.93、4.61 J。

3 田间试验

为了进一步研究油茶树在机械采摘过程中的动态响应情况以及验证等效模型和仿真分析的准确性，利用本课题组研发制造的“树冠振动式油茶果采收机”进行油茶果采摘试验(图7)，通过KDDASP动态信号采集系统进行田间数据采集，同时记录油茶果实与花苞脱落情况。

图7 田间试验Fig.7 Field experiment

对油茶树按照图1a所示的测量点布置加速度传感器，测量点相距200 mm左右。由于激振装置的控制精度有限，对优化的激振参数结果进行处理，取激振时间7 s、激振频率7 Hz和振幅50 mm。设置激振参数对结构相似的油茶树进行3次试验，取平均值作为最后结果。

3.1 同枝条内能量传递规律

为了研究油茶树各级枝条内部的能量传递规律，在最佳振动参数作用下，选择一级侧枝B2为研究对象，其上的测点分别为5、14、15、16。将采集的数据导入Matlab中进行数据处理，以微元段的动能来进行分析，截取的各测点动能峰值所在段曲线如图8所示。

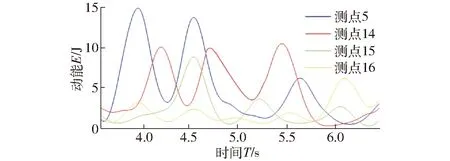
图8 一级侧枝B2上测点5、14、15、16动能曲线Fig.8 Kinetic energy curves of points 5, 14, 15 and 16 on the first branch B2

由图8可知，从测点5到测点14能量峰值减小了34%，从测点14到测点15能量峰值减小了20%，从测点15到测点16能量峰值减小了23%。能量沿着树枝传递时，动能与传递距离成反比，传递的距离越远能量越小；且越靠近激振位置，能量峰值出现的时间越短。

3.2 各级枝间能量传递规律与落果率

利用Matlab中的数据处理软件对动态信号采集系统采集的试验数据进行处理，最终取油茶树各级枝上所有测点测量值的平均值作为该级枝的动能。田间试验结果如表5所示。

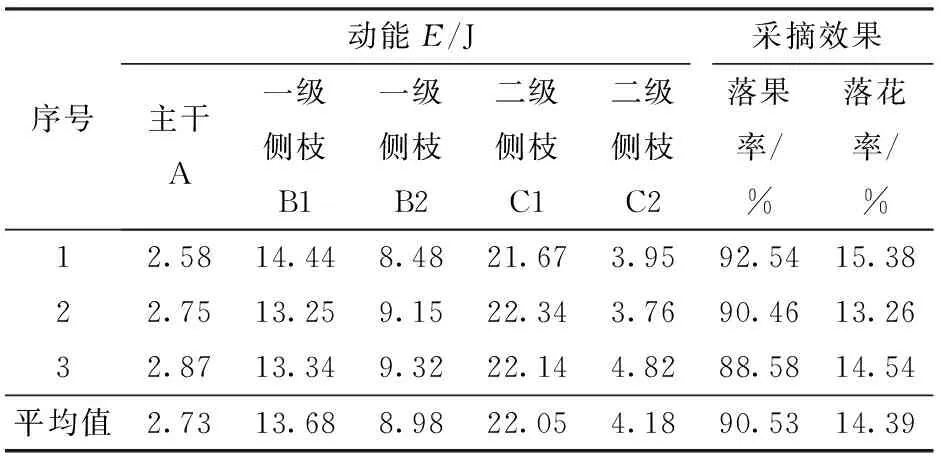
表5 田间试验结果Tab.5 Field test results

田间试验结果表明，能量传递规律与仿真结果相同，油茶树枝条内部的能量传递规律与各级枝之间的能量传递规律保持一致，即越靠近激振位置，能量峰值出现的时间越短。油茶树主干A、一级侧枝B1、B2和二级侧枝C1、C2动能的平均值分别为2.73、13.68、8.98、22.05、4.18 J，与仿真结果的相对误差分别为7.34%、9.37%、6.81%、7.86%和9.39%。油茶果脱落率平均值为90.53%，花苞脱落率平均值为14.39%，采摘效果较好，说明此参数组合满足机械化收获要求。

田间试验时，油茶树各级枝的动能明显低于仿真结果，其可能的原因为：优化后的参数组合经过修改，会对试验结果造成一定误差；通过振动等效模型得到的能量传递的结果是理想状态下的，而田间的情况相当复杂，树体的长势、形状、枝叶的浓密程度将影响试验结果。但是田间试验和仿真结果的相对误差均在10%之内，说明优化后的振动参数具有较好的可靠性，表明此振动等效模型具有较高的准确性。

4 结论

(1)建立了5自由度油茶树的质量-弹性-阻尼动力学模型，包括1个主干，2个一级侧枝和2个二级侧枝；通过绳拉试验使树枝自由衰减的方法测量油茶树主干A、一级侧枝B1、B2和二级侧枝C1、C2的阻尼比分别为0.408 3、0.134 3、0.061 4、0.091 4、0.080 1，进而得到了仿真试验所需的等效参数。

(2)运用Matlab软件中的Simulink组件建立微分运动方程的仿真框图，将不同的振动时间、频率和振幅下的作用力作为仿真的输入进行仿真分析。结果表明，能量由二级侧枝C1传递到C2的过程中损失80.9%。从输入位置沿着传递路径，各级枝的动能峰值出现的时间具有滞后性。

(3)利用Design-Expert 11.0.4软件设计二次旋转正交组合试验，仿真试验结果表明，不同激振参数对油茶树能量传递特性的影响较大。建立各因素与指标之间的回归模型并进行方差和响应面分析；根据油茶树各级枝间的能量传递损失严重，完成一棵树的油茶果采摘将进行2～3次振动，并对激振参数进行优化求解，得到最佳振动参数组合为振动时间7.14 s、振动频率7.18 Hz、振幅52.41 mm。

(4)田间试验结果表明，油茶树各级枝间以及各级枝条内部的能量传递规律相同。能量沿着树枝传递时，动能与传递距离成反比，传递的距离越远能量越小；且越靠近激振位置，能量峰值出现的时间越短。通过验证，田间试验结果与仿真结果的相对误差在10%以内，说明该动力学模型具有较高的可靠性；振动采摘部分油茶果实和花苞平均脱落率分别为90.53%、14.39%，采摘效果较好，证明了从能量传递角度优化振动参数方法的有效性。