大口径平面镜快速瑞奇-康芒测量法研究

刘 昕，王 聪，刘永强，袁 阳，陈晓磊，张 瑜，韩娟妮，张超凡

（西安应用光学研究所，陕西 西安 710065）

引言

光学平面镜是光学系统中重要的一类零件。大口径光学平面的检测需要用同等或更大口径的激光干涉仪进行检测，而大口径干涉仪价格昂贵，震动、温度波动和气流对测量精度影响大[1]，测量面形时需要远离生产现场震源并保持恒温，只能用于最终检测，因而寻找低成本、快速高效的检测手段是大口径平面镜制造阶段的现实需要。

为解决大口径平面镜检测，出现了五棱镜扫描、子孔径拼接、斜入射法、瑞奇-康芒法等多种方法。五棱镜扫描法使用五棱镜扫描平面镜表面，分析入射光束与出射光束间夹角表征的该点倾斜程度，反演出面形[2-3]；子孔径拼接法将被测件表面划分为多个相互重叠的子孔径，分别检测子孔径内的面形后进行拼接，得到整个表面的面形，可应用于平面、球面、非球面等多种面形检测[4-5]。五棱镜扫描法和子孔径拼接法均为局部拼合成整体的方法，单次测量耗时长，测量精度依赖于移动过程的机械定位精度，拼接算法的质量对检测精度影响很大。斜入射法将平行平板以某一角度插入平面干涉仪与平面参考镜构成的光路中，根据偏转角度的不同而获得偏转方向的检测尺寸扩展，而垂直于该方向的尺寸无放大作用，适用于短轴小于干涉仪口径的矩形或椭圆形平面检测[6-7]。瑞奇-康芒法用平面镜折转球面检测光路，由于球面波的扩束作用，其检测口径仅受限于球面参考镜的口径，使用小口径的球面激光干涉仪即可检测大口径圆形及其他形状的平面镜，是低成本检测大口径的理想手段，但其单次检测中需要使用2 种瑞奇角及被测镜多次自转进行重复测量，以分离调试产生的离焦量和像散，影响了测试的效率和精度[8-9]。

为了满足大口径平面镜加工过程中的低成本高效测量需求，本文研究了瑞奇-康芒法各参量对测量精度的影响，提出了快速瑞奇-康芒检测法，仿真分析该方法中各调整参量误差对测量误差的影响，对比该方法检测与干涉仪直接测量的结果，证明了该方法的有效性。

1 瑞奇-康芒法测量原理

1.1 基本原理

如图1 所示，从激光干涉仪发出的球面波，经过与干涉仪光轴成90°-θ角的被测平面镜反射后投射到球面参考镜上，球面参考镜球心与检测光束焦点重合时，反射后的检测光束再次被平面镜反射原路返回，与干涉仪标准球面镜头的参考光束发生干涉。干涉仪检测并分析干涉波像差，得到包含干涉仪标准镜头、球面参考镜和被测平面镜的综合误差，由于标准镜头和球面参考镜面形精度远高于被测平面镜精度要求，因此认为检测波像差只与平面镜面形误差有对应关系。其中，θ角称为瑞奇角。

图 1 瑞奇-康芒法检测光路图Fig.1 Optical path diagram of Ritchey-Common test

反射镜法线与光轴存在夹角θ，测得的干涉图是一个近似椭圆，需要对波像差进行复原，得到平面镜表面误差。复原方法有影响函数矩阵法[10]和坐标转化法[11]。

影响函数矩阵法是用Zernike 多项式表示系统波像差，将光瞳面的弧矢面坐标近似为被测平面镜的弧矢面坐标，推导出影响函数矩阵，根据波像差多项式系数和影响函数矩阵计算得到被测平面镜面形的Zernike 多项式系数，进而以最小二乘法拟合出被测表面的面形误差。影响函数矩阵法中弧矢面坐标和推导矩阵有2 次近似计算，且Zernike多项式相对于波像差舍弃了残余误差，得到的平面镜面形存在较大误差。

坐标转换法是将光瞳面坐标(Xp,Yp)按照几何关系转换为被测平面镜表面坐标(Xs,Ys)，计算检测光束在平面镜表面各点的入射角I(Xs,Ys)，根据光线传播关系得到平面镜面形误差。光瞳面坐标与被测平面镜表面坐标关系如图2 所示。

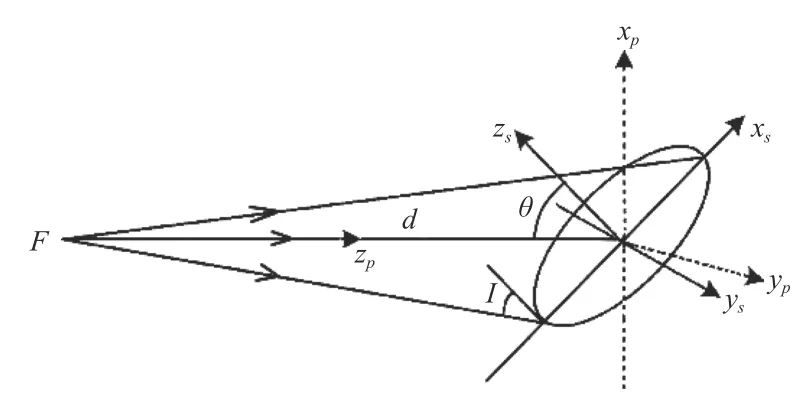
图 2 坐标转换示意图Fig.2 Schematic diagram of coordinate conversion

根据几何关系，有如下转换公式：

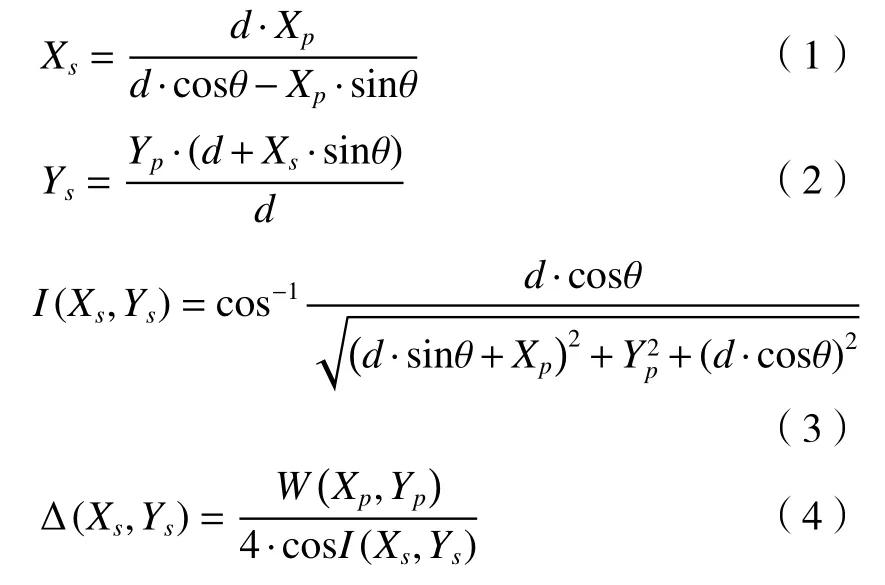
式中：Xp、Yp表示光瞳面坐标；Xs、Ys表示被测平面镜表面坐标；d为检测光束焦点到光轴与平面镜的交点距离；θ为瑞奇角；I(Xs,Ys)为检测光束在平面镜表面的入射角；Δ(Xs,Ys)表示平面镜表面误差；W(Xp,Yp)为系统波像差。

坐标转换法中，波像差W(Xp,Yp)和被测平面表面各点误差Δ(Xs,Ys)有明确的对应关系，据此可一一对应恢复被测平面镜表面误差，没有近似误差和拟合残余误差影响，复原精度优于影响函数矩阵法。

1.2 瑞奇-康芒法检测各参量对测量的影响

瑞奇-康芒法检测中球面参考镜半径、平面镜位置和瑞奇角等参量的设置会影响到波像差，瑞奇角的误差则会影响到波面复原的精度。本节中将用Zemax 软件仿真平面镜位置误差在不同测量参量下引起的测量结果变化，评估设计瑞奇-康芒检测系统时各参量的选择原则。仿真光路中，光源在平面镜插入位置处光斑口径为242 mm，平面镜口径200 mm，球面镜口径360 mm，瑞奇角45°，在平面镜插入位置上附加位置误差，观察波像差的变化。

1）球面镜半径的影响

仿真参数设定：球面参考镜半径为1 122 mm、2 244 mm 和4 488 mm，对应的平面参考镜插入位置分别为距光源焦点800 mm、1 600 mm、3 200 mm。

对比不同设置的波像差可以发现，参考镜半径不同，相同的位置误差将使波像差的离焦量出现不同的改变。离焦量变化量如图3 所示。

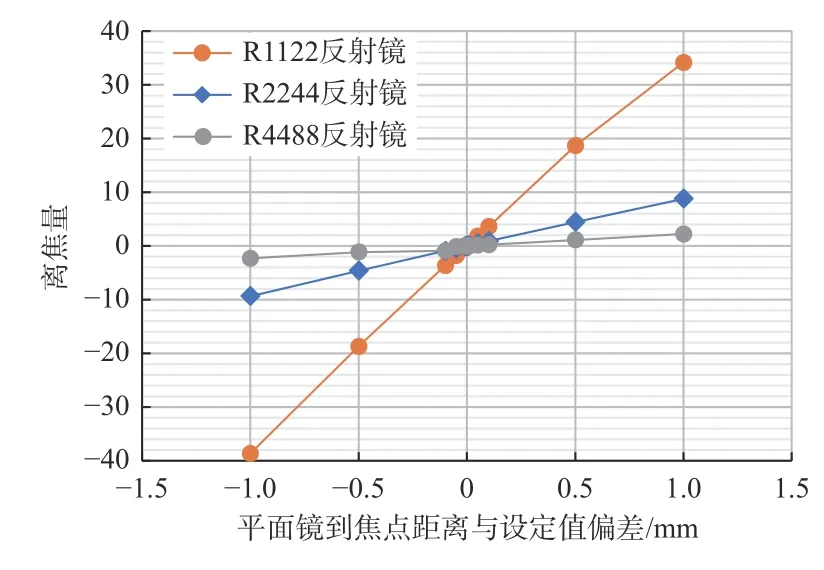
图 3 离焦量与球面镜半径的关系Fig.3 Relationship between defocus and radius of spherical mirror

观察离焦量变化，可得出结论：当FA位置存在误差时，球面镜半径越大，波像差的离焦量越小，变化量与球面参考镜半径之比的平方成反比；FA误差小于1 mm 时，离焦量近似成线性变化。

2）平面镜插入位置的影响

仿真参数设定：球面参考镜半径为1 122 mm，平面镜插入位置分别为距焦点700 mm、800 mm和900 mm。波像差离焦量变化如图4 所示。

平面镜位置误差在1 mm 以内时，离焦量近似成线性变化，且平面镜离焦点越远(越靠近球面参考镜)，平面镜位置误差引起的离焦量变化越小。

3）瑞奇角误差的影响

仿真表明，不同瑞奇角下平面镜位置误差引入的离焦量是相同的。

瑞奇角有2 种测量方法：测量焦点F、光轴与平面镜交点A与球面参考镜交点B三点间的距离，由余弦公式计算瑞奇角；运用图像处理技术中的边缘检测法分析波像差图像长短轴像素数比，用(1)式～(2)式反推出瑞奇角。实践中，要精确测量FA、AB、FB距离是困难的，边缘检测算法因为干涉图对比度低、干涉边缘条纹变形和干涉掩码等因素较难获得准确的瑞奇角，因此需要评估瑞奇角误差对波面复原精度的影响。

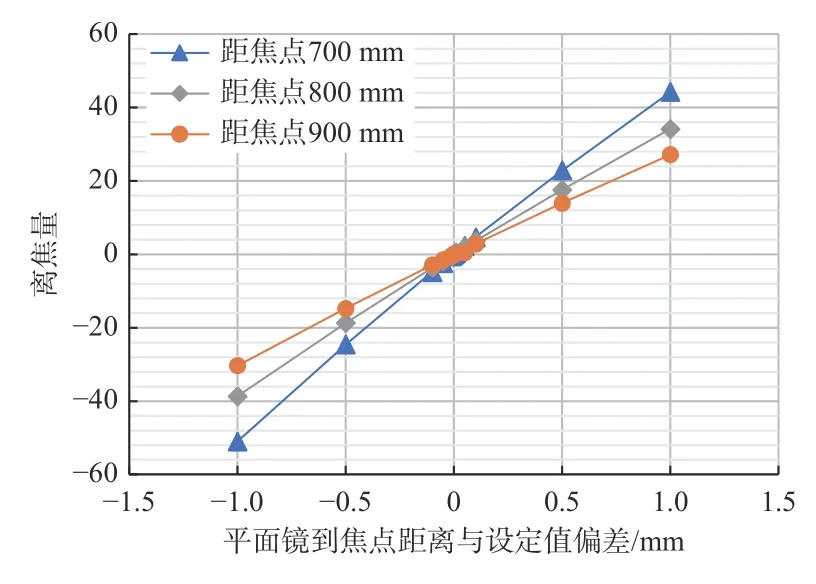
图 4 离焦量与平面镜插入位置的关系Fig.4 Relationship between defocus and position of flat mirror

选取瑞奇角为30°和45°、RMS 分别小于λ/25（λ=0.632 8 μm，下同）和λ/120 的4 种波像差图像，如图5 所示。在瑞奇角分别附加角度误差后按(1)式～(4)式进行波面复原，比较不同角度误差下复原波面的PV 和RMS。

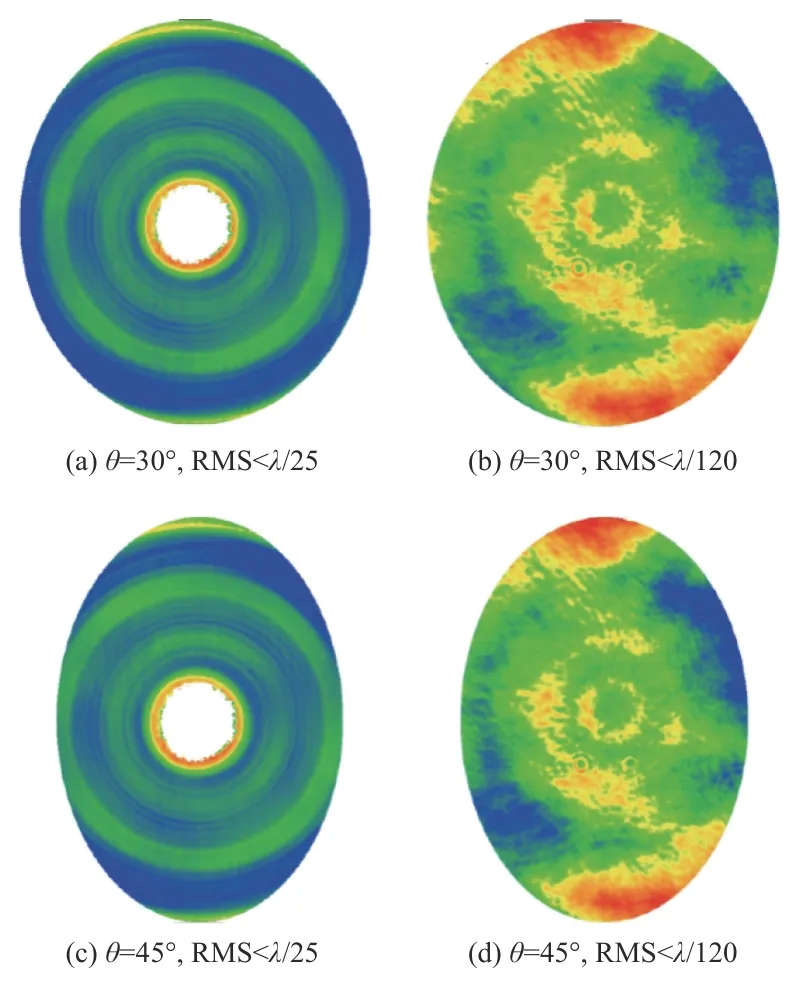
图 5 测试用波像差Fig.5 Wavefront aberration for test

波面复原结果如表1 所示。当瑞奇角误差大于1°时，目视即可观察到复原图轮廓与零件轮廓不一致；误差不大于1°时，随着瑞奇角的增大，复原后的PV 和RMS 均会增大，PV 最大变化为0.005 5 μm，RMS 为0.000 5 μm，对比干涉仪镜头PV≤0.031 64 μm的精度，瑞奇角误差对波面复原精度影响不大。

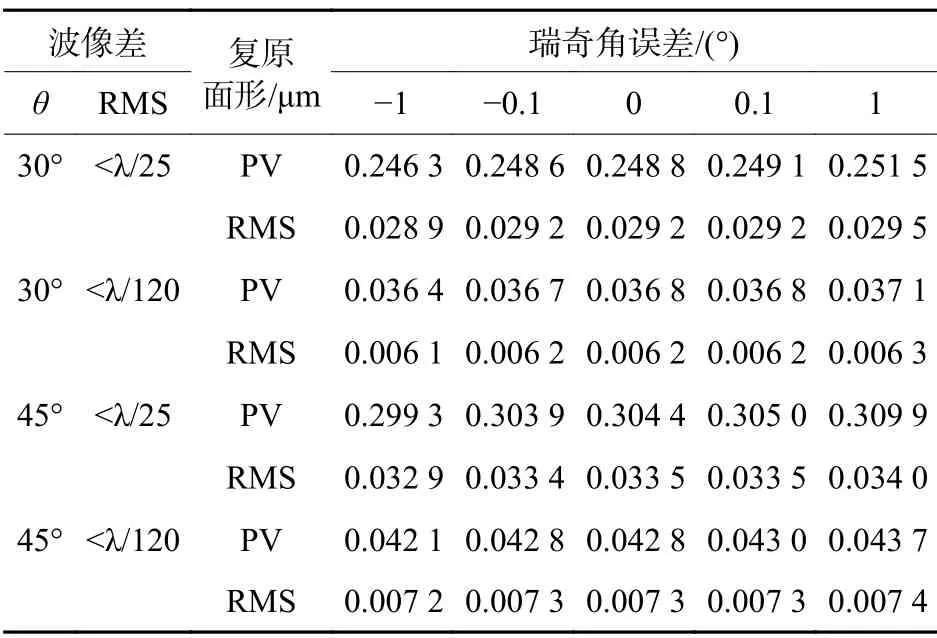
表 1 瑞奇角误差下对波面复原λTable 1 Wavefront restoration under condition of Ritchey angle error

瑞奇角大于50°时，平面镜波面复原后的测量误差逐渐增大，瑞奇角偏小时，球面参考镜边缘会遮挡干涉仪到平面镜的光束，因此瑞奇角一般设为20°～50°[12]。

根据仿真结果可知，用瑞奇-康芒法测量平面镜面形时，球面参考镜和平面镜的位置误差均会产生离焦量，而较大的球面参考镜半径和靠近球面参考镜的平面镜插入位置能够降低位置误差对波像差结果的影响；位置误差在不同的瑞奇角下产生的离焦量相同，波面复原时瑞奇角的误差对最终精度影响很小。

2 快速瑞奇-康芒测量法

瑞奇-康芒法测量时，波像差中包含了平面镜、球面镜的位置和两者与光轴的垂直度误差所引入的离焦量和像散[13]，以及平面镜加工产生的离焦量和像散，需要将测量误差和平面面形误差分离才能确定平面镜面形精度。误差分离方法有两角法[14]和平面镜自转法[15]。两角法是分别使用2 种瑞奇角测量平面镜以分离离焦量，而调整瑞奇角过程中有引入新调整误差的可能；平面镜自转法则需要多次绕自身轴旋转平面镜来分离像散误差。2 种方法均只能分离1 种误差，且要多次调整重复测量，测量过程复杂，效率低，随着被检平面镜口径的增加，测量难度和耗时显著增加。为解决大口径平面镜加工过程中的测量问题，本文提出一种快速瑞奇-康芒测量法。

2.1 快速瑞奇-康芒测量法

1）选择适当的球面参考镜半径和瑞奇角搭建瑞奇-康芒检测光路，用已知面形误差的校准平面镜插入光路。校准平面镜面形误差可用两角法和自转法测量。

2）调整光路至测量的波像差复原后与校准平面镜面形一致，用工装定位校准平面镜表面的空间位置。

3）取下校准平面镜，将被测平面镜固定至定位工装，测量后复原波面。

该测量方法用已知面形误差的平面镜消除测量光路调整过程中球面参考镜、平面镜的空间位置和角度误差，校准后可多次测量平面镜，耗时短，效率高。

2.2 快速瑞奇-康芒测量法误差分析

该方法中，被测平面镜固定到定位工装的定位误差将会引入测量误差，定位误差包括FA距离、AB距离、沿Zs轴的位移、绕Xs轴的旋转、绕Ys轴的旋转等。下面用Zemax 软件仿真平面镜位置偏移和角度旋转产生的误差。

瑞奇-康芒测量光路设置如图6 所示。

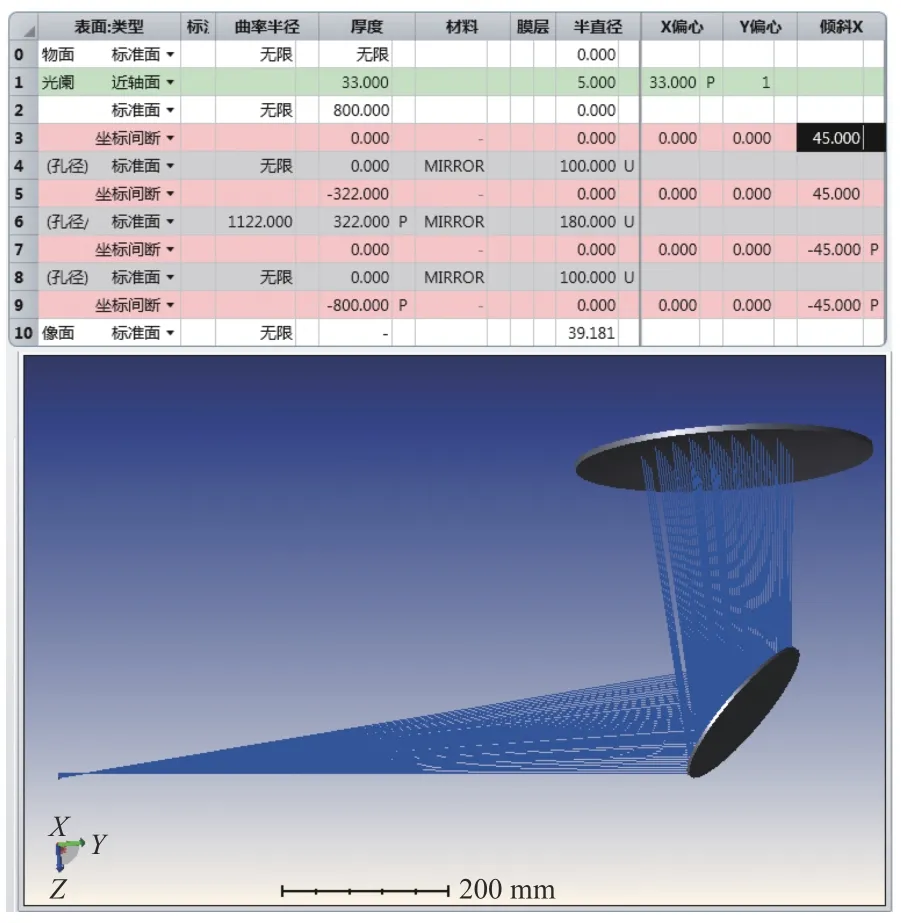
图 6 仿真参数设置Fig.6 Simulation parameters setting

1）平面镜位置偏移

在仿真光路的平面镜位置设置FA位置偏移，其余参数不变，仿真波像差中离焦量出现变化，变化量如表2 所示。

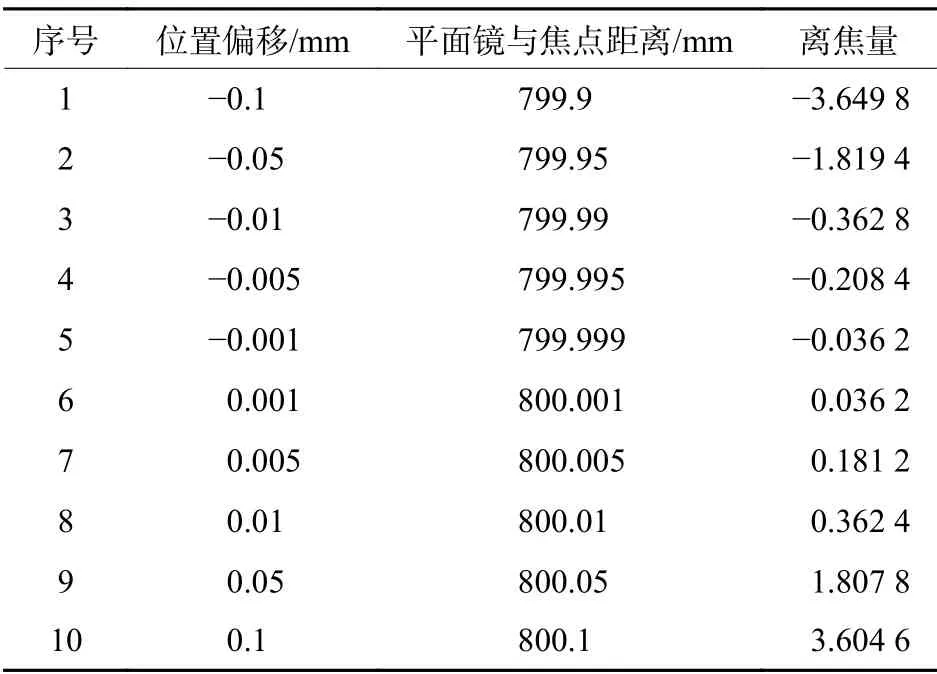
表 2 离焦量随FA 长度的变化Table 2 Variation of defocus with FA length

同理可得，平面镜沿光轴远离球面参考镜时，离焦量变化与沿光轴远离焦点相同；平面镜沿Zs轴远离焦点和球面参考镜时，离焦量变化为沿光轴同等偏差时的倍。

2）平面镜绕Xs和Ys轴的旋转

当平面镜与校准平面镜位置存在Xs或Ys轴的旋转角度时，波像差存在离焦和像散2 种误差，见表3～表4。

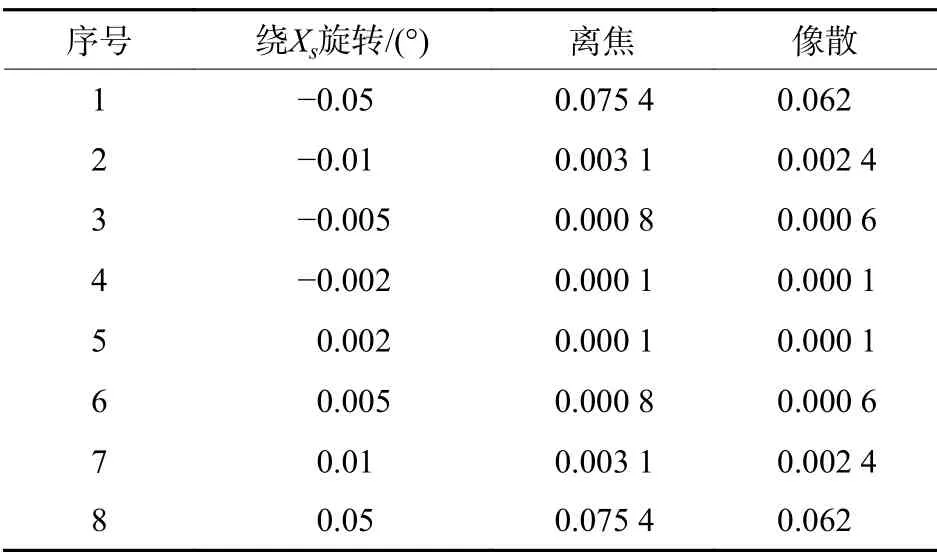
表 3 离焦量和像散随Xs 轴角度的变化Table 3 Variation of defocus and astigmatism with Xs-axis angle

3）平面镜定位精度引入的误差

由仿真可以看出，平面镜的0.001 mm 的位置偏移引入的离焦量为0.036 2，绕Xs和Ys轴的角度偏差引入的离焦量比位置偏移的变化要小得多，但会增加少量像散。

旋转和位置偏差均会引起自准后的光斑偏离干涉仪参考光斑，当偏差较大时，目视即可观察到光斑偏离，有利于发现定位误差。

3 实验

平面镜在Xs或Ys轴最大定位误差为0.001 mm造成的角度偏差约为0.000 3°，由此引入的离焦量和像散等测量误差远小于平面镜位置偏移0.001 mm引入的离焦误差。在设计、调试定位工装时，保证被测平面镜表面与校准平面镜表面的位置偏移严格一致是非常重要的。

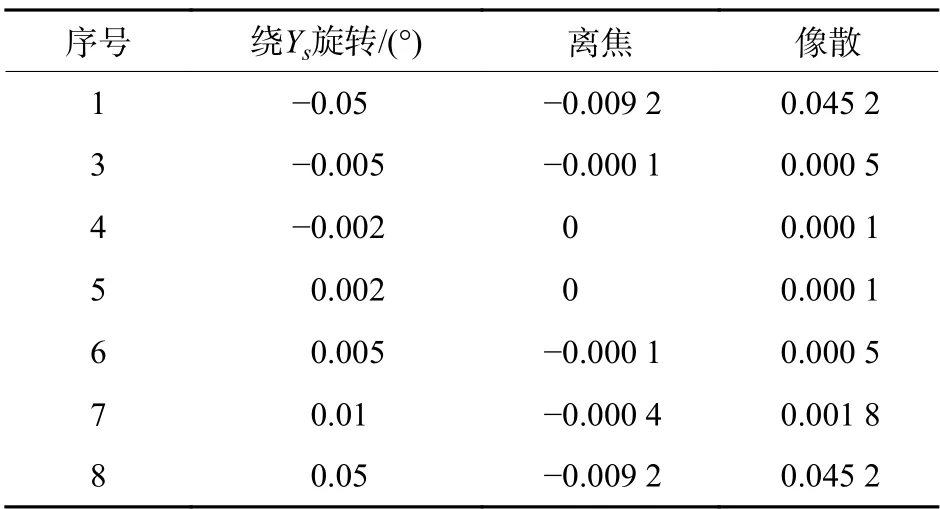
表 4 离焦量和像散随Ys 轴角度的变化Table 4 Variation of defocus and astigmatism with Ys-axis angle

为了验证快速瑞奇-康芒测量法的有效性，我们搭建了快速瑞奇-康芒法测量实验装置。实验装置中，球面参考镜半径1 122 mm，口径320 mm，激光干涉仪口径100 mm，搭配F3.3 镜头，瑞奇角设定为45°。将一块高精度校准平面镜，以表面定位固定到高精度3 点定位工装，在距干涉仪镜头焦点940 mm 处以45°角插入光路。调整球面参考镜、校准平面镜空间位置，使干涉波像差中像散、离焦小于0.01。保持实验装置和定位工装空间位置不动，取下校准平面镜，换上口径150 mm 被测平面镜，测量波像差。重复安装被测平面镜，以获得多组波像差。采用坐标转换法复原测得波像差的波面，比较复原波面和被测平面镜的Zygo 直测波面的PV 和RMS 值，如图7 所示。

图 7 直测面形、波像差和复原面形Fig.7 Direct measuring surface,Wave aberration and Restored surface

表5 列出5 次独立测量得到的复原面形。复原面形与直测面形之间，PV 最大差值0.015 1 μm，RMS 最大差值为0.003 6 μm；多组取平均值后PV 差值0.004 2 μm，RMS 差值为0.001 8 μm。

表 5 复原面形Table 5 Restored surfaceμm

实验中，复原面形与直测面形（PV=0.117 7 μm，RMS=0.013 9 μm)之间，最大差值小于干涉仪镜头的精度（PV=0.031 64 μm）。在校准后光路中测量平面镜面形时，仅需简单拆装后单次测量即可获得准确的面形，省去了多角度测量以分离离焦和像散的步骤，测量耗时显著减少。多角度测量以分离离焦和像散的步骤，测量耗时显著减少。

4 结论

瑞奇-康芒测量法需要多角度测量以分离离焦和像散，在测量大口径平面镜时效率低下。为了寻找适用于加工过程的高效平面镜面形测量法，通过仿真分析球面参考镜半径、平面镜插入位置和瑞奇角对测量精度的影响，证明较大的球面参考镜半径、远离干涉仪镜头焦点的插入位置能够改善测量精度，瑞奇角的测量误差对测量精度的影响不显著；据此提出了快速瑞奇-康芒测量法，仿真分析该方法下平面镜位置和角度误差对测量精度的影响，在测量实验中对比测量复原面形和直测面形，两者间最大差值PV=0.015 1 μm，RMS=0.003 6 μm，优于干涉仪镜头精度，证明了该方法的有效性。