基于自适应模糊神经网络的感应电机矢量控制
金爱娟,邵飞旋,严紫光
(上海理工大学 光电信息与计算机工程学院,上海 200093)
感应电机具有较低的成本和较高的可靠性,因而被广泛应用于工业生产与日常生活中。为降低硬件复杂性,减少成本,提高系统可靠性,针对感应电机无速度传感器矢量控制的研究一直都是领域内的热点[1-5]。在对转速估计精度和稳定性有要求的系统中,目前较为主流的感应电机转速闭环观测器方法包括:模型参考自适应法(Model Reference Adaptive System,MRAS)、全阶速度自适应观测器法(Adaptive Full-Observer,AFO)、扩展卡尔曼滤波器法(Extend Kalman Filter,EKF)、滑模观测器法(Sliding Mode Observer,SMO)和智能算法等[6]。MRAS通常将感应电机的电压模型设计为参考模型,将电流模型设计为可调模型。此方法原理简单也易于实现,但电压模型中存在纯积分环节,磁链模型会受到积分初值及零漂的影响,导致转速估计结果不准确,低速时性能较差[7]。EKF算法对电机转速辨识效果良好,算法的统计本质使得感应电机模型的非线性和不确定性对EKF的不利影响较小,但是EKF计算量巨大,不适用于高实时性驱动系统[8-9]。SMO不受参数变化和其他干扰的影响,但是其滑模控制的连续切换特性会带来抖动问题,从而影响控制精度[10-11]。智能算法近年来得到了蓬勃发展,转速辨识效果明显,但其目前的可行性一般。AFO是MRAS的一种特殊形式,其在状态估测方程中加入了校正环节,从而利用观测器的输出误差修正模型输入。因此,AFO具备较高的转速估计稳态精度。此外,该算法简单且易于实现,还有良好的抗干扰能力,得到了研究人员的广泛关注[12-13]。
随着智能算法的发展与微处理器算力的提高,越来越多的算法被应用于电机控制中。文献[14]利用水循环算法训练神经网络,自整控PI参数,优化了开关磁阻电机控制系统的动态性能。文献[15]提出了一种改进粒子群优BP神经网络PID的控制算法,用于调节矿井提升机的转速和转矩。文献[16]将模糊控制应用于混合励磁同步电机的励磁电流弱磁控制中,获得了良好的动态响应和抗干扰能力。ANFIS(Adaptive Neuro-Fuzzy Inference System)结合了模糊逻辑和神经网络,可在单个框架中兼具模糊的可推理性和神经网络的自学习优势[17-19]。本文在感应电机转速控制上引入了ANFIS。将ANFIS应用于感应电机的矢量控制系统中,使用来自PI控制器的数据对ANFIS进行训练,自动获得最佳控制系统模糊逻辑规则库、隶属函数和输出函数系数。通过将电机输出电流的实际值和观测器输出的电流估计值之间的误差组合得到误差项,然后结合自适应律得到估计转速。电机转速控制则通过经训练后的ANFIS方法得到。
1 感应电机矢量控制与数学模型
感应电机的矢量控制又被称为磁场定向(Field Oriented Control, FOC),其核心思想是借助坐标变换,对感应电机数学模型进行转化,将其等效为直流电机的数学模型,从而实现对磁通和转矩的解耦控制,获得可以类比直流电机的动态性能。本文采用基于转子磁链定向矢量控制策略,其结构如图1所示。

图1 矢量控制Figure 1. Vector control

假设感应电机的定子电流为状态变量,转子磁链为待观测变量,那么在静止坐标系下的数学模型如式(1)~式(4)所示。
(1)
(2)
ψs=Lsis+Lmir
(3)
ψr=Lmis+Lrir
(4)
将式(4)分别代入式(2)和式(3),消去ir,得
(5)
(6)
对式(6)两边取微分,得式(7)
(7)
将式(1)代入式(7)和式(5)中,得
(8)
式中,T′sr=L′s/Rsr;Rsr=Rs+(Lm/Lr)2Rr;L′s=σLs;Tr为转子时间常数,Tr=Lr/Rr;σ为漏磁系数,σ=1-Lm/(LsLr);Rs和Rr分别为定子、转子电阻;Ls和Lr和Lm分别为定、转子的自感和互感;ωr为转子角速度。
2 全阶自适应观测器
2.1 全阶自适应观测器原理
全阶自适应观测器利用感应电机数学模型构造可调模型,在自适应机构中获得估计转速。因此将式(5)和式(8)作为状态观测器的电机模型,将其写成矩阵形式

(9)
其中
(10)
式中,A为状态矩阵,且与转子速度ωr有关;I和0分别为2×2阶单位矩阵和零矩阵。则输出方程定义为式(11)。
(11)
为了构建全阶状态观测器,可以利用定子电流的观测误差来构成校正项,全阶状态观测器为
(12)
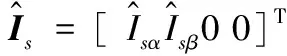
为确保观测器的快速收敛与稳定性,观测器的极点与感应电机的极点成正比例关系。假设大于1的比例系数为k,则Po=kPM,其中Po为观测器极点,PM为电机极点,给出G矩阵的表达式如式(13)所示。
(13)
2.2 转速估计系统稳定性分析
与MRAS相同,状态观测器的稳定性是指状态误差的动态特性需渐进稳定,即误差能够以足够的速度收敛至零。误差动态方程为
(14)

(15)
根据Lyapunov稳定性理论来分析系统稳定性,定义
(16)

(17)
由于转速ωr在系统的每个采样周期内变化缓慢,因此在一个控制周期内近似为常数,即dωr/dt。因此对于式(17)展开整理后,设计合理的G矩阵保证其第1项为负,第2、第3项的和为零即可保证dV/dt负半定,根据此准则可得
(18)
再将式(15)代入式(18)中,可得
(19)
其中
(20)
最终整理可得估计转速的自适应律为式(21)。
(21)
3 全阶自适应观测器的仿真及结果分析
在MATLAB/Simulink平台中,搭建了全阶自适应观测器仿真,如图2所示。

图2 全阶自适应观测器仿真图Figure 2. Full-order adaptive observer
电机额定工况下的性能参数和运行数据为:额定功率3.5 kW,额定电压460 V,额定转速为1 500 r·min-1,起始给定转速为0 r·min-1,在t=0.1 s时给定转速1 500 r·min-1,在t=1.75 s减速至300 r·min-1,最后在t=3.5 s时增速至900 r·min-1。电机详细参数见表1。

表1 电机参数表
仿真结果如图3所示。

(a)

(b)图3 全阶自适应观测器转速输出图 (a)观测转速输出对比图 (b)局部转速输出图Figure 3. Rotation speed output diagram of full-order adaptive observer (a)Comparison diagram of observed speed output (b)Local speed output diagram
感应电机运行于全速范围内时,基于全阶自适应观测器的估计转速与感应电机实际转速的对比波形如图3所示。从图中可以看出,估计转速在全速范围内均可以准确跟踪实际转速,观测器在动、静态方面表现出了良好的估计性能,满足转速控制要求。
4 基于ANFIS的自适应控制器设计
4.1 自适应模糊神经网络推理系统
ANFIS将模糊系统的推理能力与神经网络的自学习能力进行了结合,通过混合学习算法找到输入和输出数据之间对应的映射关系,得到最优的隶属函数分配。ANFIS结构式类似神经网络,但功能仍是模糊系统,混合算法为倒传递和最小二乘项结合的方法。本文方案中使用具有5层ANN结构的Sugeno模糊模型[19],其结构如图4所示。
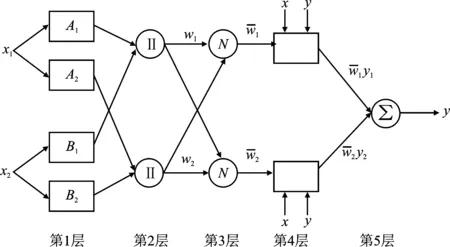
图4 模糊神经网络结构图Figure 4. Diagram of fuzzy neural network structure
第1层作为输入层,将输入变量模糊化,并且输出对应模糊集的隶属度。该层每个节点都是一个自适应节点。
(22)
若隶属函数为钟形函数,则
(23)
式中,{a,b,c}为参数设置;x1和x2为输入值;O1,i为函数隶属度;μAi和μBi分别为语言变量A和B的隶属函数;μx为一般隶属函数。
第2层的每一个节点都是固定节点,每个节点的输出表示一条规则的激励强度,该层的输出是所有输入信号的代数积。
O2,i=wi=μAi(x1)×μBi(x2)
(24)
第3层的每个节点为固定节点,将各条规则的激励强度归一化。
(25)
第4层的每个节点是有一个节点函数的自适应节点。计算出每条规则的输出为
(26)

第5层的单节点是一个带有标记Σ的固定节点。采用加权平均法将所有输入信号的总和来作为输出。
(27)
4.2 基于ANFIS的自适应PI控制器设计
为解决传统PI控制器的参数无法随系统运行而自整定的缺点,速度外环PI控制器采用ANFIS控制策略,其结构如图5所示。
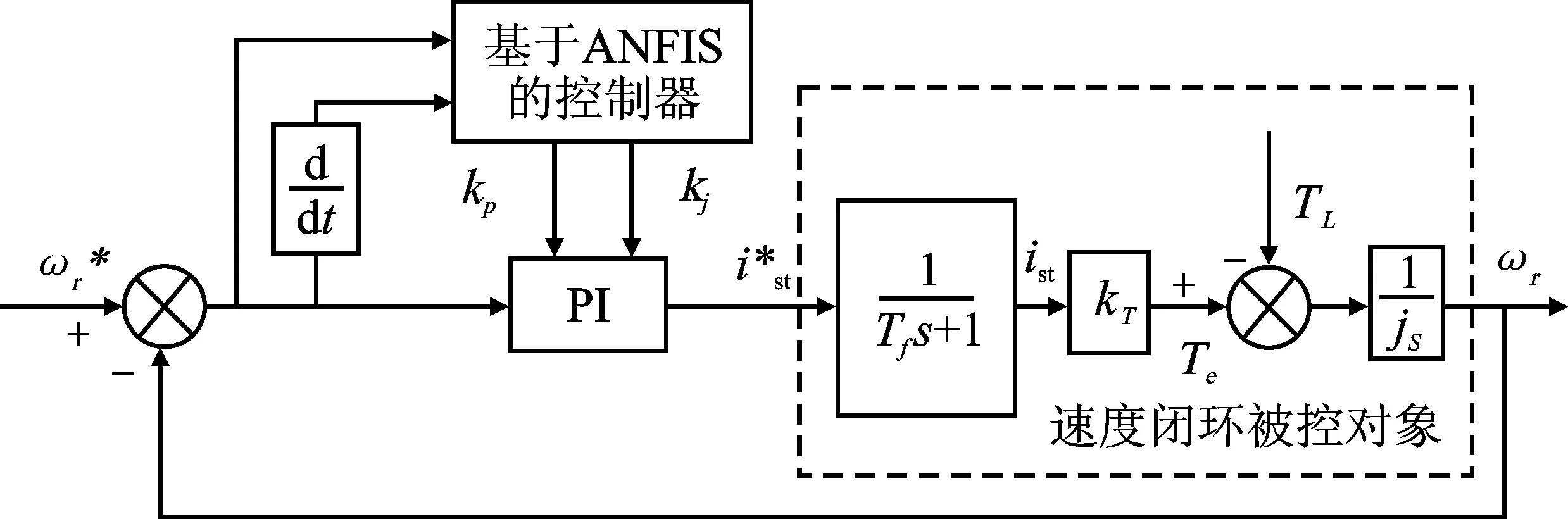
图5 基于ANFIS的控制器Figure 5. ANFIS-based controller
ANFI的输入为转速误差ec及其变化率Δec;输出为PI控制器中可变参数Kp和Ki的值。ANFIS通过混合学习算法找到输入和输出数据之间的映射关系,确定隶属函数的最优分配,根据输入变量的模糊状态而自适应调整输出,得到最佳的控制效果。本文采用在MATLAB中的ANFIS编辑工具箱来训练ANFIS。ANFIS为一阶Sugeno模型,输入量ec和Δec的模糊子集为7,模糊论域均为[-8,8],输出量Kp和Ki需根据实际情况设定,其范围分别为[0,1.3]和[0,3.3]。隶属函数为高斯函数,允许误差为10-4,训练次数为2 500,训练数据来自传统PI控制器。训练后的Kp和Ki的模糊推理输出曲面,如图6所示。

(a)

(b)图6 训练后的模糊推理输出曲面 (a)训练后的Kp模糊推理输出曲面 (b)训练后的Ki模糊推理输出曲面Figure 6. Output surface of fuzzy reasoning after training (a)Kp fuzzy inference output surface after training (b)Ki fuzzy inference output surface after training
5 仿真分析
为了验证本文提出的ANFIS控制器与全阶自适应观测器在感应电机调速系统中的可行性,在MATLAB/Simulink中进行仿真测试,电机参数如表1所示。首先进行电机的空载仿真测试,在t=0 s时给定转速500 r·min-1,然后当t=0.45 s时将给定转速提升至1 500 r·min-1,所得的仿真结果分别如图7和图8所示。然后进行转矩扰动测试,在t=0 s时给定转速1 500 r·min-1,待系统稳定后在t=0.45 s时加入了15 N·m的负载,仿真结果如图9所示。从图7和图8中可看出,在系统空载情况下相较于传统控制策略,ANFIS控制器和全阶自适应观测器所组合的新型控制策略,拥有更小的超调和更快的稳定时间。

(a)

(b)

(c)图7 传统感应电机空载仿真图 (a)转速输出波形图 (b)电磁转矩波形图 (c)三相定子电流图Figure 7. No-load simulation diagram of traditional asynchronous motor (a)Speed output waveform (b)Electromagnetic torque waveform (c)Three-phase stator current diagram

(a)
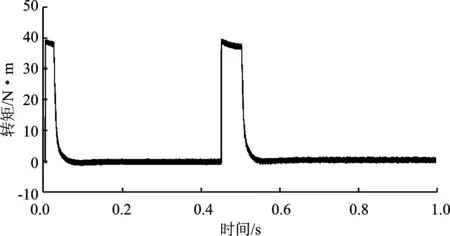
(b)

(c)

(d)图8 新型策略空载仿真图 (a)转速输出波形图 (b)电磁转矩波形图 (c)三相定子电流图 (d)ANFIS优化PI得到的最优Kp、Ki变化曲线Figure 8. New strategy no-load simulation diagram (a)Speed output waveform (b)Electromagnetic torque waveform (c)Three-phase stator current diagram (d)The optimal Kpand Ki change curve obtained by ANFIS-optimized PI

(a)
(b)

(c)

(d)图9 带载实验波形图 (a)转速输出波形图 (b)新型控制策略转速输出波形图 (c)传统控制策略电磁转矩波形图 (d)新型控制策略电磁转矩波形图Figure 9. Waveform diagram of loaded experiment (a)Speed output waveform (b)New control strategy speed output waveform (c)Traditional control strategy electromagnetic torque waveform (d) New control strategy electromagnetic torque waveform
随着系统的变化,PI控制器参数可以自适应整定,从而提高系统的动态与稳态性能。从图9可知,与传统控制方式相比,基于自适应模糊神经网络的感应电机矢量控制策略能够有效提高系统的负载转矩抗干扰能力,拥有更小的转速波动和更快的稳定时间。
考虑到Simulink中的电机模型比较理想化,与实际中的电机差距较大,因此本文在现有的电机实物参数的基础上,在Maxweel软件中搭建了相应的电机模型,使电机模型更加接近实际情况,并将此模型运用到Simulink中进行联合仿真实验。仿真结果如图10所示。

(a)

(b)
(c)

(d)

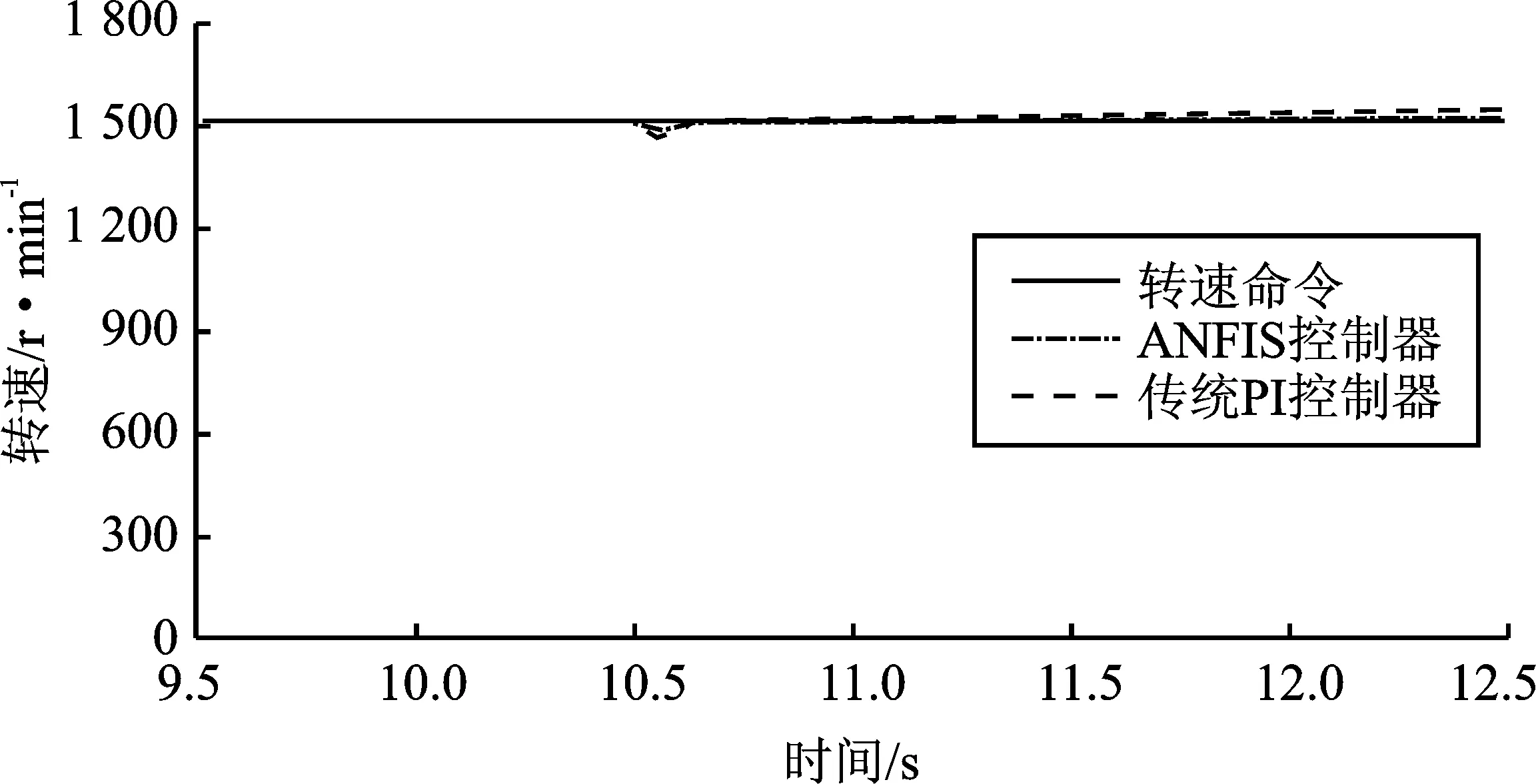
(e)图10 联合仿真实验 (a)转速响应波形图 (b)转速响应局部图 (c)突加额定负载波形图 (d)突加额定负载局部图 (e)稳态时的转速估计误差Figure 10. Co-simulation experiments (a)Speed response waveform (b)Partial graph of speed response (c)Waveform diagram of sudden increase of rated load (d)Partial drawing of sudden increase of rated load (e)Rotation speed estimation error in steady state
从图10(a)和图10(b)中可知,相比于传统PI控制器的控制策略,基于ANFIS控制器的新型控制策略具有明显的动态响应性能优势。由图10(c)和图10(d)中可知,在面对38 N·m的额定负载突加状况下,基于ANFIS控制器的新型控制策略转速跌落更小,即具有更强的抗干扰能力。从图10(e)中可知,稳态时观测器的转速估计误差大约在[-0.3,0.3] r·min-1,表明全阶自适应观测器转速辨识策略具有较高的转速辨识精度和较小的稳态误差。
6 结束语
本文通过将全阶自适应观测器和ANFIS控制器策略相结合,得出一套新的感应电机无速度传感器矢量控制方案。在感应电机的控制系统中验证了全阶自适应观测器的稳定性,通过Lyapunov理论推出自适应收敛率,观测器估计转速精度较高,满足控制要求。随着系统变化,例如当外部出现负载扰动时,相比传统方式,新型控制策略中的电机转速波动更小,并且能够更快速地恢复稳定。仿真结果表明,基于自适应模糊神经网络的感应电机无速度传感器矢量控制系统的转速估计准确稳定,可随系统的变化自适应地调节系统参数,提高了系统的自适应性和鲁棒性。

