基于改进差分进化算法的光伏最大功率点跟踪
葛传九,武 鹏,金俊喆,董祥祥,楼琦凯
(上海工程技术大学 电子电气工程学院,上海 201620)
基于现代社会生产对环保与节能的要求,太阳能已成为替代煤和石油的重要能源之一。光伏阵列在外界环境不变时,具有唯一且固定的最大功率输出工作点,即最大功率点(Maxium Power Point,MPP)。最大功率点跟踪(Maxium Power Point Track,MPPT)算法一直是光伏发电领域的热点问题。
为了在不同条件下跟踪最大功率点,研究人员提出并实施了几种MPPT技术,其中传统的跟踪方法包括扰动观察法(Perturbation and Observation,P&O)[1-2]和电导增量法(Incremental Conductance,INC)[3-4]。当光伏电池发生局部遮挡时,其功率-电压(P-U)[5-6]曲线会呈现出多极值的情况,而传统的MPPT算法无法跟踪局部阴影环境下的全局最大功率点。针对该问题,一些适用于局部阴影下的多峰值MPP算法[7-8]被提出并应用于MPP的追踪,例如粒子群优化(Particle Swarm Optimization,PSO)[9-10]算法(又称粒子群算法)、线性自抗扰(Linear Active Disturbance Rejection Control,LADRC)[11]、模糊控制(Fuzzy Logic Control,FLC)[12-13]、滑模控制(Sliding Mode Control,SMC)[14]以及混合算法控制[15]。
粒子群算法是一种常用的寻优算法,且基于群体协作的随机寻优算法具有复杂度低的优点,但粒子群算法收敛速度较慢。差分进化(Different Evolution,DE)[16]算法通过群体内个体的相互合作与竞争产生的群体智能来指导优化搜索的方向,其所采用的随机突变方式和种群更新时的竞争关系可以帮助种群提升收敛速度[17]。但是差分进化算法在MPPT过程中的占空比振幅较大,使得电路产生幅度较大的瞬时电压[18],对电路的稳定性有不良影响。
针对以上问题,本文将粒子群算法与差分进化算法结合,通过消除较差适应值粒子对种群收敛速度的影响,利用差分进化算法位置更新时的竞争进化优点,并对输出进行排序,解决了粒子群算法MPPT过程中可能出现的收敛速度慢的问题,改善了差分进化算法收敛过程中的电压振荡,实现了光伏发电系统MPPT。
1 光伏电池的多峰值曲线
在光伏发电系统中,为了提高m输出的效率,通常将多个光伏电池组串联后再并联使用[19]。在均匀的光照条件下,光伏电池模块的I-U曲线呈现单膝特性,P-U曲线呈现单峰值特性。在部分阴影下,光伏阵列的I-U曲线呈现多膝的特性,P-U曲线呈现多峰值特性。为了分析不同阴影条件下光伏组件的输出曲线,本文以3×1的串联光伏阵列为例建立模型,假设阵列中每个组件参数一致,单个电池在标准工况下(光照强度1 000 W·m-2,温度25 ℃)输出功率为60.15 W,其模型如图1所示。

图1 不同光照条件下的光伏阵列Figure 1. Photovoltaic arrays under different lighting conditions
假设环境温度为25 ℃,根据表1所示的光强度分布,得到串联光伏阵列的输出I-U曲线和P-U曲线,如图2和图3所示。
工况1中,光照强度均为1 000 W·m-2。工况2中,pv1与pv3光照强度为1 000 W·m-2,pv2光照强度为800 W·m-2,用以模拟双峰值情况。工况3中,pv1光照强度为600 W·m-2,pv2光照强度为800 W·m-2,pv3光照强度为1 000 W·m-2,用以模拟三峰值情况。

表1 光强度分布

图2 光伏阵列的I-U曲线Figure 2. I-U curve of photovoltaic array

图3 光伏阵列的P-U曲线Figure 3. P-U curve of photovoltaic array
2 PSO和DE算法
2.1 PSO算法
粒子群算法是光伏MPPT算法中常用的算法。粒子群算法中每个粒子都代表了极值优化问题中潜在的最佳解决方案。每个粒子在空间中单独搜寻最优解,将寻找到的最优值记为当前个体的极值Pbest,并将个体极值与整个种群中的其他粒子共享,比较后找到最优的个体极值作为整个种群的全局最优解Gbest。粒子群算法的基本流程为[20]:
步骤1初始化粒子种群;
步骤2计算适应值,即评价粒子;
步骤3寻找个体极值Pbest;
步骤4寻找全局最优解Gbest;
步骤5更新粒子的速度与位置。
粒子群算法中粒子的速度与位置更新计算式如式(1)及式(2)所示。
(1)
(2)
式中,vik、vik+1表示第i个粒子在k时刻、k+1时刻的速度;w表示粒子的惯性权重;c1、c2为学习因子;r1、r2为[0,1]间的随机数;Pbest,i表示第i个粒子的个体极值;xik、xik+1为第i个粒子在k时刻和k+1时刻的位置。
2.2 DE算法
DE算法的主要步骤包括变异、交叉、选择3项操作,具体步骤为[21-22]:
步骤1初始化种群。随机产生M个个体,每个个体是一个n维向量
Xi(0)=Xi,1(0)+Xi,2(0)+…+Xi,n(0),i=1,2,3,…,M
(3)
式中,Xi(0)为第0代的第i个个体;Xi,j(0)为第0代第i个个体的第j个基因;
步骤2变异。在第g次迭代中,对于个体
Xi(g)=(Xi,1(g)+Xi,2(g)+…+Xi,n(g))
(4)
生成一个中间位置向量Hi(g)。从种群中随机选择3个个体Xp1(g)、Xp2(g)、Xp3(g),且p1≠p2≠p3,则有
Hi(g)=Xp1(g)+F×(Xp2(g)-Xp3(g))
(5)
式中,Xp2(g)-Xp3(g)为差分向量;F为缩放因子,用于控制差分向量的影响力;
步骤3交叉。在第g次迭代中,对于每个个体和它所生成的中间向量进行交叉
(6)
式中,Pcr表示交叉概率;Hi,j(g)表示变异生成的后代;
步骤4选择。根据适应度函数的值。从第g次迭代的个体中间向量Vi(g)和原向量Xi(g)中选择出适应度更高的作为下一代
(7)
式中,f(Vi(g))、f(Xi(g))表示粒子适应值。
3 改进的PSO与DE算法
本文将粒子群算法的速度更新计算式进行修改后与差分进化算法融合,并增加了种群排序,提出了基于PSO和DE的改进融合算法,即IPSO-DE。
3.1 改进的更新策略
PSO算法主要靠种群个体之间的相互合作,每个粒子通过已知的个体极值和全局极值来更新自身位置。在算法中,由于粒子会向Pbest所在方向运动,随机数r1、r2和权重系数w会影响粒子向MPP移动的方向与步长。但是由于r1、r2的值是随机的,且分布于[0,1]内,因此粒子的下一个位置可能比Pbest位置差。此外,在PSO中,当部分粒子遇到较差的适应值时,这些粒子会一直存在,若Pbest恰好处于局部最大值,则会使该粒子停滞。
另一方面,DE算法采用选择和变异来强制粒子找到更佳的适应值,以便在下一代中生存。但由于DE算法内k代与k+1代的竞争关系,获胜的粒子无法保留位置记录。
为了解决以上问题,本文提出以下改进措施。为了避免部分粒子较差的个体极值使该粒子始终处于较差的位置,本文加强粒子之间的竞争关系。对速度更新计算式的修改如下
(8)
式中,Pcr表示交叉概率(本文取值为0.6)。同时,为了保持粒子前期的全局搜索能力以及后期的收敛精度,对惯性权重w、学习因子c1做如下优化
(9)
(10)

最后,结合DE算法来加速收敛。差分进化算法主要包括变异、交叉、选择3项操作。在此引用交叉和选择两项操作对粒子的速度和位置更新计算式进行修改,以此进一步提高收敛速度。先通过PSO算法更新速度,引入交叉概率,由式(8)计算决定粒子下一代的速度,而后比较适应值大小,由式(12)确定最终位置。
(11)
(12)

改进的更新策略保留了PSO算法中种群的相互合作及DE算法中粒子的相互竞争,加快了远离全局最优解的个体向全局最优解靠拢的进程,使搜索区域变得更加集中,节省了搜索时间。
3.2 种群排序
粒子种群在搜寻最大功率过程中会将更新后的占空比直接输出。由于粒子速度与位置更新具有随机性,使相邻的两个占空比间产生较大的差值。此时若依次输出占空比时,会引起电压幅值的跳变,在电路的开关器件中产生较大的尖峰电压,从而影响电路性能。
为了避免出现过大的电压幅值跳变,在输出占空比之前,对占空比进行排序。在G次迭代时按从大到小排序,在G+1次迭代时按从小到大进行排序,以此来减小由占空比的大幅跳动而引起的电压幅值跳变。
3.3 终止条件
为了加快算法收敛速度并防止在最大功率抖动的情况,本文设置了算法的终止条件,一旦跟踪到光伏最大功率点,便结束循环的执行:(1)当迭代次数iter达到预先设定的最大值itermax(本文取itermax=100);(2)如果在连续的5次迭代中满足式(13)所示条件,则循环结束。
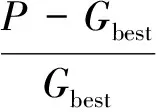
(13)
当满足以上任意一条终止条件时,结束追踪过程,直接跳出搜索循环。
综上所述,得到基于改进粒子群算法与差分进化算法的混合MPPT控制总流程,如图4所示。

图4 基于IPSO-DE混合算法总流程Figure 4. General flow of hybrid algorithm based on IPSO-DE
4 仿真结果及分析
在理论分析的基础上,对基于IPSO-DE和PSO、DE算法的光伏系统使用MATLAB/Simulink进行单峰值及多峰值工况下的仿真验证。
4.1 单峰值情况下的仿真验证
首先仿真验证单峰值工况。按图1所示的工况1结构进行搭建,最大功率为60 W。遵循表1中工况1相关参数设置光照,并采用3块串联的光伏电池来模拟系统。PSO、DE和IPSO-DE对光照部分遮蔽环境下的最大功率追踪曲线分别如图5、图6和图7所示。

图5 单峰值环境下PSO算法的功率追踪过程Figure 5. Power tracking process based on PSO algorithm in single peak environment

图6 单峰值环境下DE算法的功率追踪过程Figure 6. Power tracking process based on DE algorithm in single peak environment

图7 单峰值环境下IPSO-DE算法的功率追踪过程Figure 7. Power tracking process based on IPSO-DE algorithm in single peak environment
4.2 多峰值情况下的仿真验证
按图1所示的工况3结构进行搭建,最大功率为122 W。遵照表1中工况3相关参数对光照进行设置,并采用3块串联的光伏电池来模拟系统。PSO、DE和IPSO-DE对光照部分遮蔽环境下的最大功率追踪曲线如图8、图9和图10所示。

图8 部分遮蔽环境下PSO算法的功率追踪过程Figure 8. Power tracking process based on PSO algorithm in partially shielded environment

图9 部分遮蔽环境下DE算法的功率追踪过程Figure 9. Power tracking process based on DE algorithm in partially shielded environment

图10 部分遮蔽环境下IPSO-DE算法功率追踪过程Figure 10. Power tracking process based on IPSO-DE algorithm in partially shielded environment
在部分遮蔽环境下,功率追踪过程的电压波动分别如图11、图12和图13所示。

图11部分遮蔽环境下PSO算法的电压追踪过程Figure 11. Voltage tracking based on PSO in partially shaded environment

图12 部分遮蔽环境下DE算法的电压追踪过程Figure 12. Voltage tracking based on DE in partially shaded environment

图13 部分遮蔽环境下基于IPSO-DE算法的电压追踪过程Figure 13. Voltage tracking based on IPSO-DE in partially shaded environment
4.3 仿真结果分析
在对多峰值工况进行的仿真模拟中,PSO耗时0.90 s,追踪到功率为122.06 W;DE耗时1.12 s,追踪到功率为122.04 W;IPSO-DE耗时0.43 s,追踪到功率为122.08 W。在追踪到相同MPP的前提下,IPSO-DE所耗时间比PSO所耗时间减少了52.22%,比DE所耗时间减少了61.60%。
在最大功率追踪的过程中,PSO、DE和IPSO_DE在电压波动的抑制如表2所示。

表2 PSO、DE和IPSO-DE收敛过程中的电压波动
由表格中的数据对比可知,在追踪过程的中期,IPSO-DE对电压波动幅度有明显的抑制作用,对电压波动的抑制效果优于PSO与DE。
5 结束语
本文利用DE算法具有选择和竞争的优点,将其与粒子群算法相结合,重新设计了粒子的速度更新机制,并对输出的粒子位置即占空比进行排序来减小电压波动。通过仿真验证,比较了IPSO-DE和PSO、DE在最大功率追踪上的效果。结果表明,在光照遮蔽的多峰值条件下,IPSO-DE可以在保证收敛精度的前提下,缩短收敛时间,有效抑制中后期的电压波动。

