基于自适应VSG控制的光伏并网系统
孙思男,郝正航
(贵州大学 电气工程学院,贵州 贵阳 550025)
随着化石能源的减少,新能源发电技术逐渐受到人们的重视。针对光伏逆变器控制策略的研究中,以恒功率控制、电压频率控制以及下垂控制的研究最为广泛。恒功率控制依靠锁相环技术从电网获取频率和相位,通过功率外环和电流内环的设计使系统可以输出给定的有功功率和无功功率[1]。电压频率控制策略是通过电压电流双闭环来实现的。当输出功率发生小范围波动时,该控制可以维持电压和频率的稳定[2]。下垂控制则是通过模拟发电机的外特性对有功功率和无功功率进行分别控制[3]。光伏电源需要通过逆变器接入大电网,但逆变器本身不具有惯性和阻尼,抗扰动能力较差,需要通过相应逆变器控制维持系统稳定。然而,上述控制策略无法为光伏逆变器提供所需的惯性和阻尼,在一定程度上削弱了系统的稳定性。
从2008年开始,陆续有研究人员将传统同步发电机(Synchronous Generator,SG)的转动惯量和阻尼系数引入光伏逆变器,提出虚拟同步发电机(Virtual Synchronous Generator,VSG)控制策略[4]。该策略通过模拟同步电机转子特性,使得光伏逆变器拥有惯性和阻尼,提高了并网系统的稳定性[5-7]。文献[8]针对负载扰动的系统提出一种新的VSG控制,通过调节转动惯量起到抑制频率和功率波动的作用。
文献[9]提出了基于储能的变换器在恒功率模式和VSG下垂模式下进行互换的双模式控制策略。该策略虽能实现平滑切换,但参数设定仍有改进的空间。文献[10]分析了孤岛运行下的VSG控制策略。在负载改变时,记录频率变化率,适当地选取转动惯量的值,并通过模拟各种工况验证了此方法的优越性。但该研究并没有详细说明转动惯量取值方法,且对于判据整定运算和系统暂态特性分析方面的研究略有不足。文献[11]为了增大风电系统本身的调频能力,通过调整转动惯量选取提出改进的自适应控制,最终实现了系统安全运转。文献[12]所提控制策略在一定程度上提高了系统的功率和频率抗扰动能力,但该研究没有提及调整系数的选择方法。文献[13~14]所给出的自适应旋转惯量虚拟同步机控制策略仅仅适用于运行孤岛模式,且对并网模式并未研究。文献[15]在风电系统中采取VSG策略,提升风电系统频率的稳定性,但是对于虚拟同步型风机的虚拟转动惯量和阻尼等参数的选取尚未形成统一的整定规则。文献[16]研究了风电系统的虚拟惯量控制。该研究分别分析了比例系数和微分系数下的系统频率、并网功率和转速的变化情况,但功率振荡问题仍需进一步改进。文献[17]提出了风电系统的虚拟惯量控制,模拟了不同工况下各个量的变化情况,并仿真验证了该控制策略对降低电网频率振荡的有效性。文献[18]在系统的逆变环节加入VSG控制,使其具备自主参与调频等同步发电机外特性。虽然系统的稳定性有所增强,但负荷变化时的系统调频特性仍不理想。文献[19]提出光储系统的VSG控制策略,但转动惯量和阻尼没有随系统变化,系统动态调节能力欠佳。
目前,关于虚拟同步发电机转动惯量的研究较多,但在转动惯量和阻尼系数相结合领域的研究较少。本文提出一种改进的VSG控制,从功角关系和频率波动角度进行分析,通过增减转动惯量和阻尼系数达到调整频率和有功功率的目的,使其尽快结束暂态过程。本文将改进的控制策略应用于光伏并网系统中,并在MATLAB/Simulink上进行了仿真分析。仿真结果表明,相较于传统的VSG控制,改进VSG控制下的光伏并网系统动态响应性能更好。
1 光伏并网的传统VSG控制策略
在光伏微网中,光伏逆变器本身不具备惯性和阻尼,以往的逆变控制策略均不能提供相应的惯性调节。此外,电力电子器件响应速度较快,当负载发生变化时,系统频率出现波动,对大电网产生冲击。因此,通过系统中加入惯性环节来减少对电网的依赖是必要的。现有的电力网大多采用同步发电机进行惯性调节,同步电机转子旋转时产生转动惯量,转子部分产生的大量动能导致同步发电机拥有较大惯性。转子上的阻尼绕组在通过电流时所产生的磁场下的转矩可以减小电机的振荡,因此可增设系统阻尼。基于同步发电机的结构特点以及可以提供惯性的特性,出于对光伏并网系统稳定性的考虑,本文提出了虚拟同步机控制策略,其整体结构如图1所示。
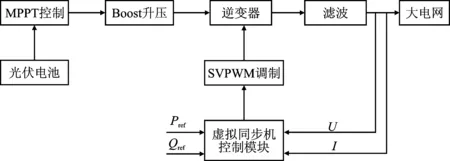
图1 光伏并网VSG控制结构图Figure 1. Diagram of photovoltaic grid-connected VSG control structure
1.1 虚拟同步发电机
本文所采用的是虚拟同步发电机的两阶模型,其整体结构示意图如图2所示。其转子运动方程为
dδ/dt=ω
(1)
(2)
式中,δ表示的是功角(单位为rad);ω表示的是电气角速度(单位为rad·s-1);Tm表示的是机械转矩(单位为N·m);Te表示的是电磁转矩(单位为N·m);Pref表示的是给定功率(单位为W);Pe表示的是实际输出有功功率(单位为W);J表示的是转动惯量(单位为kg·m2);D表示的是阻尼系数(单位为N·m·s·rad-1);ω0表示的是电网同步角速度(单位为rad·s-1),极对数取为1;Td=D(ω-ω0)为阻尼转矩(单位为N·m)。该结构中的逆变器输出电压eabc乘以并网侧的电流iabc获得Pe,电磁转矩计算式为
Te=Pe/ω=(eaia+ebib+ecic)
(3)
根据基尔霍夫电压定律, VSG的并网电流表达式为
L(di/dt)=eabc-uabc-Riabc
(4)
式中,L本为逆变器的滤波电感,充当SG与之相对应的电抗;R本为输电线上的电阻,充当SG与之相对应的电枢电阻;uabc是VSG网侧机端电压;eabc是VSG控制的逆变器输出电压。
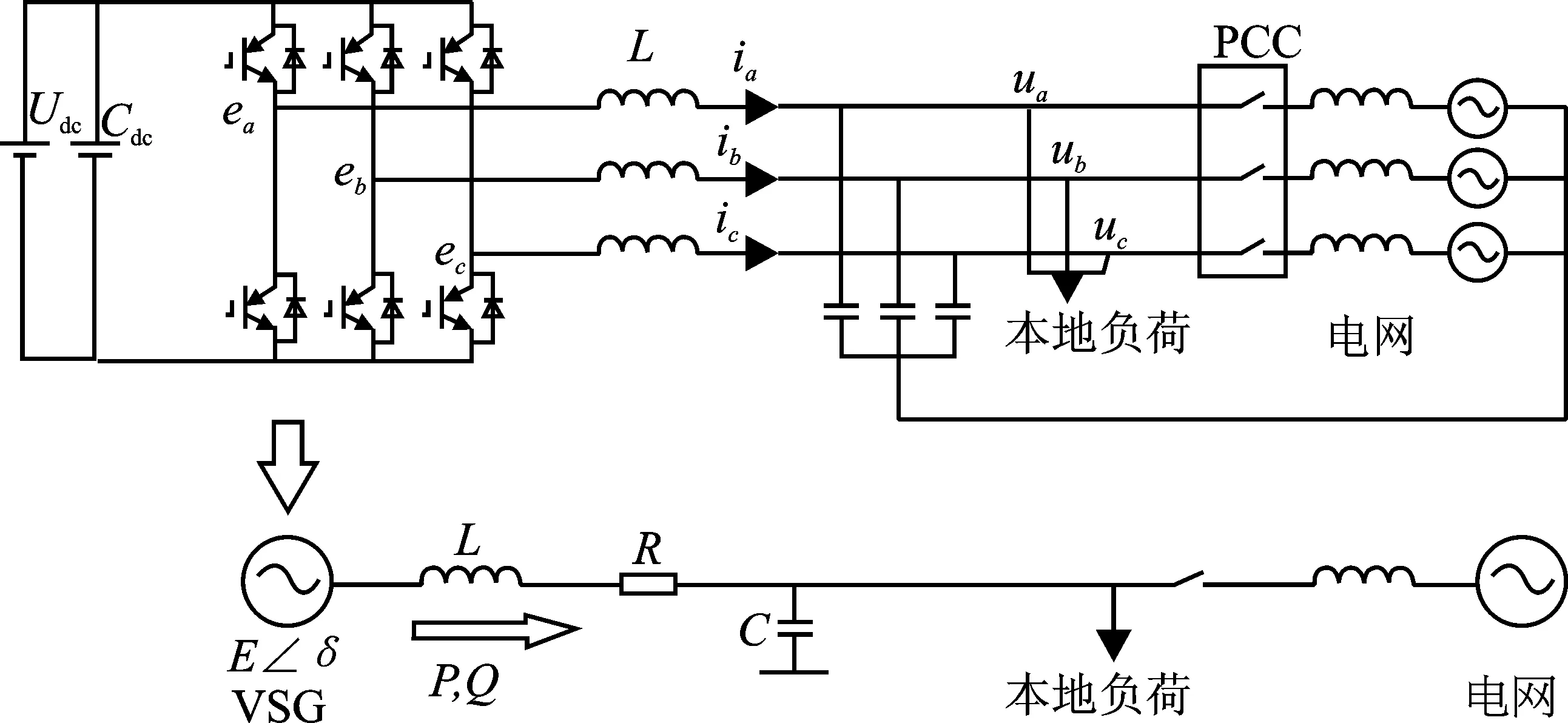
图2 虚拟同步发电机结构Figure 2.Virtual synchronous generator structure
1.2 并网逆变器的VSG控制策略
本文采用类似同步电机中自动调频装置实现对频率偏差的调节。将阻尼转矩Td=D(ω-ω0)充当调频器,合理选取阻尼转矩来调节电网频率偏差。通过控制虚拟同步电机机械转矩实现对有功功率的调整,具体表达式如式(5)所示。
Tm=Pref/ω
(5)
无功的调节为:由给定的无功功率与真实测的无功功率进行相减,并进行积分处理,然后将积分后的数值再乘以相应的无功功率调整参数。具体形式如下
(6)
式中,E1表示调整无功电势;kq表示调整无功参数;Qref表示给定无功功率;Q表示真实测的无功功率。
电压的调节为:给定的电压与真实测的电压相减,所得的差值再乘以电压的调整参数。电压调整的计算式为
(7)
式中,E2表示调整电压电势;kv表示调整电压参数;Uref表示给定电压;U表示真实测的电压。VSG的电势E是VSG空载电势E0、调整无功电势E1以及调整电压电势E2的和,即
E=E0+E1+E2
(8)
因此,VSG的电势可以进一步写成
(9)
式中,Ep为相电压的幅值,数值上等于E乘以根号下2/3。
综上所述,得到如图3所示的控制策略,并选择比例谐振控制器跟踪电流iabc。在无静差的前提下,一般采用给定电流irefabc来求解有功功率和无功功率。
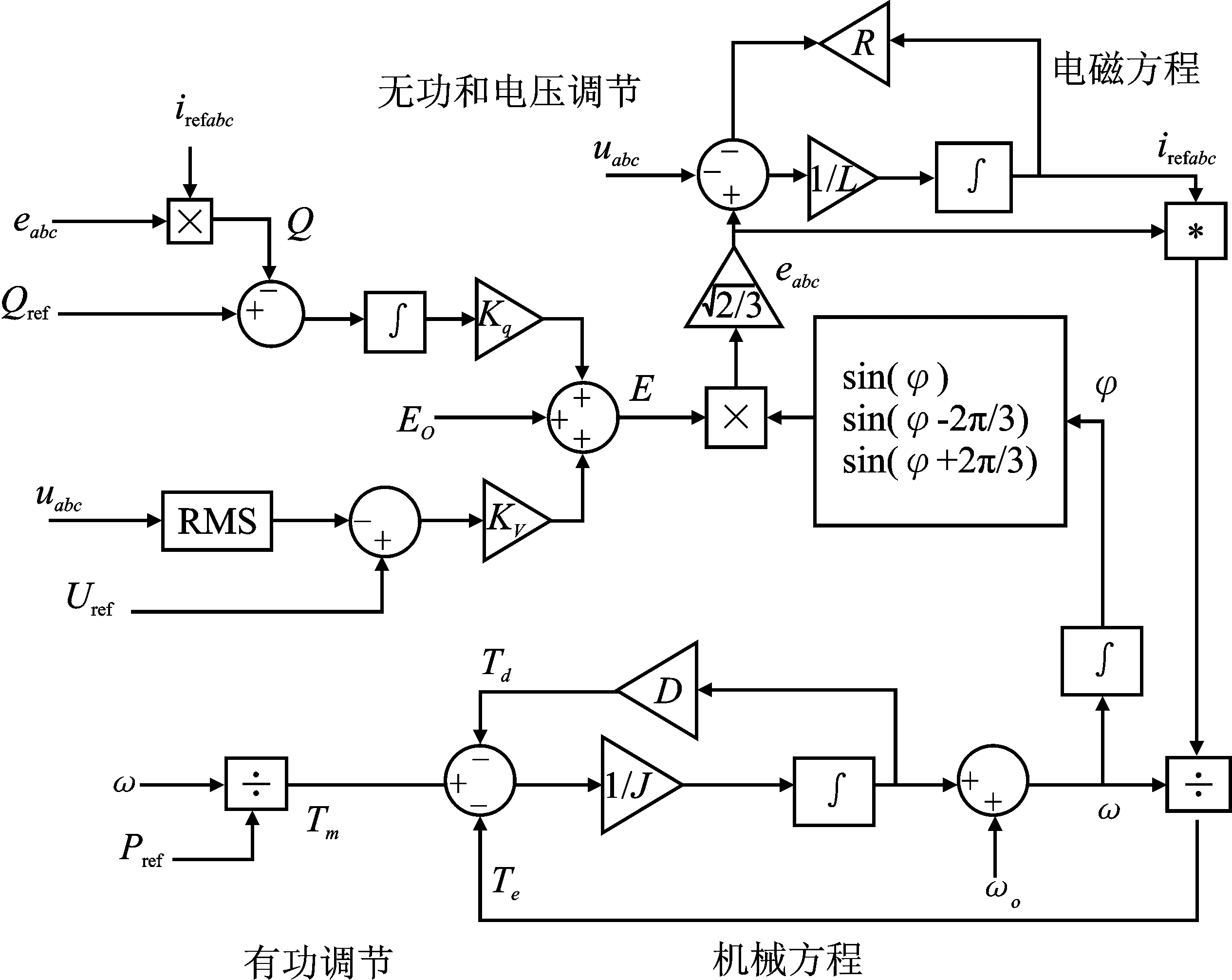
图3 并网逆变器的VSG控制策略Figure 3. VSG control strategy of grid-connected inverter
2 光伏并网的改进VSG控制策略
2.1 改进控制
同步电机的功角关系曲线及在暂态过程中的频率波动情况如图4所示。图4(a)的①~④分别对应于图4(b)的t1~t2、t2~t3、t3~t4、t4~t5共4个时间段,这4个时间段组成一个完整的暂态过程。VSG波动过程与该暂态过程相类似,两者均可看作衰减振荡。
对一个完整暂态振荡过程的分析为:
(1)第1阶段中,转子角频率从电网的同步角速度ω0开始增加, dω/dt大于0,ω始终大于ω0,即第1阶段为加速阶段。当到达功率P2时,△ω的绝对值达到最大值。为了防止其越限对系统造成不良的影响,这时应增大系统的惯性来减小角速度的偏移量,减缓角速度的变化速度,所以应适当增大J和D;
(2)第2阶段是速度不断下降的一个时期。尽管ω0依然要小于ω,但此时转子的角频率的变化率是小于0的,转子的角频率开始逐渐靠近电网同步角速度。然而,此时的功角依然在不断增大。为了防止功角越限,并且为加快系统响应速度,保证第2阶段尽快结束,应降低系统惯性的大小,即降低J并适当提高D的大小;
(3)第3阶段的变化和调节过程与第1阶段类似;
(4)第4阶段的变化和调节过程与第2阶段类似。
一个振荡周期完整的暂态过程由上述4个阶段组成。在第3及第4阶段中,同样需要对J和D进行调整,此处不再赘述。需要注意的是,上述分析的4个阶段均在假设J和D保持不变的条件下进行。

(a)
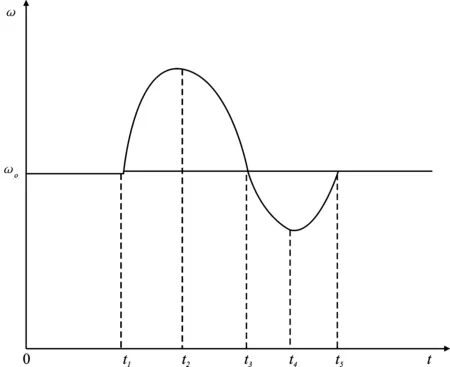
(b)图4 同步发电机功角和频率振荡曲线 (a)功角 (b)转子角频率振荡Figure 4. Synchronous generator power angle and frequency oscillation curve (a)Angle (b)Rotor angular frequency oscillation
综上所述,J的选择由Δω和dω/dt共同决定,D的选择则由Δω决定。不同情况下J和D的选择规则如表1所示。

表1 不同情况下转动惯量和阻尼系数的选取原则
结合J和dω/dt的相互关联性、D和Δω的相互关联性以及表1中不同情况下转动惯量和阻尼系数的选取原则,改进控制策略如下所述:
(1)对于转动惯量J,当Δω(dω/dt)≤0或|dω/dt|≤Tj时,J=J0;当Δω|dω/dt|>0∩|dω/dt|>Tj时,J=J0+Kj|dω/dt|;
(2)对于阻尼系数D,当|Δω|≤Td时,D=D0;当|Δω|>Td时,D=D0+Kd|Δω|。其中,J0为平稳运转时VSG的转动惯量,D0是VSG平稳转动时的阻尼系数,Kj为转动惯量的调整参数,Kd为阻尼系数的调整参数,Tj和Td为给定的限定值。转动惯量与阻尼系数的自适应控制流程如图5和图6所示。

图5 转动惯量自适应控制原理Figure 5.Principle of adaptive control of moment of inertia

图6 阻尼系数自适应控制原理Figure 6. Principle of adaptive control of damping coefficient
2.2 参数整定
一套完整的系统参数整定方案是保证系统运行良好的关键。SG的转动惯量主要由同步电机本身大小以及它的额定功率决定。通常,H表明SG的惯性强弱,本文的H指惯性时间常数,计算式为
H=Jω0/Sn
(10)
式中,时间常数H表示在额定的转矩下SG空载所花运动时间,这个运动时间是指从速度为0到达到额定转速消耗的时间;Sn是SG额定容量。SG通用的模型推导过程为
(11)
dδ/dt=ω-ω0
(12)
ωr=(ω-ω0)/ω0
(13)
由式(11)~式(13)可得
dδ/dt=ω0ωr
(14)
式中,ωr为转速偏差标幺值,在式(2)等式两边同时乘同步角速度与同步发电机的额定容量比值可得
J(dω/dt)ω0/Sn=(Tm-Te)ω0/Sn-D(ω-ω0)ω0/Sn
(15)
等式左边为
J(dω/dt)ω0/Sn=H(dωr/dt)
(16)
TB=Sn/ω0
(17)
(18)
式(17)表示转矩的基准值。将式(17)、式(18)代入之后可得等式右边为
(19)
式中,上标“*”表示为标幺值,功率和转矩之间的标幺值关系满足
P*=T*ω*
(20)
当ω*为1时,功率和转矩的标幺值相等,所以式(19)还可以如式(21)所示。
(21)
因此VSG的通用模型可以描述为
dδ/dt=ω0ωr
(22)
(23)
在已知同步发电机的额定容量和电网同步角速度的情况下,根据惯性时间常数的计算式可求得系统的转动惯量。结合式(22)、式(23),并借鉴传统同步发电机的小信号模型分析方法,可得到虚拟同步发电机的小信号稳定分析模型,具体结构如图7所示。
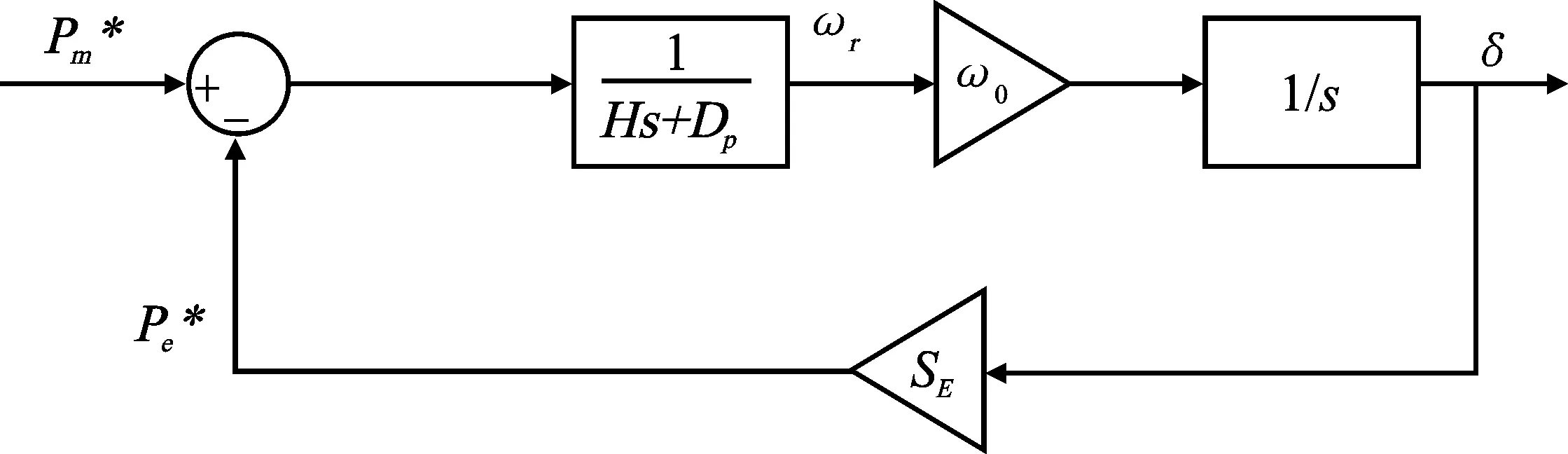
图7 同步发电机小信号稳定模型Figure 7. Small-signal stability model of synchronous generator
如图7所示,该系统为反馈系统。由此,可以写出其传递函数如式(24)所示。
(24)
对式(24)化简,可得VSG的输入功率响应特性和输出功率响应特性为
(25)
将式(25)写成以下形式
(26)
对比式(25)和式(26)可得出ωn和ξ的具体形式。
(27)
(28)
通过最优参数整定方法,令系统的阻尼比ξ=0.707,可得到较快响应速度和较低超调量。阻尼参数表达式为
(29)
式中,SE表示同步功率的标幺值,可根据以下计算式进行计算
(30)
式中,U为电网电压;δ这里取δs;Es和δs均为与指令功率有关的稳态运行点。Es、δs、α、Z的计算式为
(31)
(32)
α=tan-1(ωL/R)
(33)
(34)
式中,L和R是同步电感和同步电阻;Pref为给定有功功率;Qref为给定无功功率。
(35)
根据式(35)可得阻尼系数D的值。由控制原理可知,随着转动惯量J的增大,系统频率稳定性变差;随着阻尼系数D的增大,系统频率稳定性逐渐增强。调节系数kj和kd以及Tj和Td需按照系统的具体情况进行选取,以保障系统频率尽快趋于稳定。
3 仿真分析
3.1 负载不变时各量在两种控制下的仿真对比
为了说明在负载不发生变化的情况下,光伏并网系统采用改进VSG控制策略后的性能,本文在MATLAB/Simulink上进行了仿真,并对本文所提策略及传统VSG控制策略下的角频率、有功功率、无功功率以及并网电流的波动情况进行了分析和比较,结果如图8~图11所示。
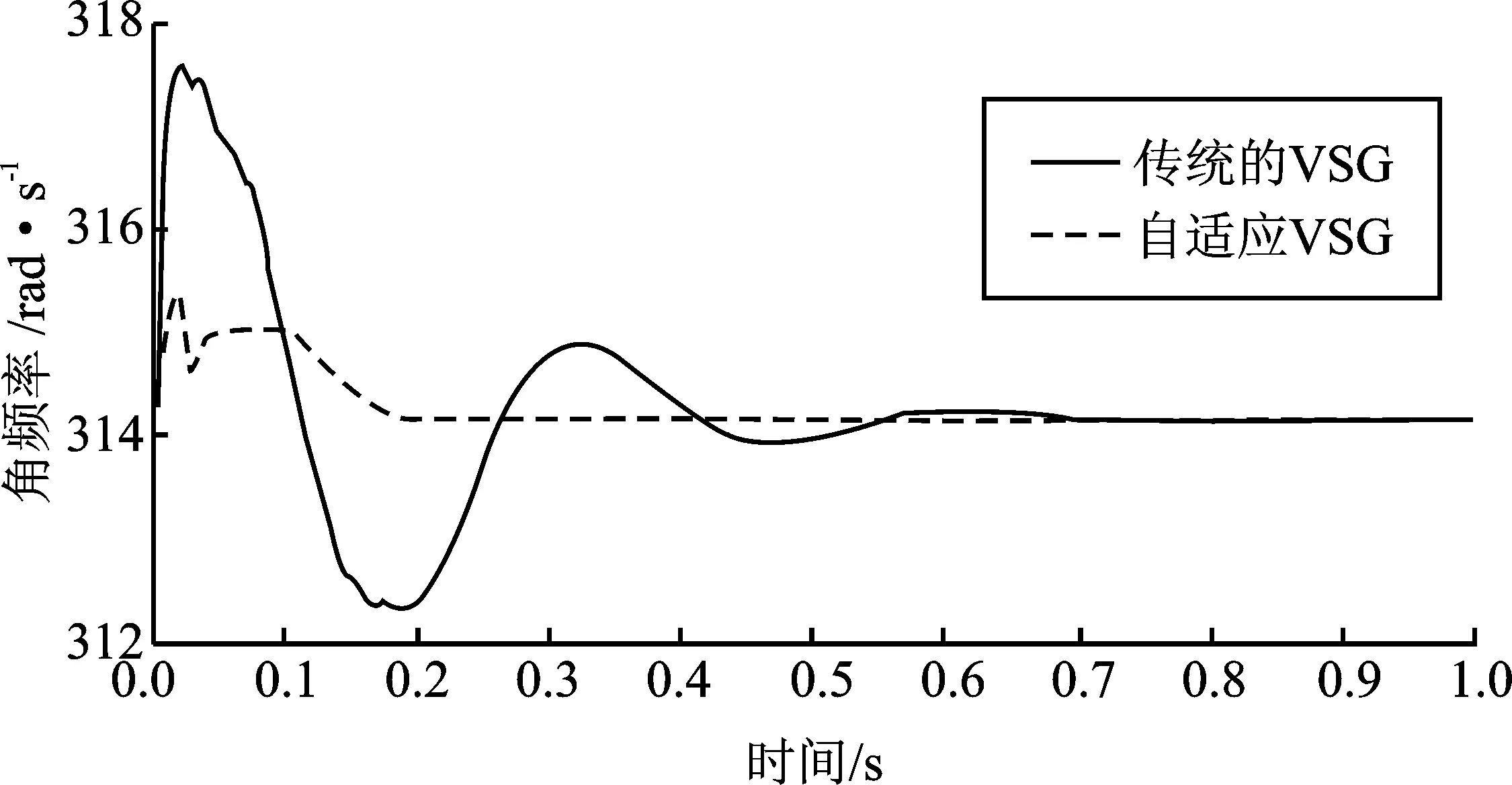
图8 VSG控制改进前后的角频率对比Figure 8.Angular frequency comparison before and after the improvement of VSG control
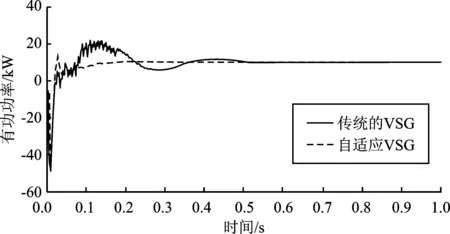
图9 VSG控制改进前后的有功功率对比Figure 9.Comparison of active power before and after the improvement of VSG control

图10 VSG控制改进前后的无功功率对比Figure 10.Comparison of reactive power before and after the improvement of VSG control

图11 VSG控制改进前后下的并网电流对比Figure 11.Comparison of grid-connected current before and after the improvement of VSG control
从在传统VSG和改进VSG下的角频率、有功功率、无功功率以及并网电流的仿真结果可以看出,在减缓波动和降低超调方面,采用改进VSG后的波动程度和超调量都更小,说明本文所提改进控制策略性能更好。
3.2 负载改变时各量在两种控制下的仿真对比
在仿真模型中,原先为5 000 W的有功负载在0.7 s时阶跃变化到8 000 W。
图12~图15分别表示当有功负载在0.7 s发生变化之后的角频率、有功功率、无功功率以及并网电流在传统VSG和改进VSG下的仿真波形对比。可以看出,改进VSG控制下的角频率、有功功率、无功功率相比传统VSG控制可更快地趋于稳定,波形也相对更加平缓。对于并网电流来说,虽然负载有所变化,但电流数值几乎没有变化,改进后的VSG控制下的谐波抑制更加明显。由于在0.7 s之前的角频率、有功功率、无功功率以及并网电流与负载没有发生变化的时候类似,此处便不再赘述。
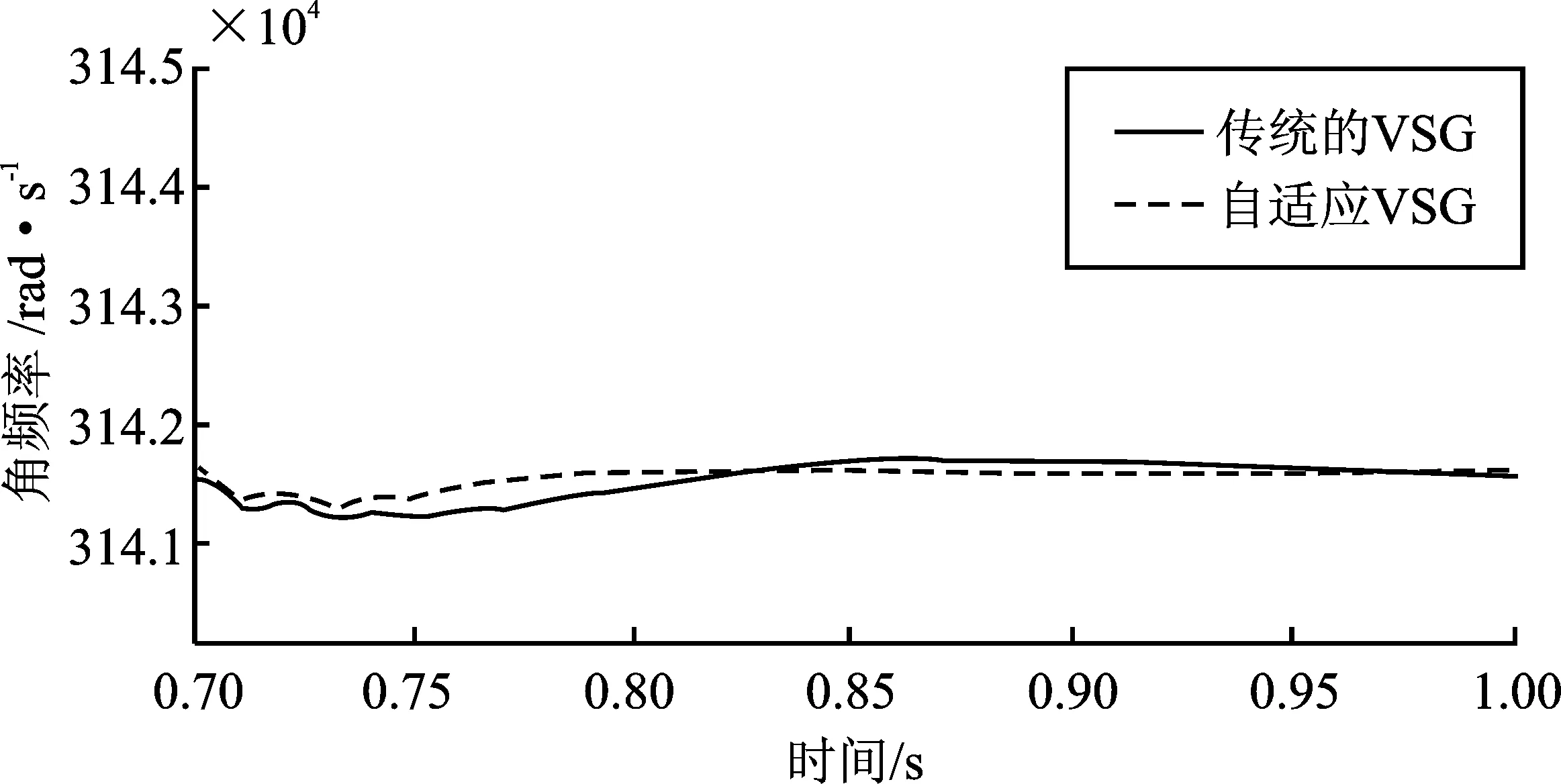
图12 传统VSG和改进后VSG下的角频率对比Figure 12. Comparison of angular frequency between traditional VSG and improved VSG

图13 传统VSG和改进后VSG下的有功功率对比Figure 13. Comparison of active power between traditional VSG and improved VSG
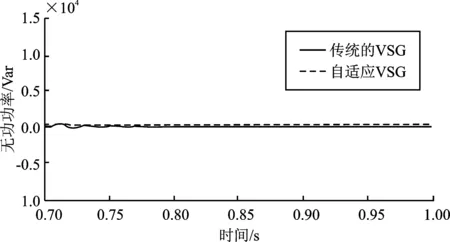
图14 传统VSG和改进后VSG下的无功功率对比Figure 14. Comparison of reactive power between traditional VSG and improved VSG

图15 传统VSG和改进后VSG下的并网电流对比Figure 15. Comparison of grid-connected current between traditional VSG and improved VSG
4 结束语
本文以光伏并网系统为背景,针对传统VSG控制下系统动态响应欠佳的情况,从功角与有功功率之间的关系及暂态过程中的角频率变化情况切入,得出不同情况下转动惯量和阻尼系数的选取原则。本文结合转动惯量和角频率变化率之间的关系,以及阻尼系数与角频率变化量之间的关系,设计了改进的VSG控制策略。通过MATLAB/Simulink模拟了在负载不变和负载发生变化两种工况下的角速度、有功功率、无功功率以及并网电流仿真波形图。仿真结果表明,基于改进VSG自适应控制策略下的光伏并网系统较传统VSG控制动态响应性能更好,更有利于系统安全稳定运行。

