典型破片侵彻靶板的动能表征方法

杨 喆，马重阳，周英麒，商 飞，张恒庆

(南京理工大学，南京 210094)

1 引言

杀爆类战斗部爆炸破片是目标杀伤的核心毁伤元，破片动能是破片毁伤威力最直接、最重要的表征参量，爆炸场破片动能的准确测量对于杀爆类战斗部毁伤威力评估及实战应用具有重要的军事意义。

令人遗憾的是，在爆炸场极端毁伤工况下破片动能的准确测量难度较大，至今尚未研究出有效的测试手段。当前杀爆类战斗部破片动能测试方法主要是将破片动能视为导出量，分别测量出破片速度和破片质量，通过公式=12×间接测量破片动能。破片速度通常采用铝箔靶、梳状靶、光幕靶等区截装置测量得到，该方法测量的速度本身精度有限，其次测量所得速度为破片区间平均速度，无法准确回推至某点瞬时速度值；战斗部预制破片数量庞大，无法准确测量记录每一枚破片质量，只能采用平均质量作为统一记录，质量量值精度存在偏差。综上所述，现有破片动能测试方法存在较大的局限性，制约了杀爆类战斗部的发展进程。

爆炸驱动破片撞击靶板表面，侵彻目标形成破片孔，导致目标撕裂或出现较大形变，该部分能量损耗表现为破片动能降低，损耗的破片动能最终以固定特征的弹性波形式释放为应变能，即为声发射；基于此原理，使得从能量转换角度获得破片动能成为一个可能的思路。

声发射检测技术(Acoustic Emission)作为一种被动无损的实时监测方法，具有主动性、几何形状不敏感性、实时性、特征性等优点，现已被广泛应用于石油化工、电力、楼房、桥梁、隧道大坝、航空航天、交通运输行业的容器检测、复合材料性能试验、结构状态监测等领域。广西大学的罗丹旎等研究了界面I-II复合型断裂力学行为及声发射特征，其研究结果表明利用声发射特征参量的突变能够有效判断起裂和失稳临界状态，从而揭示界面断裂损伤演化规律。李杰等通过煤岩膨胀破裂实验,分析了煤岩膨胀破裂全过程应变与声发射信号的变化规律，为煤岩致裂等工程的监测预警提供依据。樊国伟、尚军宁等通过对不同含水量条件下的煤体破裂过程进行研究，分析得到该条件下的声发射特征与撞伤演化规律。胡永辉、张国强等研究了不同参数(包括粒子大小、撞击速度、材料类型和撞击位置)对检测到的AE信号的影响。声发射检测技术在工程检测方面的应用比较广泛，且利用声发射技术进行状态分析的可行性得到充分的验证。Prosser曾对薄板撞击声发射信号进行了试验研究和分析,给出了撞击损伤程度与信号频率之间的关系；国内唐颀、庞宝君等则利用声发射技术分别对撞击源定位和波动在结构中的传播模式进行了研究,基于声发射的撞击损伤技术在轨预测撞击损伤程度。截至目前，国内外未见利用声发射技术开展破片动能测试的探索研究。

本研究利用ANSYS有限元分析平台，模拟不同动能破片侵彻靶板的过程，获取靶板内声发射信号，提取典型的声发射信号特征参量，考察其与动能参量的相关性，为进一步研究破片撞击靶板的声发射能量特征关系奠定基础。

2 典型破片侵彻靶板模拟分析

2.1 模型建立

采用ANSYS有限元分析软件建立侵彻破片与目标靶板二维模型，并对破片撞击靶板过程中的声发射信号进行仿真模拟，由于球形破片撞击铝合金靶板的二维模型具有轴对称性，其对称轴为球形破片的中心轴线，故建立1/2模型即可满足要求。采用TUNG.ALLOY钨合金球形弹丸作为模拟破片，破片半径为4 mm；采用AL7039铝材料为靶板材料，靶板厚度为1 mm，破片距离靶板0.01 mm；撞击界面尺寸设定为400 mm×400 mm，即在二维对称模型中，靶板厚度1 mm，靶板高度200 mm；

选取ANSYS软件中自带的材料模型参量，材料参数如表1所示；钨合金和AL7039状态方程采用Shock，强度模型采用Johnson Cook，侵蚀模型采用Geometric Strain；破片速度仿真范围800～2 000 m/s，步长50 m/s，以轴正方向作为破片速度的正方向；设置参数固定靶板边界条件，破片和靶板采用拉格朗日算法，网格划分均为0.1 mm。为了声发射信号的完整性并减小应变能对声发射信号的干扰，在距离中轴线30 mm处设置高斯积分点，若高斯点设置的过远，会延长仿真运行时间，若高斯点设置的过近，破片撞击靶板产生的形变会干扰声发射信号的准确测量。仿真模型如图1所示。

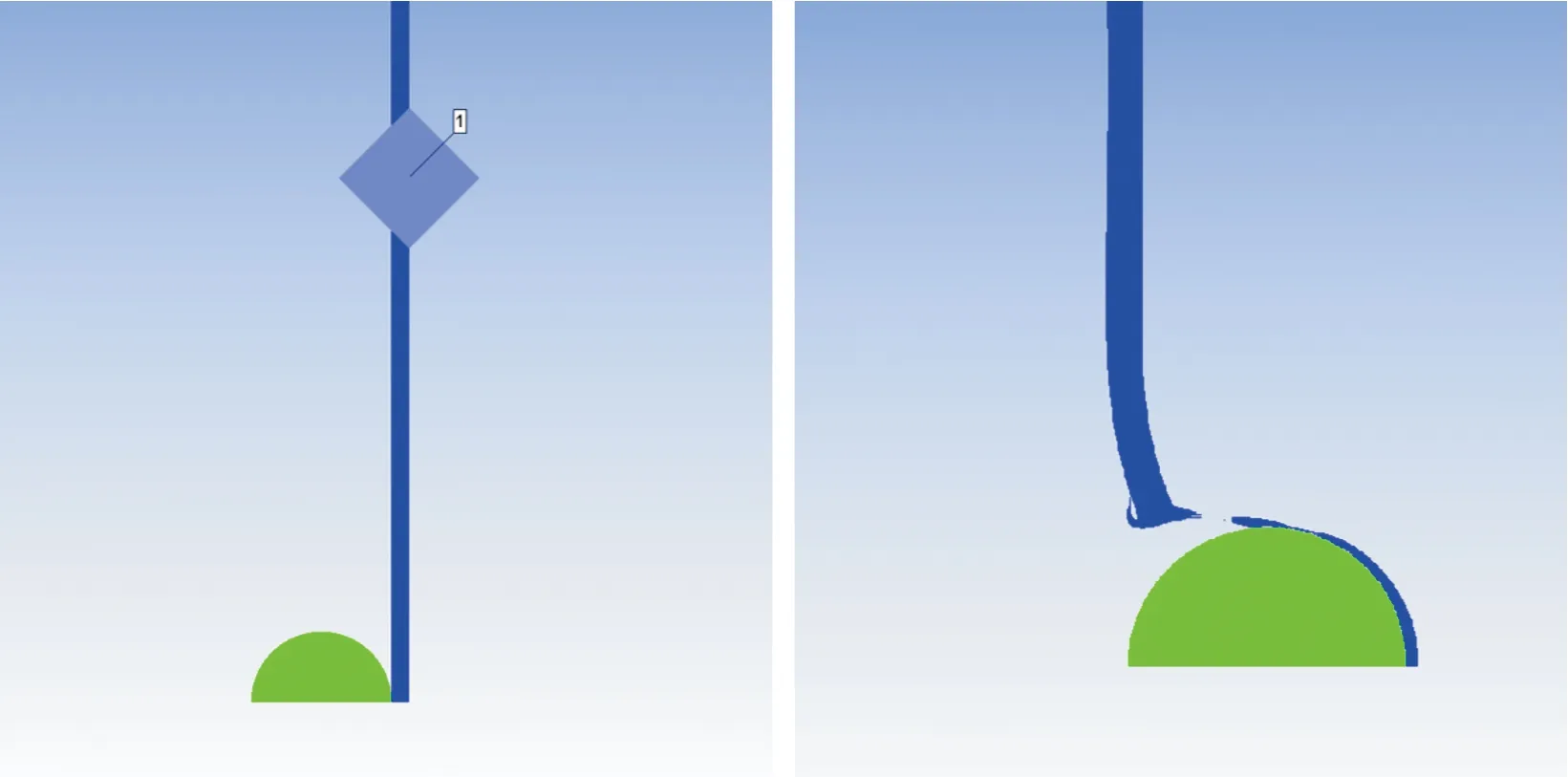
图1 仿真模型示意图Fig1 Schematic diagram of simulation model

表1 7039铝和钨合金材料参数Table 1 AL7039 and TUNG.ALLOY material parameters

2.2 仿真数据处理

根据声发射理论及经验数据，仿真获取破片碰撞靶板时高斯点法向速度随时间变化曲线视为声发射信号。

声发射信号通常包括上升时间、峰值计数、振铃计数、能量、持续时间、幅度、均方根值(RMS)以及信号强度等多个表征参量。破片侵彻靶板初始动能最终转化为靶板内弹性波能量及破片剩余动能，需要根据数据判断破片动能与声发射信号诸多表征参量中关联度最大的一项作为动能测量数据源，为进一步构建声发射信号-破片动能转换模型奠定基础。

破片与靶板的作用过程包含破片撞击、侵彻靶板、靶板变形、产生断裂4个过程。声发射信号存在衰减传播和反射的过程，在声发射信号传播到采样点一段时间后，靶板边缘的反射信号到达采样点，该信号与源信号极其相似，信号识别上存在困难，为了避免边缘反射信号干扰，提出基于声发射信号曲线特征的经验算法分辨入射信号。声发射入射信号与反射信号在时间上存在延迟，基于此特征可以将声发射信号与边缘反射信号区分开来，并最大限度地确保声发射信号的完整性，取靶板边缘反射信号的开始的时间作为提取有效声发射信号的终止时间。具体操作在于取一固定值作为数据有效值的起点，声发射信号的终点求取所进行的数据处理依次为微分、滑动平均、数据平滑、取绝对值，经过上述步骤，所获得的声发射曲线将在反射信号开始的时间存在明显的上升沿，取固定值作为基准用来区分声发射信号与反射信号。

保持破片质量不变，步进调整破片速度以改变破片动能。以1 mm厚度的AL7039靶板在受到速度为900 m/s，半径4 mm的TUNG.ALLOY球形破片撞击时的声发射信号为例，其完整声发射信号如图2所示。

图2 破片速度900 m/s的完整声发射信号曲线Fig.2 Complete acoustic emission signal of fragment velocity 900 m/s

经过滑动平均算法与进一步差分，将仿真声发射信号的分解为的趋势信号与残余信号，并采用前文提到的声发射信号有效值部分提取经验算法，获得有效声发射趋势信号和有效声发射残余信号分别如图3所示。

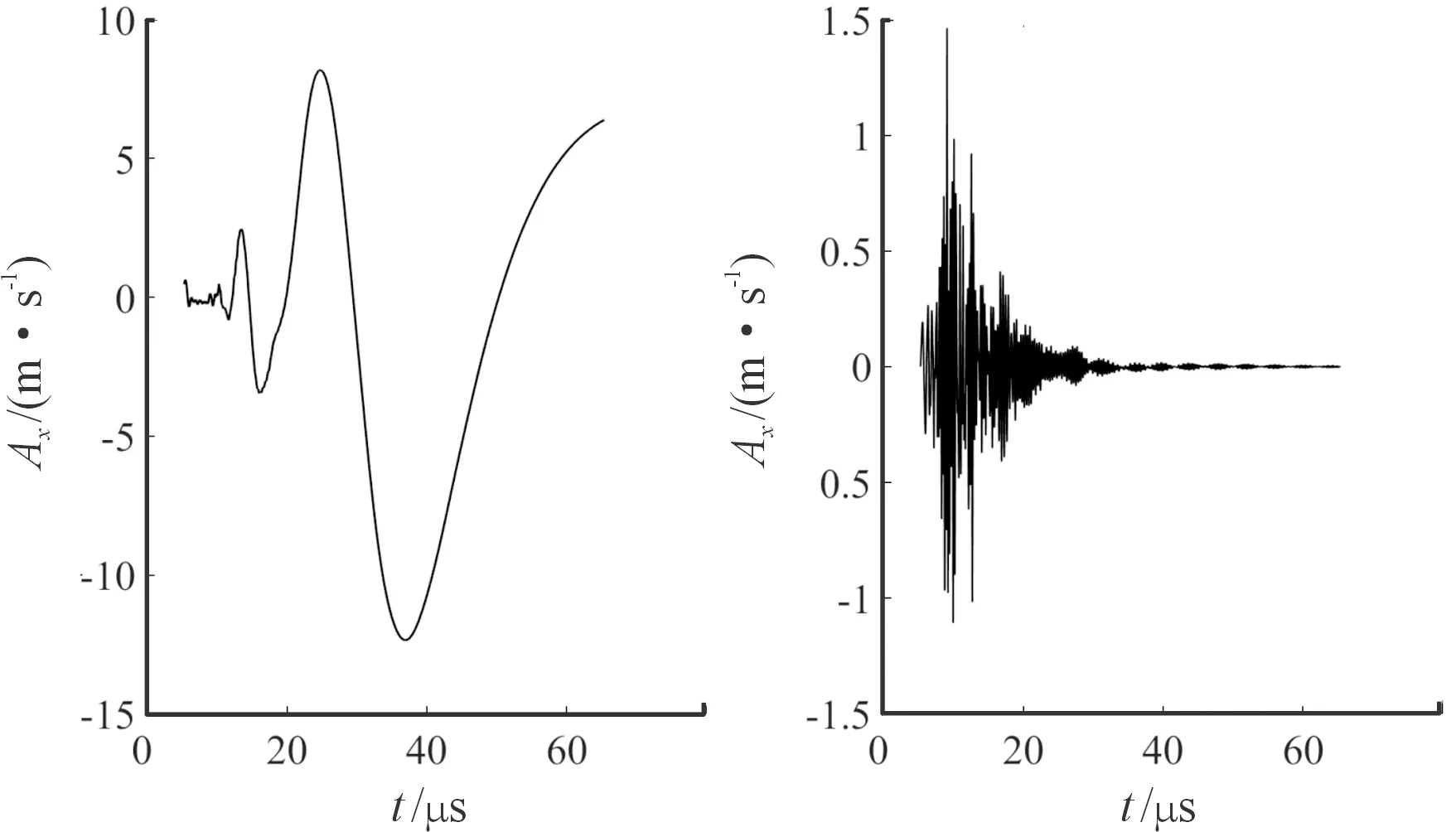
图3 经上述算法获得的破片速度900 m/s的有效声发射趋势信号与残余信号曲线Fig.3 The effective AE trend signal and residual signal of fragment velocity 900 m/s obtained by the above algorithm

3 声发射表征参量研究

3.1 表征参量提取

针对经过滑动平均算法与本文中提出的声发射信号提取的经验算法获取到的声发射有效趋势信号，分别提取了均方根值、信号的平均值、峰值、峰谷、方差、峰度、偏度、持续时间等特征参量。图 4～图9可见，有效趋势声发射信号平均值、峰度、偏度、持续时间等有效趋势声发射信号表征参量在一定区间内波动，与引发声发射信号的破片动能无明显的关联性；有效趋势信号的峰值、峰谷、RMS值、方差均与破片动能成一定的函数关系。

图4 不同破片动能下信号的均值和持续时间变化曲线Fig.4 Variation diagrams of mean and duration of signals under different fragment kinetic energy

图5 不同破片动能下信号的峰度和偏度变化曲线Fig.5 Variation diagrams of kurtosis and skewness of signals under different fragment kinetic energy

图6 不同破片动能下声发射信号的峰谷及拟合曲线Fig.6 Minimum value and fitting curve of acoustic emission signal under different fragment kinetic energy

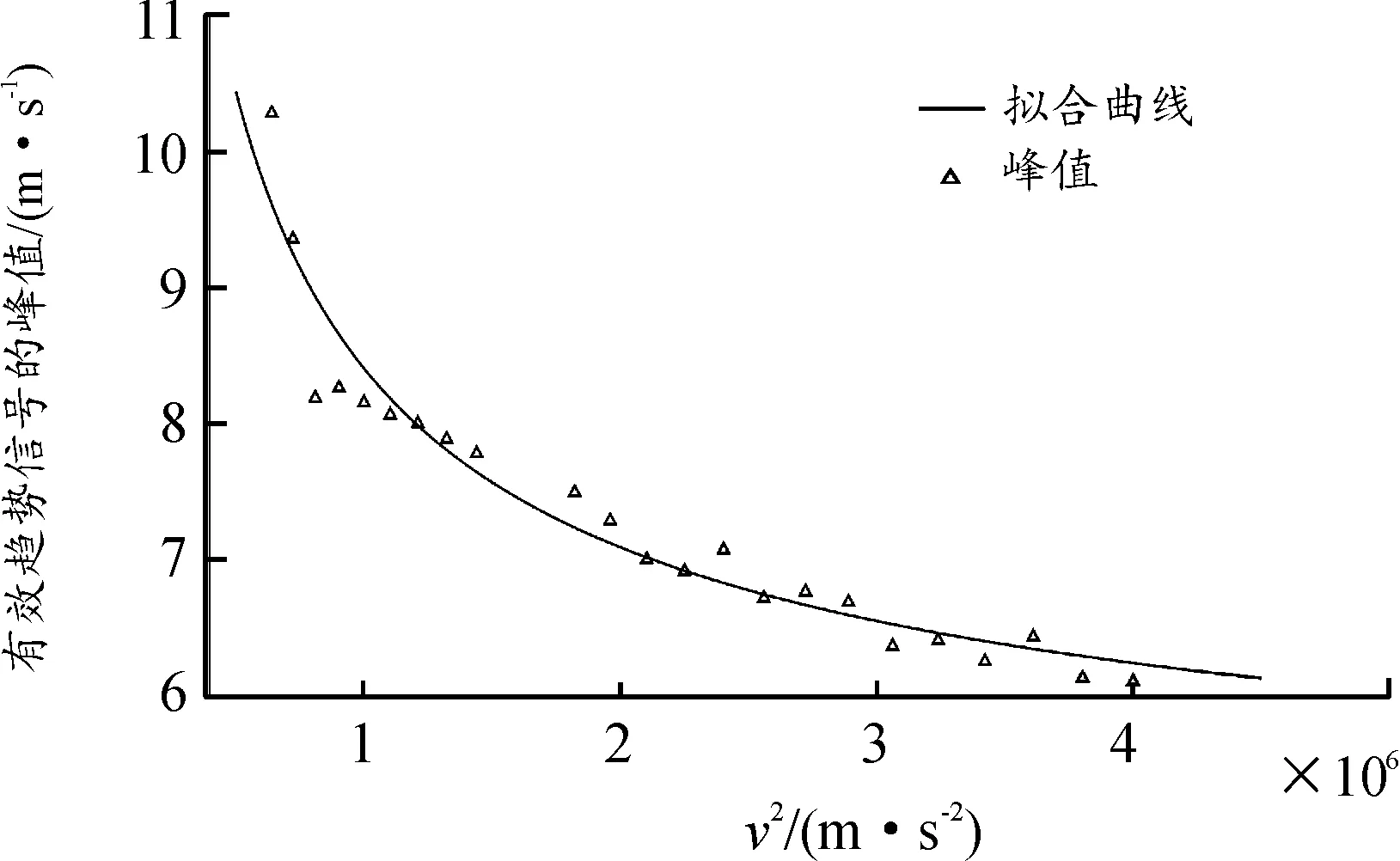
图7 不同破片动能下声发射信号峰值及拟合曲线Fig.7 Peak value and fitting curve of acoustic emission signal under different fragment kinetic energy

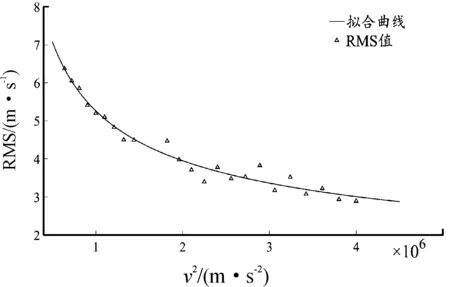
图8 不同破片动能声发射信号RMS值及拟合曲线Fig.8 RMS value and fitting curve of acoustic emission signal under different fragment kinetic energy

图9 不同破片动能下声发射信号的方差及拟合曲线Fig.9 Variance and fitting curve of acoustic emission signals under different fragment kinetic energy

典型的残余声发射信号的时域特征有一定的波动性，所有特征参量均在某一范围内波动，在破片动能较低时或者破片的动能区间较小时可以应用，但不适合大动能区间的破片动能表征。

随着破片动能增加，材料应变率提高。当破片速度处于1 250～1 300 m/s时，由塑性变形产生的热量增多，应变硬化导致的流变应力的上升不足以抵抗热软化导致的流变应力的下降，此时热软化作用占主导地位,由Johnson-Cook本构模型可知，材料屈服极限发生改变；同时破片动能的增加导致破片撞击压力提高，产生的破碎粒子向速度相反的方向溅射，影响侵彻的稳定性，表现在声发射各参数数据中：① 当速度在1 250～1 300 m/s附近时，各参数均发生了较大的数据离散，与曲线整体趋势不符；② 如图 10、图11所示为破片速度在1 200～1 350 m/s时0～20 μs的声发射曲线图。

图10 破片速度1 200 m/s、1 350 m/s的20 μs 内声发射信号曲线Fig.10 0～20 μs acoustic emission signals at fragment velocities of 1 200 m/s and 1 350 m/s

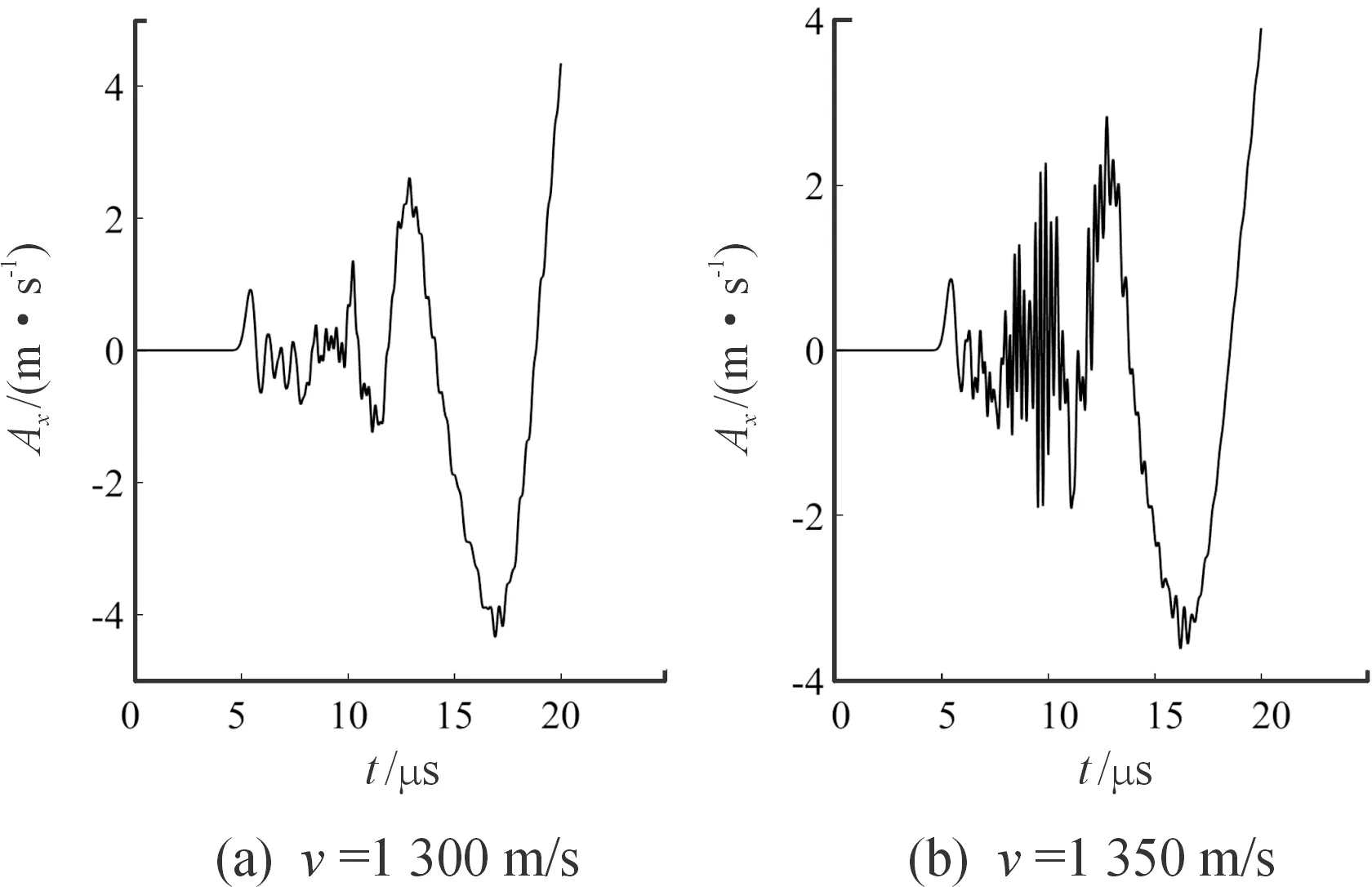
图11 破片速度1 300 m/s、1 350 m/s的20 μs 内声发射信号曲线Fig.11 0～20 μs acoustic emission signals with fragment velocities of 1 200 m/s and 1 350 m/s

由图10、图11可以看出，当破片速度在1 250～1 300 m/s附近时，声发射信号在0～20 μs内，其波动性较低，与其他速度区间内的声发射信号不同。故将破片速度在1 250～1 300 m/s附近时的声发射信号特征参量引入模型会引入较大的模型误差，故在计算模型时将该值舍去。

3.2 动能模型建立

针对上述与破片动能显示出一定函数规律的峰值、峰谷、RMS值、方差，分别进行函数拟合。

声发射趋势信号的四项特征参量随破片动能增加大致呈现幂函数变化规律，破片动能与声发射特征参量函数模型设定为：

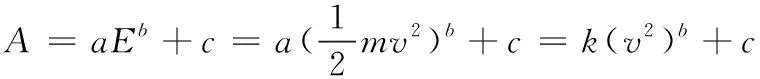
式中：为声发射信号的特征参量，在本文模型中分别对应峰谷、峰值、值、方差；为破片动能；为破片速度；、、、为模型系数。

30 mm处声发射趋势信号的峰值、峰谷、RMS值、方差与典型破片动能的散点与拟合曲线如图6—图9所示。拟合模型的特征参量如表2所示。

表2 部分拟合模型的特征参量Table 2 Fitting comparison of some parameter models

通过上述模型的对比，声发射趋势信号的峰谷与破片动能的幂函数拟合系数最大且均方根误差相对较小，可用来表征破片动能。

不同破片动能下声发射趋势信号的峰谷值如图6所示，随着破片动能的增加，峰谷值不断增大。

声发射信号的峰值与破片动能的拟合系数为0.991 6，均方根误差(RMSE)值为0.238 4，该模型表明在误差允许的范围内，有效趋势声发射信号的峰谷值与破片动能具有显著的幂函数关系。

4 结论

破片与铝合金靶板发生超高速碰撞时，两者实现质量、动量和动能的重新分配；通过对破片撞击靶板产生的信号特征参量分析得到结论：① 声发射趋势信号的平均值、持续时间、峰度、偏度等特征参量与破片动能无显著对应规律，不适合表征破片能量；② 声发射趋势信号的峰值、RMS值、方差与破片动能呈现一定的对应规律，在保持其他变量一定的情况下，随着破片动能不断提高，声发射信号的该项特征值越小；③ 破片撞击靶板产生的声发射趋势信号的峰谷与破片动能具有显著的幂函数对应关系。