论函数的可导与分数阶可导

刘书霞，詹华税

(厦门理工学院数学与统计学院，福建 厦门 361024)

导数是微积分学中最基本最重要的概念[1-4]。长期以来，导数一直受到众多学者的不间断的研究和讨论。文献[5]利用闭区间连续函数的最值原理论证了二元函数的梯度的重要性；文献[6]利用定义讨论分段函数在分界点处的可导性；文献[7-8]讨论了某类分段函数的一些求导方法；文献[9]通过一些例子展示了如何用不同的方法求分段函数的分段点处的导数；文献[10]研究了分段函数求导理论在退化抛物方程解唯一性讨论中的一些具体应用。总体而言，除文献[11] 之外，尚未发现有其他学者研究仅在一点可导的函数性质。同时，尚未发现有关导数四则运算、反函数求导法、复合函数求导法这些常用求导方法彼此间相互依存关系的研究。

近年来，分数阶导数理论及其应用越来越受到数学物理界、工程力学界、生物医学界学者的广泛关注，其在建筑学、核物质、黏弹性材料、数学建模甚至是天气预报、地震波的预测等领域都有广泛的应用[12-16]。另外，即便是经典的整数阶导数，也还有一些理论需要补充和完善[17-18]。而对于分数阶导数的理论和应用研究，除了Riemann-Liouville分数阶导数和Caputo分数阶导数之外，还有其他不同的分数阶导数的定义[19]。

为此，本文针对经典整数阶导数研究的空白点，从是否存在一点可导的相关函数和求导法则间相互关系的视角讨论函数的可导性问题；在分析一元分段函数在分界点处的导数问题和总结分段函数求导法的基础之上，引进Riemann-Liouville分数阶导数定义和Caputo分数阶导数的定义，探讨分数阶导数与整数阶导数的相容性问题，研究次数为μ>0分数阶可导问题。

1 函数的可导性

1.1 仅在一点可导的相关函数的构造

注意到函数y=f(x)关于连续和可导都是逐点定义的，那么是否存在仅在一点连续的函数？是否存在仅在一点可导的函数？下面例子给出这样的函数的构造。

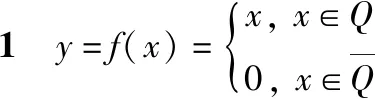
定理1初等函数在其定义域区间内连续。

关于导数，初等函数未必在其定义域内都可导。但比定理1弱的结论有定理2。

定理2初等函数在其定义区间内几乎处处可导，即除去一个零测度集外，其他点都可导。

证明只要对基本初等函数的四则运算和有限次复合运算后所得到的函数在其定义区间内几乎处处可导就可以了。

重要的是，定理2中的初等函数的条件不能减弱为连续函数，因为Weierstrass、Waerden等已给出了处处连续但处处不可导的例子。f(x)在x点不可导，可能是f(x)在该点表现为尖点，所以要构造一个处处连续但不可导的例子的一个方法便是不断增加尖点的密度。

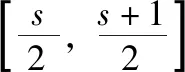
结合例2、例3，存在处处连续但只在一点可导的例子，只要修正例3的构造即可。

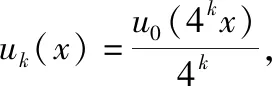
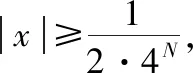
例4可以回答以下问题1和问题2。

问题1是否存在一个只有一点存在二阶导数的连续函数?

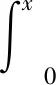
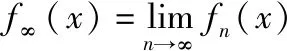
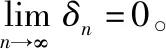
1.2 求导法则间的关系

熟知，求导数的方法有四则运算法则、复合函数求导法则、反函数求导法则、对数求导法、参数方程求导法等。下面论述它们之间的依存关系。

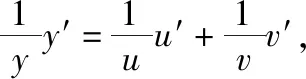
就求导方法而言，复合函数求导法更重要。理由如下：

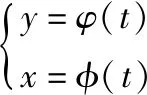
2 分数阶可导问题

2.1 一元分段函数在分界点处的导数问题

一元分段函数在分界点处的导数问题可简单归纳为以下2点：1)根据可导必连续，不连续一定不可导，可先判断是否连续，若不连续，则函数在该点不可导；2)在分界点处连续的情况下，一般都是利用定义判断是否可导。在分界点处连续的情况下，还可以采用另一种方法判断可导性。

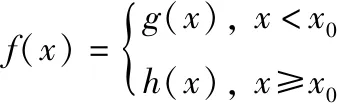
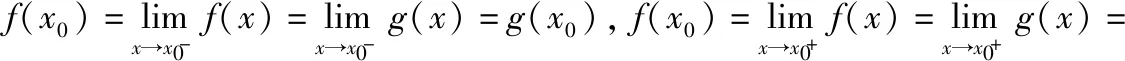
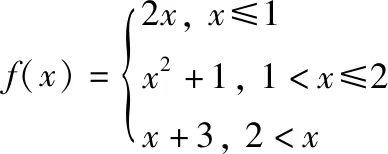
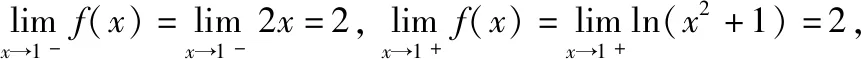
2)在x=2处，显然在该点连续，x2+1及x+3在包含x=2的某邻域可导，但是(x2+1)′|x=2=4≠(x+3)′|x=2=1，由定理3可知f′(2)不存在。

可以看出，此种方法比定义法简洁。当然，分段函数还有其他诸多可以研究的性质，比如，如何将一元函数的分段函数推广到多元函数。特别需要着重指出的是，分数阶导数正是以分段函数的形式来定义的。

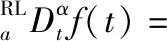
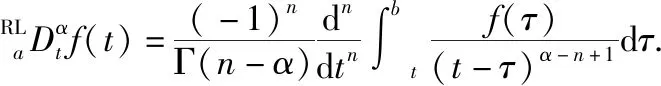
当0<α<1,n=[α]+1=1时，如果f(t)在[a,t]上二阶可导，有：

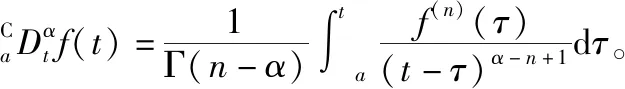
当0<α<1,n=[α]+1=1时，如果f(t)在[a,t]上二阶可导，有

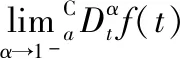
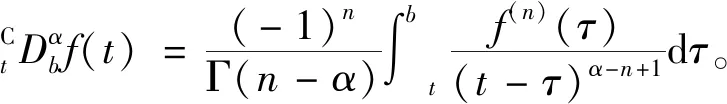
基于以上分析可知，这2种分数阶导数都是普通导数的合理推广。并且发现，对于分数阶导数，因为是左、右分数阶导数分别定义的，所以考虑分段函数的分数阶导数是没有意义的。当然也可以考虑以左、右分数阶导数存在且相等来定义分数阶导数在某一点的可导性，但目前没有见到这方面的讨论。另外，虽然Riemann-Liouville分数阶导数和Caputo分数阶导数都是普通导数的推广，但从定义1和定义2可以看出，Caputo分数阶导数首先要求f(t)是可导的，甚至要求在二阶可导的条件下才能推断出它与普通导数的相容性。

2.2 分数阶导数与整数阶导数的相容性

下面讨论Riemann-Liouville分数阶导数、Caputo分数阶导数与经典整数阶导数的相容性问题。这个问题可以直接从Riemann-Liouville分数阶导数和Caputo分数阶导数的定义来导出。

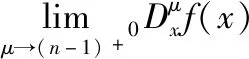
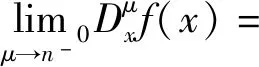
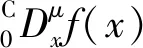
3 结论

本文从导数定义出发，通过研究导数的相关性质及其在分数阶导数的推广，得到了以下结论：

1)构造出仅在一点可导的函数及其他相关函数。

2)导数的加法运算在四则运算中最为重要，复合函数的求导法在求导方法中最重要。

3)Riemann-Liouville分数阶导数和Caputo分数阶导数都是普通导数的推广；Riemann-Liouville分数阶导数与经典整数阶导数具有相容性，Caputo分数阶导数与经典整数阶导数的相容性略差。

本文的结果有助于进一步开展分数阶微分方程等解的存在性、唯一性和大时间渐近等的研究工作。