lnverse scattering transforms of the inhomogeneous fifth-order nonlinear Schrödinger equation with zero/nonzero boundary conditions

Jin-Jin Mao，Shou-Fu Tian，Tian-Zhou Xu and Lin-Fei Shi

1 School of Mathematics and Statistics，Beijing Institute of Technology，Beijing 100081，China

2 School of Mathematics，China University of Mining and Technology，Xuzhou 221116，China

Abstract The present work studies the inverse scattering transforms (IST) of the inhomogeneous fifth-order nonlinear Schrödinger(NLS)equation with zero boundary conditions(ZBCs)and nonzero boundary conditions(NZBCs).Firstly，the bound-state solitons of the inhomogeneous fifth-order NLS equation with ZBCs are derived by the residue theorem and the Laurent’s series for the first time.Then，by combining with the robust IST，the Riemann-Hilbert(RH)problem of the inhomogeneous fifth-order NLS equation with NZBCs is revealed.Furthermore，based on the resulting RH problem，some new rogue wave solutions of the inhomogeneous fifth-order NLS equation are found by the Darboux transformation.Finally，some corresponding graphs are given by selecting appropriate parameters to further analyze the unreported dynamic characteristics of the corresponding solutions.

Keywords: the inhomogeneous fifth-order nonlinear Schrödinger equation，inverse scattering transforms，Darboux transformation，bound-state soliton，rogue wave，zero/nonzero boundary conditions

1.lntroduction

As one of the current research focuses，the nonlinear evolution equations (NLEEs) with zero/nonzero boundary conditions have been brought to the forefront of nonlinear systems in the past decades [1–4].Many effective methods have emerged to get the solutions for NLEEs.In 1967，Gardner et al first proposed the inverse scattering transforms(IST)and applied it to the Korteweg–de Vries(KdV)equation[5].The classical IST methods are generally studied on the basis of the Gel’fand-Levitan-Marchenkoo integral equation.In 1987，Zakharov et al appropriately predigested the IST method by issuing the Riemann–Hilbert (RH) formula [6].Subsequently，more and more researchers used this method to obtain the soliton solutions of many NLEEs[7–13].Thereby，the research on the RH formula made important progress in the field of integrable systems，which is remain popular all around the world [14–30].

In recent years，the study of bound-state (BS) solitons and rogue wave(RW)solutions based on the RH method have drawn much attention，thereby more and more BS solitons and RW solutions of the NLEEs have been found.In 1972，Zakharov and Shabat derived the multiple-poles(MPs)soliton solutions of the nonlinear Schrödinger (NLS) equation [31].Thereafter the increasing MPs solitons of different nonlinear integrable equations have been solved，for example，the modified KdV equation [32]，the sine-Gordon (sG) equation [33]，the Sasa-Satsuma(SS)equation[34]，the Wadati-Konno-Ichikawa(WKI)equation[35]，and the complex modified KdV equation[36].In addition，they discussed the asymptotic for MPs solitons[37，38].Most importantly，using the original IST method to solve the BS solitons，which requires not only a lot of calculations but also some complex constraints [32，33].However，the RH problem with MPs can be directly expressed by employing the residue theorem and Laurent’s series[35，36]，which not only simplifies the calculation but also obtains the BS solitons.Thereafter，Bilman and Miller found that the robust IST can be applied to solve the higher-order RW solutions of the focusing NLS equation [39].Simultaneously，this method is used to solve breather wave solutions，rational W-type soliton solutions，and so on.Afterward，the robust IST is used to solve more nonlinear integrable equations of RW，such as the fifth-order NLS equation[40]，the sixth-order NLS equation [41]，the Hirota equation [42]，the quartic NLS equation [43]，and the generalized NLS equation [44].

In this paper，we mainly study the inhomogeneous fifthorder NLS equation [45]

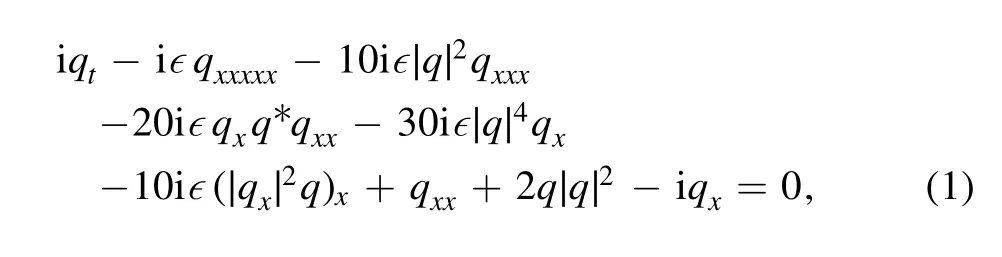
where q=q(x，t)represents the complex functions of x and t，∈is the perturbation parameter，and superscript‘*’means the complex conjugate.In 2015，Chen first constructed the generalized Darboux transformation(DT)of the inhomogeneous fifth-order NLS equation (1) and then obtained the RW solutions based on the generalized DT[45].In 2019，Feng et al studied the determinant representation of the N-fold DT based on Lax pair.Moreover，the higher-order solitary wave，breather wave and RW solutions in equation(1) are obtained by using the N-fold DT [46].In 2020，Yang et al discussed equation(1)with NZBCs in detail.For the inverse scattering problem，they discussed simple zeros and double zeros cases of scattering coefficients and further obtained their exact solutions [47].However，the BS solitons with zero boundary conditions(ZBCs)and the RW with nonzero boundary conditions (NZBCs) of equation (1) have not been analyzed.Therefore，we will use the RH problem to obtain the BS solitons of the inhomogeneous fifth-order NLS equation (1) with ZBCs.Then the RH problem of equation(1)with NZBCs is discussed.Finally，based on the obtained RH problem and the DT method，the RW solution of equation (1) with NZBCs is obtained.

Equation (1) satisfies the following Lax pair

where

with

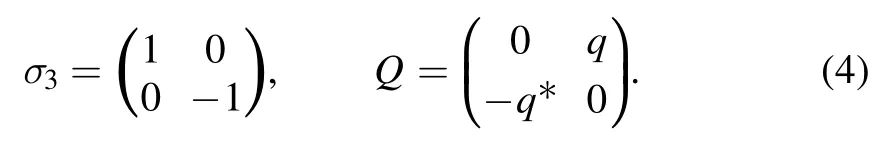
The structure of this paper is as follows:In section 2，we construct the RH problem of equation (1) with ZBCs，and then derive the BS soliton with a higher-order pole.In section 3，we construct the RH problem of the inhomogeneous fifth-order NLS equation(1)with NZBCs by means of the robust IST.Then the modified DT method is applied to solve the RH problem and obtain the exact breather wave and RW solutions of equation(1)with NZBCs.In the last section，we give some conclusions.

2.The lST with ZBCs and BS solution

We will study the BS soliton q(x，t) of the inhomogeneous fifth-order NLS equation (1) with ZBCs through infinity under the following conditions

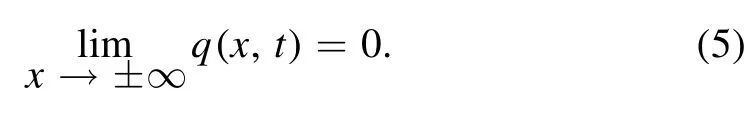
Next，we will express the IST and BS soliton of equation (1) with ZBCs through the research of the RH problem.

2.1.The structure of the RH problem with ZBCs

Let x →±∞，we rewrite the Lax pair (2) into the following form

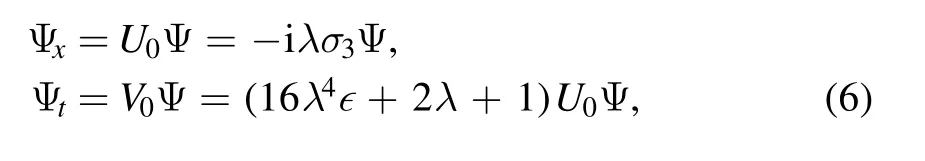
which satisfies the basic matrix solutionsand given by

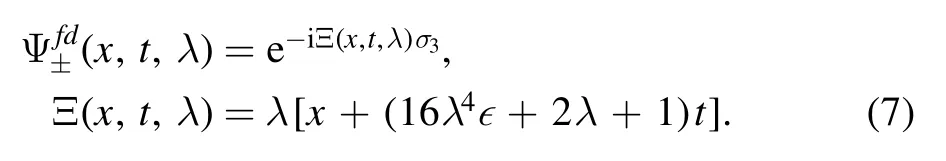
We get the Jost solutions Ψ±(x，t，λ)

Then，the modified Jost solutions μ±(x，t，λ)are expressed as

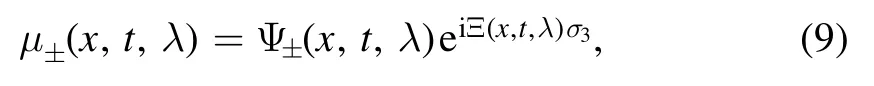
which fruit inμ±(x，t，λ) →I (x →±∞)，and satisfy the Volterra integral equations

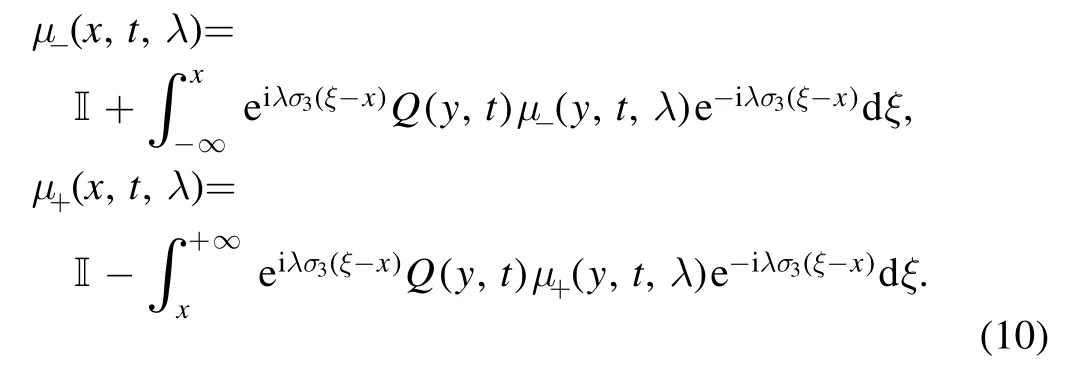
or

where μ±(x，t，λ) and S(λ) have the following symmetries

sjk(j，k=1，2) that can be shown as

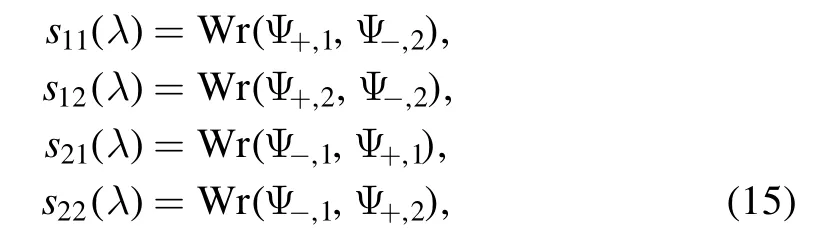
and s11is analytical for-C ，and s22is analytical forC+.In addition，s11，s22→1 (λ →±∞) in C-，C+，respectively.

Next，we will structure the RH problem.First，we need to consider the piecewise meromorphic matrices

Then，we obtain the following RH problem.

Theorem 1.M(x，t，λ)solve the following RH problem

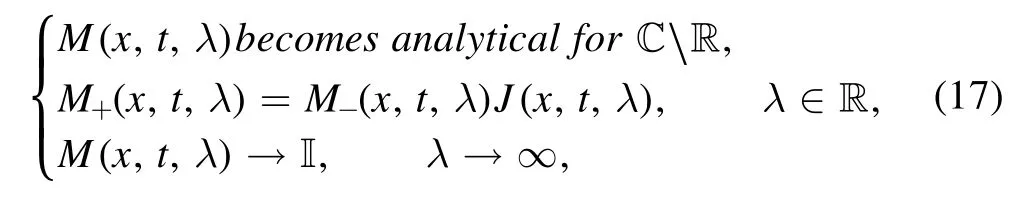
where the jump matrixJ(x，t，λ)is

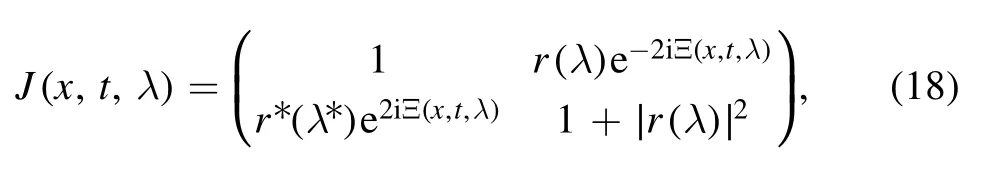
From equations (13) and (14)，we getM+(λ)=Letting

then q(x，t) of the inhomogeneous fifth-order NLS equation (1) with ZBCs is shown by the following formula

2.2.BS soliton with a higher-order pole

Generally，we assume that λ satisfying s22(λ)=0 in C+and λ*satisfying s11(λ*)=0 in-C (where λ and λ*are exactly discrete spectral points).Without thinking of simple poles，we suppose that s22(λ) has N higher-order poles λn，n=1，2，3，…，N in C+，which means

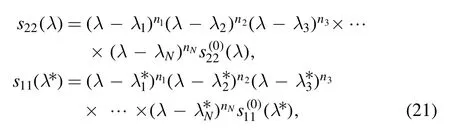
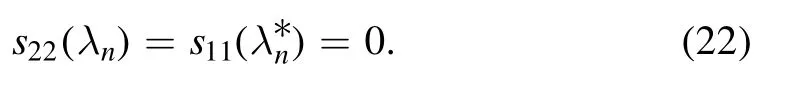
Therefore，the relevant λnandis represented as

and its distributions are given in figure 1.In the case of reflectionless potential(that is r(λ)=0)，we obtain the soliton solution of the inhomogeneous fifth-order NLS equation (1)with ZBCs.In this section，we will discuss the situation with an N-th order pole.This means that s22(λ) has an N-th order zero point on the upper half-plane (UHP) (that iss22(λ)=Similarly，we obtain that M11(x，t，λ) has an N-th order pole atλ=and M12(x，t，λ) has an N-th order pole at λ=λ0.Based on the normalization condition for M(x，t，λ)，we write the RH problem as follows

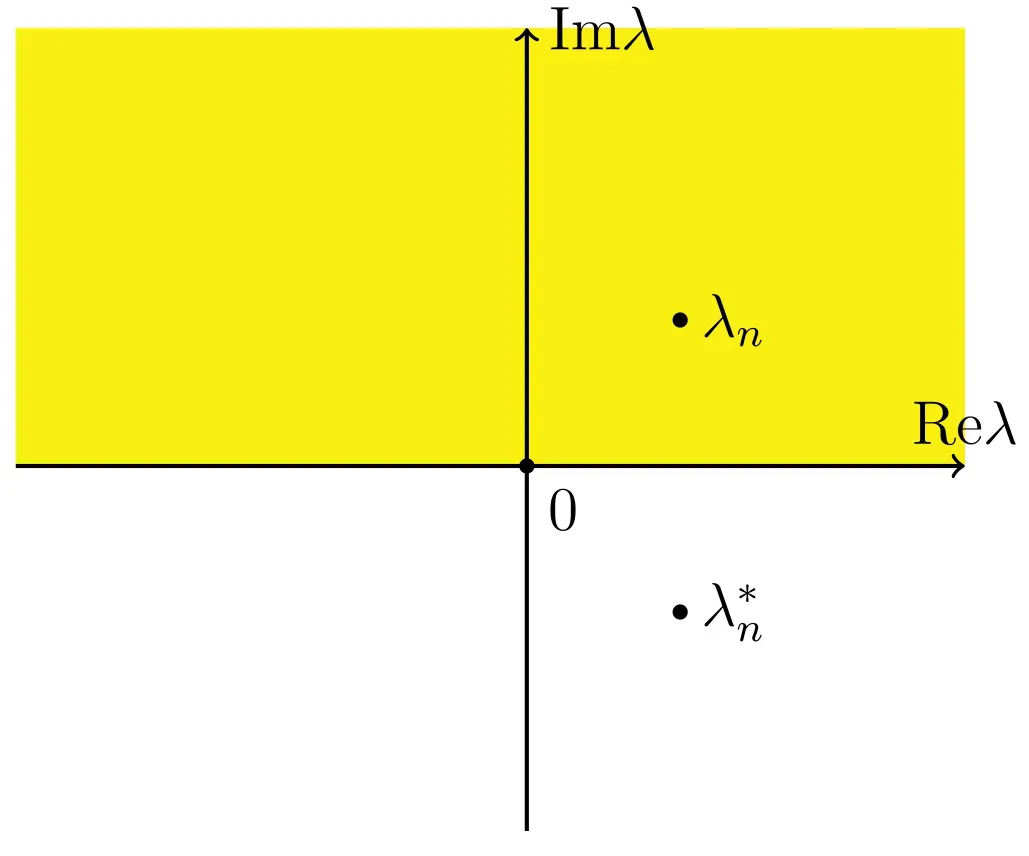
Figure 1.Depicts the contours and the discrete spectrum of the RH problem on complex λ-plane，C+ (yellow) and -C (white).

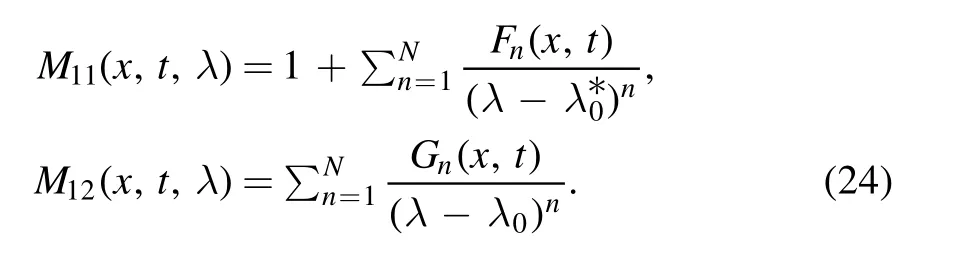
Simultaneously，defining

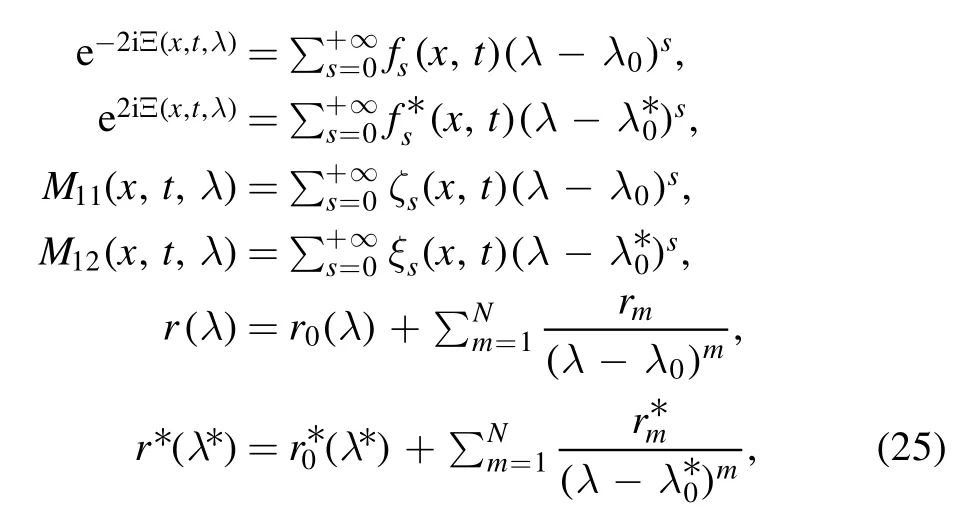
where

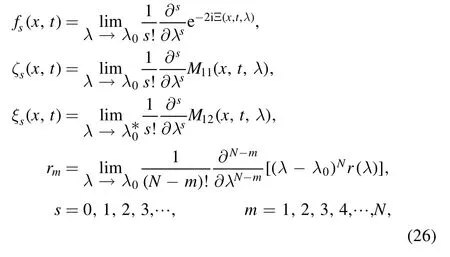
and r0(λ) means analytical for the UHP.

On the basis of the theorem 1，(24) and (25)，then we collect the correlation coefficients of(λ-λ0)-nandto get

with n=1，2，3，…，N.

Similarly，putting (24) into (26)，we have

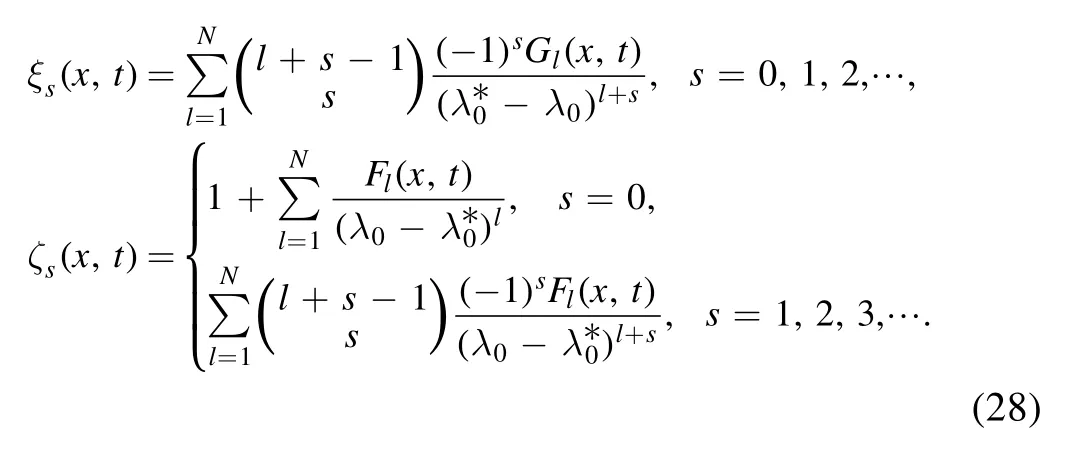
Putting (28) into (27)，we obtain

Subsequently，we can conclude the following theorem.

Theorem 2.Based on the ZBCs at infinity provided in(5)，the N-th order BS soliton of the inhomogeneous fifth-order NLS equation (1) is

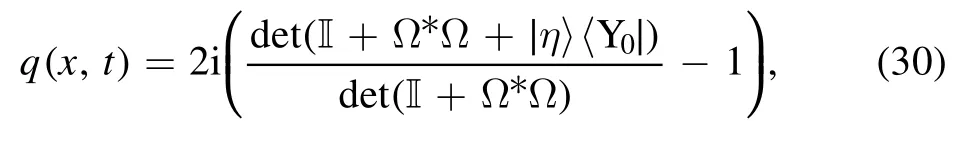
where〈Y0∣ = [1 ，0，0，… ，0]1×Nand

Proof.First，we introduce

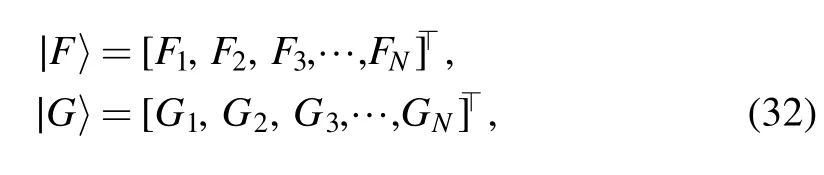
where the superscript”⊤”means transposition.Subsequently，we can transform equations (29) into the following form

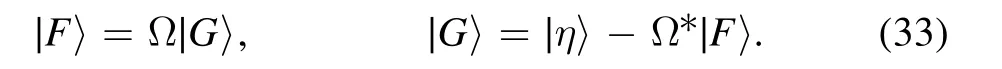
Then，we obtain

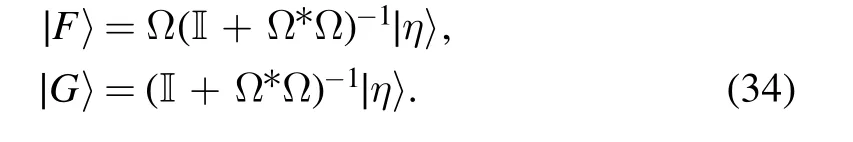
Putting (34) into (24)，we have

When N=2，λ=λ0is the second-order zero point of s22，then r(λ) is rewritten as follows

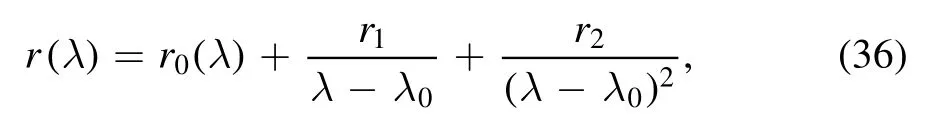
and Ω11，Ω12，Ω21and Ω22are expressed as

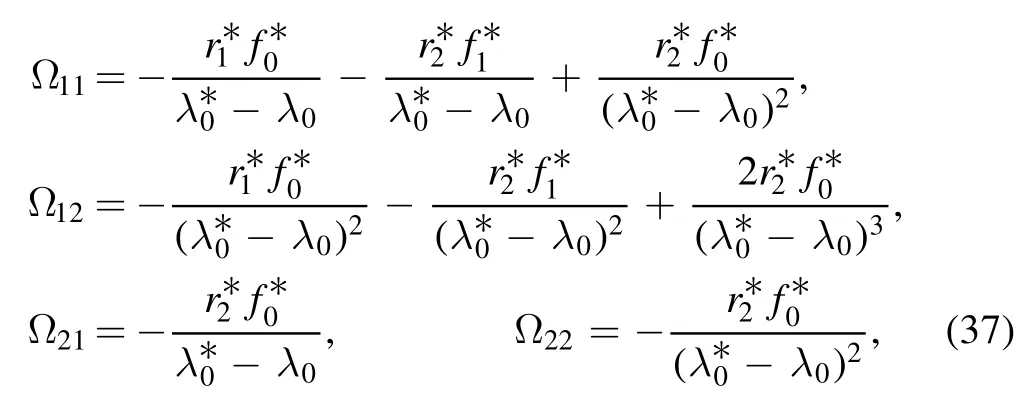
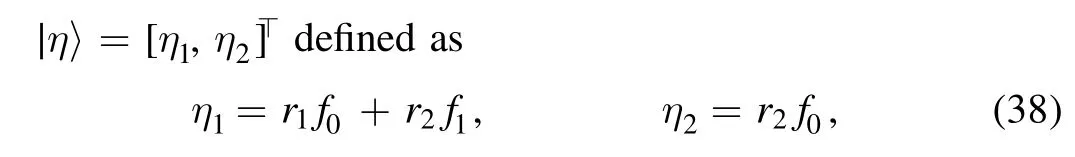
and〈Y0|=[1，0].Furthermore，on the basis of the theorem 2，let r1=r2=1，λ0=a+bi，we obtain that the second-order BS soliton solution of the inhomogeneous fifth-order NLS equation (1) is

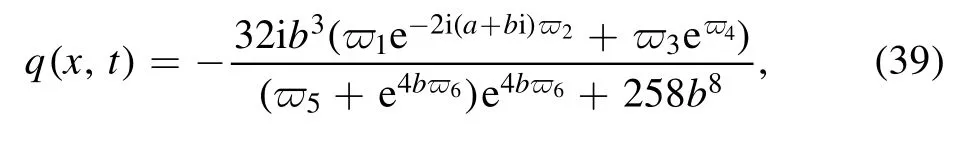
where

The BS soliton solution (39) means the interaction between two soliton solutions，in which the high peak is caused by the interaction of two solitons with related eigenvalues.The relevant evolution process for the solutions (39)at different coefficient ∈are counseled in Figure 2.We can find that the change of parameter ∈affects the phase for the two solitons in Figure 2.

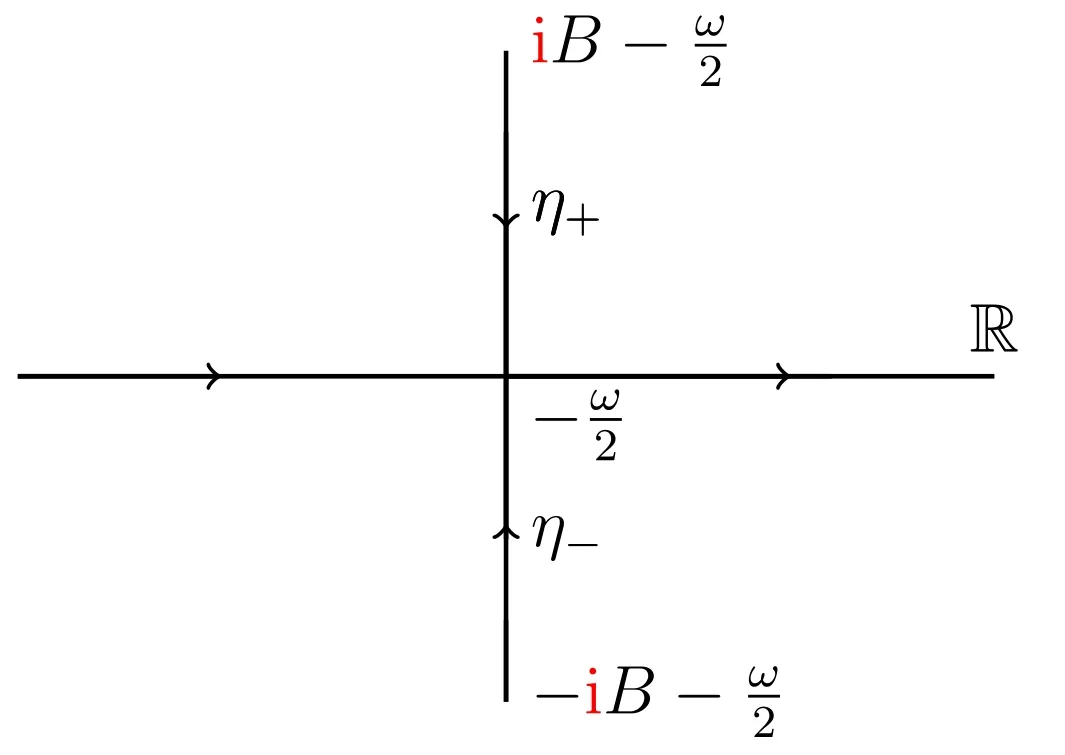
Figure 3.The contour Σ 0 = R ∪ηof the basic RH problem.

3.The lST with NZBCs and RW

We will study the RW solution q(x，t) of the inhomogeneous fifth-order NLS equation (1) with NZBCs through infinity under the following conditions

where ω and B ＞0 expressions real constants，ν=(30B4ω −20B2ω3+ω5)∈+2B2−ω2+ω.

3.1.The structure of the RH problem with NZBCs

where

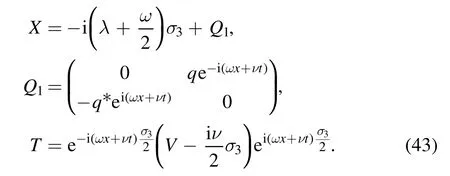
By the NZBCs (41)，we can rewrite the above Lax pair(42) into the following form

where

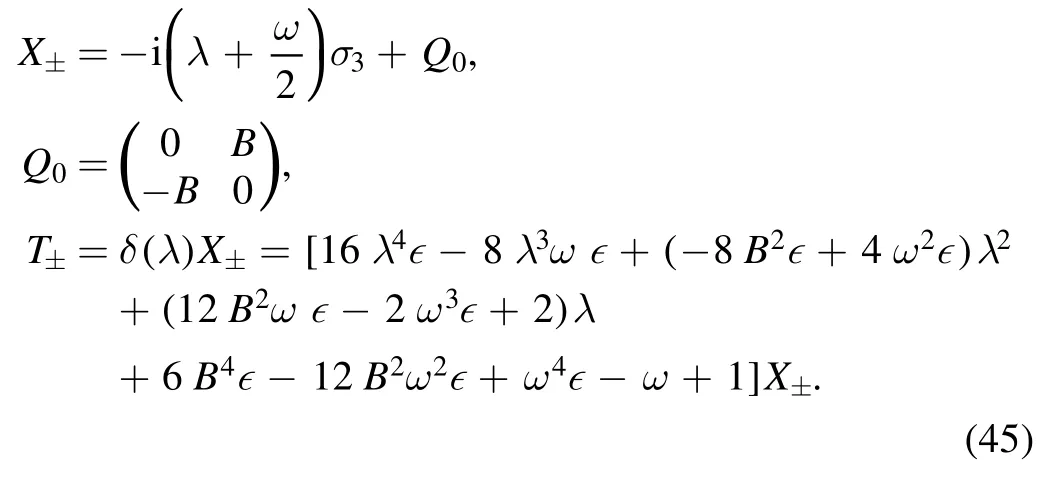
According to the Lax pair (44)，we can get the following solution

where

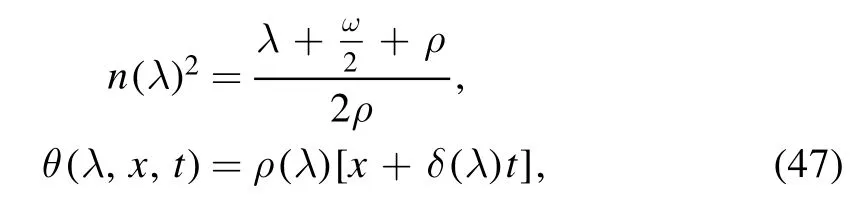
We assume that Φ±(λ，x，t) are also the solution of the Lax pair(44)and Φ±(λ，x，t)→ψ±(λ，x，t)(x →±∞).Then，taking transformation

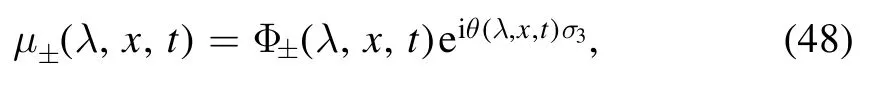
with

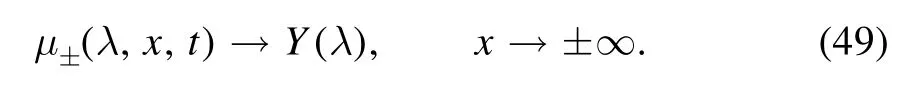
Then we can immediately calculate that μ±satisfy

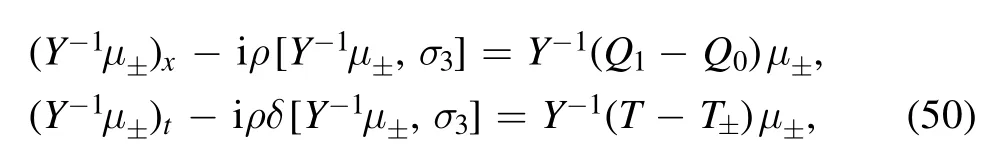
and satisfy the following Volterra integral equations

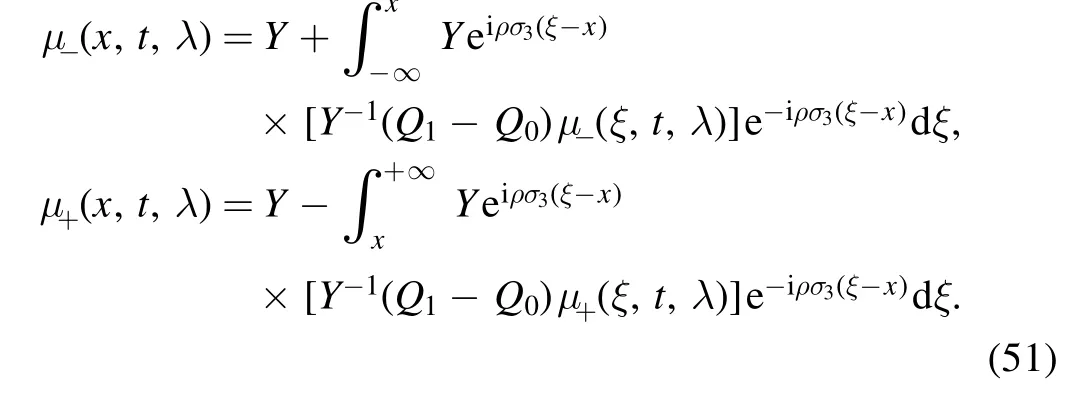
the scattering matrix is shown as

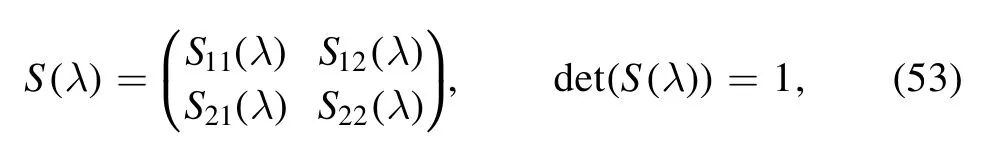
where the jump matrixJ(x，t，λ)is

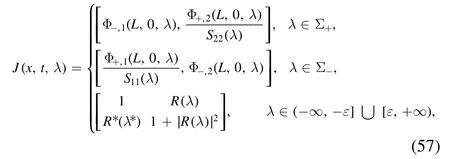
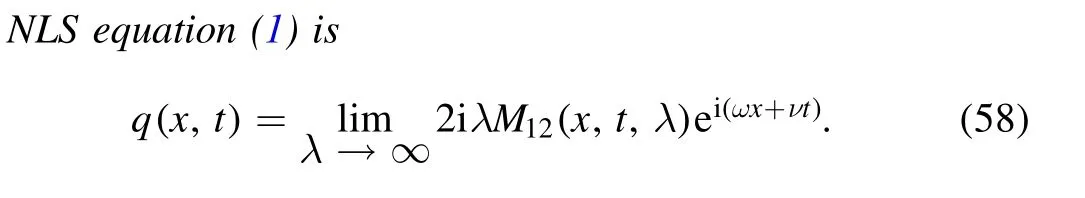
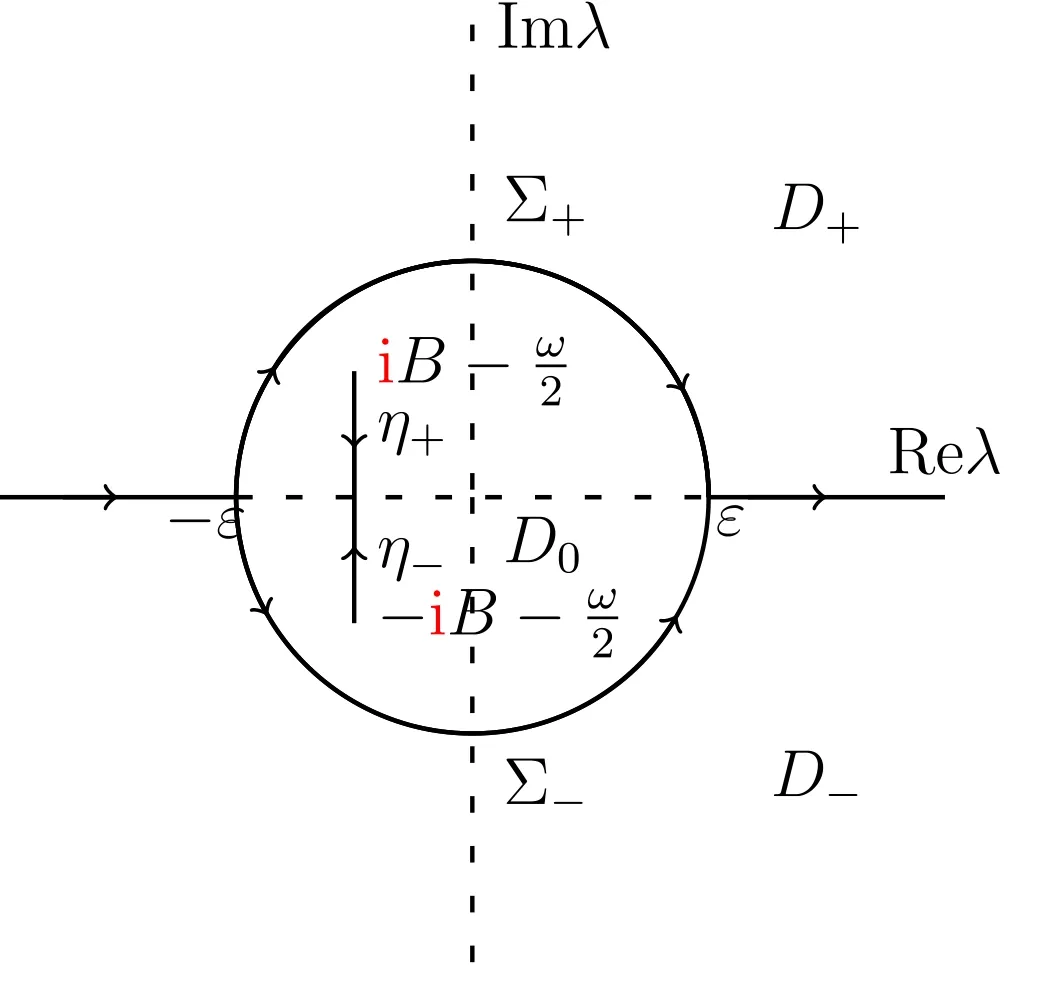
Figure 4.Definitions of the regions D±，D0 and Σ±，η.

3.2.RW of the inhomogeneous fifth-order NLS equation

We will use the modified DT for theorem 1 to obtain the higher-order RW of the inhomogeneous fifth-order NLS equation (1).We make the following specification transformation

where φ(x，t，λ) satisfies the above Lax pair (42) andφ(L，0，λ) =I (λ ∈D0).The T is expressed as

for ∀λ ∈D0where H(x，t) and Y(x，t) can be written as

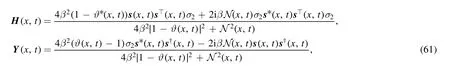
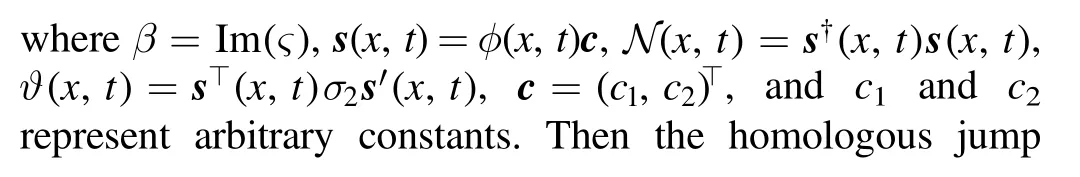
Furthermore，we get

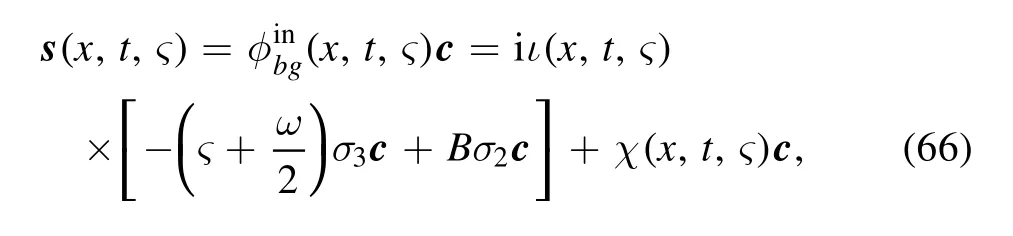
where

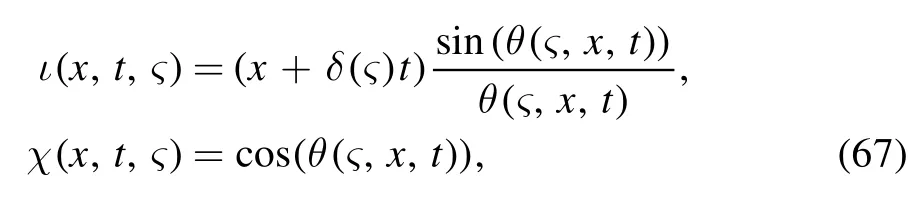
and

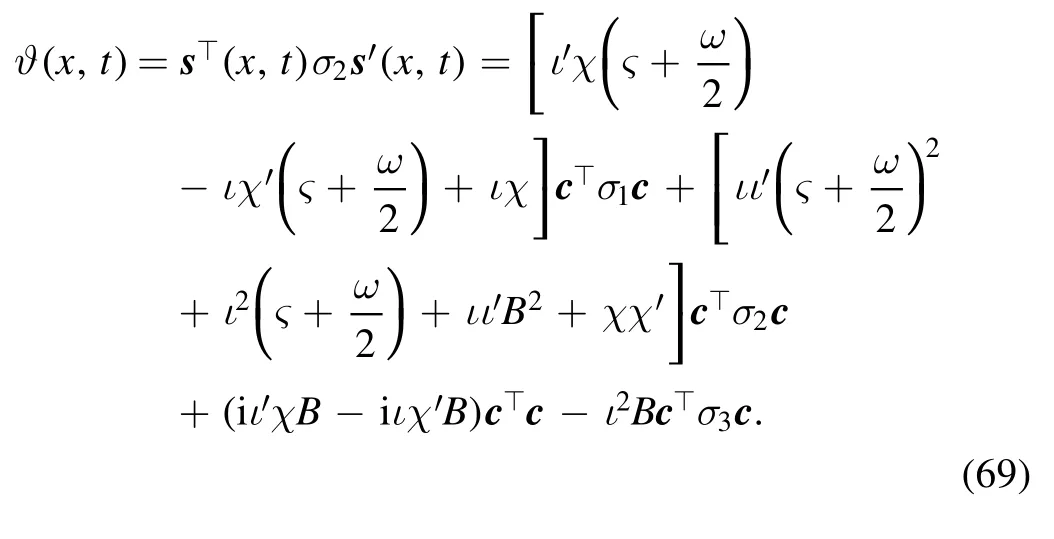
Therefore，the solutions of equation (1) are

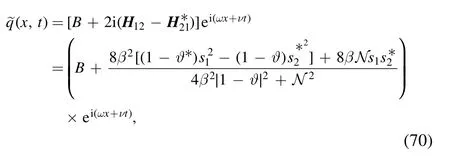
wheres= (s1，s2)⊤，N and ϑ are provided in expres sions(66)，(68) and (69).Furthermore，letting c=c∞ε−1with ε →0，the solution (70) can be rewritten as follows

where s∞，∞N and ϑ∞are provided in expressions(66)，(68)and (69) with c replaced by c∞，respectively.

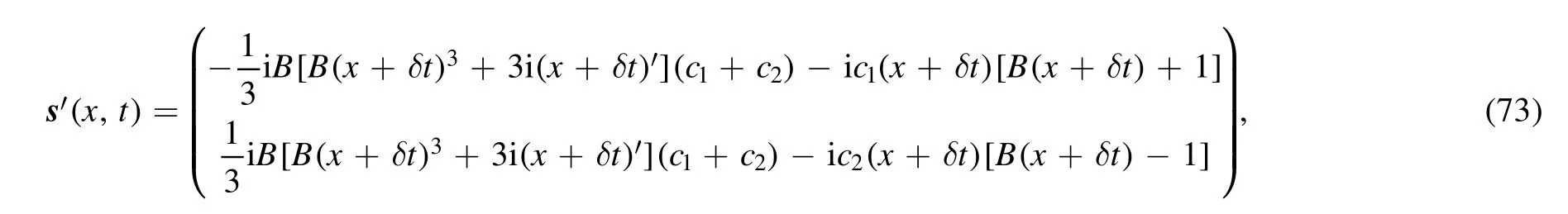
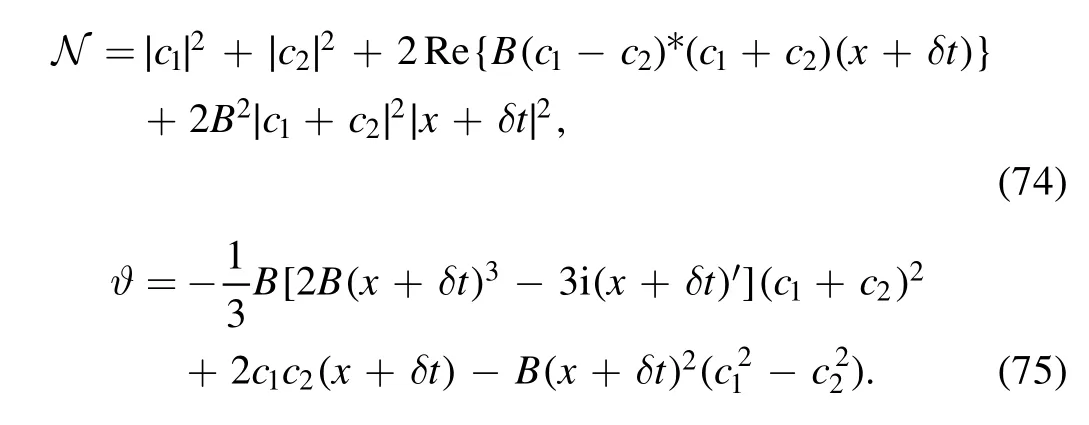
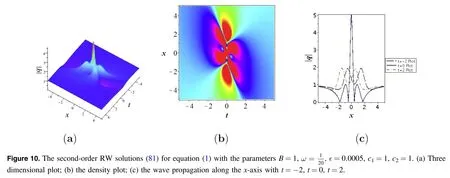
Then we can find that the first-order RW can be deduced at c1+c2=0.

(a) For c1=−c2=1，we obtain the first-order RW solution as (see figure 7)

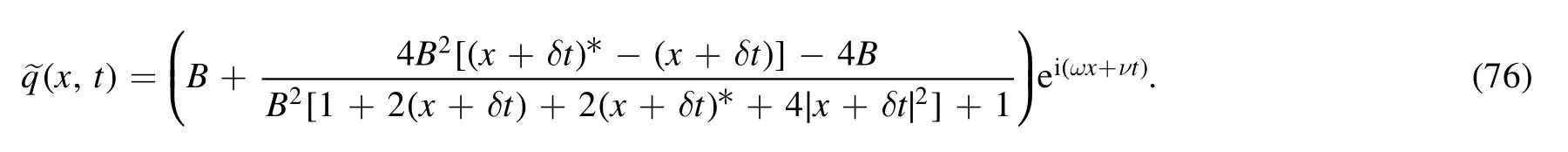
where

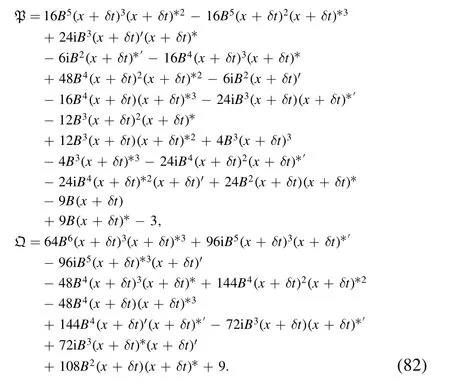
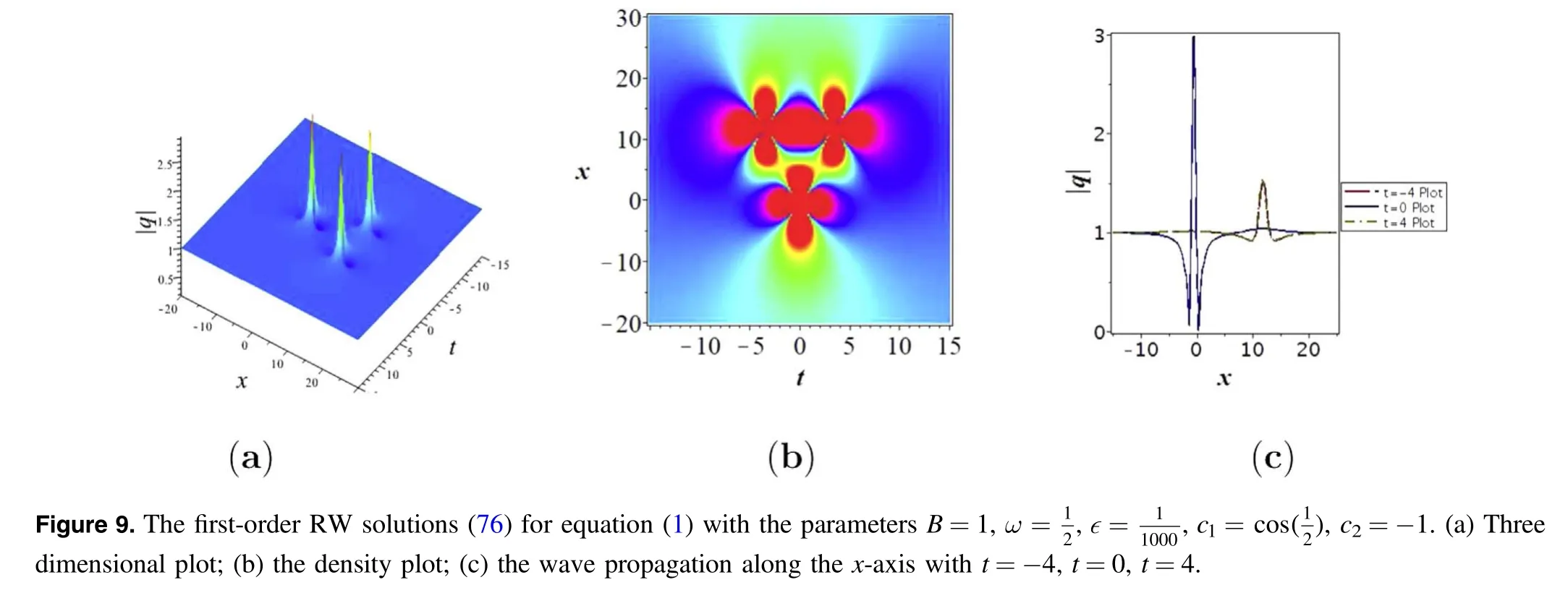
4.Conclusions

The present work studied the BS soliton and RW solutions of the inhomogeneous fifth-order NLS equation (1) with ZBCs and NZBCs by the RH method.In this context，the RH problem of equation (1)is constructed，and an N-th order BS solitons of equation(1)with ZBCs are obtained by the residue theorem and Laurent’s series.Also，some dynamic behaviors of the second-order BS soliton solutions are analyzed for equation (1) in the form of images.It is manifested that parameters can change the shape and size of the two soliton waves (figure 2).In the meantime，the RH problem of equation (1) with NZBCs is constructed by robust IST.Then the RW solutions of equation (1) are obtained via the modified DT.The graphs of the temporal-spatial periodic breather waves and the spatial periodic breather waves are drawn，which revealed that parameter ς had a certain influence on the breather wave solutions (figure 5 and figure 6).Finally，the first-order and the second-order RW are obtained by modulating parameters in equation (1).

Although the exact solutions of equation(1)with NZBCs are derived in [47]，the RW solutions of equation are studied by DT in [46].However，in this paper，we mainly study the BS solitons with ZBCs and the RW solutions with NZBCs of equation (1)，the obtained solutions are of more extensive significance and richer content.In addition，the proposed method in this paper can be further extended to identify some other nonlinear systems，and the method can be optimized to improve the results in the future.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant No.11975306，the Natural Science Foundation of Jiangsu Province under Grant No.BK20181351，the Six Talent Peaks Project in Jiangsu Province under Grant No.JY-059，and the Fundamental Research Fund for the Central Universities under the Grant Nos.2019ZDPY07 and 2019QNA35.